Figures (15)  Tables (4)

    • Figure 1. 

      Common gyroidal roads in China. (a) Longmen ancient road at the junction of Henan and Shanxi; (b) East line mountain road project in Fugu County, Yulin City, Shaanxi Province.

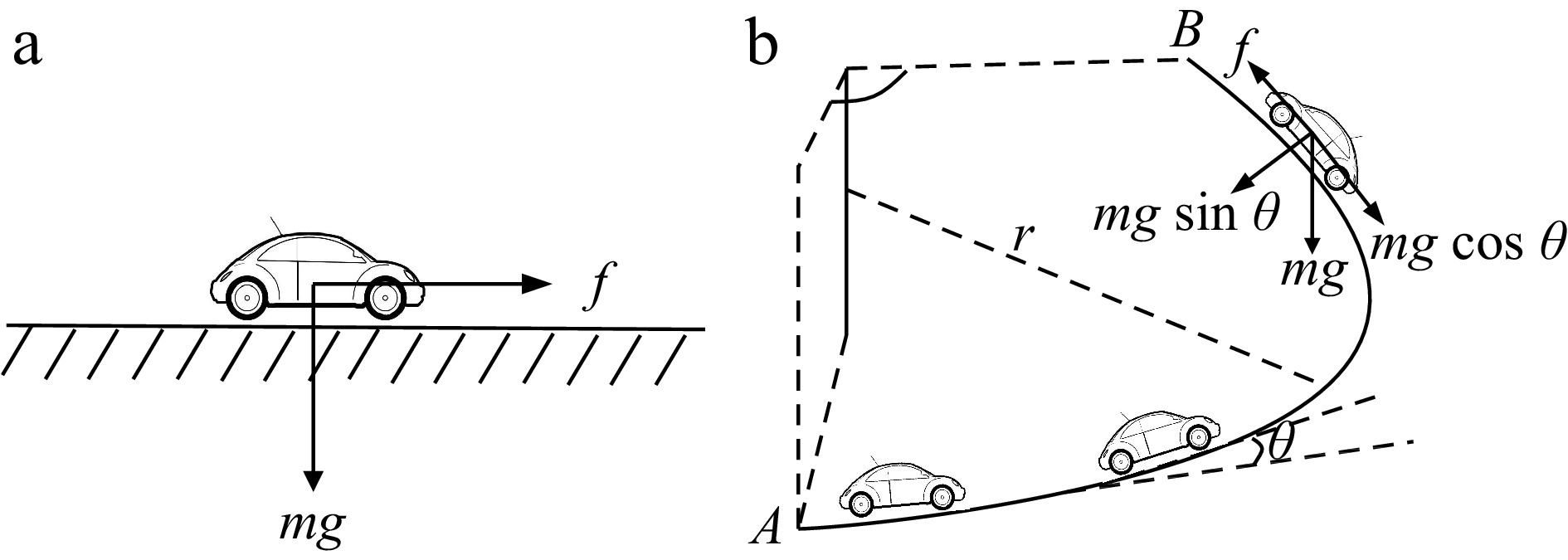
    • Figure 2. 

      Illustration of vehicle forces on different road scenes, (a) horizontal or regular road, (b) gyroidal road.

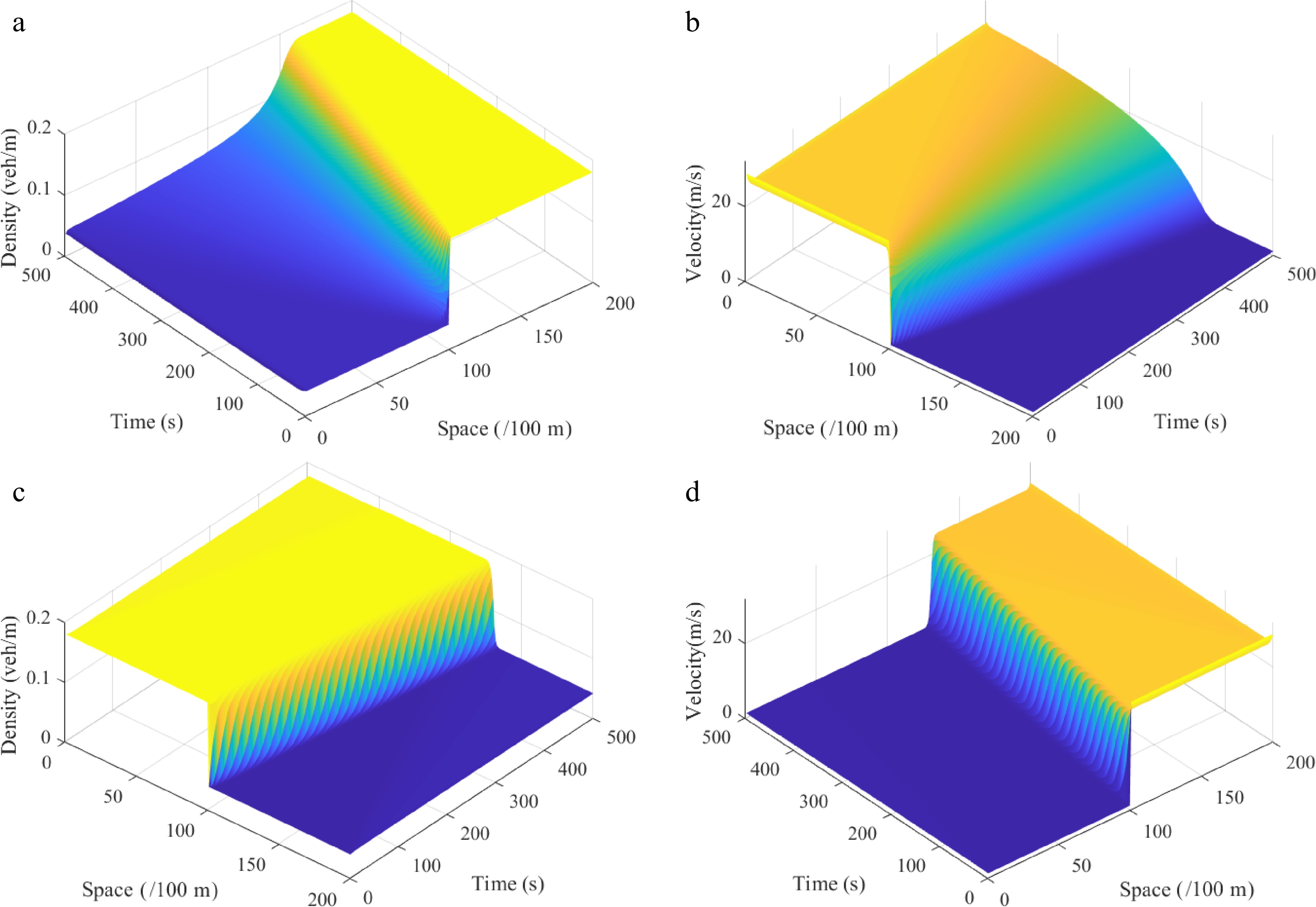
    • Figure 3. 

      Shock waves under the Riemann initial condition (i), where: (a) density $ \rho (\varphi ,t) $; (b) velocity $ \omega r $; the rarefaction waves under the Riemann initial condition (ii), where: (c) density $ \rho (\varphi ,t) $; (d) velocity $ \omega r $. (Under downhill scenes) ($ \theta {\text{ = }} $ = −6).

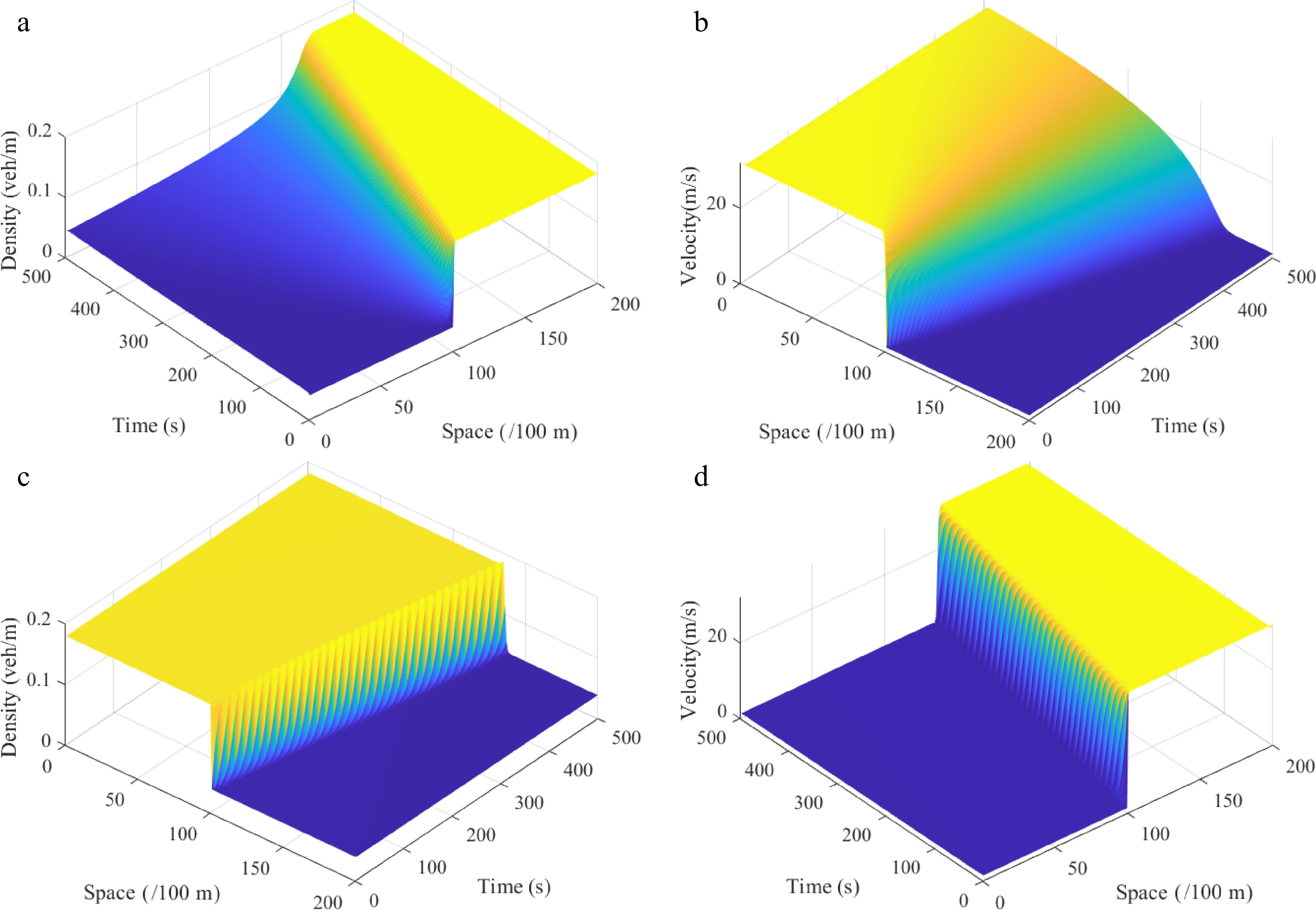
    • Figure 4. 

      Shock waves under the Riemann initial condition (i), where: (a) density $ \rho (\varphi ,t) $; (b) velocity $ \omega r $; the rarefaction waves under the Riemann initial condition (ii), where: (c) density $ \rho (\varphi ,t) $; (d) velocity $ \omega r $. (Under uphill scenes) ($\theta$ = 6).

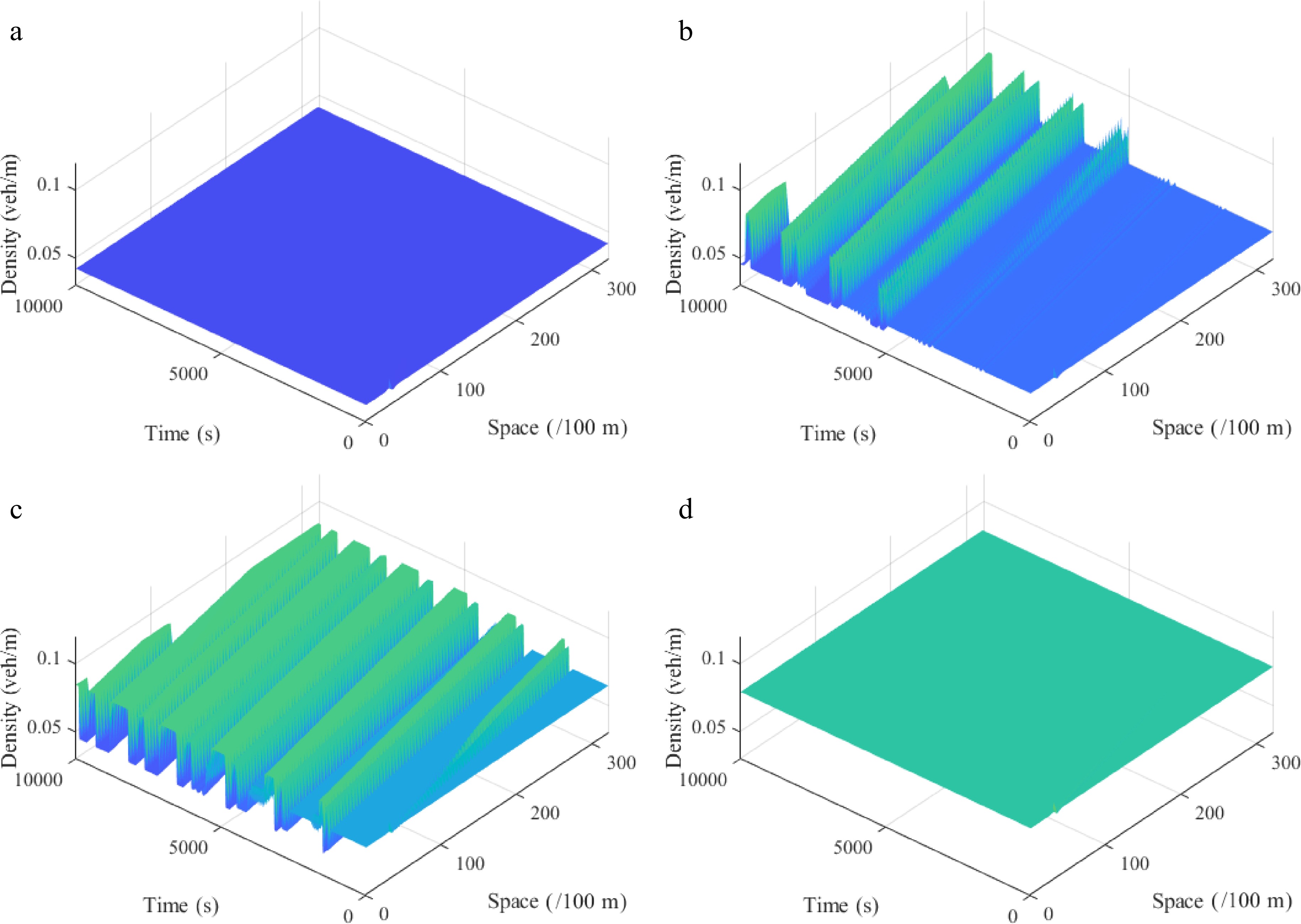
    • Figure 5. 

      Spatiotemporal diagram of density waves affected by the initial disturbance under different initial densities ρ0, where: (a) ρ0 = 0.042 veh/m; (b) ρ0 = 0.051 veh/m; (c) ρ0 = 0.065 veh/m; (d) ρ0 = 0.079 veh/m. (l = 2, θ = 0, r = 75).

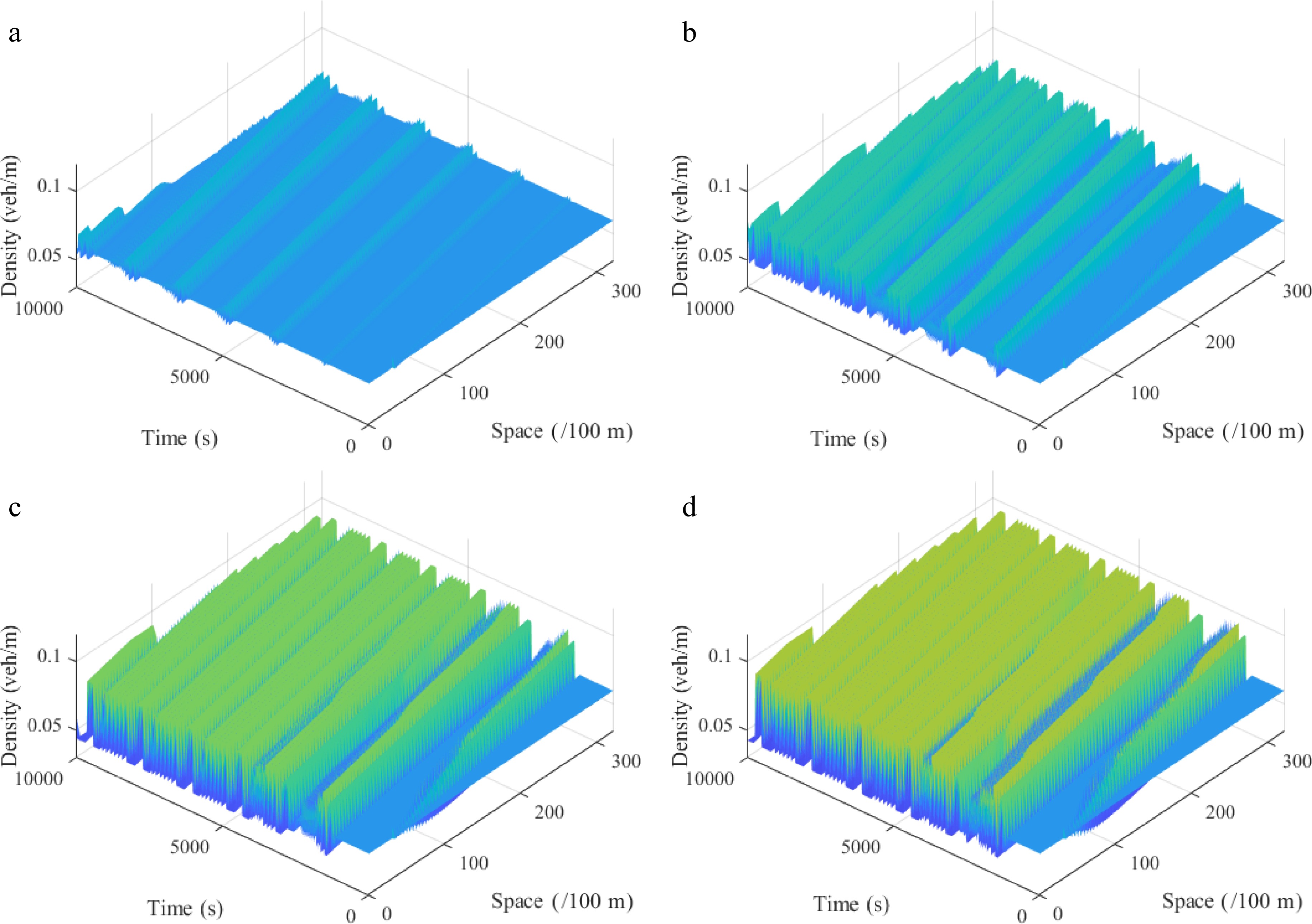
    • Figure 6. 

      Spatiotemporal diagram of density waves affected by the initial disturbance under different slope angles θ, where: (a) θ = −10; (b) θ = −5; (c) θ = 5; (d) θ = 10. (l = 2, ρ0 = 0.06, r = 75).

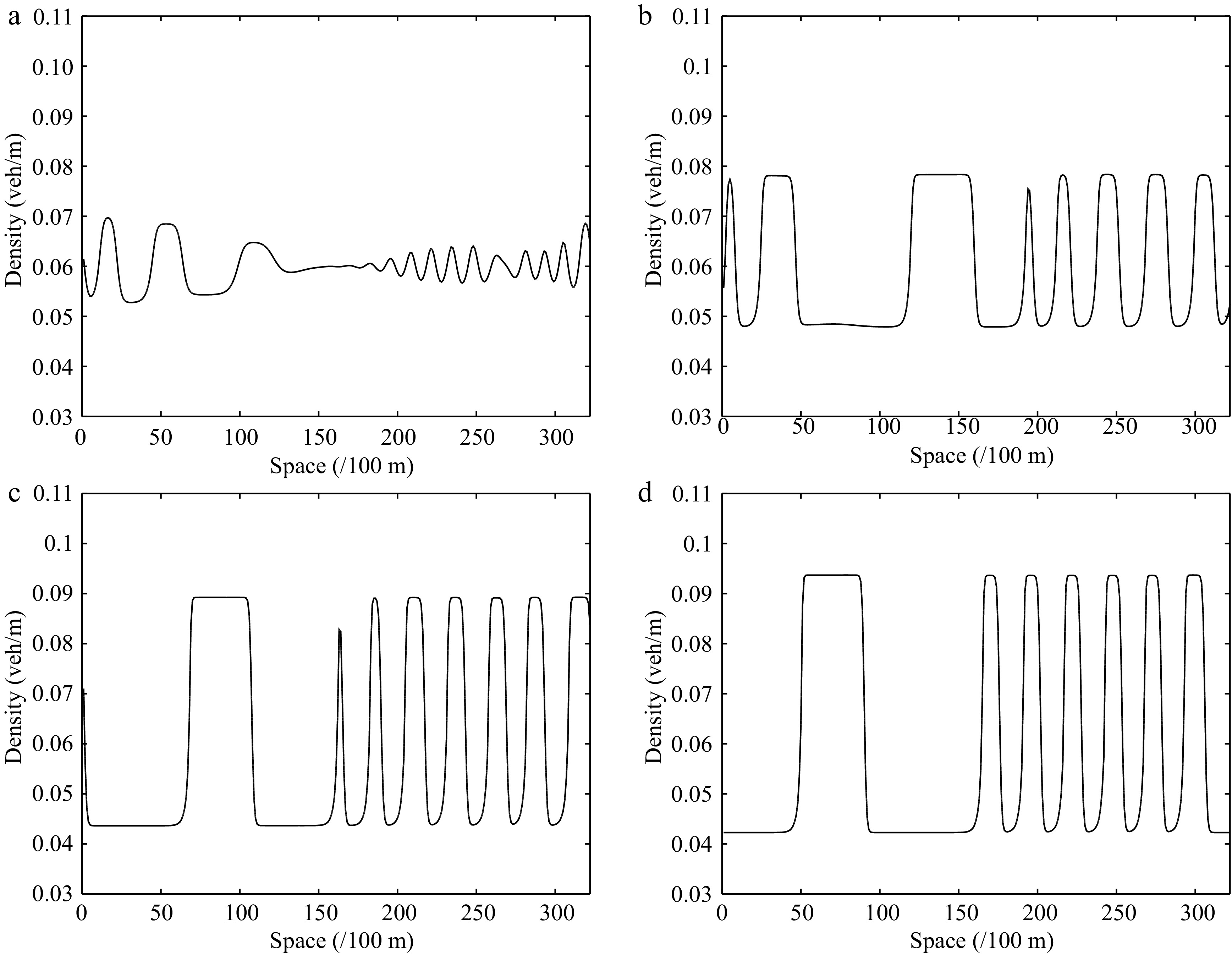
    • Figure 7. 

      Instantaneous density distribution of traffic flow corresponding to Fig. 6 at t = 3,000 s.

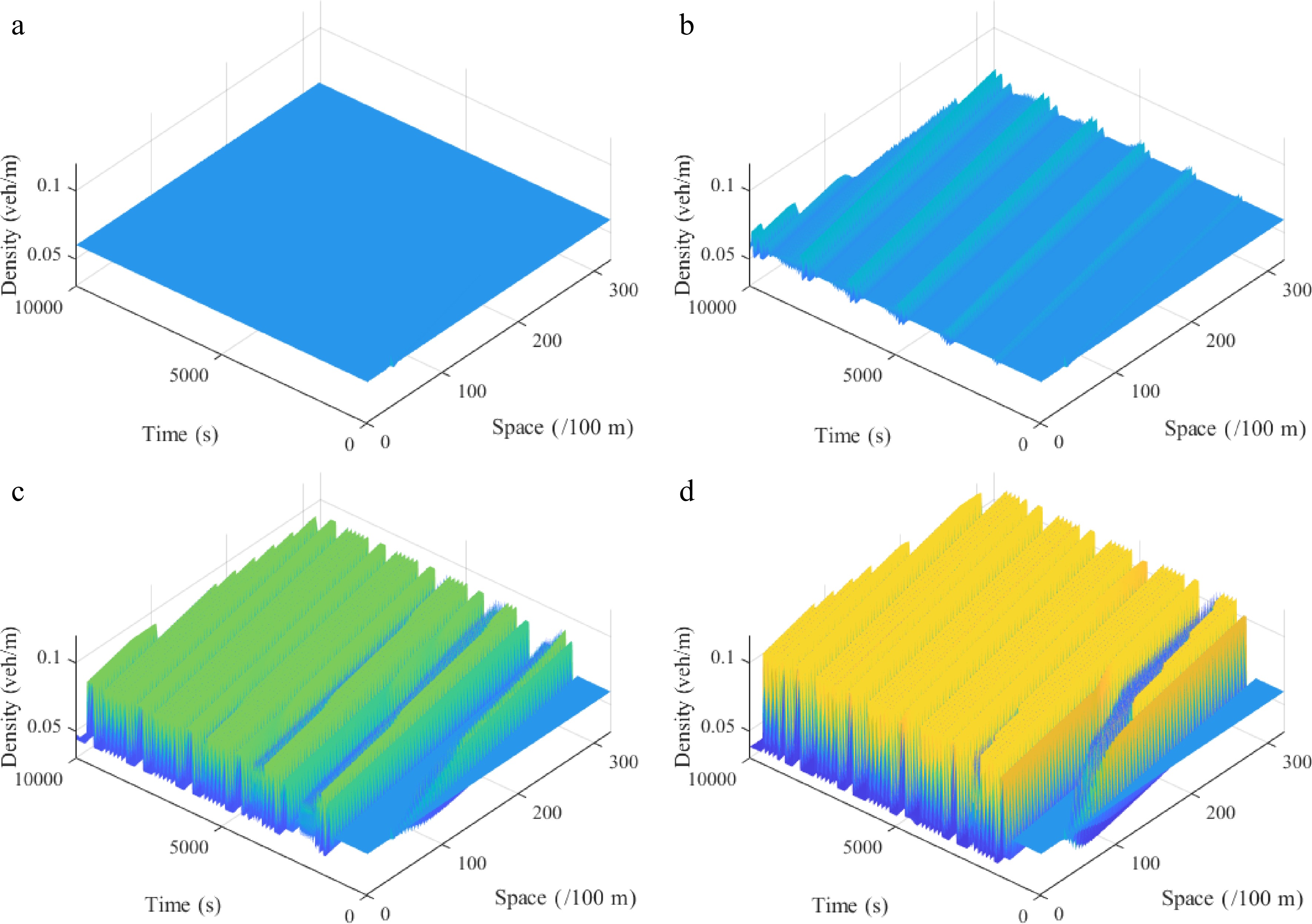
    • Figure 8. 

      Spatiotemporal diagram of density waves affected by the initial disturbance corresponding to different curvature radiuses r under the downhill scenario, where: (a) r = 50; (b) r = 70; (c) r = 90; (d) r = 120. ($ {\rho _0} $ = 0.06, $ \theta $ = −6, $ l $ = 2).

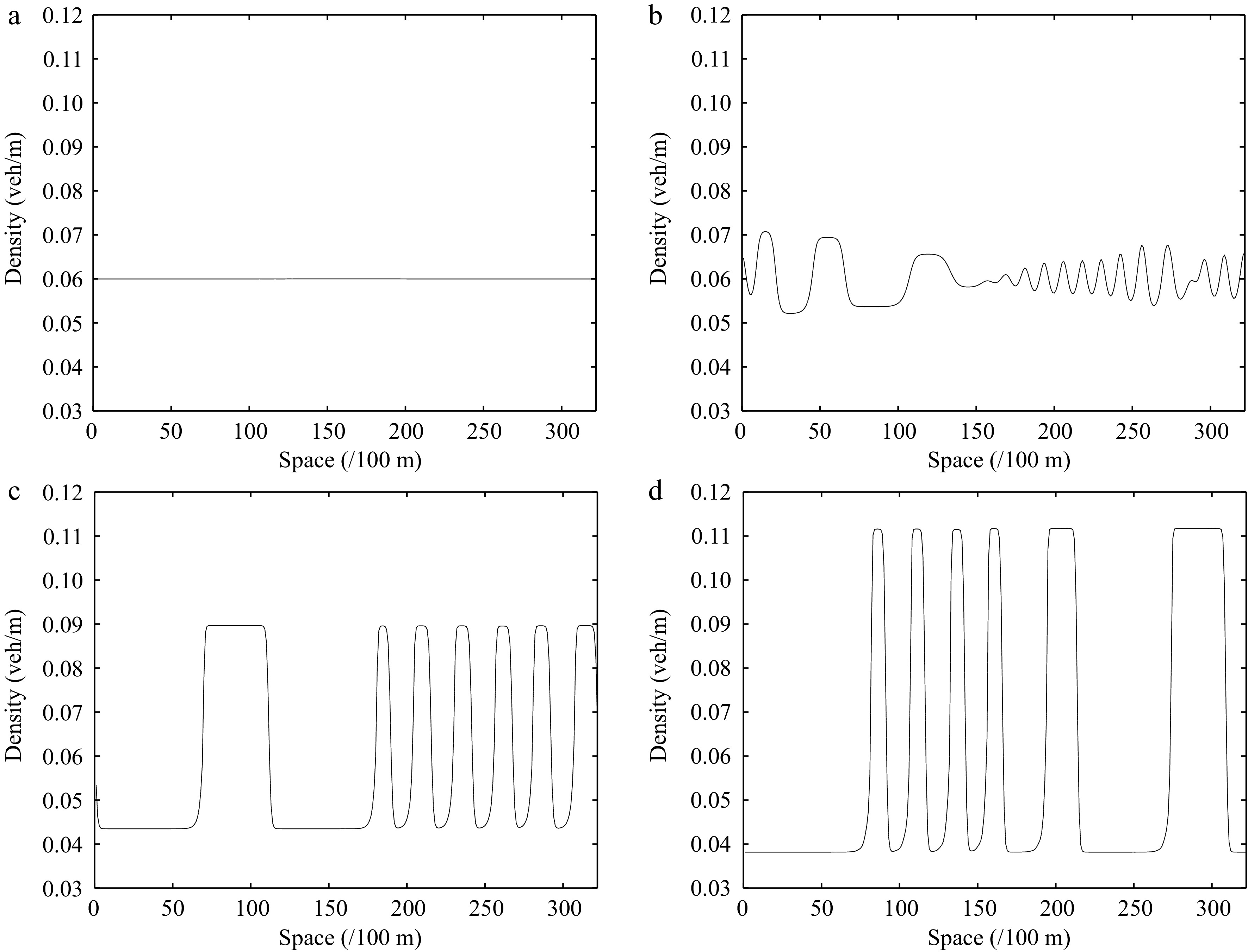
    • Figure 9. 

      Instantaneous density distribution of road traffic flow corresponding to Fig. 8 at t = 3,000 s.

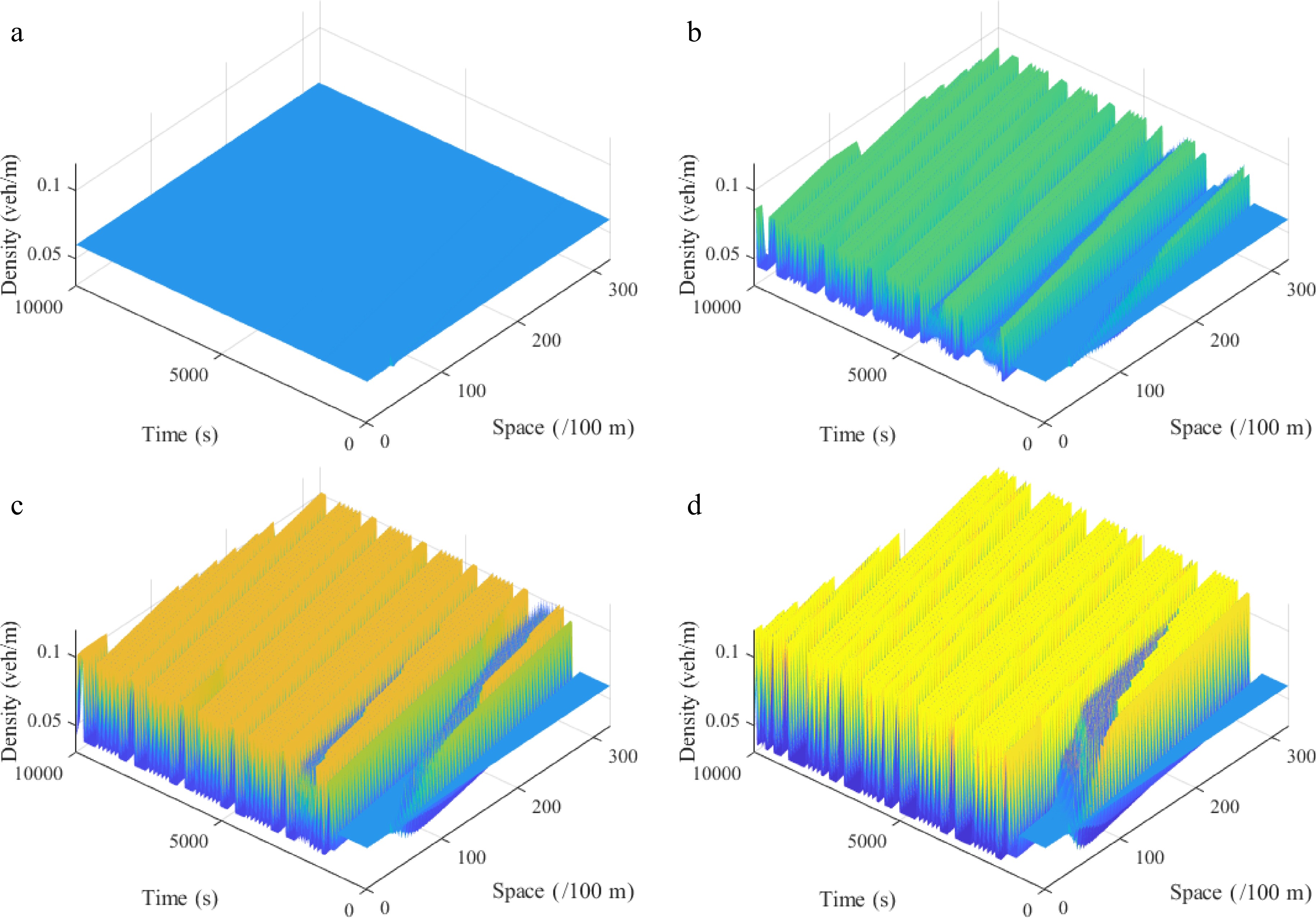
    • Figure 10. 

      Spatiotemporal diagram of density waves affected by the initial disturbance corresponding to different curvature radiuses r under the uphill scenario, where: (a) r = 50; (b) r = 70; (c) r = 90; (d) r = 120. ($ {\rho _0} $ = 0.06, $ \theta $ = 6, $ l $ = 2).

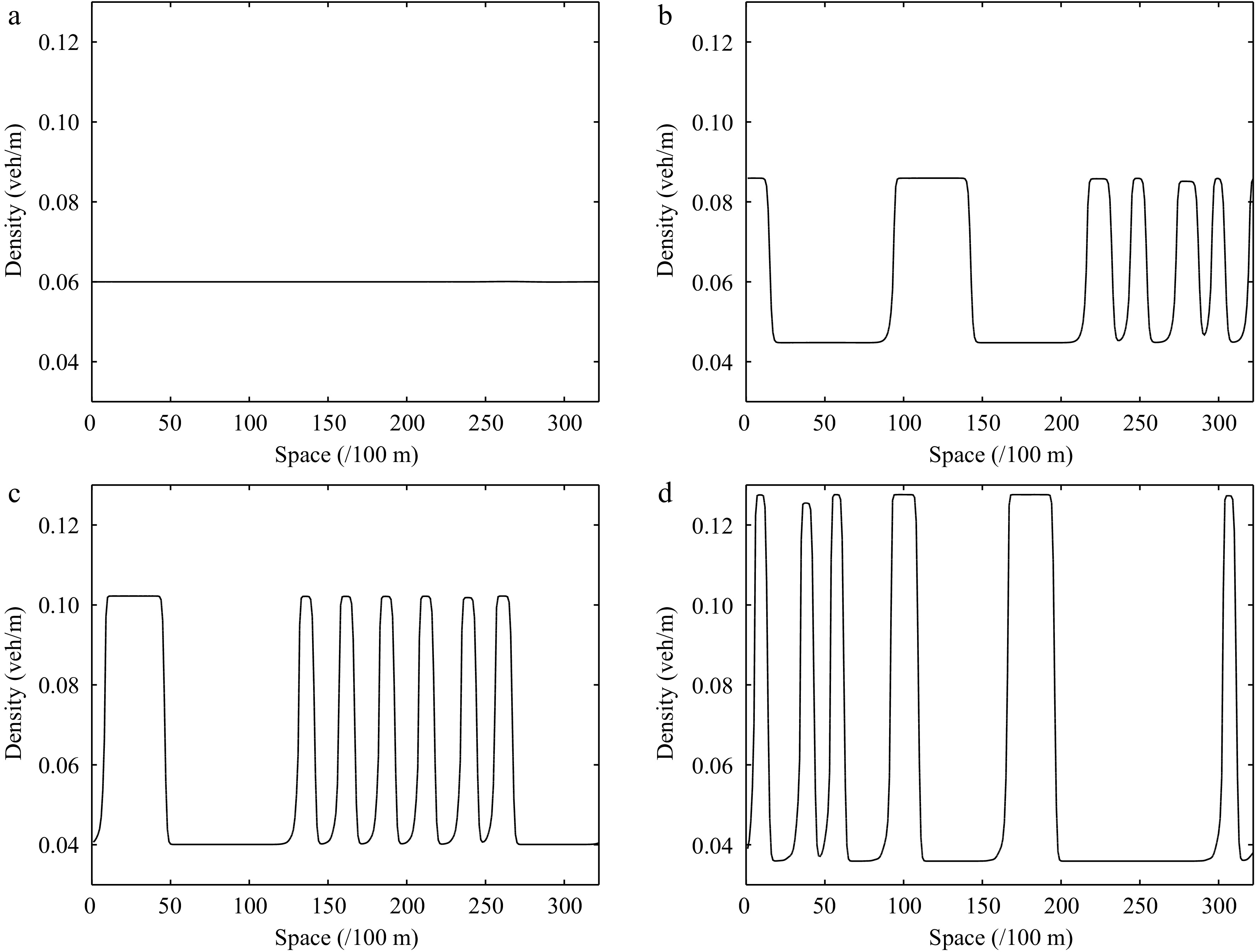
    • Figure 11. 

      Instantaneous density distribution of road traffic flow corresponding to Fig. 10 at t = 3,000 s.

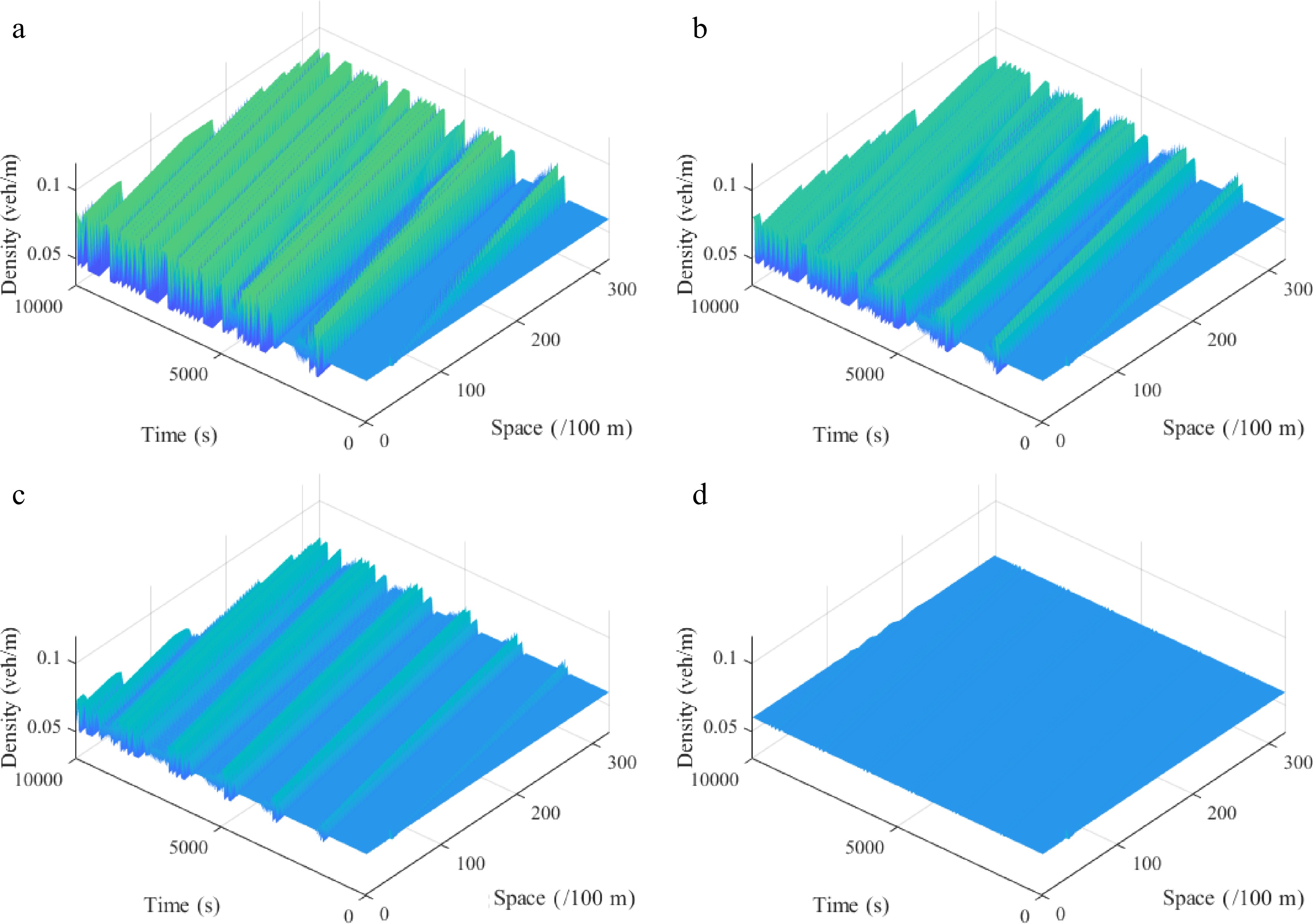
    • Figure 12. 

      Spatiotemporal diagram of density waves affected by the initial disturbance corresponding to different values of parameter l under a downhill scenario, where: (a) l = 0; (b) l = 1; (c) l = 2; (d) l = 3. ($ {\rho _0} $ = 0.06, $ \theta $ = −8, $ r $ = 75).

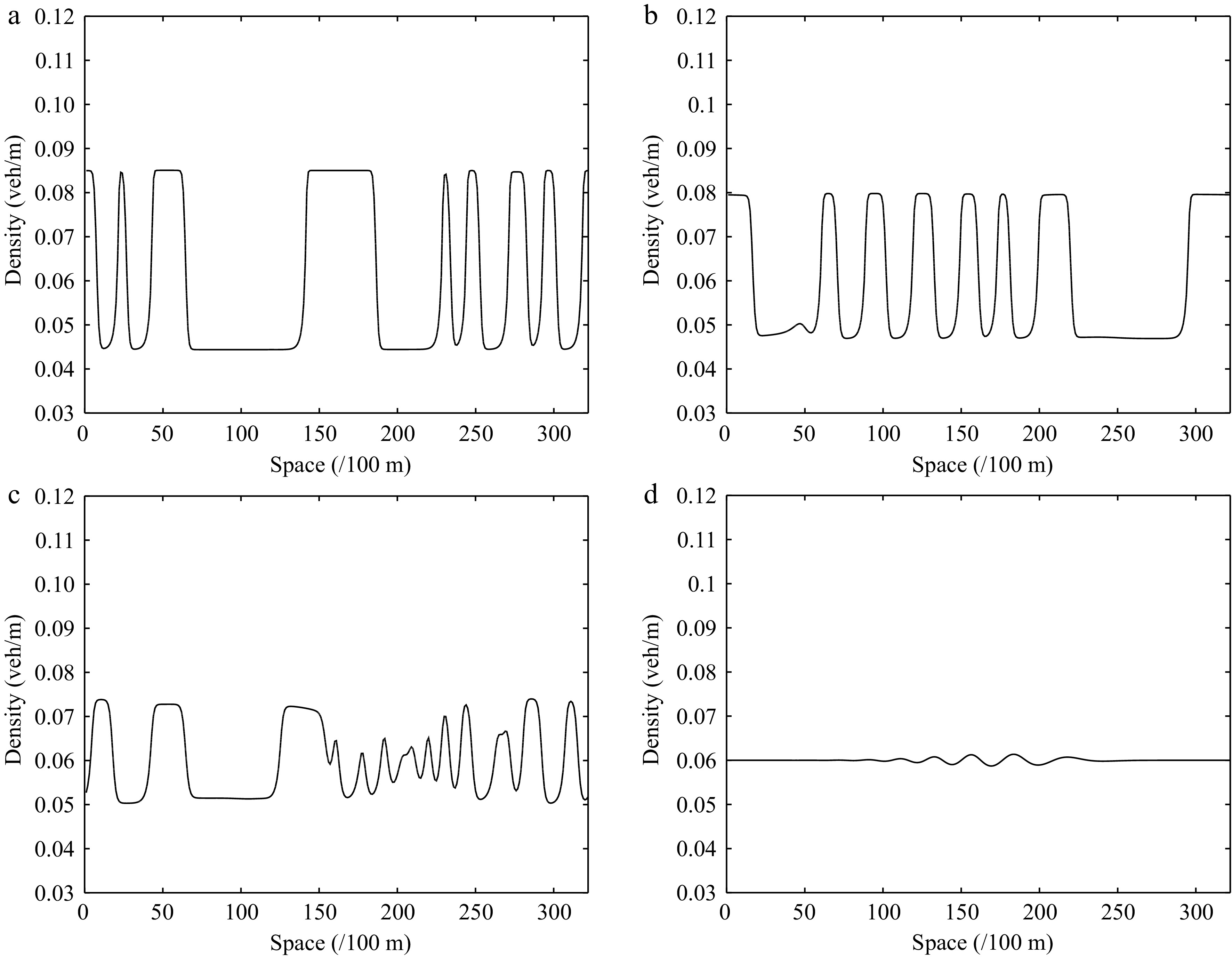
    • Figure 13. 

      Instantaneous density distribution of traffic flow corresponding to Fig. 12 at t = 3,000 s.

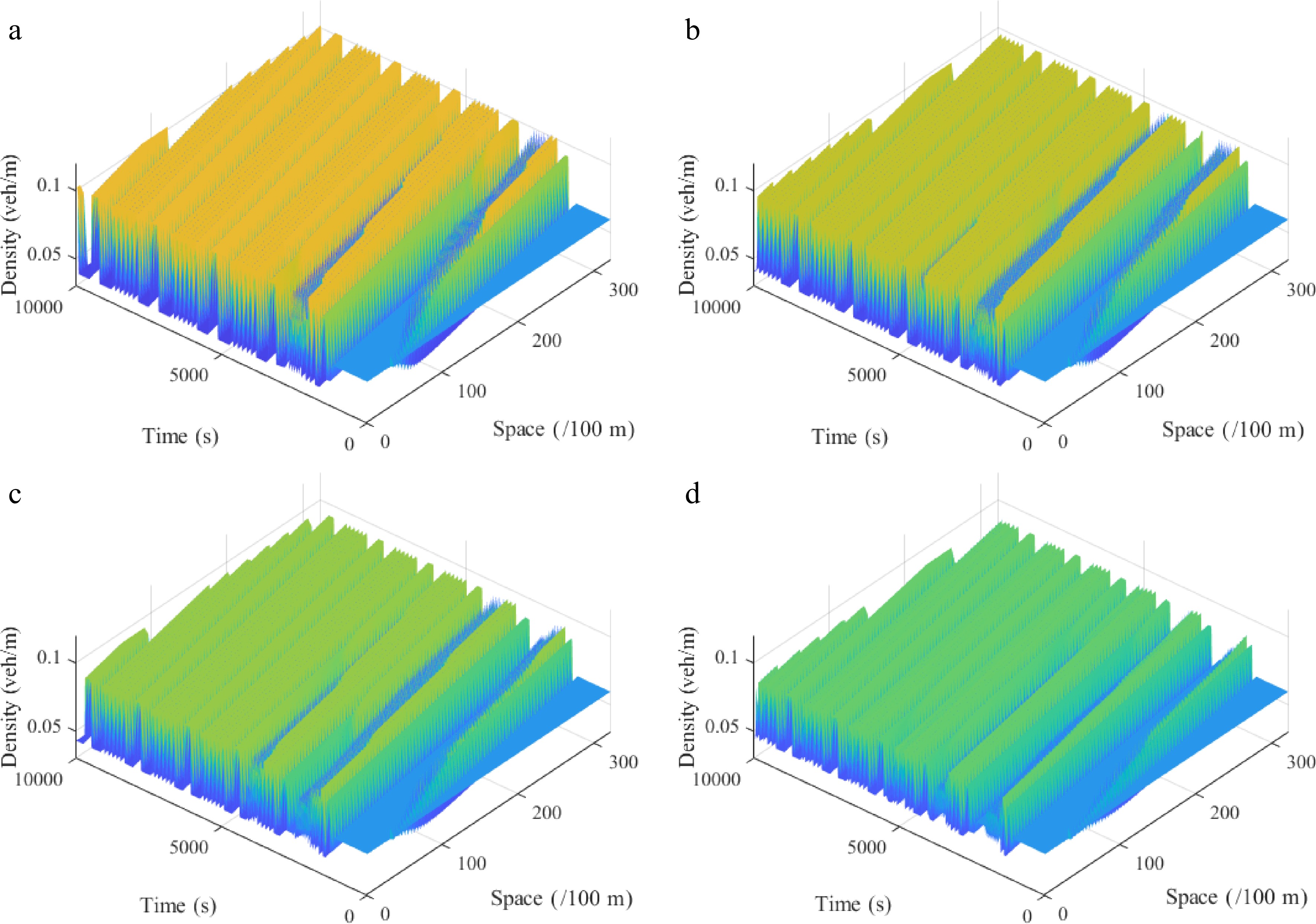
    • Figure 14. 

      Spatiotemporal diagram of density waves affected by the initial disturbance corresponding to different values of parameter l under the uphill scenario, where: (a) l = 0; (b) l = 1; (c) l = 2; (d) l = 3. ($ {\rho _0} $ = 0.06, $ \theta $ = 8, $ r $ = 75).

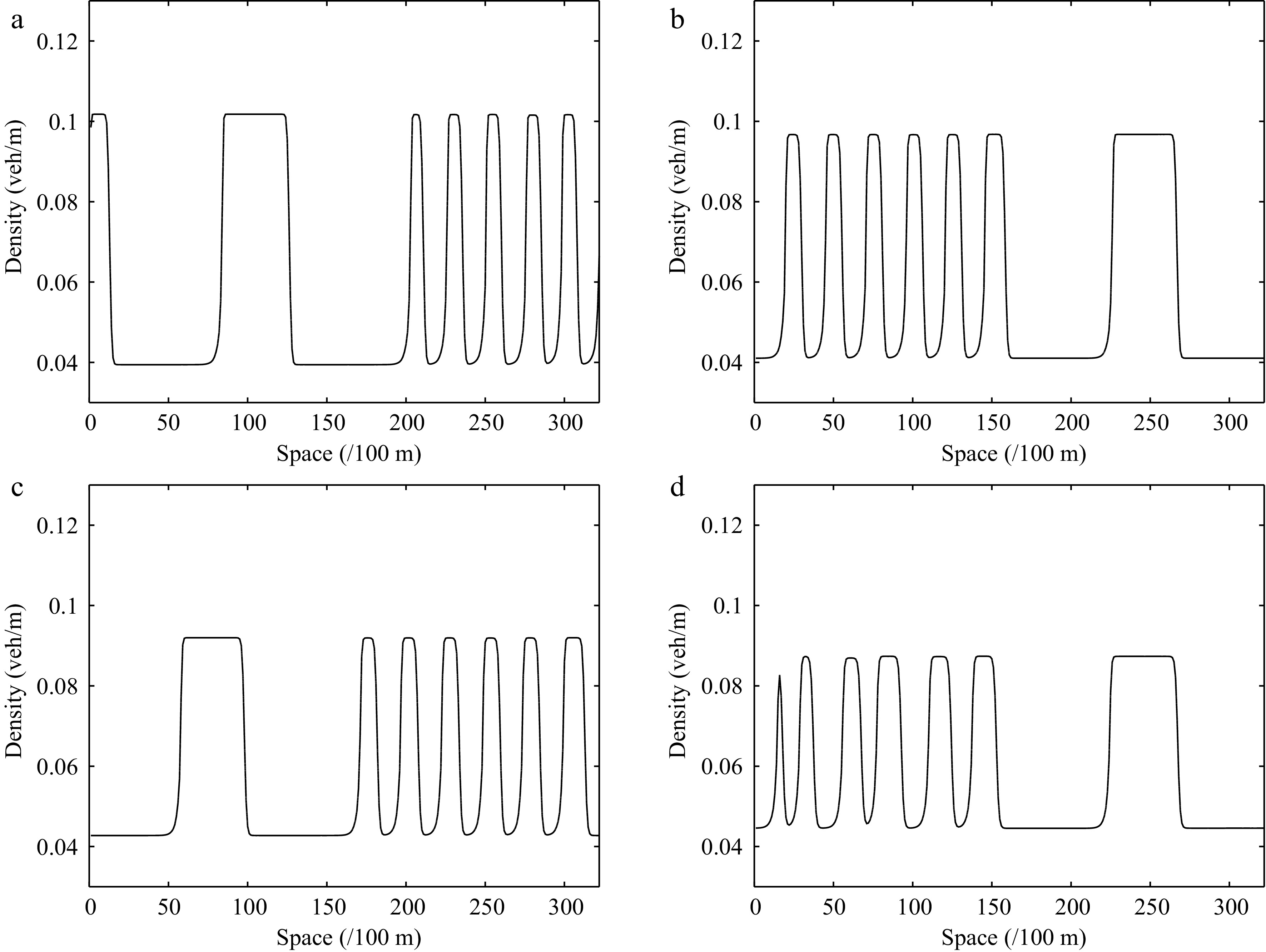
    • Figure 15. 

      Instantaneous density distribution of traffic flow corresponding to Fig. 14 at t = 3,000 s.

    • AuthorsCharacteristicsReferences
      Mohan R, Chen RHeterogeneous traffic flow[25−27]
      Lu SHigher-order[28,29]
      Liu H, Cheng RTraffic jerk effect[30,31]
      Hao L, Yu L.Delay effect[32,33]
      Liu Z, Zhai CTaillight effect[34,35]
      Jiao Y, Zhai CBackward looking effect[36,37]
      Cheng R, Zhai QMemory effect[38−40]
      Cheng R, Wang ZDriver's characteristics[41,42]
      Zhai C, Chen JSlope road / Gradient highways[43,44]
      Xue Y, Liu ZCurved road[45,46]
      Guan X, Peng GAnticipation effect[47,48]
      Ngoduy D, Bouadi MStochastic continuum models[49,50]
      Wang Z, Tang TDriver’s bounded rationality[51,52]

      Table 1. 

      Representative literature on continuum models.

    • SymbolsDefinition
      nThe subscript of vehicles
      aDriver's sensitivity
      $ {v_n} $The instantaneous velocity of vehicle n
      $ \Delta {x_n} $The instantaneous headway of vehicle n
      $ {V^{op}}( \cdot ) $Optimal velocity function
      $ {v_{\max }} $The maximum allowable driving velocity under regular road scenes
      $ {y_s} $Safety distance without collisions under regular road scenes
      $ \lambda $Sensitivity coefficient of the velocity difference
      $ H( \cdot ) $Heaviside function
      $ {s_n} $Instantaneous position information of vehicle n on the gyroidal road, and $ {s_n} = r \times {\varphi _n} $
      $ \Delta {s_n} $Instantaneous headway information of vehicle n on the gyroidal road, and $ \Delta {s_n} = r \times \Delta {\varphi _n} $
      $ r $The radius of curvature, where $ r = {\gamma \mathord{\left/ {\vphantom {\gamma {\cos \theta }}} \right. } {\cos \theta }} $
      $ \gamma $The radius of the circle
      $ \theta $Slope angle, $ \theta < 0 $ and $ \theta > 0 $ corresponding to downhill and uphill scenes respectively
      $ V( \cdot ) $Optimal speed function on the gyroidal road
      $ {\omega _{\max }} $The maximum allowable angular velocity on gyroidal roads
      $ {y_s}\left( \theta \right) $The minimum allowable safety distance on gyroidal roads, where $ {y_s}\left( \theta \right) = {y_s}\left( {1 - \alpha \sin \theta } \right) $
      $ \alpha $Is a constant. Here, we set it as $ \alpha = 1 $
      $ {v_{g,\max }} $Maximum reduced or enhanced speed on the gyroidal road, to simplify the calculation, we set $ {v_{g,\max }} = \sin \theta $
      $ m $The mass of vehicles
      $ g $Gravitational acceleration information, where we set g = 9.8 m·s−1
      $ \mu $Lateral friction coefficient
      $ k $The adjustment coefficient; here k = 0.1
      $ l $The number of vehicles ahead considered

      Table 2. 

      Primary notations used in the proposed model.

    • ParameterValueUnit
      vf30m/s
      L20km
      cm11−
      ρm0.2veh/m
      a0.3s−1
      λ0.3−
      k0.1−
      g9.8m/s2
      r60m
      l3−
      ∆t1s
      ∆x100m

      Table 3. 

      Parameter settings corresponding to Case I.

    • ParameterValueUnit
      vf30m/s
      L32.2km
      ρm0.2veh/m
      a0.34s−1
      λ0.3−
      k0.1−
      g9.8m/s2
      ∆t1s
      ∆x100m

      Table 4. 

      Parameter settings.