Figures (7)  Tables (5)

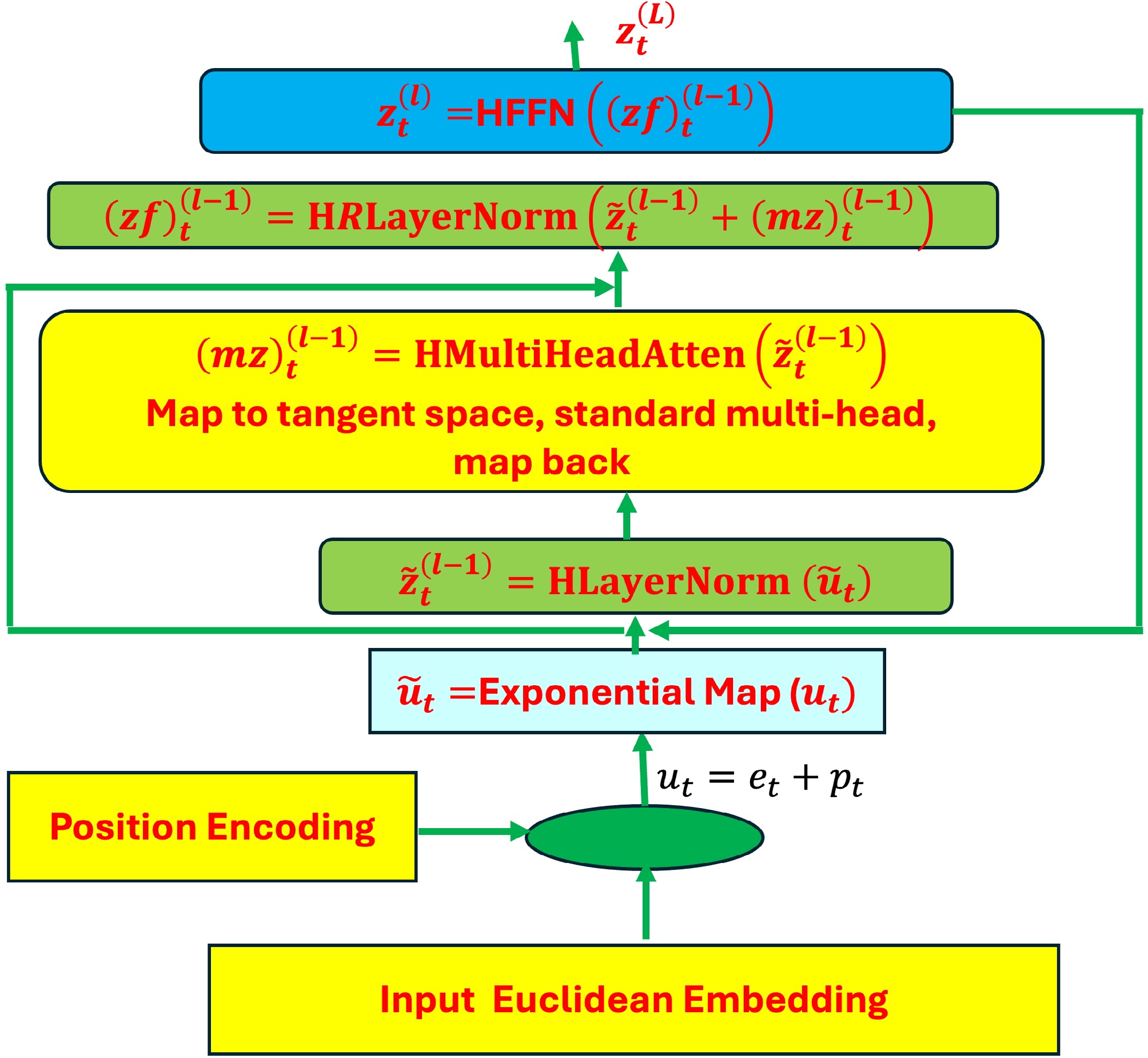
    • Figure 1. 

      Architecture of hyperbolic transformers. All steps: input Euclidean embedding, position encoding, hyperbolic layer normalization, hyperbolic multi-head attention, and hyperbolic feed-forward neural networks in the hyperbolic transformer encoder block.

    • Figure 2. 

      Transition function learning. A hyperbolic transformer is employed to learn the dynamics of the environment by modeling the transition function in RL, which describes how the environment transitions from the current state s to the next state s' and issues rewards r in response to the actions taken by the agent.

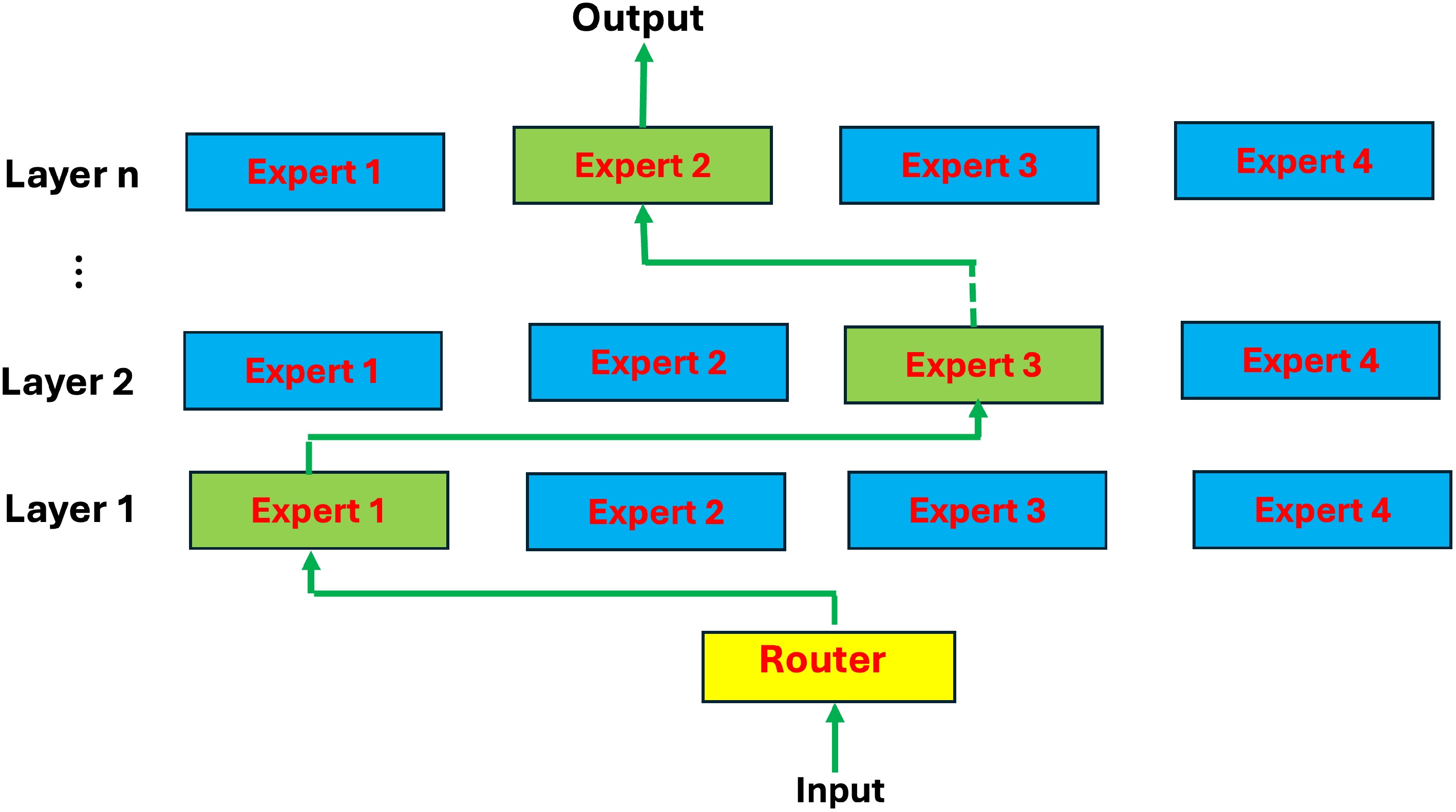
    • Figure 3. 

      Outline of MoE. The MoE has two main components, namely experts and the router: experts − each FNN layer now has a set of 'experts' which are subsets in the FNN. Router or gate network − the router determines how input tokens’ information passes experts. The MoE replaces FFN in the transformer.

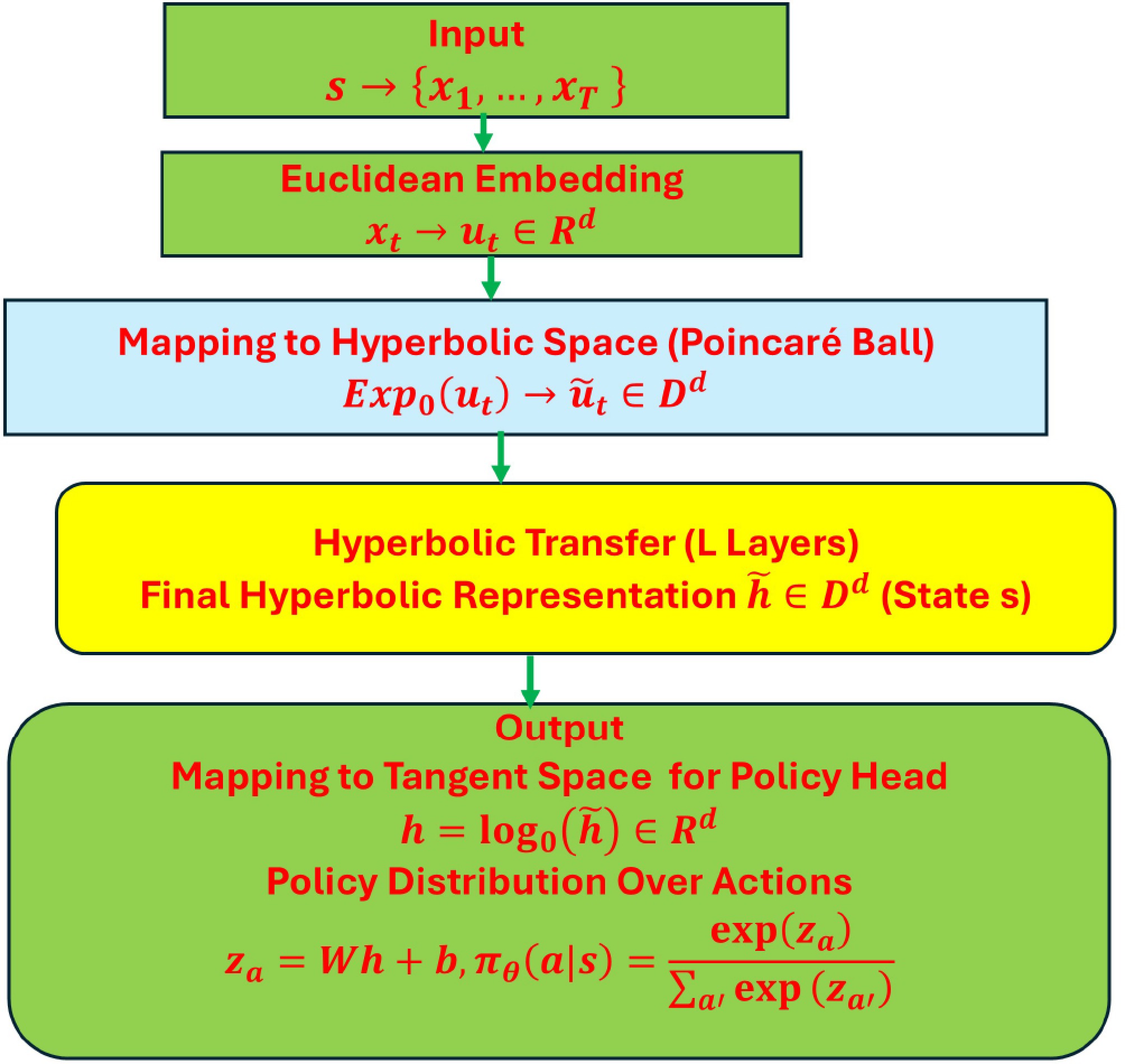
    • Figure 4. 

      Hyperbolic transformer as a policy.

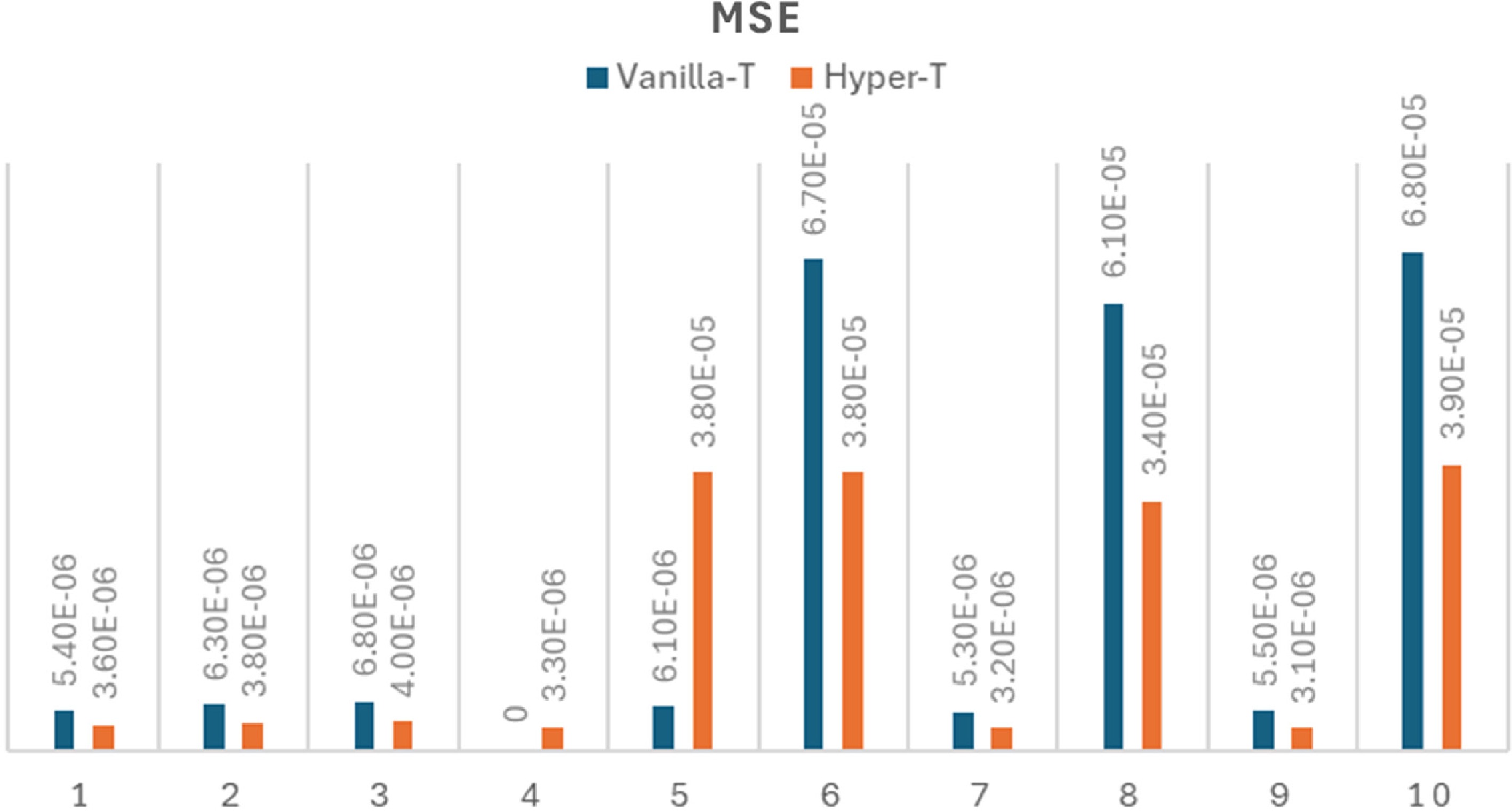
    • Figure 5. 

      MSE of vanilla-transformer and hyperbolic-transformer for solving ten FrontierMath problems (excluding A.11 sample problem 11 - prime field continuous extensions).

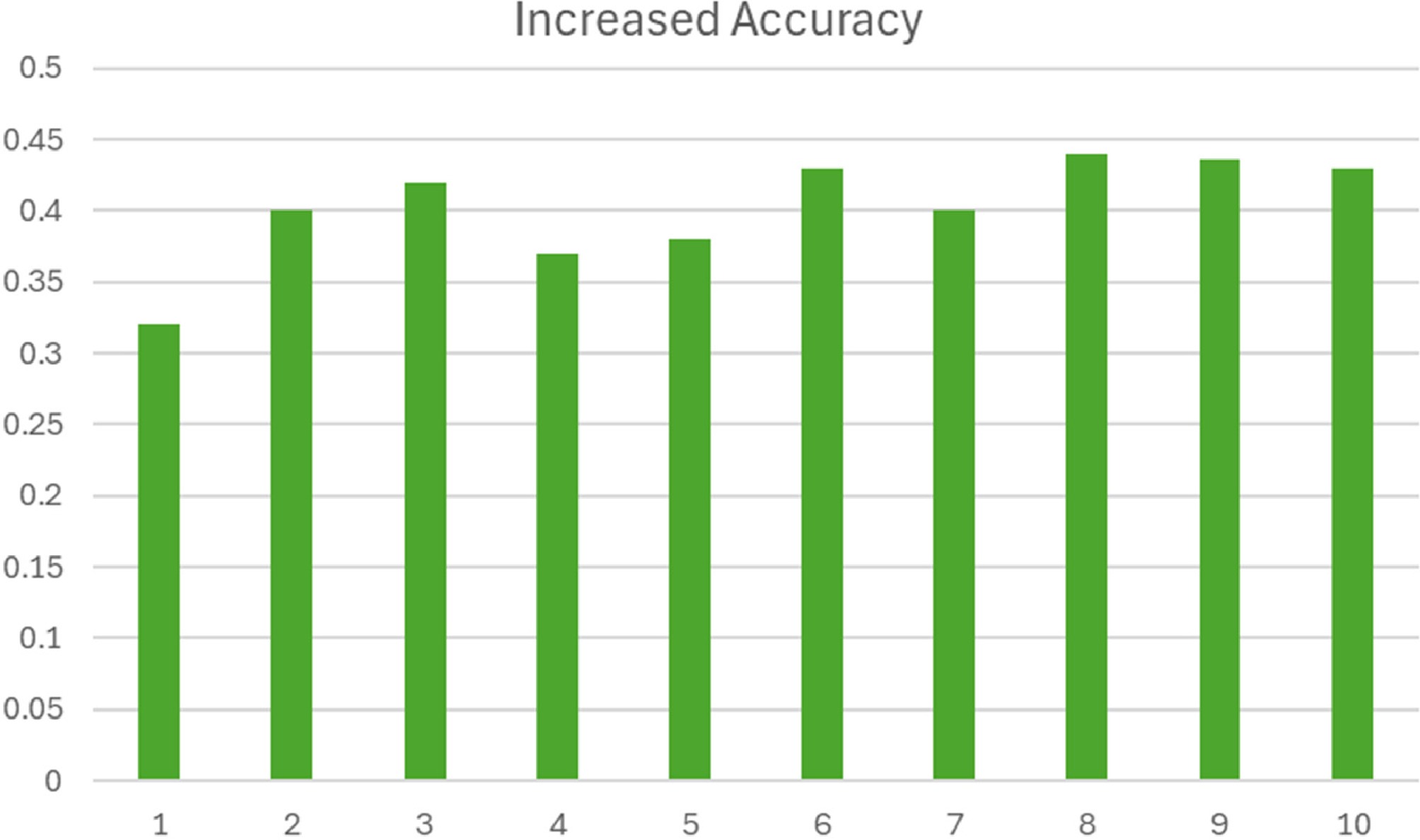
    • Figure 6. 

      The increased accuracy of the Hyper-T vs Vanilla-T.

    • Figure 7. 

      Wall-ClockHyper-T for 11 FrontierMath problems.

    • Input: θ0: hyperbolic transformer, Manifold: the Poincaré ball, group G, clip ε
      Initialize policy πθ and hyperbolic transformer
      for k = 0, 1, 2, ...
      for env episode e = 1, ..., B
      1. Sample collection from the policy
      A batch of N states $ {\{{s}^{\left(j\right)}\}}_{j=1}^{N} $ sampled from the environment using the policy $ {\pi }_{{\theta }_{k}} $.
      For each state s(j), generate G responses: a set (or group) of G actions is sampled: $ \left\{{a}_{1}^{\left\{j\right\}}, \dots ,{a}_{G}^{\left\{j\right\}}\right\} $ from human preference feedback in the population, get the group information and divide samples into diverse and robust group, returns a reward $ r\left({s}^{\left(j\right)},{a}^{\left(j\right)}\right) $.
      With batch
      2. Compute group-based (relative) advantage
      Define the group statistics for each state s(j) and its corresponding group of actions, then, defining the group-relative advantage for each action $ {a}_{i}^{\left(j\right)} $; For each $ \left({s}^{\left(j\right)},{a}_{i}^{\left(j\right)}\right) $, evaluate the new policy’s probability using the hyperbolic transformer $ {\pi }_{{\theta }_{k}}\left({a}_{i}^{\left(j\right)}|{s}^{\left(j\right)}\right) $ and compute the probability ratios relative to the old policy and reference, and K-L distance $ {D}_{KL}\left({\pi }_{{\theta }_{k}}\left|\right|{\pi }_{ref}\right) $.
      3. Form the GRPO surrogate objective $ L\left({s}^{\left(j\right)},{\theta }_{k}\right) $ and the total surrogate objective over the batch $ L\left({\theta }_{k}\right)=\dfrac{1}{N}{\sum }_{j=1}^{N}L\left({s}^{\left(j\right)},{\theta }_{k}\right). $
      End batch
      4. Gradient ascent through hyperbolic transformations and hyperbolic-aware optimization for updating parameters.
      End k

      Table 1. 

      hyperbolic GRPO.

    • Backbone Updates to MAE < 10−6 Final MAE × 10−6 Wall-clock
      Vanilla-T 10,200 ± 800 6.2 1
      Hyperbolic-T 6,600 ± 610 3.1 0.84 ×

      Table 1. 

      Comparison between vanilla transformer and hyperbolic transformer on the scalar root-finding benchmark.

    • Backbone Updates to hit 11 Miss.pred.rate (%) Wall-clock
      Vanilla-T 10,400 ± 800 0.46 1.00
      Hyper-T 6,900 ± 600 0.31 0.83

      Table 2. 

      Comparison between vanilla transformers and hyperbolic transformers on the Prime field continuous extension problem.

    • Backbone Updates to MAE < 10−6 Final MAE × 10−6 Wall-clock
      Vanilla-T 12,800 ± 900 6.4 1.00
      Hyper-T 8,200 ± 670 3.6 0.83

      Table 3. 

      Comparison between vanilla transformer and hyperbolic transformers on the Van-der-Pol optimal-control problem.

    • Backbone Updates to MAE < 10−6 Final MAE ×10−6 Wall-clock
      Vanilla-T 10,500 ± 800 6.0 1.00
      Hyper-T 6,800 ± 620 3.3 0.84

      Table 4. 

      Comparison between vanilla transformer and hyperbolic transformers on the unicycle–vehicle energy-minimization problem.