Figures (8)  Tables (7)

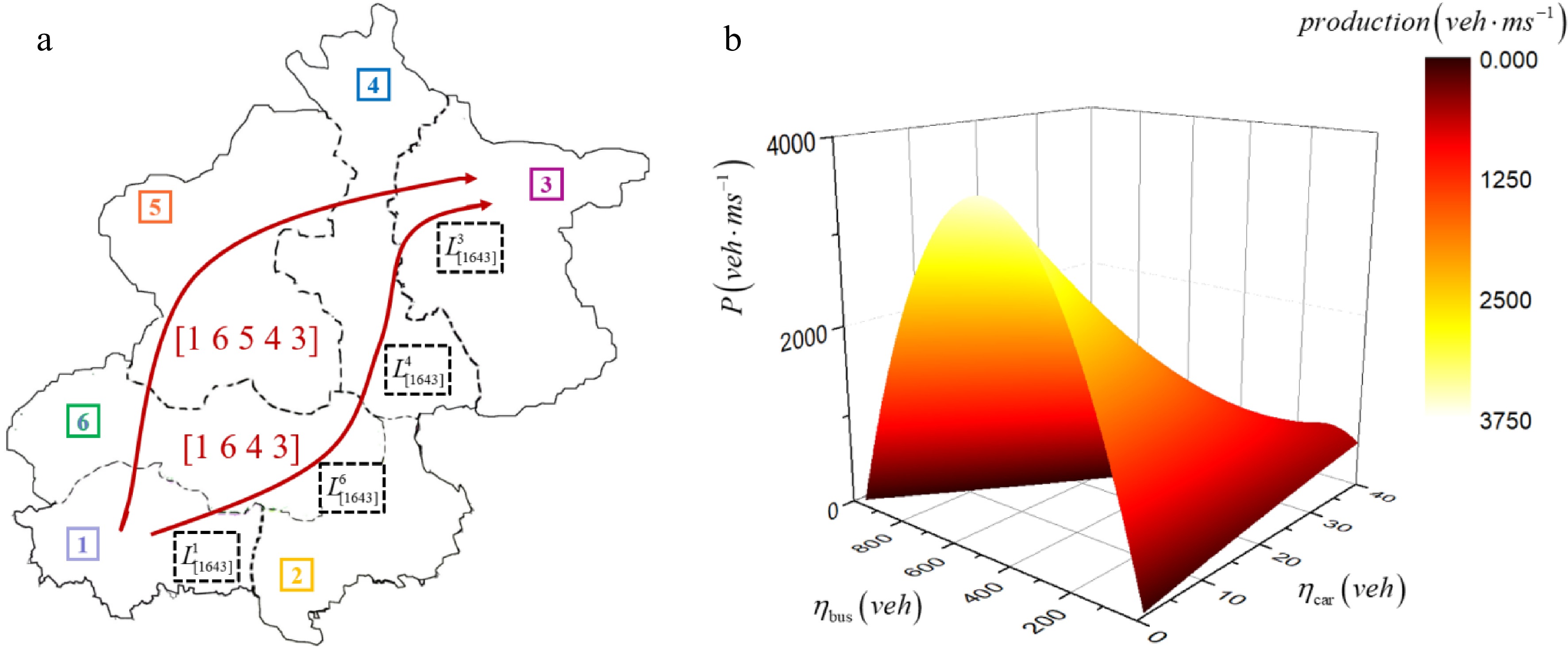
    • Figure 1. 

      A multi-reservoir network. (a) Network partitioning and characteristics. (b) 3D-MFD surface which the formula refers to Paipuri & Leclercq[27].

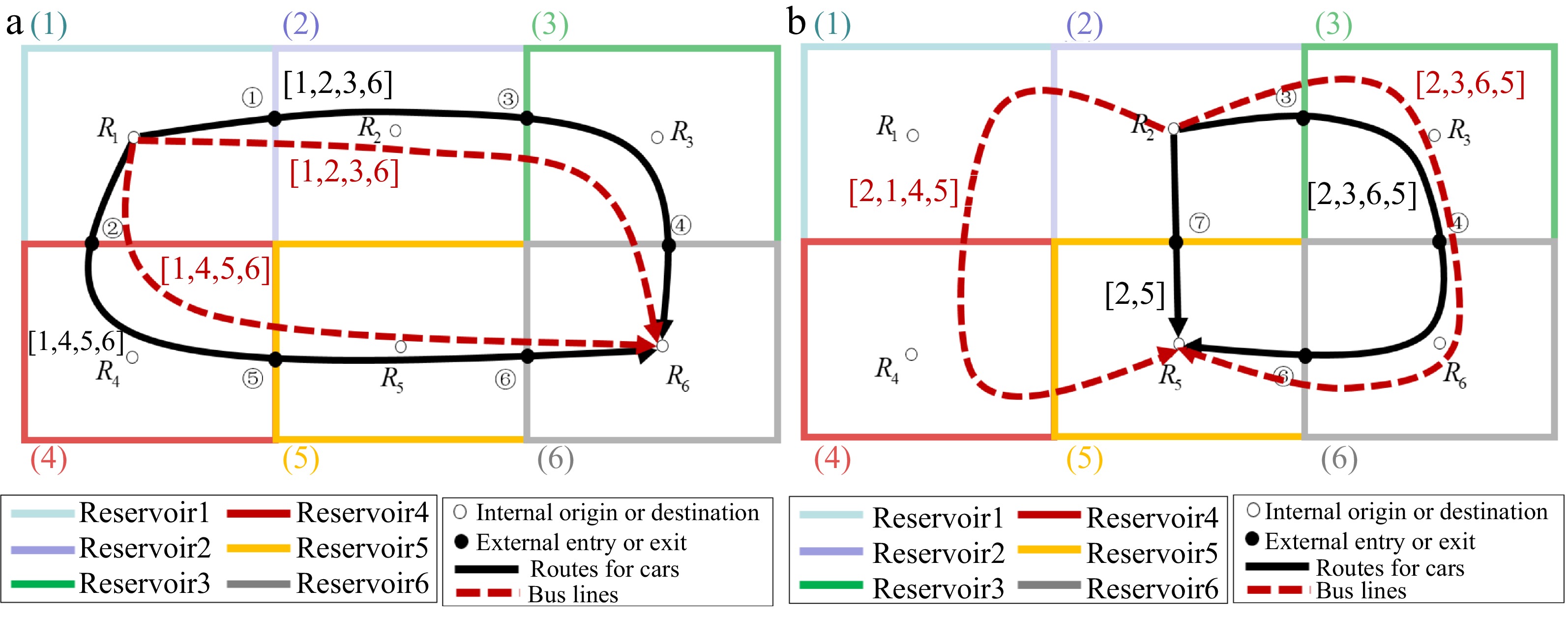
    • Figure 2. 

      Reservoir system configuration. (a) The regional OD pair (1−6). (b) The regional OD pair (2−5).

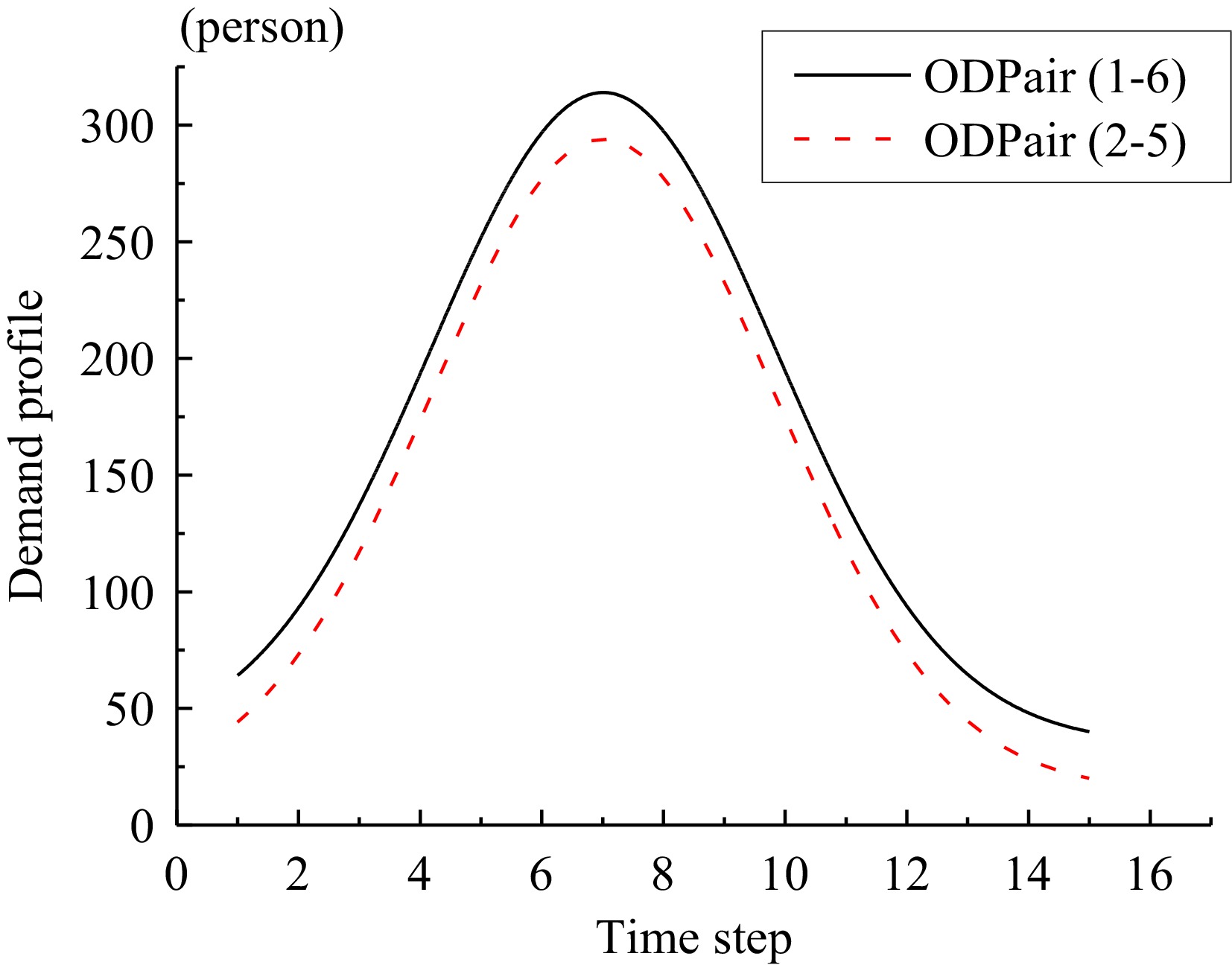
    • Figure 3. 

      OD demand profile.

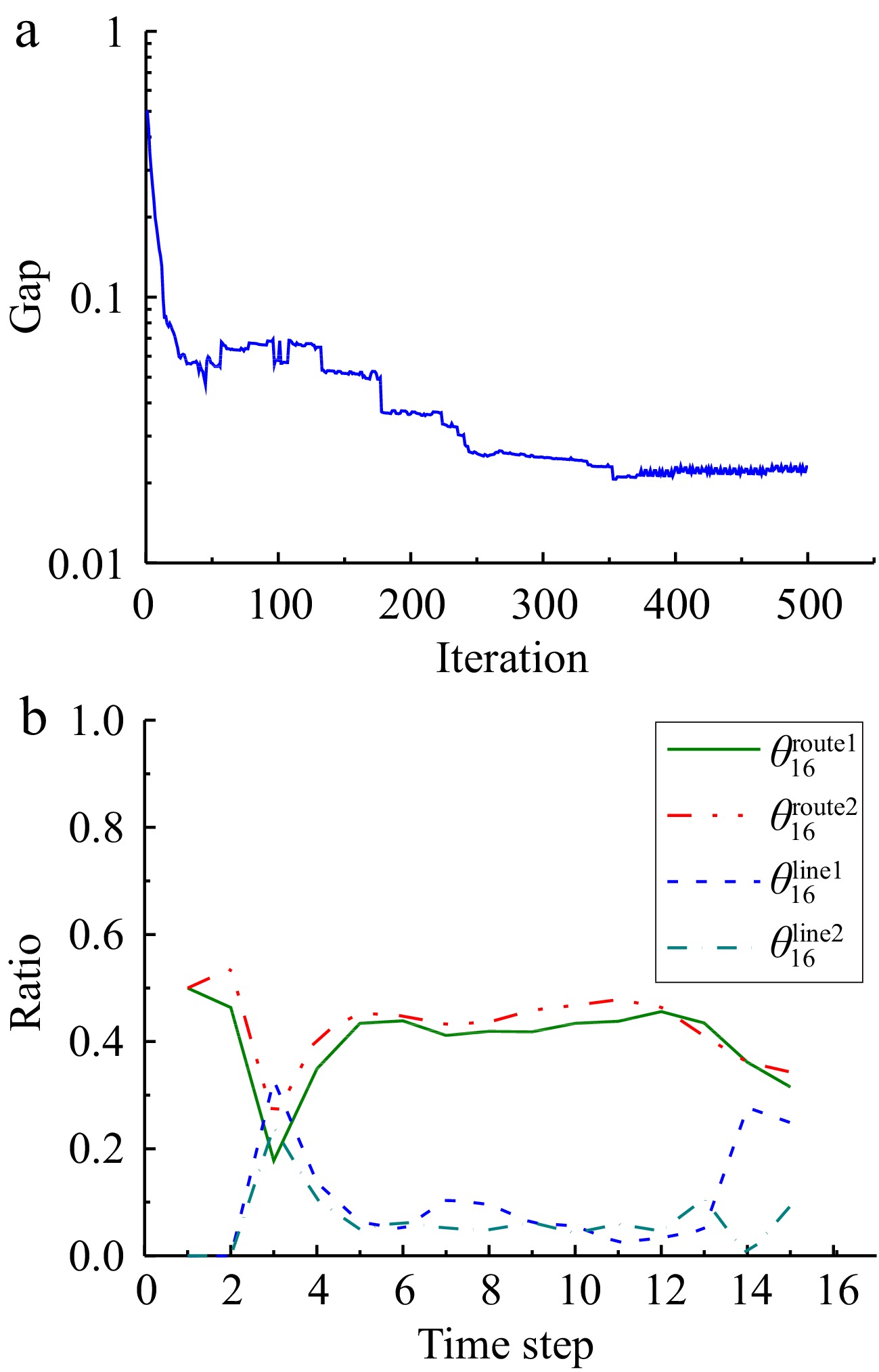
    • Figure 4. 

      Results using double projection algorithm. (a) Convergence of double projection algorithm. (b) Route choice parameters for an OD pair.

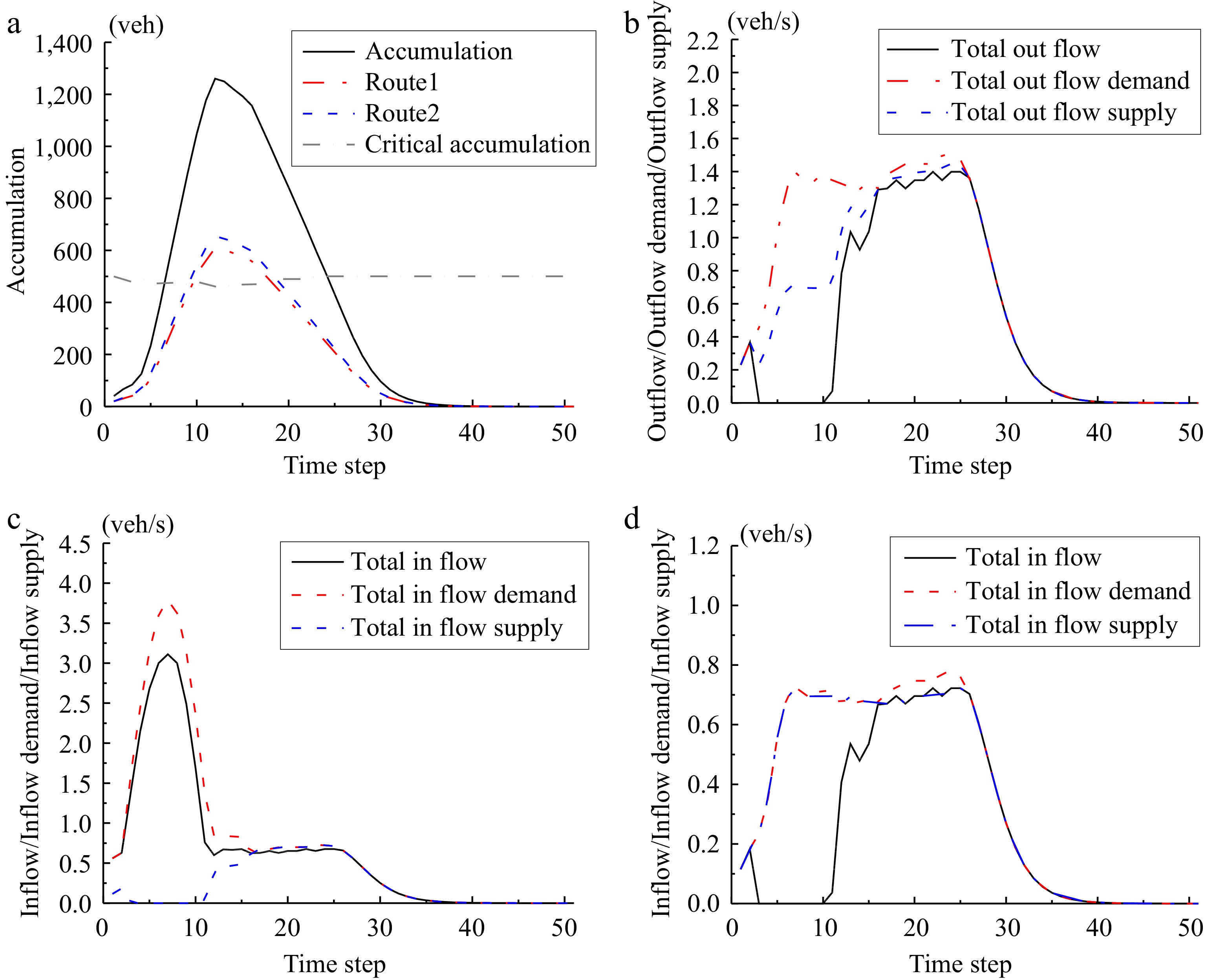
    • Figure 5. 

      Traffic dynamics. (a) Evolution of car accumulation in Reservoir 1. (b) Evolution of outflow in Reservoir 1. (c) Evolution of inflow in Reservoir 2. (d) Evolution of inflow in Reservoir 4.

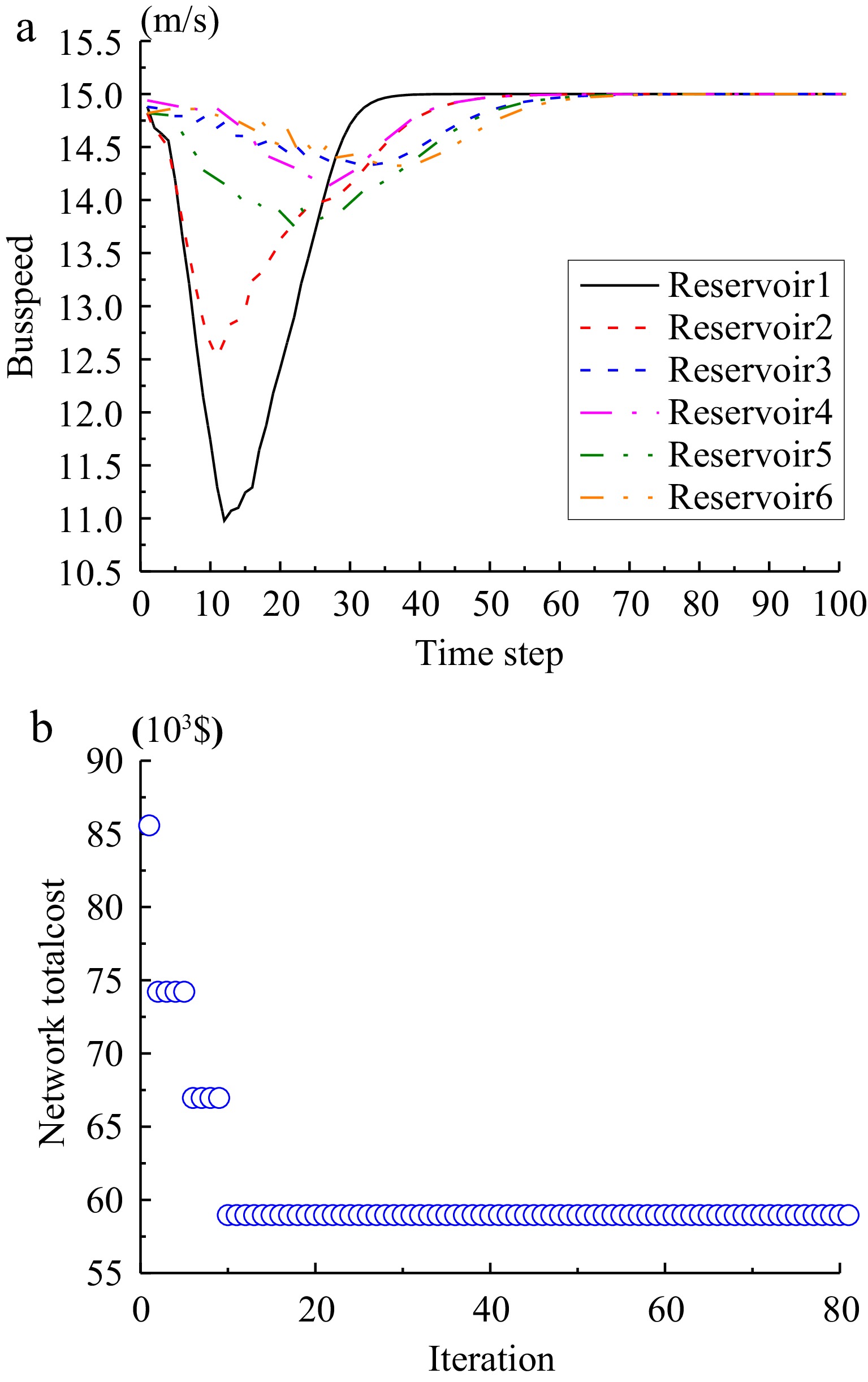
    • Figure 6. 

      Results on the (a) bus speed evolution and (b) convergence of the surrogate model based algorithm.

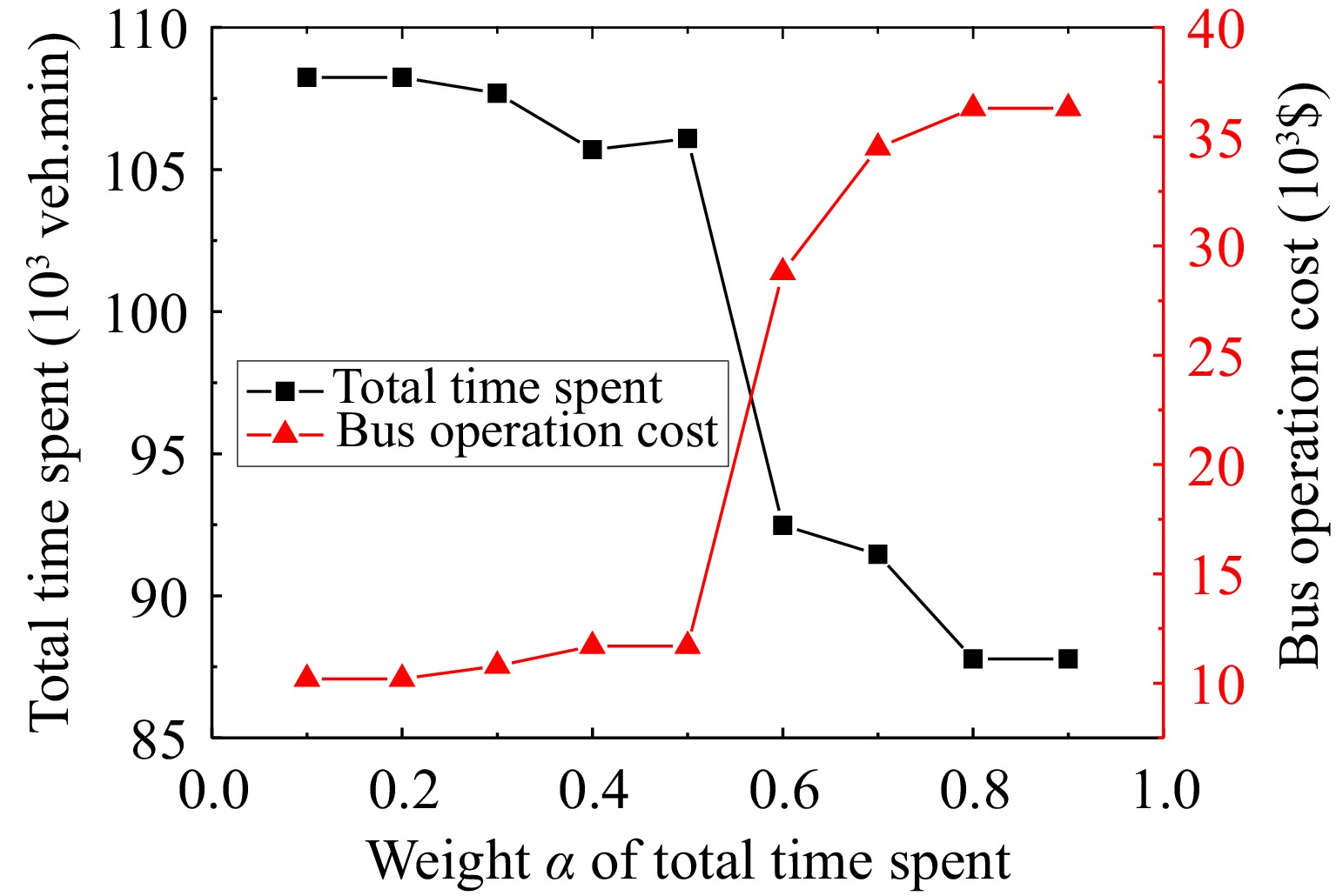
    • Figure 7. 

      Changes in the total time spent and bus operation cost for different weight values (α).

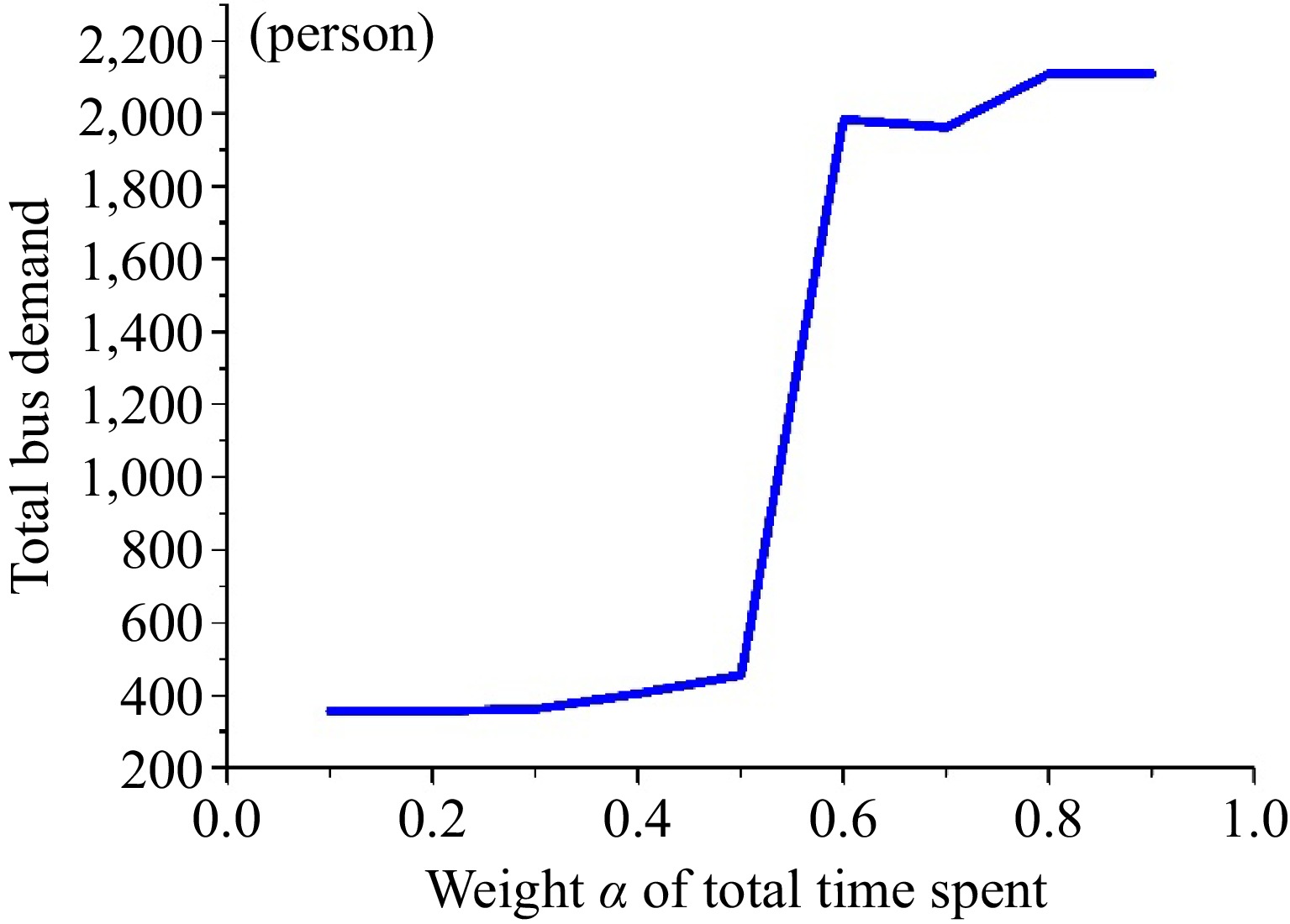
    • Figure 8. 

      The influence of the total time spent on the demand for bus travel.

    • Input: Reservoir initial bus accumulation $\eta _{{\text{p,r}}}^{{\text{bus}}}\left( {{t_0}} \right)$ of each path, car accumulation $\eta _{{\text{p,r}}}^{{\text{car}}}\left( {{t_0}} \right)$ of each path, initial trip distance $L_{{\text{p,r,t}}}^{{\text{bus}}}\left( {{t_{\text{0}}}} \right){\text{ = 0}}$, the subscript $t$ represents the bus departing at time $t$, traffic demand profile $\lambda _{\text{p}}^{{\text{w,bus}}}\left( t \right)$, simulation duration $T$ and time step $\delta t$.
      1: for $t = {t_0}$ to ${t_0} + T$ by $\delta t$ do
      2: According to the bus and car accumulation which is calculated by Eq. (1), combined with reservoir 3D-MFD, the bus speed $v_{\text{r}}^{{\text{bus}}}\left( t \right)$ is determined by Eq. (11)
      3: for $r = 1$ to $N$ do
      4: Inflow: if $r = o$ then $\eta _{{\text{p,r,in}}}^{{\text{bus}}}\left( t \right) = \lambda _{\text{p}}^{{\text{w,bus}}}\left( t \right) \cdot \delta t$ else $\eta _{{\text{p,r,in}}}^{{\text{bus}}}\left( t \right) = \eta _{{\text{p,}}{{\text{p}}^{\text{ - }}}\left( {\text{r}} \right){\text{,out}}}^{{\text{bus}}}\left( t \right)$
      5: Outflow: track the trip distance $L_{{\text{p,r,t}}}^{{\text{bus}}}\left( {t{\text{ + }}\delta t} \right) = L_{{\text{p,r,t}}}^{{\text{bus}}}\left( t \right) + v_{\text{r}}^{{\text{bus}}}\left( t \right) \cdot \delta t$
      6: if $L_{{\text{p,r,t}}}^{{\text{bus}}}\left( {t{\text{ + }}\delta t} \right) > L_{{\text{p,r}}}^{{\text{bus}}}$
      7: if $r = d$ then $ {\tau _{{\text{p,bus,travel}}}}\left( t \right) = {\tau _{{\text{p,bus,travel}}}}\left( t \right) + {t_{\text{s}}} $, $\eta _{{\text{p,r,out}}}^{{\text{bus}}}\left( t \right) = \eta _{{\text{p,r,in}}}^{{\text{bus}}}\left( {t{\text{ - }}{\tau _{{\text{p,bus,travel}}}}\left( t \right)} \right)$
      where ${t_{\text{s}}}$ is the traveling time in reservoir $r$.
      8: else ${\tau _{{\text{p,bus,travel}}}}\left( t \right) = {\tau _{{\text{p,bus,travel}}}}\left( t \right) + \delta t$, $\eta _{{\text{p,r,out}}}^{{\text{bus}}}\left( t \right) = \eta _{{\text{p,r,in}}}^{{\text{bus}}}\left( {t{\text{ - }}{\tau _{{\text{p,bus,travel}}}}\left( t \right)} \right)$
      9: else ${\tau _{{\text{p,bus,travel}}}}\left( t \right) = {\tau _{{\text{p,bus,travel}}}}\left( t \right) + \delta t$, $\eta _{{\text{p,r,out}}}^{{\text{bus}}}\left( t \right) = 0$
      10: Bus accumulation update: $\eta _{{\text{p,r}}}^{{\text{bus}}}\left( {t + \delta t} \right) = \eta _{{\text{p,r}}}^{{\text{bus}}}\left( t \right) + \eta _{{\text{p,r,in}}}^{{\text{bus}}}\left( t \right) - \eta _{{\text{p,r,out}}}^{{\text{bus}}}\left( t \right)$
      11: end for
      12: end for
      Output: reservoir bus accumulation $\eta _{{\text{p,r}}}^{{\text{bus}}}\left( t \right)$, the experienced travel time ${\tau _{{\text{p,bus,travel}}}}\left( t \right)$

      Table 1. 

      Trip-based solver algorithm.

    • Input: projection step $\bar \rho $, accuracy $\varepsilon > 0$, select parameters $\beta $, $ \xi \in \left(\text{0}，\text{1}\right) $, path set ${P^{\text{w}}}$
      1:Initial path demand ${{\mathbf{f}}^0}\left( k \right) = {\lambda ^{\text{w}}}\left( k \right)/\varsigma $, $\varsigma $ is the sum of path between OD pair $w$, the dynamic travel
      time ${\mathbf{\tau }}$ of all path is obtained in section "Lower-level problem". Set ${\rho ^0} = \bar \rho $, iteration $\gamma = 0$.
      2:while $G({{\mathbf{f}}^{\text{γ }}}) > \varepsilon $
      3: Compute ${{\mathbf{\bar f}}^{\text{γ }}}(k) = {\text{pro}}{{\text{j}}_\Omega }({{\mathbf{f}}^{\text{γ }}}(k) - {\rho ^{\text{γ }}}{\mathbf{\tau }}({{\mathbf{f}}^{\text{γ }}}(k)))$
      4: while ${\rho ^{\text{γ }}} > \beta \frac{{\left\| {{{\mathbf{f}}^{\text{γ }}}(k) - {{{\mathbf{\bar f}}}^{\text{γ }}}(k)} \right\|}}{{\left\| {{\mathbf{\tau }}({{\mathbf{f}}^{\text{γ }}}(k)) - {\mathbf{\tau }}({{{\mathbf{\bar f}}}^{\text{γ }}}(k))} \right\|}}$ do
      5: ${\rho ^{\text{γ }}} = \min \left\{ {\xi {\rho ^{\text{γ }}},\beta \frac{{\left\| {{{\mathbf{f}}^{\text{γ }}}(k) - {{{\mathbf{\bar f}}}^{\text{γ }}}(k)} \right\|}}{{\left\| {{\mathbf{\tau }}({{\mathbf{f}}^{\text{γ }}}(k)) - {\mathbf{\tau }}({{{\mathbf{\bar f}}}^{\text{γ }}}(k))} \right\|}}} \right\}$
      6: Compute ${{\mathbf{\bar f}}^{\text{γ }}}(k) = {\text{pro}}{{\text{j}}_\Omega }({{\mathbf{f}}^{\text{γ }}}(k) - {\rho ^{\text{γ }}}{\mathbf{\tau }}({{\mathbf{f}}^{\text{γ }}}(k)))$
      7: end while
      8: Compute ${{\mathbf{f}}^{{\text{γ + 1}}}}(k) = {\text{pro}}{{\text{j}}_\Omega }({{\mathbf{f}}^{\text{γ }}}(k) - {\rho ^{\text{γ }}}{\mathbf{\tau }}({{\mathbf{\bar f}}^{\text{γ }}}(k)))$
      9: Update travel time vector ${\mathbf{\tau }}({{\mathbf{f}}^{\gamma + 1}}(k))$ by the dynamic network loading models in previous section. Set $\gamma = \gamma + 1$
      10:end while
      Output: flow vector ${{\mathbf{f}}^{\text{γ }}}(k)$

      Table 2. 

      Double projection algorithm.

    • Input: the maximum iterations ${\gamma _{\max }}$, the maximum consecutive successes $ C_{{\text{success}}}^{{\text{max}}} $, the maximum consecutive failures $ C_{{\text{fail}}}^{{\text{max}}} $, the initial disturbance probability $ p_{{\text{slct}}}^{{\text{init}}} $.
      1:Initialization
      1.1 initial evaluation points set. ${I_0} = \left\{ {{{\mathbf{y}}_1},{{\mathbf{y}}_2}, \ldots ,{{\mathbf{y}}_{{{\text{n}}_{\text{0}}}}}} \right\}$, the number of evaluation points is ${n_0}$, the real objective function value vector ${\mathbf{Z}} = \left[ {Z\left( {{{\mathbf{y}}_{\text{i}}}} \right),{{\mathbf{y}}_{\text{i}}} \in {I_0}} \right]$ corresponding to each evaluation point ${{\mathbf{y}}_{\text{i}}} = \left\{ {{{\left\{ {{f_1},{f_2}, \ldots ,{f_{{{\text{n}}_{\text{0}}}}}} \right\}}^{\text{i}}}} \right\}$ (evaluation point is the bus frequency planning of each line) is calculated, and the best feasible solution with the minimum objective value $Z\left( {{{\mathbf{y}}_{\text{i}}}} \right)$ as the current optimal solution ${{\mathbf{y}}_{{\text{best}}}}$, set the iterate number $\gamma = 0$.
      1.2 initialization parameters. Initialize the counters of consecutive successes ${C_{{\text{sucess}}}} = 0$, the counters of consecutive failures ${C_{{\text{fail}}}} = 0$, the maximum number of consecutive updating success and failure of the optimal solution are $C_{{\text{success}}}^{\max }$ and $C_{{\text{fail}}}^{{\text{max}}}$, set the disturbance probability $p_{{\text{slct}}}^{\text{0}} = p_{{\text{slct}}}^{{\text{init}}}$.
      2:Repeat
      3:Update surrogate model.
      Use the evaluation point set ${I_{\text{n}}}$ and Eq. (14) to calculate the corresponding objective function value ${\prod _{\text{n}}} = \left\{ {\left( {{{\mathbf{y}}_{\text{i}}},Z\left( {{{\mathbf{y}}_{\text{i}}}} \right)} \right),{{\mathbf{y}}_{\text{i}}} \in {I_{\text{n}}}} \right\}$, and update the surrogate model ${S_{\text{n}}}\left( {\mathbf{y}} \right)$ refer to Liu[50].
      4:Candidate points set generation.
      Based on the perturbation probability $ {p_{{\text{slc}}t}} $, the candidate points set ${E_{\text{n}}}$ is generated by perturbing the value of any variable in the current optimal solution ${{\mathbf{y}}_{{\text{best}}}}$. When generating candidate points, ensure that each candidate point meets the investment constraint Eq. (15).
      5:Select the evaluation point.
      Each candidate point is scored. Set ${{\mathbf{y}}_{{\text{n+1}}}}$ as the best candidate and calculate $Z({{\mathbf{y}}_{{\text{n+1}}}})$.
      7:Update the optimal solution.
      If $Z({{\mathbf{y}}_{{\text{n+1}}}}) < Z({{\mathbf{y}}_{{\text{best}}}})$, then update the optimal solution ${{\mathbf{y}}_{{\text{best}}}} = {{\mathbf{y}}_{{\text{n+1}}}}$ and $Z({{\mathbf{y}}_{{\text{best}}}}){\text{ = }}Z({{\mathbf{y}}_{{\text{n+1}}}})$, continuous success iteration ${C_{{\text{success}}}} = {C_{{\text{success}}}} + 1$ and continuous failure iteration ${C_{{\text{fail}}}} = 0$; otherwise, let ${C_{{\text{fail}}}} = {C_{{\text{fail}}}} + 1$ and ${C_{{\text{success}}}} = 0$.
      8:Adjust disturbance probability.
      If $ {C_{{\text{success}}}} > C_{{\text{success}}}^{{\text{max}}} $, then $ p_{{\text{slct}}}^{{\text{n+1}}} = \min \{ 2p_{{\text{slct}}}^{\text{n}},p_{{\text{slct}}}^{{\text{max}}}\} $, $ {C_{{\text{success}}}} = 0 $.
      If $ {C_{{\text{fail}}}} > C_{{\text{fail}}}^{{\text{max}}} $, set $ p_{{\text{slct}}}^{{\text{n+1}}} = \max \{ p_{{\text{slct}}}^{\text{n}}/2,p_{{\text{slct}}}^{{\text{min}}}\} $ and $ {C_{{\text{fail}}}} = 0 $. Set $\gamma = \gamma + 1$.
      9:Update the evaluation points set.
      ${I_{{\text{n+1}}}} = {I_{\text{n}}} \cup \{ {{\mathbf{y}}_{{\text{n+1}}}}\} $
      10:Until $\gamma \geqslant {\gamma _{\max }}$
      Output: ${{\mathbf{y}}_{{\text{best}}}}$

      Table 3. 

      Surrogate model-based algorithm.

    • Characteristics[units]${R_1}$${R_2}$${R_3}$${R_4}$${R_5}$${R_6}$
      Trip length $L_{\text{1}}^{{\text{car}}}$[m]250050005000−−2500
      Trip length $L_{\text{2}}^{{\text{car}}}$[m]2500−−500050002500
      Trip length $L_3^{{\text{car}}}$[m]−2500−−2500−
      Trip length $L_{\text{4}}^{{\text{car}}}$[m]−25005000−25005000
      Bus line $L_{\text{1}}^{{\text{bus}}}$[m]250050005000−−2500
      Bus line $L_{\text{2}}^{{\text{bus}}}$[m]2500−−500050003500
      Bus line $L_{\text{3}}^{{\text{bus}}}$[m]50002500−50002500−
      Bus line $L_{\text{4}}^{{\text{bus}}}$[m]−25005000−25005000

      Table 1. 

      Reservoir characteristics, where $L_{\text{1}}^{{\text{car}}}$, $L_{\text{2}}^{{\text{car}}}$, $L_3^{{\text{car}}}$, $L_{\text{4}}^{{\text{car}}}$ refer to the trip length of route 1, 2, 3, 4 and $L_{\text{1}}^{{\text{bus}}}$, $L_{\text{2}}^{{\text{bus}}}$, $L_{\text{3}}^{{\text{bus}}}$, $L_{\text{4}}^{{\text{bus}}}$ refer to the trip length of bus line 1, 2, 3, 4.

    • Simulation3D-MFD2D-MFD
      The optimal frequency (min){3.0, 4.0, 4.0, 3.0}{4.0, 0.2, 2.0, 1.0}
      Total time spent (veh·min)106088.7593111.93
      Operation cost (${\$}$)1170044400
      The objective value (${\$}$)58894.3868755.96

      Table 2. 

      Total travel time of passengers and operation cost using 3D-MFD and 2D-MFD respectively.

    • SimulationEquilibriumNon-equilibrium
      Total time spent (veh·min)106088.75177269.47
      Operation cost (min)1170035400
      The objective value $\left( {\$} \right)$58894.38106334.73

      Table 3. 

      The optimal solution under equilibrium and non-equilibrium type.

    • SimulationThe optimal
      frequency (min)      		The objective value ($ {\$} $)$\Delta {Z_{\text{i} } }$ (%)
      Scenario 1
      (2D-MFD non-equilibrium)      		{1.0, 0.5, 0.5, 0.5}68,544.69816.39
      Scenario 2
      (2D-MFD equilibrium)      		{4.0, 0.2, 2.0, 1.0}68,755.96416.74
      Scenario 3
      (3D-MFD non-equilibrium)      		{1.0, 0.5, 1.0, 1.0}65,623.04311.42
      Scenario 4
      (3D-MFD equilibrium)      		{3.0, 4.0, 4.0, 3.0}58,894.376−

      Table 4. 

      Comparison of the results of the optimal solution in 4 scenarios.