-
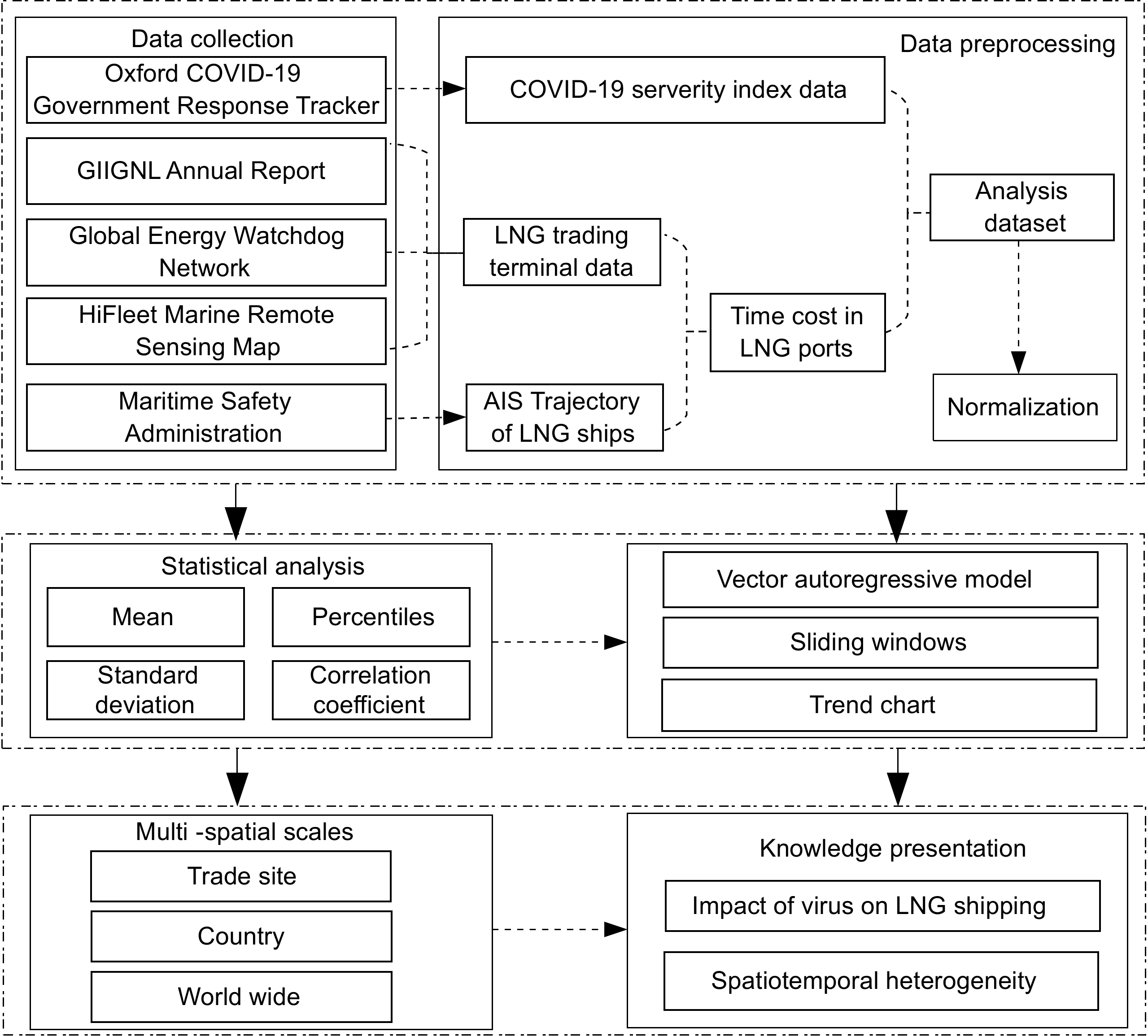
Figure 1.
Flowchart of quantitative analysis of the efficiency dynamics of global liquefied natural gas shipping under COVID-19.
-
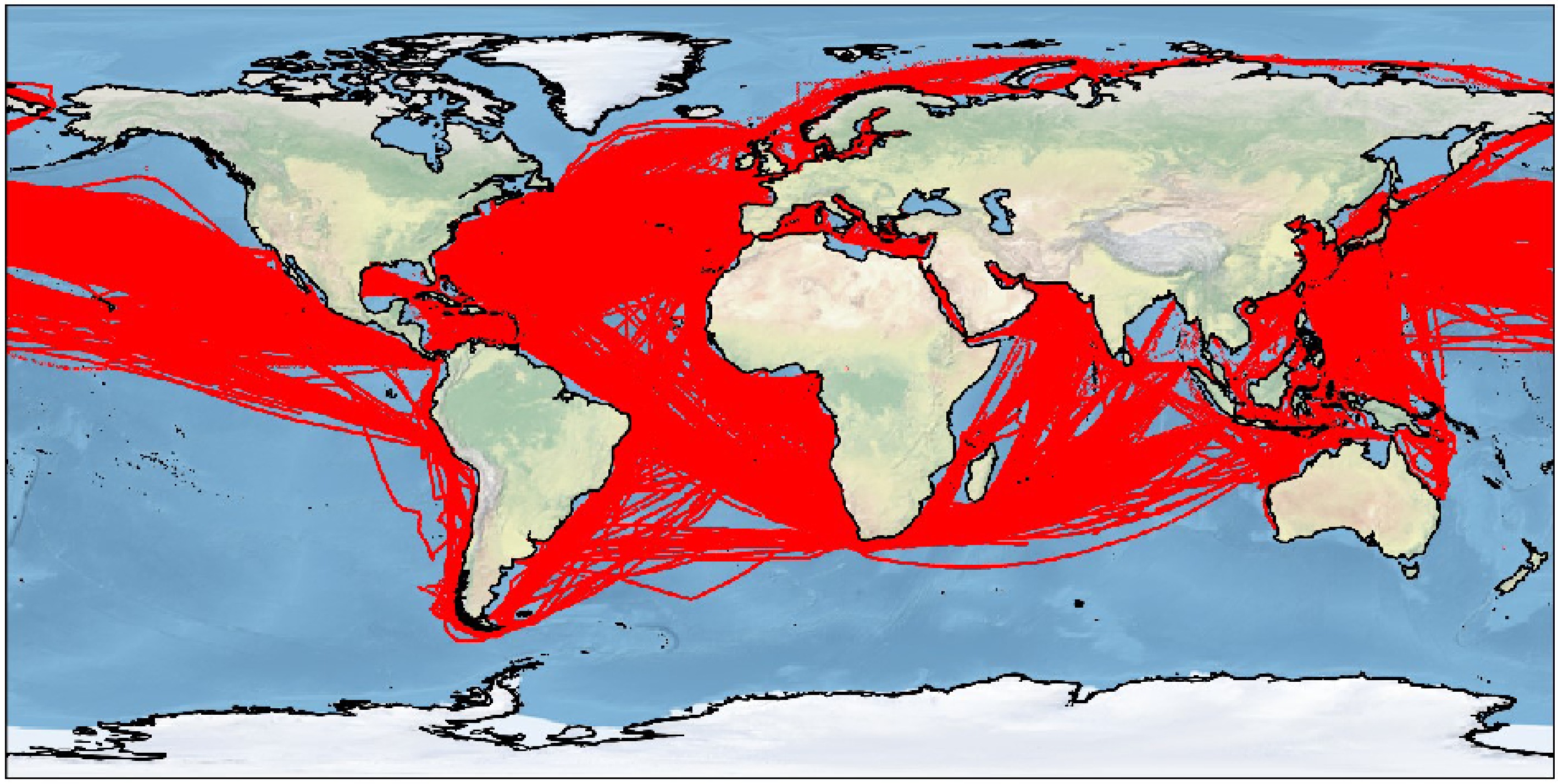
Figure 2.
AIS track chart of LNG carrier in 2021 (the global map is from ArcMap World map).
-
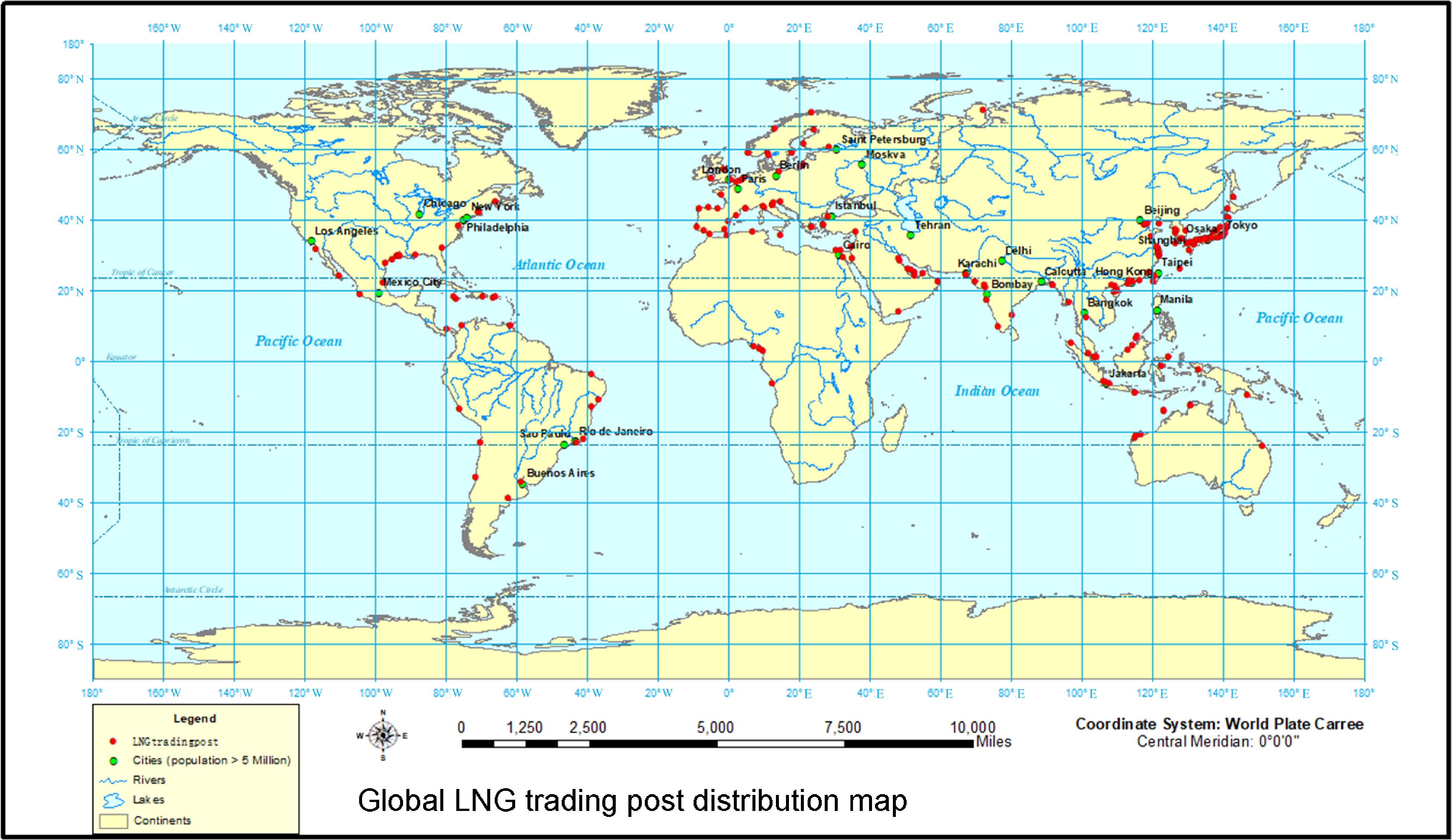
Figure 3.
Directed network of LNG shipping (the global map is from ArcMap World map).
-
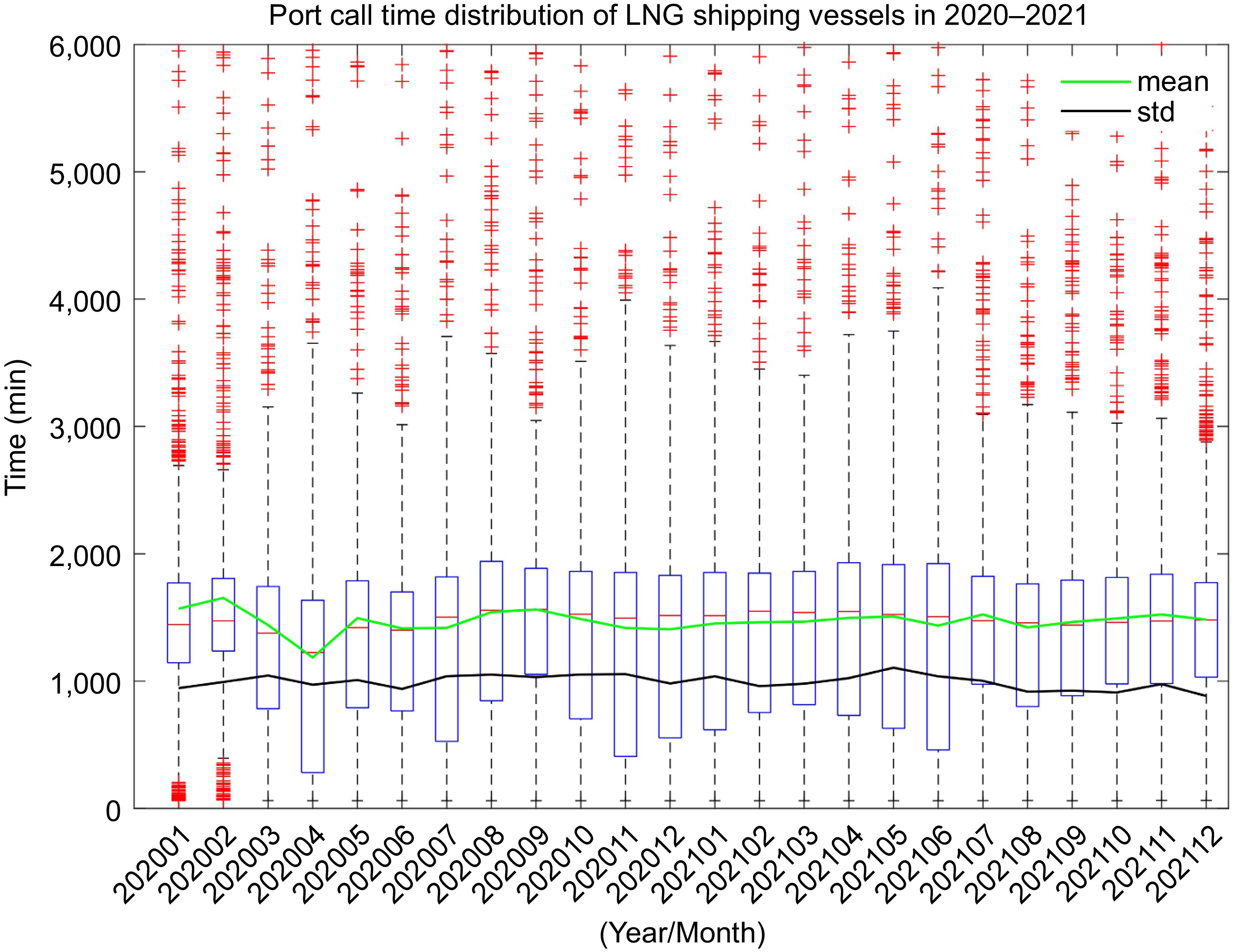
Figure 4.
Statistical analysis of LNG shipping under the pandemic in 2020 and 2021.
-
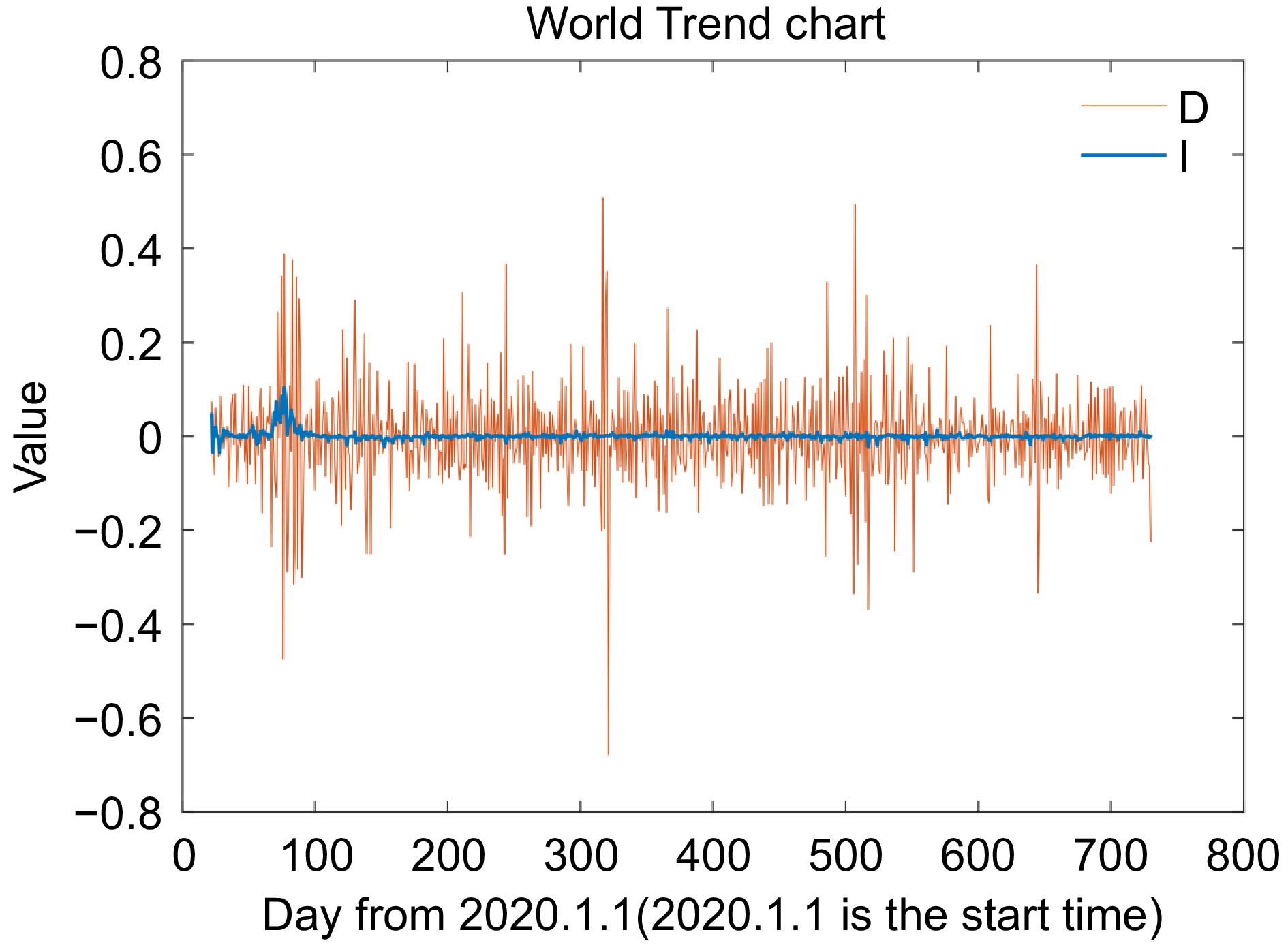
Figure 5.
Daily change of global severity index and service time of LNG carriers.
-
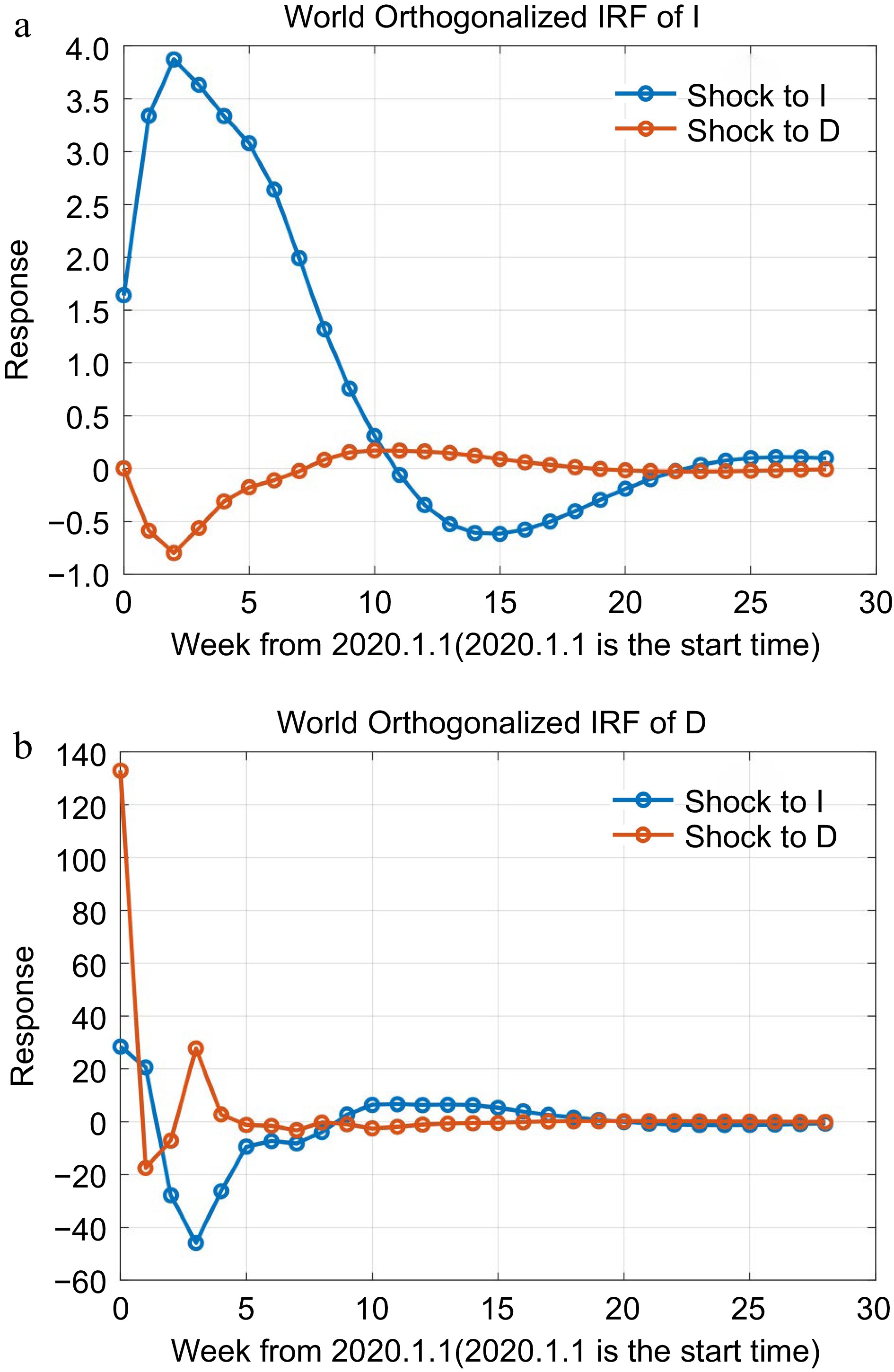
Figure 6.
Impulse response analysis of the global VAR (15) model.
-
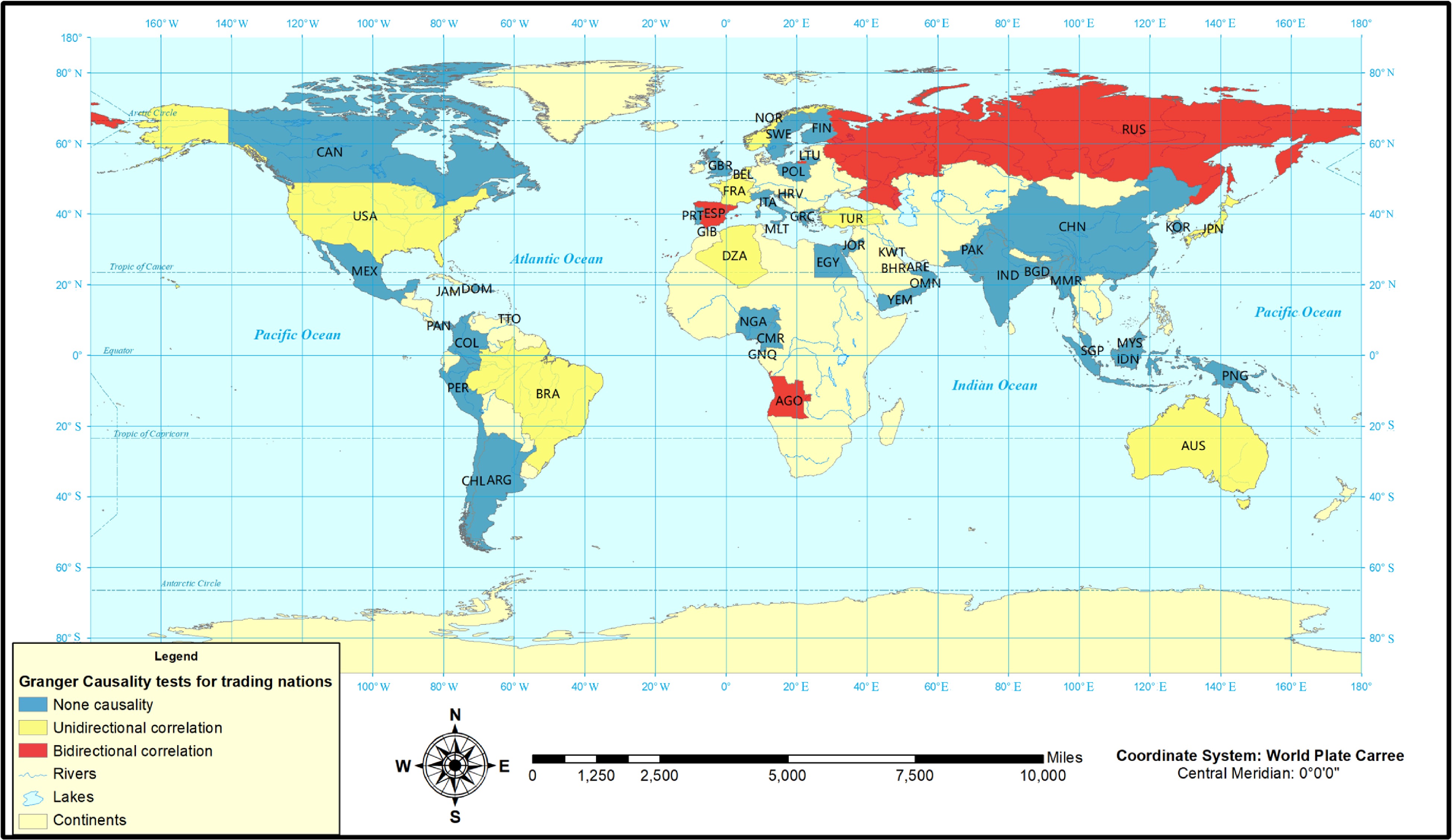
Figure 7.
The spatial distribution of impacts from COVID-19 in countries (the global map is from ArcMap World map).
-
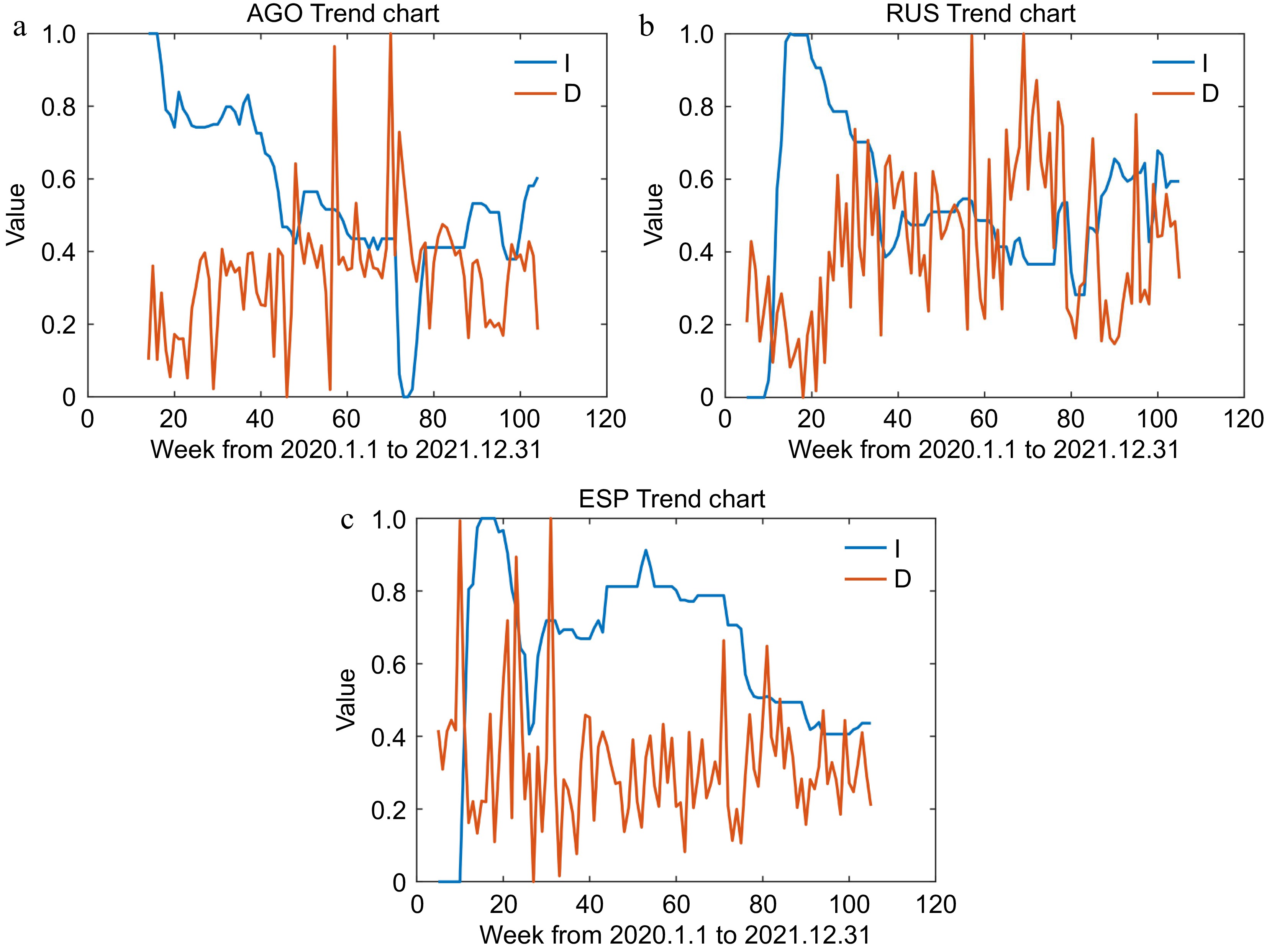
Figure 8.
LNG trade countries with bidirectional effects.
-
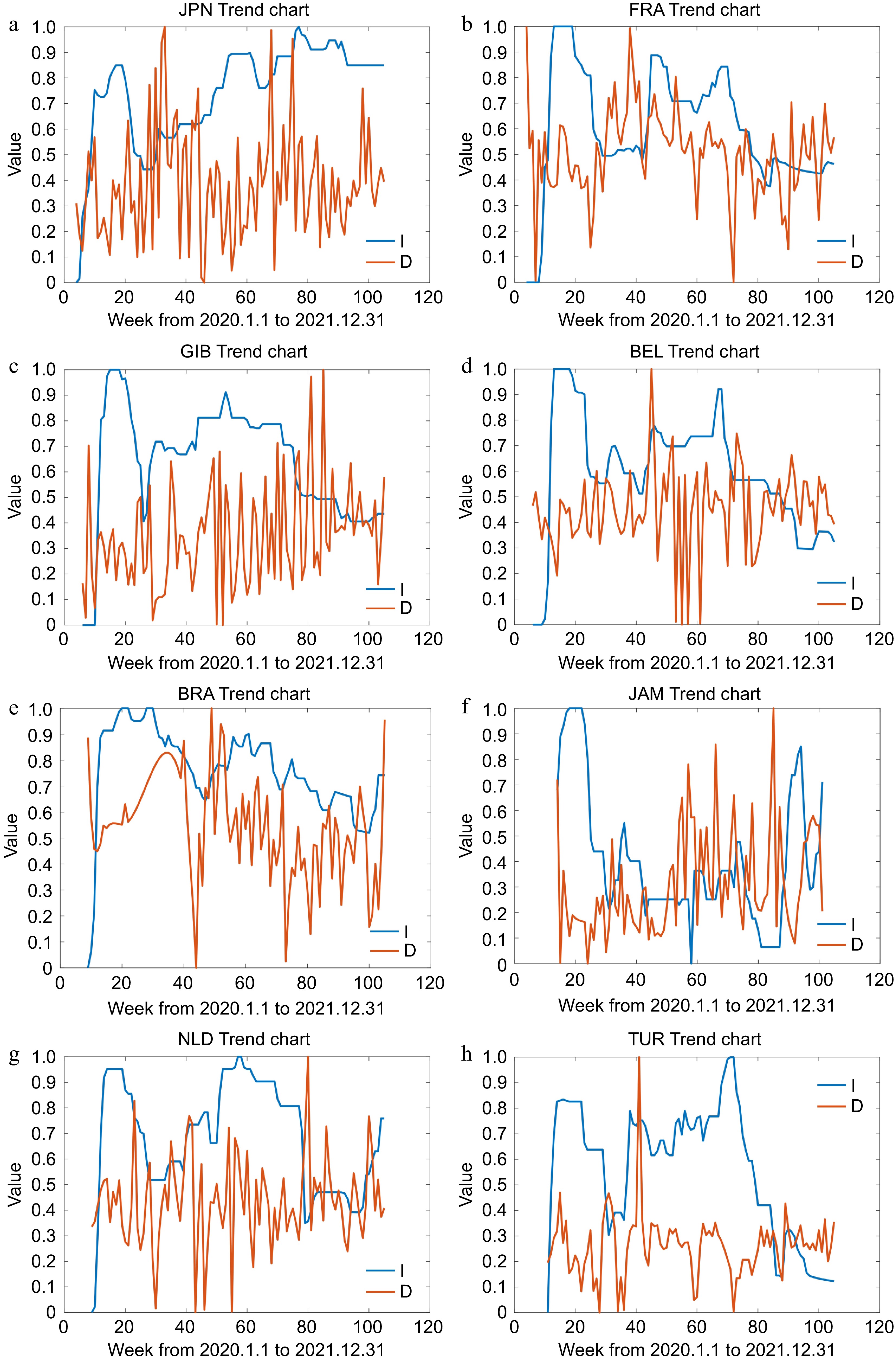
Figure 9.
LNG trade countries with the unidirectional effects.
-
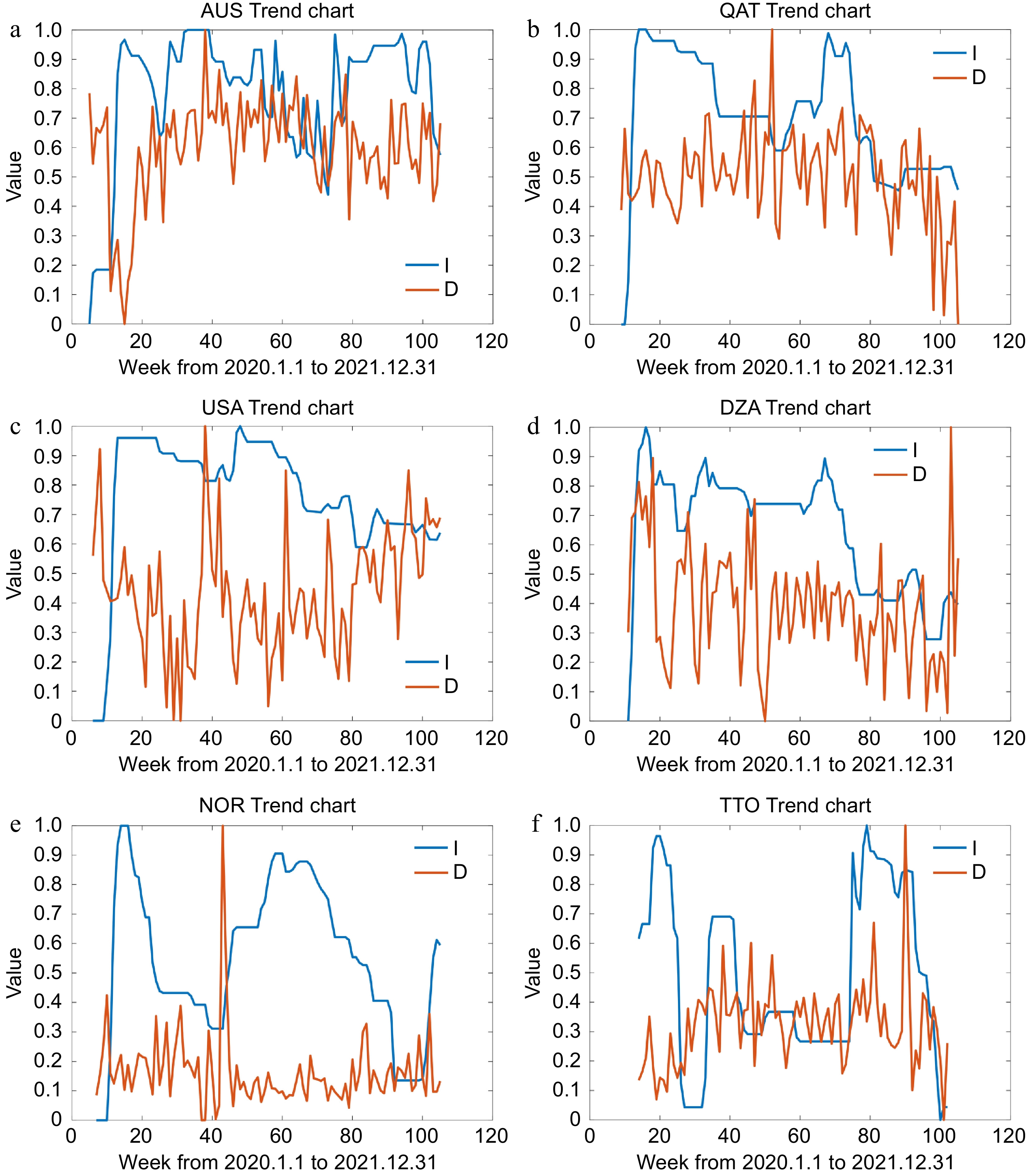
Figure 10.
LNG trade countries with the unidirectional effects.
-
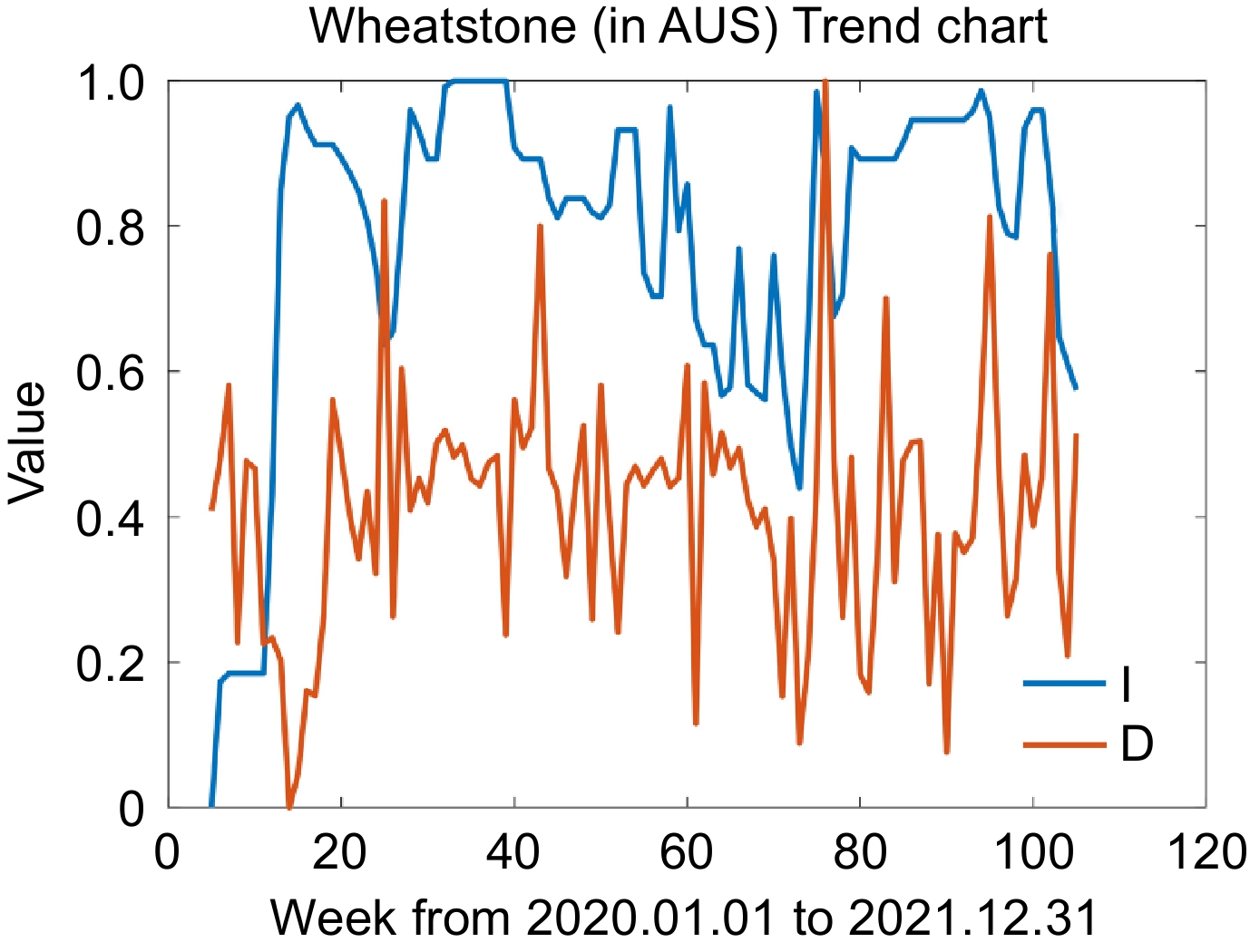
Figure 11.
LNG trade terminals with bidirectional effects.
-
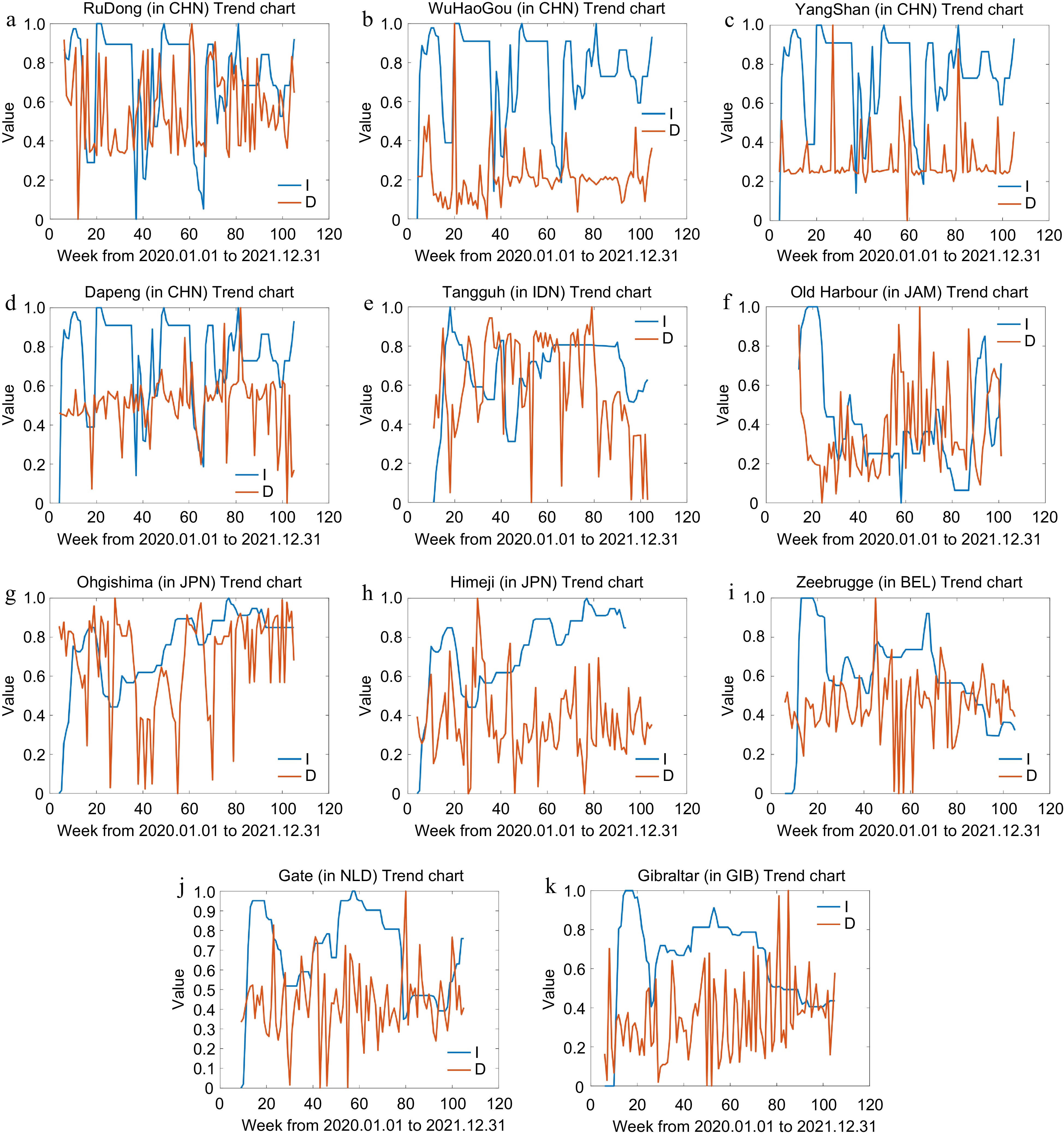
Figure 12.
LNG trade terminals with unidirectional effects.
-
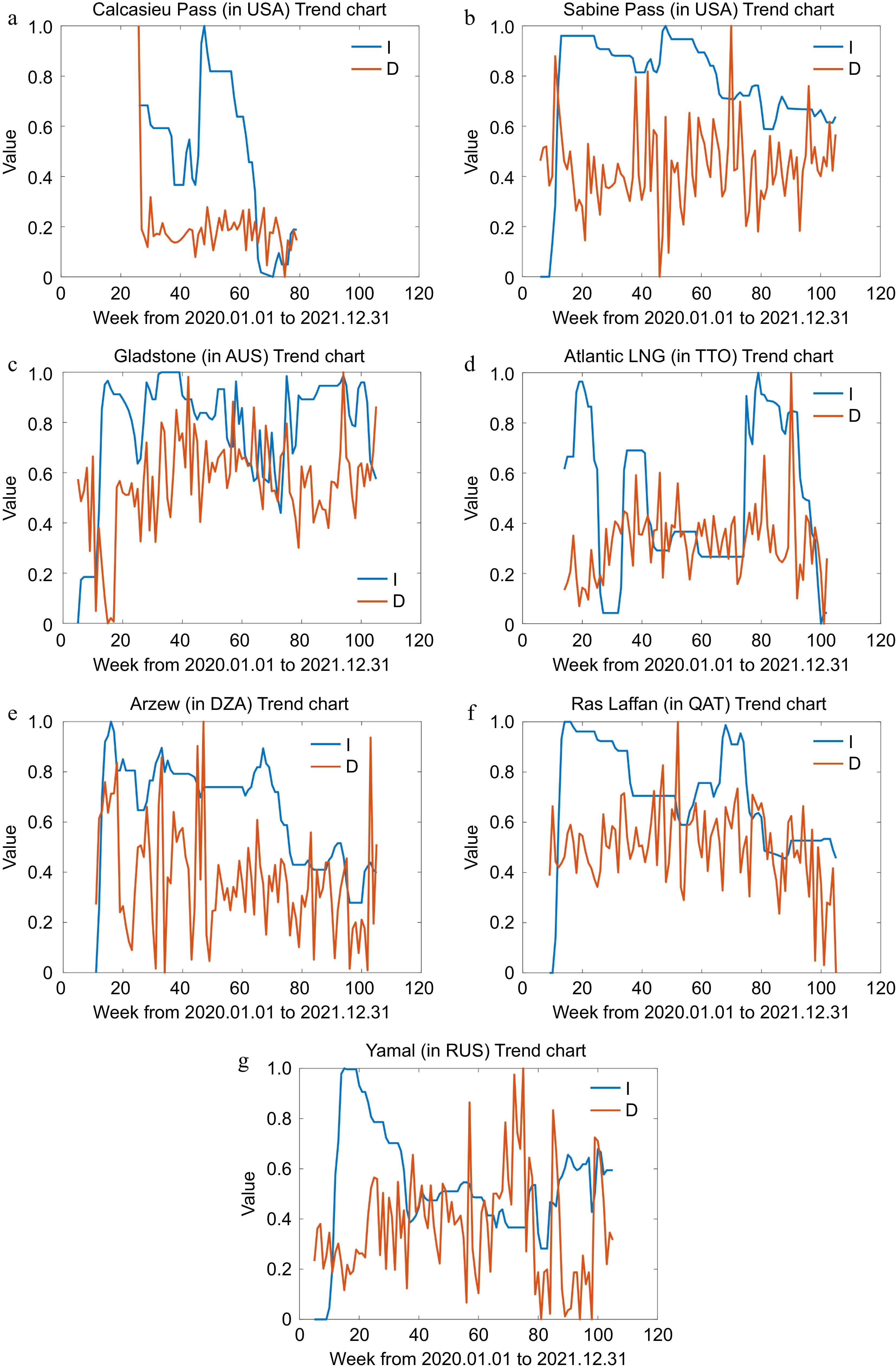
Figure 13.
LNG trade terminals with unidirectional effects.
-
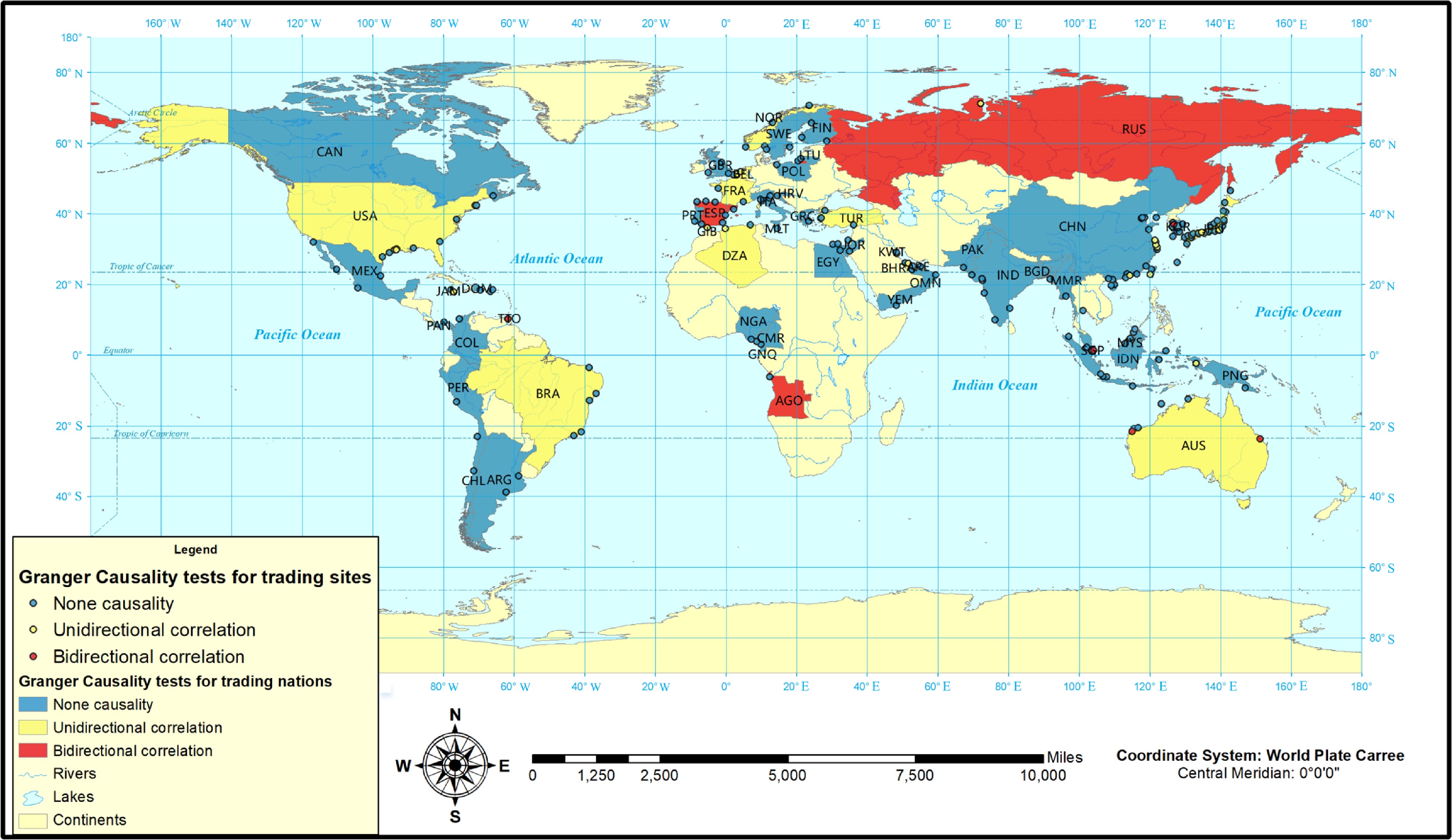
Figure 14.
The spatial distribution of impacts from COVID-19 in countries and LNG terminals (the global map is from ArcMap World map).
-
Reference Analytical method Specific method Hale & Angrist[1] Quantitative Quantitative indicators to assess the severity of the outbreak Wang et al.[15] Quantitative Dynamic time warping technique Dhaliwal et al.[25] Qualitative Closed questionnaire survey Zheng et al.[26] Quantitative Clustering algorithm Ihsan et al.[27] & Riess et al.[28] Qualitative Literature review and analysis March et al.[29], Xu et al.[30] &
Rožić et al.[34]Quantitative Data analysis/statistical methods Ge & Yang[31] Quantitative Comparative analysis, time series analysis, etc Dai & Liang[32] Quantitative Regression analysis Xu et al.[33] Quantitative Linear regression analysis Wan et al.[35] Quantitative analysis, combined with qualitative analysis Network analysis Dirzka & Acciaro[36] Quantitative analysis, combined with qualitative analysis Network analysis, time series analysis Table 1.
Analytical methods used in previous literature.
-
H0 Decision Distribution Statistic p-value Critical value Exclude lagged D in the I equation Reject H0 Chi-square Distribution 33.99 0.003416 24.996 Exclude lagged I in the D equation Reject H0 Chi-square Distribution 74.349 7.4223e-10 24.996 Table 2.
Granger causality test.
-
Countries VAR model No. p-value Angola (AGO) $\begin{aligned} \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}}\\ {\rm{y}}_{\rm{D},\rm{t}}\end{array}\right]=&\left[\begin{array}{c}0.0987\\ 0.4276\end{array}\right]+\left[\begin{array}{cc}1.2477& 0.0110\\ -0.1193& 0.1056\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-1}\\ {\rm{y}}_{\rm{D},\rm{t}-1}\end{array}\right]+\left[\begin{array}{cc}-0.3634& -0.1244\\ -0.1326& 0.0444\end{array}\right]\cdot \\&\left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-2}\\ {\rm{y}}_{\rm{D},\rm{t}-2}\end{array}\right]+\left[\begin{array}{c}{{\varepsilon }}_{\rm{I},\rm{t}}\\ {{\varepsilon }}_{\rm{D},\rm{t}}\end{array}\right] \end{aligned} $ (13) 0.045 Russia (RUS) $ \begin{aligned}\left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}}\\ {\rm{y}}_{\rm{D},\rm{t}}\end{array}\right]=&\left[\begin{array}{c}0.2243\\ 0.2598\end{array}\right]+\left[\begin{array}{cc}1.0696& -0.0328\\ 01282& 0.0914\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-1}\\ {\rm{y}}_{\rm{D},\rm{t}-1}\end{array}\right]+\left[\begin{array}{cc}-0.2360& -0.0221\\ -0.5976& 0.2035\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-2}\\ {\rm{y}}_{\rm{D},\rm{t}-2}\end{array}\right]+\\&\left[\begin{array}{cc}0.0602& -0.1326\\ -0.1697& 0.0690\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-3}\\ {\rm{y}}_{\rm{D},\rm{t}-3}\end{array}\right]+\left[\begin{array}{cc}-0.1371& -0.0140\\ 0.5124& 0.2163\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-4}\\ {\rm{y}}_{\rm{D},\rm{t}-4}\end{array}\right]+\left[\begin{array}{c}{\rm{\epsilon }}_{\rm{I},\rm{t}}\\ {\rm{\epsilon }}_{\rm{D},\rm{t}}\end{array}\right]\end{aligned}$ (14) 0.046 Spain (ESP) $\begin{aligned} \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}}\\ {\rm{y}}_{\rm{D},\rm{t}}\end{array}\right]=&\left[\begin{array}{c}0.0568\\ 0.2904\end{array}\right]+\left[\begin{array}{cc}1.1786& -0.0676\\ 0.2758& 0.1075\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-1}\\ {\rm{y}}_{\rm{D},\rm{t}-1}\end{array}\right]+\left[\begin{array}{cc}-0.2480& -0.0101\\ -0.8114& -0.0989\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-2}\\ {\rm{y}}_{\rm{D},\rm{t}-2}\end{array}\right]+\\&\left[\begin{array}{cc}0.0856& -0.0711\\ 1.6907& 0.1255\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-3}\\ {\rm{y}}_{\rm{D},\rm{t}-3}\end{array}\right]+\left[\begin{array}{cc}-0.0656& 0.0593\\ -1.1612& -0.0218\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-4}\\ {\rm{y}}_{\rm{D},\rm{t}-4}\end{array}\right]+\left[\begin{array}{c}{\rm{\epsilon }}_{\rm{I},\rm{t}}\\ {\rm{\epsilon }}_{\rm{D},\rm{t}}\end{array}\right]\end{aligned} $ (15) 0.039 Table 3.
VAR models for LNG trade countries with bidirectional effects.
-
Country VAR models No. p-value Japan (JPN) $ {\rm{y}}_{\rm{D},\rm{t}}=0.7089-0.3462{\rm{y}}_{\rm{I},\rm{t}-1}-0.0782{\rm{y}}_{\rm{D},\rm{t}-1}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (16) 0.045 France (FRA) $ {\rm{y}}_{\rm{D},\rm{t}}=0.2924+0.9373{\rm{y}}_{\rm{I},\rm{t}-1}+0.3880{\rm{y}}_{\rm{D},\rm{t}-1}-0.8978{\rm{y}}_{\rm{I},\rm{t}-2}-0.0189{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (17) 0.037 Gibraltar (GIB) $ {\rm{y}}_{\rm{D},\rm{t}}=0.6415-0.3850{\rm{y}}_{\rm{I},\rm{t}-1}-0.1292{\rm{y}}_{\rm{D},\rm{t}-1}+0.0845{\rm{y}}_{\rm{I},\rm{t}-2}-0.1165{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (18) 0.038 Belgium (BEL) $\begin{aligned} {\rm{y}}_{\rm{D},\rm{t}}=\;&0.5767+0.7123{\rm{y}}_{\rm{I},\rm{t}-1}-0.0269{\rm{y}}_{\rm{D},\rm{t}-1}-1.3813{\rm{y}}_{\rm{I},\rm{t}-2}+0.0881{\rm{y}}_{\rm{D},\rm{t}-2}+0.5651{\rm{y}}_{\rm{I},\rm{t}-3}-\\&0.1666{\rm{y}}_{\rm{D},\rm{t}-3}+{{\varepsilon }}_{\rm{D},\rm{t}}\end{aligned} $ (19) 0.016 Brazil (BRA) $ {\rm{y}}_{\rm{D},\rm{t}}=0.0366+0.3695{\rm{y}}_{\rm{I},\rm{t}-1}+0.4148{\rm{y}}_{\rm{D},\rm{t}-1}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (20) 0.030 Jamaica (JAM) $ {\rm{y}}_{\rm{D},\rm{t}}=0.2570-0.5282{\rm{y}}_{\rm{I},\rm{t}-1}+0.1874{\rm{y}}_{\rm{D},\rm{t}-1}+0.3536{\rm{y}}_{\rm{I},\rm{t}-2}+0.1969{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (21) 0.016 Netherlands (NLD) $ {\rm{y}}_{\rm{D},\rm{t}}=0.5710-0.8500{\rm{y}}_{\rm{I},\rm{t}-1}-0.0341{\rm{y}}_{\rm{D},\rm{t}-1}+0.7375{\rm{y}}_{\rm{I},\rm{t}-2}-0.0909{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (22) 0.042 The Republic of Turkey (TUR) $ \begin{aligned}{\rm{y}}_{\rm{D},\rm{t}}=\;&0.2526+0.0182{\rm{y}}_{\rm{I},\rm{t}-1}+0.3547{\rm{y}}_{\rm{D},\rm{t}-1}-0.4094{\rm{y}}_{\rm{I},\rm{t}-2}+0.0653{\rm{y}}_{\rm{D},\rm{t}-2}+0.9584{\rm{y}}_{\rm{I},\rm{t}-3}-\\&0.2432{\rm{y}}_{\rm{D},\rm{t}-3}-0.6571{\rm{y}}_{\rm{I},\rm{t}-4}+0.0492{\rm{y}}_{\rm{D},\rm{t}-4}+{{\varepsilon }}_{\rm{D},\rm{t}}\end{aligned} $ (23) 0.001 Table 4.
VAR models for LNG trade countries with unidirectional effects.
-
Country VAR models No. p-value Australia (AUS) $ \begin{aligned}{\rm{y}}_{\rm{D},\rm{t}}=\;&0.0022+0.0666{\rm{y}}_{\rm{I},\rm{t}-1}+0.2705{\rm{y}}_{\rm{D},\rm{t}-1}+0.0817{\rm{y}}_{\rm{I},\rm{t}-2}+0.1347{\rm{y}}_{\rm{D},\rm{t}-2}-0.1475{\rm{y}}_{\rm{I},\rm{t}-3}+\\&0.1131{\rm{y}}_{\rm{D},\rm{t}-3}+0.2427{\rm{y}}_{\rm{I},\rm{t}-4}+0.1534{\rm{y}}_{\rm{D},\rm{t}-4}+{{\varepsilon }}_{\rm{D},\rm{t}}\end{aligned} $ (24) 0.031 Qatar (QAT) $ \begin{aligned}{\rm{y}}_{\rm{D},\rm{t}}=\;&0.1406+1.0000{\rm{y}}_{\rm{I},\rm{t}-1}+0.1896{\rm{y}}_{\rm{D},\rm{t}-1}-1.5588{\rm{y}}_{\rm{I},\rm{t}-2}+0.0267{\rm{y}}_{\rm{D},\rm{t}-2}+\\&0.7354{\rm{y}}_{\rm{I},\rm{t}-3}+0.2484{\rm{y}}_{\rm{D},\rm{t}-3}+{{\varepsilon }}_{\rm{D},\rm{t}} \end{aligned}$ (25) 0.048 The United States of America (USA) $ {\rm{y}}_{\rm{D},\rm{t}}=0.7903-0.3672{\rm{y}}_{\rm{I},\rm{t}-1}+0.2552{\rm{y}}_{\rm{D},\rm{t}-1}-0.2243{\rm{y}}_{\rm{I},\rm{t}-2}-0.0257{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (26) 0.023 Algeria (DZA) $ {\rm{y}}_{\rm{D},\rm{t}}=0.0849+0.3148{\rm{y}}_{\rm{I},\rm{t}-1}+0.2820{\rm{y}}_{\rm{D},\rm{t}-1}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (27) 0.008 Norway (NOR) $ {\rm{y}}_{\rm{D},\rm{t}}=0.1928-0.0231{\rm{y}}_{\rm{I},\rm{t}-1}-0.0066{\rm{y}}_{\rm{D},\rm{t}-1}-0.0664{\rm{y}}_{\rm{I},\rm{t}-2}-0.0394{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (28) 0.041 Republic of Trinidad
and Tobago (TTO)$ {\rm{y}}_{\rm{D},\rm{t}}=0.3134+0.3438{\rm{y}}_{\rm{I},\rm{t}-1}+0.1425{\rm{y}}_{\rm{D},\rm{t}-1}-0.2941{\rm{y}}_{\rm{I},\rm{t}-2}-0.1221{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (29) 0.019 Table 5.
VAR models for LNG trade countries with unidirectional effects.
-
Country VAR models No. p-value Wheatstone (in AUS) $\begin{aligned} \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}}\\ {\rm{y}}_{\rm{D},\rm{t}}\end{array}\right]=\;&\left[\begin{array}{c}0.2149\\ 0.2195\end{array}\right]+\left[\begin{array}{cc}0.9943& -0.1503\\ 0.0583& 0.1290\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-1}\\ {\rm{y}}_{\rm{D},\rm{t}-1}\end{array}\right]+\left[\begin{array}{cc}-0.2033& -0.0349\\ -0.1242& 0.0727\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-2}\\ {\rm{y}}_{\rm{D},\rm{t}-2}\end{array}\right]+\\&\left[\begin{array}{cc}-0.2492& 0.0803\\ -0.5307& 0.0528\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-3}\\ {\rm{y}}_{\rm{D},\rm{t}-3}\end{array}\right]+\left[\begin{array}{cc}0.2894& -0.0732\\ 0.5183& -0.1099\end{array}\right]\cdot \left[\begin{array}{c}{\rm{y}}_{\rm{I},\rm{t}-4}\\ {\rm{y}}_{\rm{D},\rm{t}-4}\end{array}\right]+\left[\begin{array}{c}{{\varepsilon }}_{\rm{I},\rm{t}}\\ {{\varepsilon }}_{\rm{D},\rm{t}}\end{array}\right]\end{aligned} $ (30) 0.026 Table 6.
VAR models for LNG trade terminals with bidirectional effects.
-
Country VAR models No. p-value RuDong (CHN) $ {\rm{y}}_{\rm{D},\rm{t}}=-0.0044+0.2351{\rm{y}}_{\rm{I},\rm{t}-1}+0.1944{\rm{y}}_{\rm{D},\rm{t}-1}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (31) 0.036 WuHaoGou (CHN) $ {\rm{y}}_{\rm{D},\rm{t}}=0.1814+0.1611{\rm{y}}_{\rm{I},\rm{t}-1}+0.2823{\rm{y}}_{\rm{D},\rm{t}-1}-0.1776{\rm{y}}_{\rm{I},\rm{t}-2}-0.0726{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (32) 0.047 YangShan (CHN) $ {\rm{y}}_{\rm{D},\rm{t}}=0.3060+0.2477{\rm{y}}_{\rm{I},\rm{t}-1}-0.0487{\rm{y}}_{\rm{D},\rm{t}-1}-0.1985{\rm{y}}_{\rm{I},\rm{t}-2}-0.0873{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (33) 0.021 Dapeng (CHN) $ {\rm{y}}_{\rm{D},\rm{t}}=0.3496+0.1668{\rm{y}}_{\rm{I},\rm{t}-1}+0.0598{\rm{y}}_{\rm{D},\rm{t}-1}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (34) 0.025 Tangguh (IDN) $ {\rm{y}}_{\rm{D},\rm{t}}=-0.1925+0.7286{\rm{y}}_{\rm{I},\rm{t}-1}+0.3988{\rm{y}}_{\rm{D},\rm{t}-1}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (35) 0.035 Old Harbour (JAM) $ {\rm{y}}_{\rm{D},\rm{t}}=0.2729-0.6179{\rm{y}}_{\rm{I},\rm{t}-1}+0.2106{\rm{y}}_{\rm{D},\rm{t}-1}+0.4548{\rm{y}}_{\rm{I},\rm{t}-2}+0.1951{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (36) 0.017 Ohgishima (JPN) $ {\rm{y}}_{\rm{D},\rm{t}}=-0.0869-0.3893{\rm{y}}_{\rm{I},\rm{t}-1}+0.2866{\rm{y}}_{\rm{D},\rm{t}-1}+0.8705{\rm{y}}_{\rm{I},\rm{t}-2}+0.2662{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (37) 0.034 Himeji (JPN) $ {\rm{y}}_{\rm{D},\rm{t}}=0.4339+1.1299{\rm{y}}_{\rm{I},\rm{t}-1}+0.2915{\rm{y}}_{\rm{D},\rm{t}-1}-1.3366{\rm{y}}_{\rm{I},\rm{t}-2}-0.0446{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (38) 0.019 Zeebrugge (BEL) $ \begin{aligned}{\rm{y}}_{\rm{D},\rm{t}}=\;&0.5767+0.7123{\rm{y}}_{\rm{I},\rm{t}-1}-0.0269{\rm{y}}_{\rm{D},\rm{t}-1}-1.3813{\rm{y}}_{\rm{I},\rm{t}-2}+0.0881{\rm{y}}_{\rm{D},\rm{t}-2}+\\&0.5651{\rm{y}}_{\rm{I},\rm{t}-3}-0.1666{\rm{y}}_{\rm{D},\rm{t}-3}+{{\varepsilon }}_{\rm{D},\rm{t}}\end{aligned} $ (39) 0.016 Gate (NLD) $ {\rm{y}}_{\rm{D},\rm{t}}=0.5710-0.8500{\rm{y}}_{\rm{I},\rm{t}-1}-0.0341{\rm{y}}_{\rm{D},\rm{t}-1}+0.7375{\rm{y}}_{\rm{I},\rm{t}-2}-0.0909{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (40) 0.042 Gibraltar (GIB) $ {\rm{y}}_{\rm{D},\rm{t}}=0.6415-0.3850{\rm{y}}_{\rm{I},\rm{t}-1}-0.1292{\rm{y}}_{\rm{D},\rm{t}-1}+0.0845{\rm{y}}_{\rm{I},\rm{t}-2}-0.1165{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (41) 0.038 Table 7.
VAR models for LNG trade terminals with unidirectional effects.
-
Countries VAR model No. p-value Calcasieu Pass (USA) $ {\rm{y}}_{\rm{D},\rm{t}}=0.1810+0.0503{\rm{y}}_{\rm{I},\rm{t}-1}-0.213{\rm{y}}_{\rm{D},\rm{t}-1}+0.0290{\rm{y}}_{\rm{I},\rm{t}-2}-0.0348{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (42) 0.034 Sabine Pass (USA) $ {\rm{y}}_{\rm{D},\rm{t}}=0.6854+0.2954{\rm{y}}_{\rm{I},\rm{t}-1}+0.0383{\rm{y}}_{\rm{D},\rm{t}-1}-0.5424{\rm{y}}_{\rm{I},\rm{t}-2}-0.1727{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (43)
0.003Gladstone (AUS) $\begin{aligned} {\rm{y}}_{\rm{D},\rm{t}}=\;&0.1265-0.0496{\rm{y}}_{\rm{I},\rm{t}-1}+0.2311{\rm{y}}_{\rm{D},\rm{t}-1}-0.1505{\rm{y}}_{\rm{I},\rm{t}-2}+0.2017{\rm{y}}_{\rm{D},\rm{t}-2}-0.0681{\rm{y}}_{\rm{I},\rm{t}-3}+\\&0.0441{\rm{y}}_{\rm{D},\rm{t}-3}+0.4782{\rm{y}}_{\rm{I},\rm{t}-4}+0.0114{\rm{y}}_{\rm{D},\rm{t}-4}+{{\varepsilon }}_{\rm{D},\rm{t}} \end{aligned}$ (44) 0.001 Atlantic LNG (TTO) $ {\rm{y}}_{\rm{D},\rm{t}}=0.3134+0.3438{\rm{y}}_{\rm{I},\rm{t}-1}+0.1425{\rm{y}}_{\rm{D},\rm{t}-1}-0.2941{\rm{y}}_{\rm{I},\rm{t}-2}-0.1221{\rm{y}}_{\rm{D},\rm{t}-2}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (45) 0.003 Arzew (DZA) $ {\rm{y}}_{\rm{D},\rm{t}}=0.1302+0.3213{\rm{y}}_{\rm{I},\rm{t}-1}+0.0516{\rm{y}}_{\rm{D},\rm{t}-1}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (46) 0.094 Ras Laffan (QAT) $ \begin{aligned}{\rm{y}}_{\rm{D},\rm{t}}=\;&0.1406+1.0000{\rm{y}}_{\rm{I},\rm{t}-1}+0.1896{\rm{y}}_{\rm{D},\rm{t}-1}-1.5588{\rm{y}}_{\rm{I},\rm{t}-2}+0.0267{\rm{y}}_{\rm{D},\rm{t}-2}+\\&0.7354{\rm{y}}_{\rm{I},\rm{t}-3}+0.2484{\rm{y}}_{\rm{D},\rm{t}-3}+{{\varepsilon }}_{\rm{D},\rm{t}} \end{aligned}$ (47) 0.048 Yamal (RUS) $ {\rm{y}}_{\rm{D},\rm{t}}=0.3903-0.24120{\rm{y}}_{\rm{I},\rm{t}-1}+0.3309{\rm{y}}_{\rm{D},\rm{t}-1}+{{\varepsilon }}_{\rm{D},\rm{t}} $ (48) 0.050 Table 8.
VAR models for LNG trade terminals with unidirectional effects.
Figures
(14)
Tables
(8)