-
Airline scheduling in the civil aviation industry is very complex. It usually starts a few months in advance and involves millions of flights. In the past few decades, optimization research on airline scheduling has obtained rich results[1,2], especially in the field of operations research.
However, the daily operations of the original airline schedules are often disrupted by internal or external factors, such as severe weather, crew reassignments, and maintenance problems. These disruptions may result in great economic damage and damage to the reputations of airlines. It is impossible to completely eliminate the losses caused by these disruptions. Currently, a common recovery method is to reschedule resources, such as aircraft, crews, and passengers, to bring the flight schedules back to the original situation as quickly as possible and minimize the losses caused by the disruptions. This strategy is defined as airline disruption management[3].
In recent years, the factors causing disruptions have become increasingly complex. As individual awareness has grown, disruptions due to strikes or staff shortages have become more frequent. The integration of smart aviation means more technological applications, but it has also brought a higher risk of large-scale flight disruptions. The frequency and scale of flight interruptions are both on the rise. Therefore, it is always a challenge to obtain efficient solutions for airline disruption management for both the civil aviation industry and operations research scholars.
Previous research and motivation
-
Since the study of airline schedule recovery began with Teodorović & Guberinić[4], it has been a topic of concern for an increasing number of researchers. Etschmaier & Mathaisel[5] introduce an overview of airline scheduling from the perspective of operations research over the previous 20 years and points out the necessity of future research on airline schedule recovery. At the end of the 20th century and the beginning of the 21st century, airline recovery research grew explosively. and classic models and methodologies of aircraft recovery and crew recovery were proposed by scholars such as Yan, Clarke, Bard and Yu.
The formal definition of airline disruption management was not given until Yu & Qi[3]. They[3] point out that airline disruption management mainly refers to the recovery of two airline resources: aircraft and crew. It also systematically constructs a network of aircraft and crew recovery. However, there are only a few reviews of the airline disruption management problem from the perspective of operations research.
Ball et al.[6] explicitly describe three aspects of airline schedule recovery: aircraft recovery, crew recovery, and passenger recovery. Moreover, they give a classic model formulation of the recovery of each resource. Kohl et al.[7] not only give a detailed introduction to various aspects of airline disruption management but also use actual project experience with airline disruption management. This is the first review paper that proposes including passenger itinerary recovery in airline disruption management. Clausen et al.[8] provide a detailed overview of the network for airline schedules. This confirms that the solution methodology used for airline disruption management is similar to that used for airline schedule planning. Moreover, it introduces a thorough review of airline disruption management with the resources of aircraft, crews, passengers and integrated recovery. Artigues et al.[9] discuss the ROADEF 2008/2009 Challenge, an international competition organized by the French Operational Research and Decision Support Society (ROADEF). This challenge presents an airline disruption management problem, i.e., recovering flight planning, aircraft assignments, crew, and passenger itineraries in a given period under one or more airline disruptions. It first introduces the detailed problem posed by this challenge, then reviews the most common solution methodologies applied in the challenge, and finally compares the solution results among nine different teams entering the final round. The review gives one important instance of airline disruption management applied to practical industry. The publication of challenge data has promoted a large number of research papers focusing on airline integrated recovery in subsequent years. Visentini et al.[10] define the airline schedule recovery problem as a real-time vehicle schedule recovery problem (RTVSRP) and categorize related literature according to the disruption types given by Bisaillon et al.[11]. Hassan et al.[12] provided a review of airline disruption management between 2009 and 2018. However, no comparison is illustrated with Clausen et al.[8]. The robustness of recovery strategies is also an important factor.
Research contributions
-
(1) A statistical analysis and comparison between two periods. Based on the collected papers from the period 2010-2024, a statistical analysis of the journal and field distribution, the types of recovery resources, the trend in the number of studies by year, and disruption types and recovery options are provided. Moreover, comparisons are drawn between the selected papers and the literature in Clausen et al.[8].
(2) A classification of integrated recovery based on a combination of recovery resources. In previous review papers, the airline disruption management problem has included the aircraft recovery problem, crew recovery problem, and integrated recovery problem. The integrated recovery problem is further divided into integrated recovery of aircraft and crew, integrated recovery of aircraft and passengers, and integrated recovery of total resources.
(3) An identification of research directions. Conclusions from the current literature are drawn and then future research directions identified in three areas: problems, models, and solution methods for airline disruption management. We intend to work in some of the research directions in this field. We also hope that other scholars will work in this field so that collectively, our research can promote achievements in the theory, methodology, and technology of airline disruption management.
Organization of the paper
-
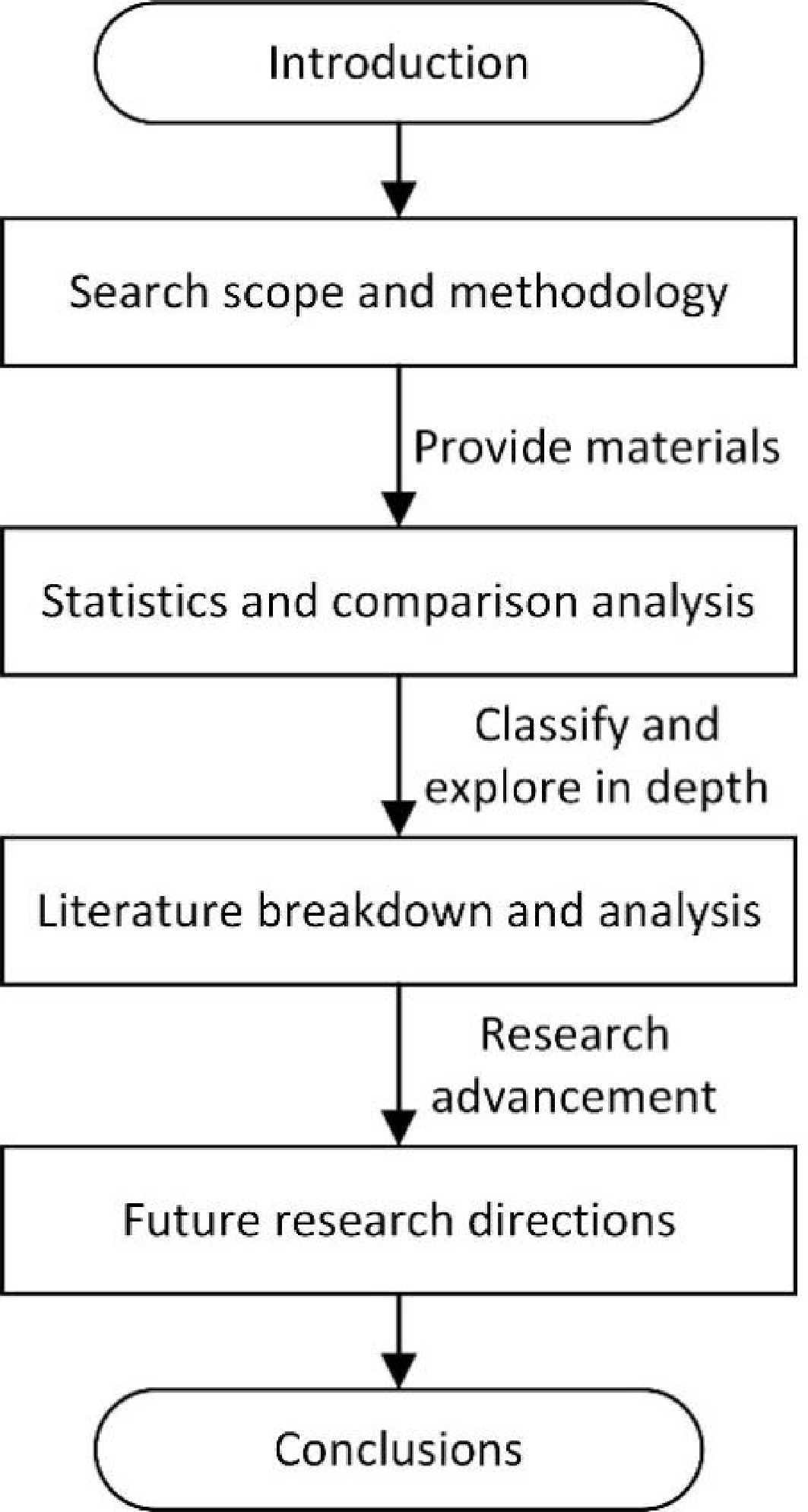
The remaining content of the paper is organized as follows: In the next section, we define of airline disruption management and the search range of the collected literature. This is followed by a statistical analysis that is compared with that of Clausen et al.[8]. Detailed information and corresponding research findings in the literature related to aircraft, crew, and integrated recovery are presented next. Future research directions in the three areas of problems, models, and solution methods are presented in the following section. Finally, conclusions are drawn. Research contents and the relationship between each section are shown in Fig. 1.
-
Currently, there is no unified and clear definition of disruption management in the academic field. However, most scholars have reached a common view. According to Yu & Qi[3], disruption management is a methodology that addresses disruptions in real-time. At the beginning of a business cycle, an optimal or near-optimal operational plan is obtained by using certain optimization models and solution schemes. When such an operational plan is executed, disruptions may occur from time to time that are caused by internal and external uncertain factors. As a result, the original operational plan may not remain optimal or even feasible. Consequently, we need to dynamically revise the original plan and obtain a new plan that reflects the constraints and objectives of the evolved environment while minimizing the negative impact of the disruption. Clausen et al.[8] limit disruption management to the basic goal of returning to the original plan as soon as possible to minimize system disturbance.
Although disruption management is currently not applied to the airline industry alone, the definition of disruption management indeed began with airline civil aviation. According to Yu & Qi[3], airline disruption management refers to disruption management for applications in airline operations. Airline disruption management is commonly implemented by an airline operation center (AOC). When a disruption occurs, the airline first needs to assess the disruption and then make revisions to their flight planning and the schedules of related resources.
In Yu & Qi[3], the recovery resources primarily include the aircraft and crew. Clausen et al.[8] report that passenger itineraries have also been included in recovery resources since Lettovsky[13] and Bratu & Barnhart[14]. Therefore, airline disruption management currently involves aircraft, crew, and integrated recovery of three resources, including passenger itineraries.
Aircraft recovery problem: When flight schedules are disrupted, the problem tries to minimize the division from the original schedules in terms of aircraft and flight operations. Generally, where some aircraft can be rerouted (aircraft swap), some disrupted flights can be given a new departure and arrival time (flight delay), and some disrupted flights can be cancelled (flight cancellation).
Crew recovery problem: when the flight schedules are recovered, the problem attempts to make a crew rescheduling decision to minimize the division related to crew schedules. Sometimes, flights can be delayed or cancelled as well.
Integrated recovery problem: During the recovery process, the problem aims to consider two or three recovery problems, such as aircraft recovery, crew recovery, and passenger itinerary recovery, in an integrated model.
Search methodology
-
After understanding the core concepts of airline disruption management, we focused on the task of finding published journal papers related to airline disruption management. To do this, a systematic approach was used, as described in what follows. The search began with the databases of ISI's Web of Science, ScienceDirect, and the Wiley Online Library. The keywords 'airline', 'aircraft', 'crew', and 'passenger' combined with 'perturbance', 'disruption', 'disrupted', 'irregular', 'recovery', 'rerouting', 'cancellation', 'delay', 'rescheduling', and 'reassignment' were searched in the titles of journal papers published in English. Book chapters and working papers were excluded. The period of the search was limited to 2008 and thereafter. To be more precise, if a journal paper related to the present topic was included in Clausen et al.[8], it was excluded from the present study. Therefore, most of the papers were published between 2010 and 2024.
After searching for the defined keywords in the mentioned journals, 1384 papers were obtained as the initial results. We were certain that many of these papers would not fit within the project scope. Hence, we continued extracting the papers most related to the topic of airline disruption management.
The titles and abstracts of the papers were checked and papers eliminated with titles completely different from the present research domain. For example, papers with titles or abstracts related to disruption management in railway transportation, public transportation, vehicle routing problems, and aircraft manufacturing were eliminted. Some papers focusing on airline delay prediction, delay propagation, airline gate assignment, air traffic flow management, and airport terminal optimization phases were also filtered out. By applying the above filters, 69 papers were identified for the present survey.
-
Statistical analysis and comparison of the published literature is now provided between 2010 and 2024, and before 2010. The papers published before 2010 are derived from Clausen et al.[8]. The characteristics of these papers are analyzed, namely, the journal and field distribution, the types of related resources, and the trend in the number of studies by year.
Journal and field distribution
-
The 69 selected papers were published in 29 journals and three types of conference proceedings after 2010. The statistical results from Clausen et al.[8] are provided for comparison. There were a total of 18 journals and five types of conference proceedings before 2010. This illustrates that the articles published after 2010 involve more journals than those published before 2010. This shows that there have been more journals focusing on airline disruption management problems in recent decades. There were more choices of journals for article publication after 2010 than before 2010.
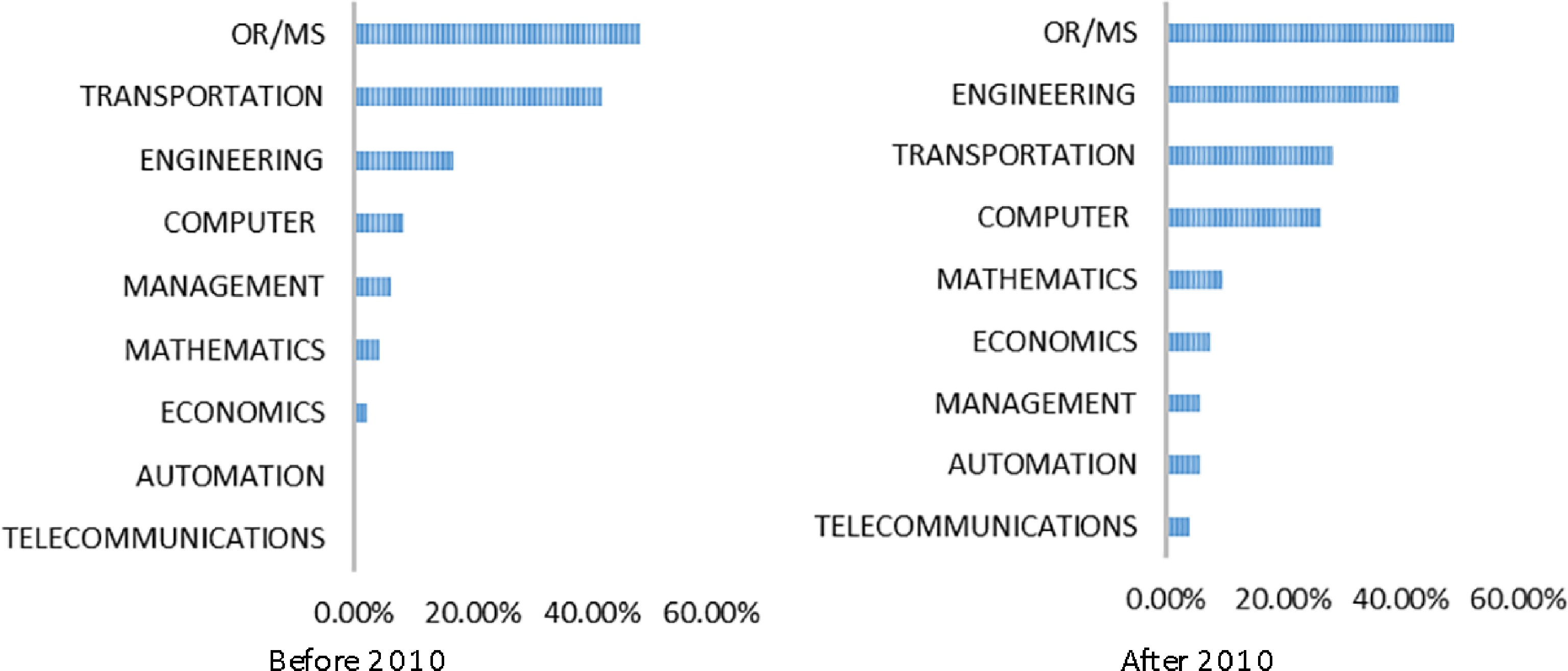
Based on the category lists on the InCites Journal Citations Report website[15], the numbers of published articles in various categories were statistically compared during both periods. Figure 2 shows the statistical results, where the vertical axis represents the research field and the horizontal axis represents the literature rate in each field, i.e., the number of published articles in the corresponding field divided by the total number of articles. The left graph in Fig. 2 corresponds to the period before 2010, and the right graph refers to the period after 2010. As we can see in Fig. 2, there are eight fields related to airline disruption management. 'OR/MS' refers to the category of 'OPERATIONS RESEARCH & MANAGEMENT SCIENCE' on the website[15]; 'TRANSPORTATION' includes both 'TRANSPORTATION' and 'TRANSPORTATION SCIENCE & TECHNOLOGY'; and 'ENGINEERING' is a collective name for the 'INDUSTRIAL', 'ELECTRICAL & ELECTRONIC', 'CIVIL', and 'MULTIDISCIPLINARY' areas. As some journals belong to more than one category, the papers published in the corresponding journals contribute to more than one research field. By comparing the two graphs in Fig. 2, we can easily find the differences between the two periods. First, six fields were involved before 2010, while eight fields were involved after 2010. Second, most studies before 2010 were published in journals in two research fields, while the range after 2010 extended to four research fields: 'OR/MS', 'ENGINEERING', 'TRANSPORTATION' and 'COMPUTER'. It is noted that the research field 'ENGINEERING' has concentrated more on this area than 'TRANSPORTATION'. This clearly illustrates that studies of airline disruption management problems have gained more influence, especially in the 'ENGINEERING' and 'COMPUTER' research fields.
Statistics on various resources of airline operations
-
Clausen et al.[8] collected and analyzed 48 studies on all types of airline disruption management problems from journal papers, conference proceedings, working papers, and technical reports, while we found 53 published papers among only journal papers and conference proceedings in the databases of ISI's Web of Science, ScienceDirect, and the Wiley Online Library. This shows that the total number of studies on airline disruption management problem has increased. We will display and compare the statistical results based on different resources in airline recovery.
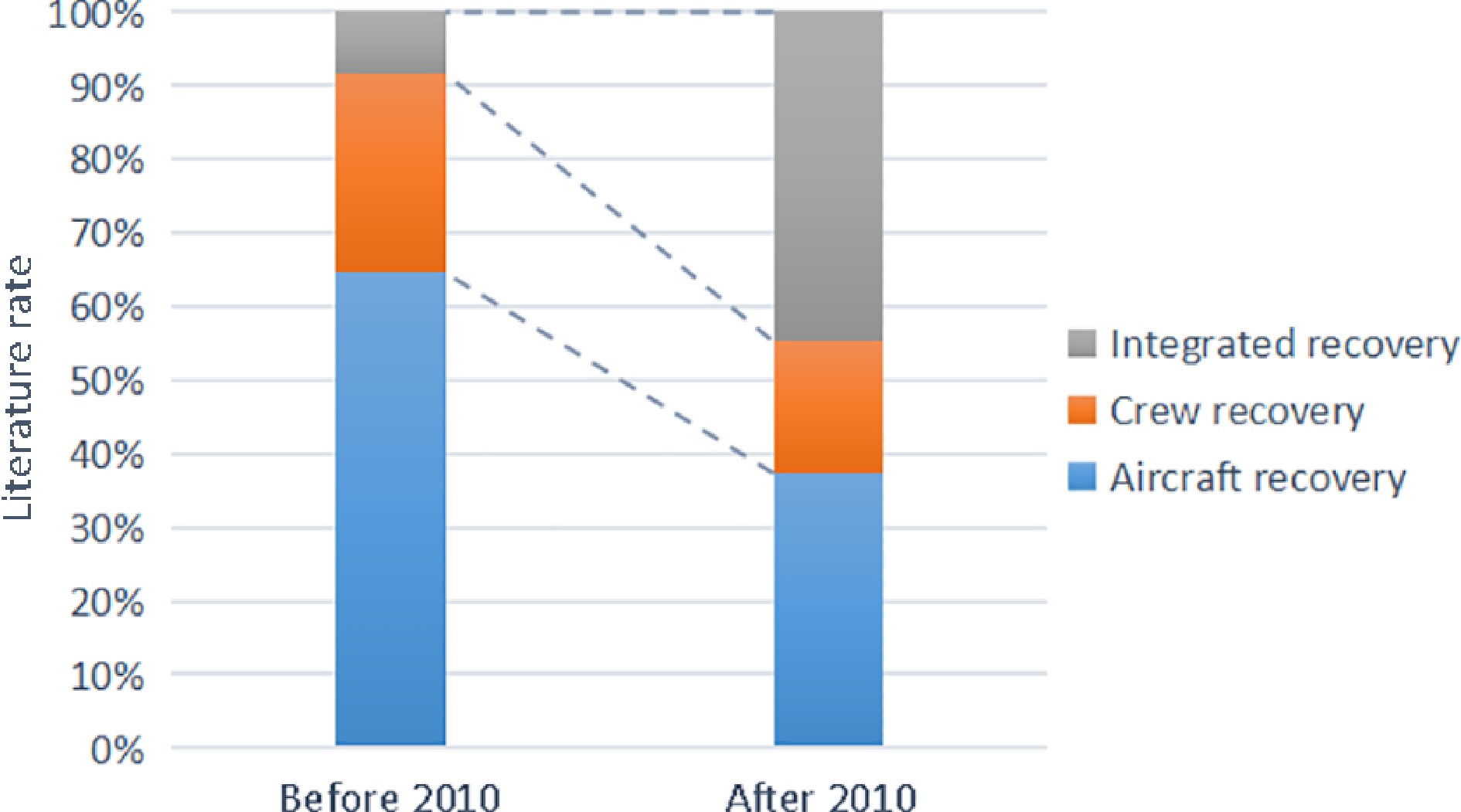
Generally, airline disruption management is related to three types of resources: aircraft, crew, and passengers. Passengers are special because they are also the object of airline service. Clausen et al.[8] and most studies divide the literature into three sets according to the related recovery resources. The three sets refer to three research topics: aircraft recovery, crew recovery, and integrated recovery. We also provide simple literature statistics on the three topics and compare them with those of Clausen et al.[8] in Fig. 3. The vertical axis represents the literature rates of the three topics.
As can be seen in Fig. 3, before 2010, more than 60% of papers focus on aircraft recovery, and less than 10% of papers concentrate on integrated recovery. After 2010, the rate of papers on integrated recovery increased to more than 40%, which is almost the same as that of aircraft recovery. Integrated recovery involves multiple resources during airline disruption recovery, and the complexity of the studies is far greater than that of single-resource recovery. Therefore, there are two reasons why integrated recovery after 2010 is more popular than before 2010. The first reason may be due to practical airline demands. Passengers are not only the service objects of airlines but also the main source of profits for airlines. Therefore, the primary purpose of airline disruption recovery is to deliver passengers to their destinations with suitable aircraft and crews. Approximately 90% of studies include passenger recovery in the research set of integrated recovery. The second reason may be due to the recent development of computer hardware and software technology. The computing efficiency is greatly improved, and it can meet the complex computing requirements of integrated recovery.
Trends in the number of studies by year and type of recovery resources
-
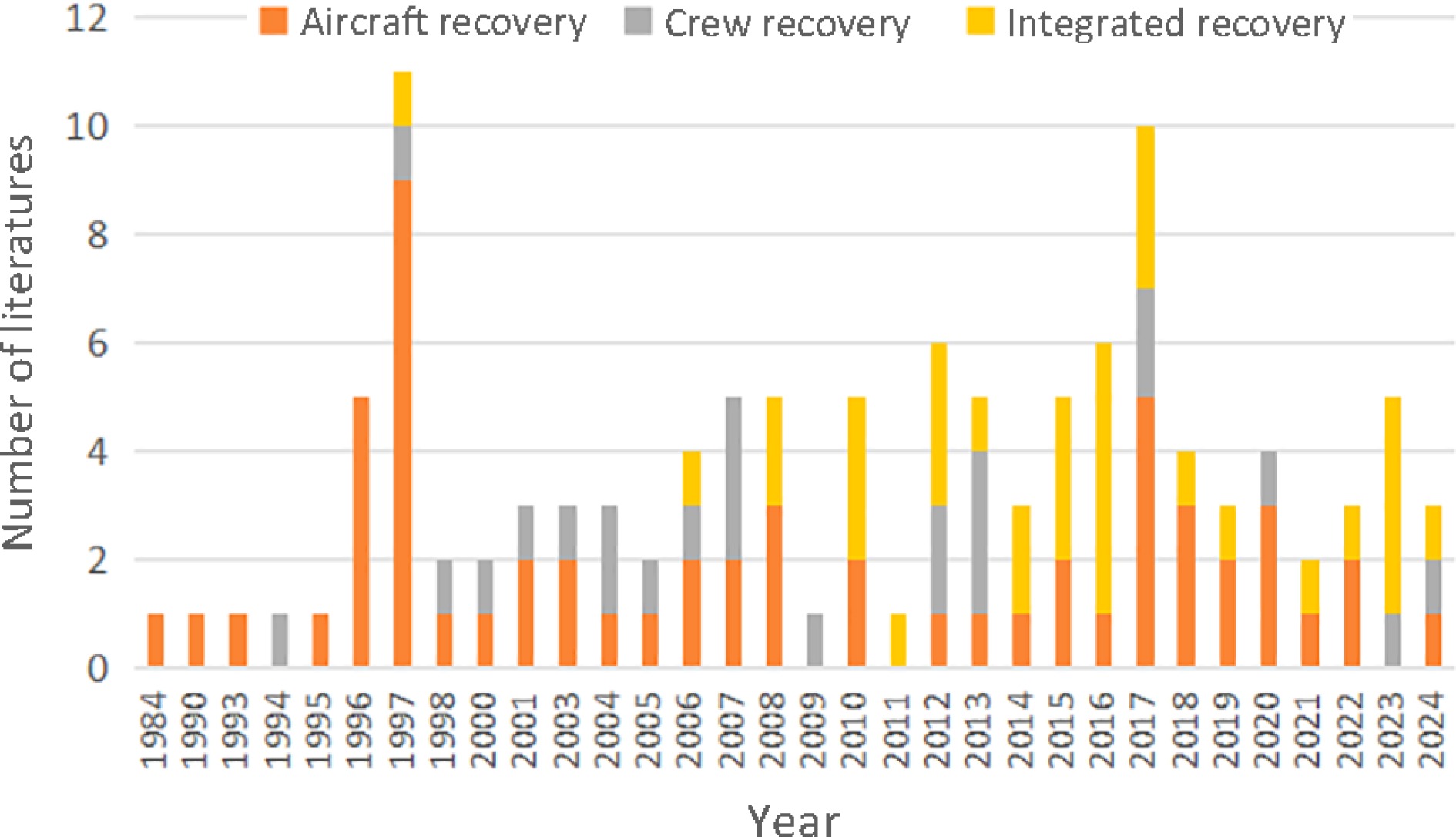
Figure 4 provides information about the number of studies during the years 1984−2024 and the types of recovery resources considered by these papers.
Figure 4 shows that the number of studies peaks in two years: 1997 and 2017. The trends can be divided into four segments by the two peaks. First, during the almost 12 years from 1984 to 1995, there were only five papers in four journals and one technical report. Second, in 1996 and 1997, the number of papers reached a peak of 16 papers. Two research groups led by Yan and Yu contributed nine papers to this peak. Then, between 1998 and 2005, the number of published papers was only two or three each year. Finally, between 2006 and 2019, except for 2017, the number of papers fluctuated greatly, with an average number of four or five per year. Since this time, on average, there has been a significant upward trend in the number of papers on airline disruption management recovery. Note that 2017 is the year with the largest number of published papers, 20 years after the previous peak. This shows an increase in researchers' attention to the area of airline disruption management in recent years.
Next, the trends of the research topic of resource recovery are the focus. (1) Aircraft recovery was the initial focus of airline disruption management in Teodorović & Guberinić[4]. It is interesting that there were only three published papers during the 10 years from 1984 to 1993. The number of papers increased explosively in 1997 and then largely stabilized at one or two per year. During the last three years, since 2017, the number of papers each year has increased to an average of three. (2) The research on crew recovery started in 1994 and maintained an average annual publication rate of one paper between 1997 and 2013. After 2014, the number of crew recovery publications clearly decreased. (3) In terms of integrated recovery, we can see in Fig. 4 that there are almost no publications before 2005, except for one Ph.D. thesis[13]. After 2006, however, the studies increased year by year and reached a peak in 2016. This shows that integrated recovery has attracted more scholars' attention in recent decades.
Statistics on disruptions and recovery options of airline operations
-
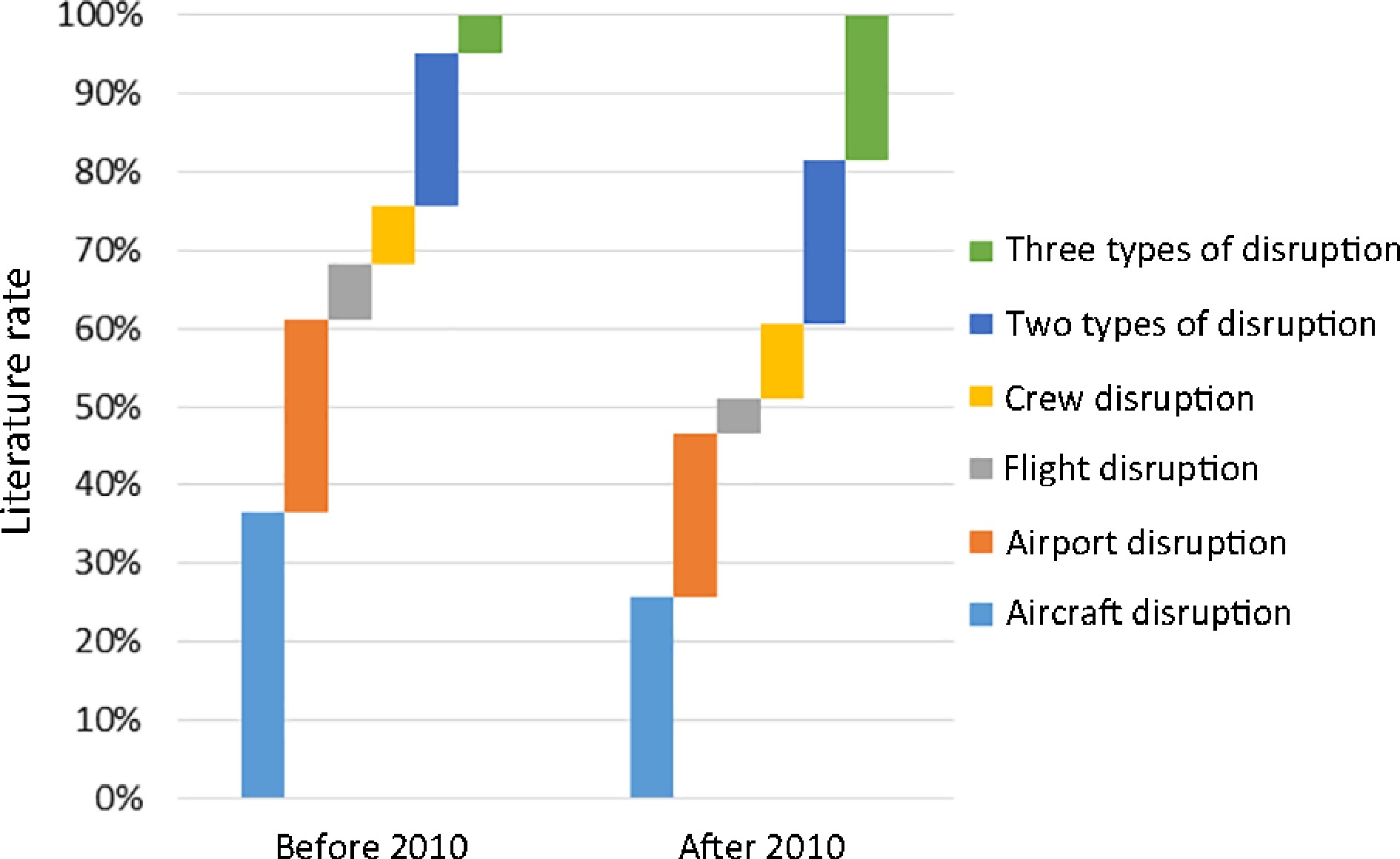
Airline schedules are often disrupted by internal or external factors, such as breakdown maintenance, severe weather, crew reassignments, and air traffic control. It will result in the shortage of some resources, such as aircraft, airports, crews, flights, and even simultaneous disruption of multiple resources, over a period of time. Figure 5 shows the comparison of disruption types considered by these papers before 2010 and after 2010. The vertical axis represents the literature rates of various disruption types. 'Aircraft disruption' refers to the literature that studies airline recovery under a shortage of aircraft for original schedules by a period of time due to breakdown maintenance or ground delay programs for air traffic control. 'Airport disruption' represents the papers that study airline recovery under airport closure for a period, often resulting from severe weather. 'Flight disruption' mainly refers to studies focusing on recovery under delay and cancellation of several flights. 'Crew disruption' mainly includes airline recovery studies under crew misconnection due to their late arrival, insufficient rest, crew duty exceeding, crew unassignment, and crew augmentation. Additionally, 'two types of disruption' and 'three types of disruption' refer to the problems where two and three types of resources are disrupted simultaneously and are considered in the paper.
From Fig. 5, we know that approximately 75% of papers focused on the recovery problem under a single type of disruption before 2010, while the rate of these papers decreased to less than 60% after 2010. In detail, the rates of papers focusing on 'aircraft disruption', 'airport disruption', and 'flight disruption' have decreased. However, more studies have focused on the recovery problem under multiple types of disruptions after 2010. It is the most obvious that the rate of the 'three types of disruption' apparently increased from less than 5% before 2010 to almost 20% after 2010. It is noted that the rates of 'two types of disruption' are almost the same before and after 2010, as shown in Fig. 5. Interestingly, we found that more papers studied the recovery problem under aircraft and flight disruption before 2010, but more papers focused on the recovery problem under aircraft and airport disruption after 2010. It is obvious that 'airport disruption' is much more complicated than 'flight disruption'. Overall, we can conclude from disruption types that airline disruption management is more complicated than before.
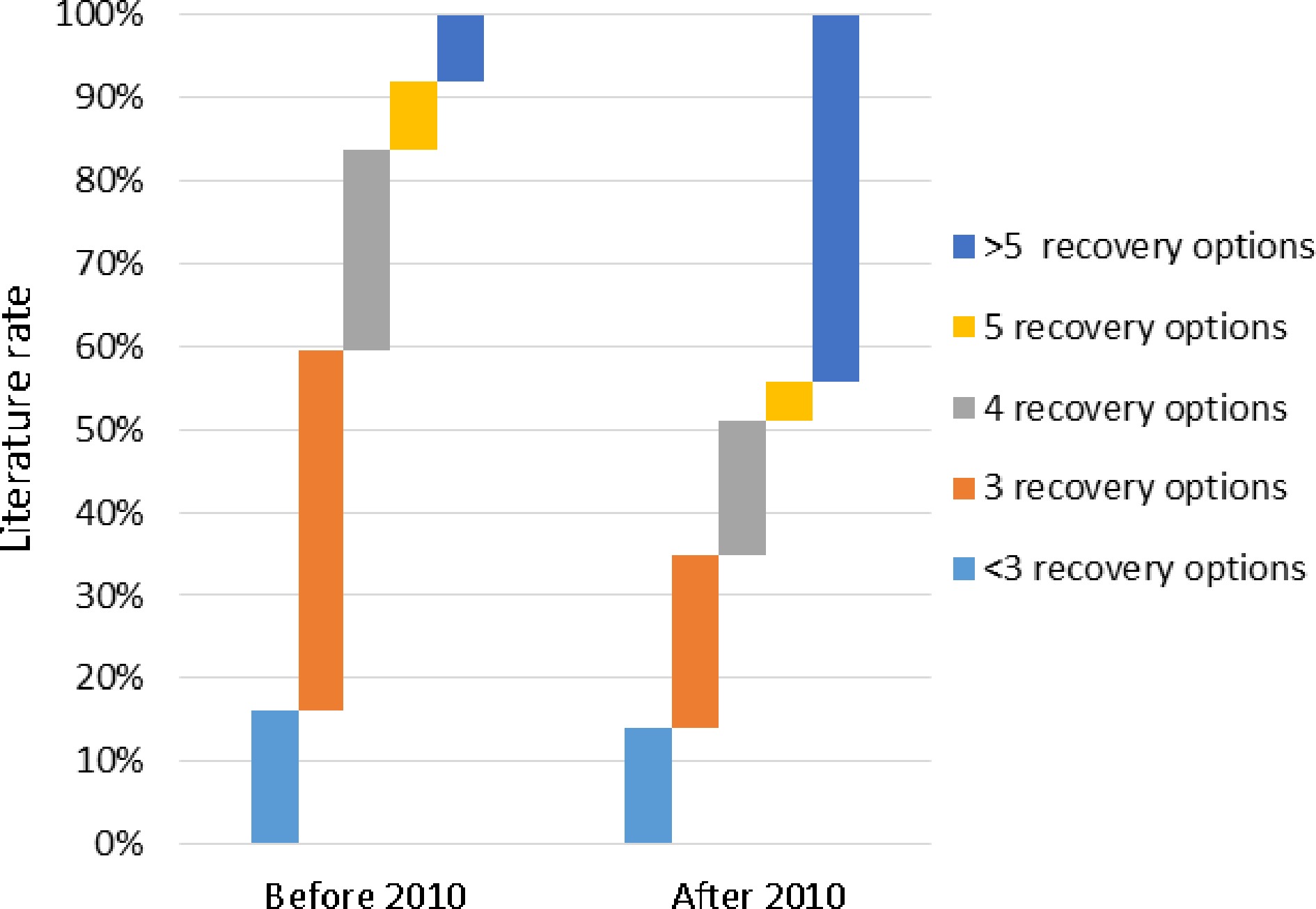
Faced with more complicated disruptions, more recovery measures should be taken to promote the recovery of original schedules. Recovery options generally vary for different resources. The recovery options for flights mainly include flight swaps, flight delays, and flight cancellations. The recovery options for aircraft are composed of fleet substitution, cruise speed control, using surplus aircraft, and ferrying. The recovery options for crews mainly include crew swaps, reserve crews, and crew deadheading. Finally, the recovery options for passengers refer to passenger itinerary rerouting, and ticket refunding. Figure 6 shows a simple statistical comparison given the number of recovery options. The vertical axis represents the literature rates of various numbers of recovery options. From Fig. 6, we know that the rate of papers considering not over five recovery options decreased from more than 90% before 2010 to approximately 55% after 2010. This indicates that more recovery options must be taken into account in recent studies.
From Figs 5 & 6, it was found that there is no direct correspondence between the number of disruption types and the number of recovery options, but there is an obvious relationship between some disruption types and the number of recovery options. For example, although airport disruption is a single type of disruption, airlines should take more recovery measures faced with such severe disruption. Additionally, from Figs 3 & 6, we also found that the number of recovery options is closely related to the recovery resources. It is noted that the literature rate of 'integrated recovery' is almost the same as the rate of '> 5 recovery options', i.e., integrated recovery of several resources can only be realized by more recovery measures.
Summary of the statistical analysis
-
A summary of the present findings based on the statistics is as follows:
(1) Twenty-eight journals published at least one paper on airline disruption management problems after 2010, which is more than before 2010, with 18 journals.
(2) The three journals with the highest number of published papers after 2010 are 'Computers & Operations Research', 'Transportation Science', and 'Journal of Air Transport Management'.
(3) More research fields have paid close attention to the area of airline disruption management after 2010, especially in the 'ENGINEERING' and 'COMPUTER' areas, in addition to 'OR/MS' and 'TRANSPORTATION' before 2010.
(4) Integrated recovery has attracted more attention; the literature rate increased from less than 10% before 2010 to more than 40% after 2010.
(5) There are two peaks in the number of papers per year: in 1997 and in 2017.
(6) The number of studies on integrated recovery increased year by year after 2006 and reached a peak in 2016.
(7) More studies focus on airline recovery problems under the occurrence of multiple disruption types after 2010, and more recovery measures are also considered in the existing literature along with the complexity of disruption.
-
According to the classification that was applied in "Statistics on various resources of airline operations" and "Trends in the number of studies by year and type of recovery resources", we will describe the studies published during the years 2010−2024 in detail. Aircraft recovery refers to the literature on aircraft recovery, Crew recovery presents the literature on crew recovery, and Integrated recovery describes the literature on integrated recovery. Therefore, the first two sections focus on the recovery of single resources. The last section concentrates on the integrated recovery of multiple resources.
Key information related to the airline disruption management problem proposed in the present reviewed papers is summarized in Tables 1−6, with Tables 1 & 2 for aircraft recovery, Tables 3 & 4 for crew recovery, and Tables 5 & 6 for integrated recovery. The information in Tables 1, 3 & 5 includes the following common attributes: 'multiobjective', 'model'. The attributes of 'objective', 'single', and 'multi' mean the paper develops a mathematical model with single or multiple objectives, respectively. The attributes of 'model', 'LP' means linear programming, 'IP' means integer programming, 'CP' means constraint programming, and 'MICQ' means mixed-integer conic quadratic. The information in Tables 2, 4 & 6 includes the following common attributes: 'solution methodology', 'data', 'data dimension', and 'solution time (sec)'. The attributes of 'data', 'RL' means the paper uses real-world instances to test the performance of the proposed model and solution methodology. The attribute of 'data dimension', aims to display the largest instance scale in the computation experiments.
Table 1. The first part of the proposed method overview for aircraft recovery.
Network Cancel Delay Aircraft swap Cruise speed Fleet Objective Model Objectives Chen et al.[29] NA NO YES YES NO Single Multi nonlinear Flight non-connection, duty swap, delay time, delay number, delay number over 30 min Liu et al.[31] NA NO YES YES NO Multi Single Nonlinear Operation, delay, passenger cost Babić et al.[32] NA YES YES YES NO Multi Single Nonlinear Max revenue minus operational and disturbance costs Liu et al.[30] NA NO YES YES NO Single Multi Nonlinear Delay time, duty swap, variance of flight delay time, number of delayed flight, number of long-delayed flight Gao et al.[36] NA NO YES NO NO Single Multi Nonlinear Weighted flight delay time Mou et al.[37] NA YES YES YES NO Multi Multi Nonlinear Delay minutes, delay, and cancellation cost Aktürk et al.[38] CN NO YES YES YES Multi Single Conic IP Delay, deadhead, additional fuel and carbon emission, passengers spilled cost Vos et al.[17] TN YES YES YES NO Single Single LP Operation, delay, cancellation, aircraft ground cost Guimarans et al.[33] NA NO YES YES NO Single Single CP Delay time Xu et al.[22] TBN YES YES YES NO Single Single IP Delay, cancellation cost Hu et al.[24] CN YES YES YES NO Multi Multi IP Min delay and cancellation cost, maximal flight delay time, min the number of swapped aircraft Wu et al.[25] CN YES YES YES NO Single Single IP Delay time Wu et al.[45] CN YES YES YES NO Multi Single IP Delay, cancellation cost Wu et al.[46] CN YES YES YES NO Multi Single IP Delay, cancellation cost Zhang[27] CN YES YES YES NO Single Single IP Cancellation, aircraft assignment, terminal balance violation cost Bouarfa et al.[40] NA NA NA NA NO NA NA NA NA Khaled et al.[41] NA YES YES YES NO Single Multi IP Operation recovery cost, number of flight changed, number of impacted airports Liang et al.[28] CN YES YES YES NO Multi Single IP Flight cancellation, route cost Lin et al.[34] NA NO YES YES NO Single Single Nonlinear Delay time Wang et al.[42] NA YES YES YES NO Multi NA NA NA Şafak et al.[39] NA YES YES YES YES Multi Single MICQ Max revenue minus fuel burn, passenger spilled, flight arrival tardiness, crew service, aircraft swap cost Vink et al.[18] TN YES YES YES NO Multi Single Mixed IP Operation and disruption cost Pei et al.[43] NA NO YES YES NO Multi NA NA NA Lee et al.[19] TN YES YES YES YES Multi Single Nonlinear Expected recovery cost Ji et al.[47] NA YES YES NO NO Multi Single Nonlinear Delay time Huang et al.[20] TN YES YES YES NO Multi Single IP Retimed, cancelled or assigned cost Şi̇mşek et al.[48] NA YES YES YES YES Multi Single Nonlinear Fuel consumption and CO2 emission cost Zang et al.[21] TN YES YES YES NO Multi Single Nonlinear Delay, cancellation cost Table 2. The second part of the proposed method overview for aircraft recovery.
Delay cost Aircraft maintenance Airport congestion Solution method Data Data dimension Solution time (s) AC Flight Chen et al.[29] NA NO NO Hybrid multi-objective genetic algorithm RL 7 70 600 Liu et al.[31] Linear NO NO Hybrid particle swarm optimization heuristic RL NA 34 236 Babić et al.[32] Linear YES NO Heuristic JAT Airways 9 47 NA Liu et al.[30] NA NO NO Hybrid multi-objective genetic algorithm RL 7 84 450 Gao et al.[36] NA NO YES Polynomial algorithm Generated 4 8 NA Mou et al.[37] Linear NO NO Polynomial algorithm Generated 5 10 NA Aktürk et al.[38] Nonlinear YES YES CPLEX An airline in the US 60 207 248.4 Vos et al.[17] Nonlinear YES NO Selection algorithm Kenya Airways 43 NA 600 Guimarans et al.[33] NA NO NO Large neighbourhood search RL 48 294 205.514 Xu et al.[22] Linear NO NO CPLEX RL 60 254 949.7 Hu et al.[24] Linear NO NO Heuristic based on ε-constraints and neighbourhood search A major Chinese airline 104 401 1200 Wu et al.[45] NA NO NO CPLEX RL 12 140 7.02 Wu et al.[25] Linear NO NO CPLEX RL 30 215 NA Wu et al.[46] Linear NO NO CPLEX RL 27 162 286.6 Zhang[27] Linear YES NO Heuristic + CPLEX RL 44 638 150 Bouarfa et al.[40] NA NA NA Multi-agent system approach NA NA NA NA Khaled et al.[41] NA YES NO ε-Constraints + CPLEX RL 11 111 30 Liang et al.[28] Linear YES YES Column generation + CPLEX RL 44 638 356.13 Lin et al.[34] NA NO NO Fast variable neighbourhood search RL 12 70 0.3 Wang et al.[42] NA YES NO Simulation RL 628 5071 NA Şafak et al.[39] nonlinear NO NO CPLEX United Airlines 81 300 8074 Vink et al.[18] Nonlinear YES NO Selection algorithm An airline in the US 100 600 44 Pei et al.[43] NA YES NO AHP + algorithm A Chinese airline 29 92 NA Lee et al.[19] Nonlinear NO YES Look-ahead approximation and sample average approximation RL NA 852 300 Ji et al.[47] NA NO NO Build-in flight feasibility verification algorithm RL NA 300 14.69 Huang et al.[20] NA NO NO Iterative copy generation algorithm Nine RL scenarios 4-162 789 0.5-855 Şi̇mşek et al.[48] NA NO Yes Aircraft Swapping and Search Algorithm Bureau of Transportation Statistics (2021) NA NA NA Zang et al.[21] Linear YES YES Decision-decomposition-based algorithm Four Chinese airlines 733 2,877 23.82 Table 3. The first part of the overview of proposed methods for crew recovery.
Network Fixed f Cancel f Delay f Crew swap Objective Objectives AhmadBeygi et al.[49] SP YES NO NO YES Single Pairing cost minus flight dual contribution Chang et al.[50] NA NO YES NO YES Multi Number of deadhead trip, unconnected flight, schedule changes and affected crews Fang et al.[51] NA YES NO NO YES Multi Deviation cost of flight time and duty time Liu et al.[52] SC NO YES NO YES Single Number of uncovered flights Luo et al.[59] SP YES NO NO YES Single Pairing cost Bayliss et al.[55] NA NO NO YES NO Single Expected crew delay Chen et al.[53] NA YES NO NO YES Multi Number of crew changes, number of duty changes, maximal duty changes, largest changed flight time, derivation of the changed duties, derivation of changed flight time Bayliss et al.[56] NA NO YES NO YES Single Cancellation Bayliss et al.[57] NA NO YES YES YES Single Delay and cancellation Wen et al.[60] DN YES NO NO NO Single Robustness-related cost Herekoğlu et al.[61] NA NO YES YES YES Multi Assignment cost, swapping cost, deadheading costs, cancellation costs, delaying costs, penalties Zhong et al.[62] NA NO YES NO YES Multi Deviation of duty time, total recovery cost Table 4. The second part of the overview of proposed methods for crew recovery.
Solution method Data Data dimension Solution time (s) Aircraft Crew Flight Recovery period (d) AhmadBeygi et al.[49] CPELX A major US hub-and-spoke carrier NA NA 329 1 2065 Chang et al.[50] Genetic algorithm An international Taiwanese airline NA 70 628 18 600 Fang et al.[51] Hybrid simulated annealing Domestic airlines NA 87 342 NA 195.04 Liu et al.[52] Simulated annealing A major airline in the US NA 482 1069 236 Luo et al.[59] Primal-dual sub-problem simplex method in a branch-and-price framework Three airlines NA NA NA 30 NA Bayliss et al.[55] Greedy heuristic Generated 37 120 300 1 1400 Chen et al.[53] Evolutionary algorithm A short-haul airline in Taiwan 270 1048 14 1080 Bayliss et al.[56] Heuristic + CPLEX Generated 37 148 243 3 3600 Bayliss et al.[57] heuristic + CPLEX Generated 74 209 566 2 600 Wen et al.[60] Customized column generation based solution algorithm An airline in Hong Kong NA NA 98 3 NA Herekoğlu et al.[61] Column generation-based
solution approachA major European airline company 400 13500 1873 3 5438 Zhong et al.[62] Ad-hoc particle swarm optimization -based optimizer Vari Flight Company NA NA 166 4 NA Table 5. The first part of the overview of proposed methods for integrated recovery.
Aircraft Crew Passenger Net-work Cancel Delay Aircraft swap Fleet Cruise speed Objective Model Objectives Eggenberg et al.[75] YES NO YES CN YES YES YES Multi NO Single IP Passengers delay, cancellation cost Jafari et al.[68] YES NO YES NA YES YES YES Multi NO Single Nonlinear Aircraft assignment, flight delay, flight cancellation, passenger disruption cost Bisaillon et al.[11] YES NO YES NA YES YES YES Multi NO Single NA Aircraft and flight operation, passenger disruption cost, constraints violation Artigues et al.[9] YES NO YES NA NA NA NA NA NA NA NA NA Mansi et al.[78] YES NO YES TBN YES YES YES Multi NO Single NA Aircraft and flight operation, passenger disruption cost, constraints violation Petersen et al.[86] YES YES YES CN YES YES YES Multi NO Single IP Flight delay and cancellation, aircraft assignment, crew pairing and deadheading, passenger delay and unassignment cost Jozefowiez et al.[76] YES NO YES NA YES YES YES Multi NO Single NA Aircraft and flight operation, passenger disruption cost, constraints violation Brunner [85] YES YES YES NA YES YES YES NA NO Single Mixed IP Flight arrival and departure delay, flight cancellation, crews' and passengers' misconnection cost Sinclair et al.[80] YES NO YES TN YES YES YES Multi NO Single NA Aircraft and flight operation, passenger disruption cost, constraints violation Hu et al.[35] YES NO YES TBN YES YES YES Multi NO Single IP Flight delay, passenger transiting, passenger refunding cost Maher[87] YES YES YES CN YES YES YES Multi NO Single IP Flight delay and cancellation, crew deadheading, and passenger reassignment cost Zhang et al.[65] YES YES NO TN YES YES YES Multi NO Single IP Flight delay and cancellation, crew misconnection, aircraft and crew swap cost Arıkan et al.[88] YES NO YES CN NO YES YES Multi YES Single Conic IP Aircraft delay, passengers delay, spill cost, swap cost, and increased fuel cost Hu et al.[81] YES NO YES CN YES YES YES Multi NO Single IP Passengers' delay, reassignment, refund cost Maher[66] YES YES NO CN YES YES YES Single NO Single IP Flight delay and cancellation, reserve crew, crew duty and deadhead cost Sinclair et al.[79] YES NO YES TN YES YES YES Multi NO Single NA Aircraft and flight operation, passenger disruption cost, constraints violation Zhang et al.[77] YES NO YES TN YES YES YES Multi NO Single NA Aircraft and flight operation, passenger disruption cost, constraints violation Arıkan et al.[88] YES YES YES CN YES YES YES Multi YES Single conic IP Flight cancellation, aircraft ferrying, crew deadheading, passenger delay, reallocation and refund, additional fuel cost, constraints violation Marla et al.[72] YES NO YES TN YES YES YES Multi YES Single IP Flight delay and cancellation, aircraft swap, passenger disruption, additional fuel cost Santos et al.[73] YES NO YES CN NO YES YES Multi NO Single Mixed IP Additional operation, passenger disruption cost McCarty et al.[64] NO NO YES CN NO YES YES NA NO Single Mixed IP Passengers' expected delay cost Yang et al.[82] YES NO YES CN YES YES YES Multi NO Multi IP Airline recovery, passenger uitility cost Yeti̇moğlu et al.[74] YES NO YES CN YES YES NO NA YES Single Nonlinear Revenue - fuel and CO2 emission cost - overnight passenger cost - spilled passenger cost. Evler et al.[89] YES YES YES NA YES YES YES Multi NO Single Mixed IP Operating and delay cost, cancel cost, connection cost, cost of assigning turnaround recovery options Xu et al.[90] YES YES YES CN YES YES YES Multi NO Single Mixed IP Cost of flight cancellation, delay, crew deadhead and unassigned passengers Zhao et al.[83] YES NO YES TN YES YES YES Single NO Single Mixed IP Disruption cost, passenger delay cost, curfew violation cost, cancel cost. Cadarso et al.[92] YES NO YES TN YES YES YES Multi YES Single Mixed IP Flight operating cost, extra fuel consumption cost, flight delay cost, passenger reaccommodation cost, passenger delay cost, crew cost, penalizes aircraft changes Ding et al.[91] YES YES YES TN YES YES YES NA YES Single Mixed IP Flight cancellation cost, passenger delay cost, external link cost, additional fuel cost and following schedule cost Chen et al.[84] YES NO YES NA YES YES YES NA NO Multi IP The total delay cost of each flight, the sum of the passenger delay time of each flight Table 6. The second part of the overview of proposed methods for integrated recovery.
Delay cost Aircraft maintenance Airport congestion Solution method Data Data dimension Solution time (s) AC Flight Crew Passenger Passenger
itineraryEggenberg et al.[75] Linear YES NO Column generation Thomas Cook Airlines 100 760 NA 30000 NA 3603 Jafari et al.[28] Linear NO NO Lingo Swedish domestic airline 13 100 NA 2236 8 NA Bisaillon et al.[11] Linear YES YES Large neighbourhood search 2009 ROADEF Challenge 618 2178 NA NA 29151 600 Artigues et al.[28] Linear NA NA NA NA NA NA NA NA NA NA Mansi et al.[78] Linear YES YES Two stage heuristic 2009 ROADEF Challenge 618 2178 NA NA 29151 600 Petersen et al.[86] Linear YES NO Bender decomposition, column generation Hub-and-spoke airline in the US NA 800 NA NA NA 2407 Jozefowiez et al.[76] Linear YES YES Three stage 2009 ROADEF Challenge 618 2178 NA NA 29151 600 Brunner[85] Nonlinear NO NO CPLEX American Airlines NA 71 26 651 651 NA Sinclair et al.[80] Linear YES YES Large neighbourhood search 2009 ROADEF Challenge 618 2178 NA NA 29151 600 Hu et al.[35] Nonlinear NO NO CPLEX A major airline in China 188 628 NA NA NA 106 Maher[87] Linear NO NO Column and row generation RL 48 262 79 28492 NA 1800 Zhang et al.[65] Linear YES NO Iteration heuristic + CPLEX Regional airline in the US 70 351 134 NA NA 72.418 Arıkan et al.[88] Linear NO NO CPLEX Airline in US NA 1429 NA NA NA 142 Hu et al.[81] Linear NO NO GRASP A major airline in China 87 340 NA NA NA 600 Maher[66] Linear NO NO Column and row generation RL 123 441 182 NA NA 1200 Sinclair et al.[79] Linear YES YES Column generation 2009 ROADEF Challenge 618 2178 NA NA 29151 1385 Zhang et al.[77] Linear YES YES Three stage 2009 ROADEF Challenge 618 2178 NA NA 29151 600 Arıkan et al.[88] Nonlinear NO NO CPLEX A major U.S. airline 402 1254 NA NA NA 1212.4 Marla et al.[72] Linear NO NO Xpress A major European airline NA 250 NA NA NA 120 Santos et al.[73] Nonlinear NO YES CPLEX Kenya airways 45 140 NA 10000 NA 3600 McCarty et al.[64] Linear NO NO Benders Decomposition + CPELX Delta Airlines NA NA NA 200 15 93.9 Yang et al.[82] Linear NO NO Genetic algorithm A major airline in China 59 209 NA 24860 NA 11 Yeti̇moğlu et al.[74] NA NO NO Novel math-heuristic algorithm A major airline in America 53 208 NA NA 2033 NA Evler et al.[89] Linear YES NO Rolling horizon algorithm Frankfurt airport 17 85 NA NA NA 45 Xu et al.[90] Linear NO NO Branch-and-cut solution method, large neighborhood search heuristic One main legacy carrier in the US NA 230 172 NA NA 937.71 Zhao et al.[83] Linear YES NO Two-stage algorithm, rolling horizon approach GE Aviation 73 207 NA 594 NA NA Cadarso et al.[92] Linear YES YES An original solution approach A IBERIA airline 19 1074 NA 1204 32 600 Ding et al.[91] Linear YES YES Variable neighborhood search algorithm Generated 50 NA NA NA NA 0.359 Chen et al.[84] Nonlinear NO NO Genetic algorithm-II A Chinese airline in Fuzhou airport NA NA NA 1818 NA 14.57 In Table 1, 'network' refers to the network type for aircraft recovery model construction: connection network (CN), time space network (TN), and time band network (TBN). The detailed network representation has been issued in Clausen et al.[8]. 'Cancel', 'delay', 'aircraft swap', 'fleet', and 'cruise speed' refer to whether the paper considers the recovery options of flight cancellation, flight delay, aircraft swapping, swapping between multiple fleet types, and cruise speed control, respectively. In Table 2, 'delay cost' means, in the proposed model, the linear or nonlinear penalty for the departure or arrival delay time of each flight. 'Aircraft maintenance' and 'airport congestion' represent whether the paper considers the constraints of aircraft maintenance and airport capacity in the proposed model.
In Table 3, 'network' represents the network applied for the crew recovery model: set partition network (SP), set covering network (SC), and duty-based network (DN). 'Fixed f', 'cancel f', and 'delay f' refers to whether the crew recovery model includes the decision variables of flight delay and flight cancellation. 'Crew swap' refers to whether the paper considers the recovery options of crew swaps. In Table 5, the first three attributes, 'aircraft', 'crew', and 'passenger', represent the combination of several resources in the recovery problems.
Aircraft recovery
-
The aircraft recovery problem (ARP) has been acknowledged as the earliest research branch compared to crew and integrated recovery in the field of airline disruption management. In addition to the smaller number and simpler rules of aircraft compared to other resources, such as crews and passengers[8], the core reason may be that aircraft are equipment, while crews and passengers are human beings. We can seek only a profit maximum or cost minimum in the ARP and can ignore the complicated psychology of human beings. This type of problem is exactly what operations research and optimization methods are good at addressing. As a classical optimization problem, there are typically two considerations in the ARP: a model formulation that accurately defines the detailed boundary of the problem and a solution methodology that shows how to obtain the solution to the problem. For this reason, categorizing aircraft recovery papers based on the model formulation and solution methodology is meaningful. Formally, these classifications are as given below. Tables 1 & 2 show the key information of the ARP literature in chronological order.
(1) Solution methodology based on network. Studies in this group are similar to most of the papers introduced in Clausen et al.[8]. The problem is formulated with networks (connection networks, time-line networks, or time-band networks) and then solved by an exact algorithm and the CPLEX solver.
(2) Meta-heuristic studies. Studies in this category seek more efficient meta-heuristics to obtain satisfactory solutions to the ARP. Note that papers in this category give less attention to model formulation. Some papers do not even include an accurate model.
(3) Polynomial studies. Studies in this category aim to analyze the optimization characteristics of the ARP in certain special situations and to design polynomial algorithms for optimal or approximately optimal solutions.
(4) Other studies. Unlike the above groups, studies in this group consider some specific approaches to analyzing the ARP.
Solution methodology based on network
-
To date, the majority of publications use integer programming solution methods to solve the aircraft recovery problem. Integer programming models are generally formulated based on various networks. Related studies by the classification of network representation will be introduced, which have been described in Clausen et al.[8] on network graphs and networks, i.e., time-space network, time-band network, and connection network.
Time-space network
-
The time-space network was first introduced by Yan & Yang[16] for flight rescheduling and aircraft recovery problems. The main advantages of the network lie in the clear graphical representation of the flight network by the time-space node and relative arcs. Moreover, the idea of discretizing flight delay time can ingeniously transform the aircraft recovery problem to a network optimization problem with boundary constraints. However, the disadvantage of the time-space network is the majority of the decision variables due to the copies of flight delay arcs. It will lead to lower efficiency in computation time. Therefore, some studies focus on the dynamic recovery methodology based on a time-space network. It can not only reduce the recovery scale but also fit the practical dynamic character of airline disruption. For example, Vos et al.[17] develop a dynamic modeling framework based on a parallel time-space network. Vink et al.[18] presented an exact mathematical model for the proposed dynamic aircraft recovery problem. Lee et al.[19] presented a stochastic reactive and proactive disruption management model that combines a stochastic queuing model of airport congestion to minimize the expected recovery costs. Huang et al.[20] proposed a copy evaluation method and develop a solution approach to the Aircraft Recovery Problem by incorporating the method within an iterative process of copy generation and filtration. Zang et al.[21] examined aircraft recovery problem from the viewpoint of balancing supply and demand across the airport time-space network through aircraft rotations between airports.
Time-band network
-
Compared to the time-space network, the time-band network plays an important role in reducing the number of flight arcs and corresponding decision variables. It divides the recovery time periods into several discrete time intervals. Of course, the core drawback of the time-band network is that the flight delay cost will be overestimated or underestimated, and even sometimes the rescheduled flight network is not feasible due to time connection failure unless the optimization result is fine-tuned. Xu & Han[22] extend the time band network for aircraft recovery in a hub-and-spoke network and use a simplex group cycle approach to control the fight disruption scope and depth.
Connection network
-
In contrast to the few studies that construct integer models based on time-space or time-band networks, more studies prefer to use connection networks, which are most popular for airline scheduling, to formulate the aircraft recovery problem. The major advantage of this network is that it is more suitable for solving large-scale problems by combining column generation and bender decomposition algorithms. One disadvantage is that it is often used for single-objective optimization in airline disruption management. Zhu et al.[23] establish a two-stage stochastic programming model based on a connection network, where the aircraft recovery time is not fixed. Hu et al.[24] describe multiobjective mathematical programming and solve the proposed problem using heuristics instead of exact algorithms. Wu et al.[25] develop a distributed computation algorithm[26] to generate feasible flight routes for solving the integer programming model based on a connection network. Zhang[27] introduces a two-stage heuristic to design an aircraft recovery network before using a set partition model. Liang et al.[28] add the constraints of aircraft planning maintenance and the airport slot capacity to the connection network and then solve it using a column generation heuristic.
Meta-heuristics
-
As an airline is more concerned with recovery time efficiency than with the optimality of the recovery solution, it is more attractive to obtain a satisfactory recovery solution in a short CPU time than to obtain a near-optimal solution over a long time for real applications in the airline industry. Therefore, heuristics have often been applied in recent years for solving aircraft recovery problems, such as the genetic algorithm in Chen et al.[29] and Liu et al.[30], hybrid particle swarm in Liu et al.[31], and neighborhood search algorithm in Babić et al.[32], Guimarans et al.[33] and Lin & Wang[34].
Polynomial algorithms
-
Although the aircraft recovery problem has been proven NP-hard[35], some studies still prefer to analyze optimization characteristics and design polynomial algorithms for some special cases of the problem. Gao et al.[36] focus on flight rescheduling under large-scale flight delays considering flight delays and flight cancellations rather than flight swaps between different aircraft routings. Then, a polynomial algorithm is designed to obtain the optimal solution for the flight rescheduling problem. Mou & Zhou[37] developed an uncertain programming model with chance constraints, where the uncertainty distribution of the aircraft delay time is given by experts. A recovery solution method is designed based on a stepwise-delay algorithm and the Hungarian algorithm. Hu et al.[24] solved the aircraft recovery problem with the hierarchical-objectives programming model by a polynomial algorithm.
Other studies on aircraft recovery
-
In addition to common concerns of aircraft recovery, some studies focus on special solution approaches to analyze or solve the proposed problem. For example, Aktürk et al.[38] and Şafak et al.[39] propose a mathematical model, especially for considering cruise speed control in the aircraft recovery problem. Bouarfa et al.[40] evaluated the performance of a multiagent system for disruption management in an airline operation control (AOC) department, and Khaled et al.[41] established a multicriteria recovery framework based on a tail assignment model. Wang et al.[42] applied a simulation method to analyze the performance of the aircraft recovery process. Pei et al.[43] presented a data-driven method to solve the flight rescheduling problem based on AHP and heuristics.
Research findings
-
(1) More studies have started to focus on multiple-fleet aircraft recovery. Approximately 15 of 25 papers (more than 50%) studied multiple fleet aircraft recovery operations after 2010, while the rate was less than 23% before 2010 according to Clausen et al.[8]. This makes the recovery model more complex due to aircraft swapping between different fleets.
(2) More studies have started to focus on multiple-objective programming to formulate the aircraft recovery problem. The model formulation in approximately six of 25 papers was developed with multiple objectives, while the number was no more than three of 31 papers before 2010. The reason is apparent. Before 2010, most solution methodologies for aircraft recovery were derived from the airline planning phase. Most model formulations were constructed for airline planning with a single objective. It can easily be solved with corresponding optimization techniques. However, due to the complexities of the real-time environment, it is difficult to use a single-objective model to accurately describe many needs of airlines. Therefore, some scholars have aimed to construct multiple-objective formulations to describe aircraft recovery problems.
(3) Almost all studies propose the common consumption that the aircraft recovery model does not consider the recovery measures of using surplus aircraft and ferrying aircraft. The assumption is realistic to some extent. Because aircraft are expensive equipment and rented instead of being bought by airlines, it is a waste of aircraft resources for airlines to leave aircraft idle or ferry spare aircraft. This is the reason why using surplus aircraft and ferrying aircraft are the last choices in actual airline recovery operations.
(4) Another common assumption in the airline recovery literature is that the flight delay cost is a linear function of delay time. This is slightly inconsistent with airline recovery practice since flight delay costs tend to be a nonlinear function of delay time[44]. Some papers, such as
Aktürk et al.[38], Vos et al.[17], Şafak et al.[39], and Vink et al.[18], attempt to make changes to solve the actual airline operation problem.(5) Airport capacity and aircraft dynamic fuel costs have begun to be considered in recovery models. This promotes disruption management more practically.
(6) More studies have started to solve aircraft recovery problems using heuristics. These heuristics include meta-heuristics and polynomial algorithms. Understandably, airline disruption management is an NP-hard problem[35], and it pursues efficient computational time rather than optimization accuracy alone in real-time. Therefore, they have to use heuristics for practical efficient application.
(7) Aircraft recovery has begun to be considered in combinatorial optimization theory. Before 2010, more studies focused on the similarity of airline disruption management and airline scheduling. However, there are clear differences between them. The airline planning stage includes the scheduling of all resources, while airline disruption management is focused on minor changes, which reduces the problem scale and provides the possibility of optimization through theoretical analysis. Moreover, aircraft recovery is the most classical optimization problem in the field of airline disruption management. Optimization analysis of airline disruption management commonly starts from the aircraft recovery problem.
Crew recovery
-
Most papers continue previous research topics such as crew recovery after the occurrence of an airline disruption. These papers include AhmadBeygi et al.[49], Chang[50], Fang & Xia[51],
Liu et al.[52], and Chen & Chou[53]. Other studies by Bayliss et al.[54−57] focus on reserve crew scheduling to reduce flight delays and cancellations under various disruption situations. Tables 3 & 4 show the key information of the crew recovery literature in chronological order.Classic crew recovery
-
AhmadBeygi et al.[49] aimed to develop a crew pairing generator to support integrated airline planning, robust planning and automated recovery in addition to modeling nonlinear constraints and cost functions in crew scheduling. Multiple solutions for crew recovery are usually obtained from the genetic algorithm used by Chang[50] and Chen & Chou[53]. Another meta-heuristic for generating multiple solutions is the hybrid simulated annealing heuristic described in Fang & Xia[51].
Reserve crew scheduling
-
Faced with airline disruptions, especially crew absence or delays, the application of reserve crews can promote the rapid recovery of airline schedules. To the best of our knowledge, airline reserve crew scheduling was first studied by Dillon & Kontogiorgis[58]. In recent decades, reserve crew scheduling for airline recovery has mainly been studied in Bayliss et al.[54−57]. Bayliss et al.[54] focus on assigning the duty start time of reserve crews in case of the disruption of crew absence. Bayliss et al.[55] extend the model for crew delay recovery. Bayliss et al.[56] focus on reserve crew scheduling for both crew absence and delay. Bayliss et al.[57] extend the influence of reserve crew scheduling on the probability of fight cancellation. Luo et al.[59] introduce a development and improvement of the proposed models and solution approaches of Sabre for crew augmentation, initially for airline safety reasons during the crew pairing process. Wen et al.[60] proposed a customized column generation based solution algorithm and on this basis, Herekoğlu & Kabak[61] utilized a customized deep learning model to provide recovery actions as inputs. Zhong et al.[62] designed an ad-hoc particle swarm optimization-based optimizer to solve Integrated Aircraft and Crew Recovery with Multi-objective and Priority efficiently.
Research findings
-
(1) In the field of airline disruption management, the crew is the other type of resource parallel to the aircraft. Crew recovery is also important for airline disruption management. Crew recovery research includes 13 papers published 14 years before 2010 and 12 papers published in the last 14 years. However, there have been research achievements in terms of problem extension and solution methodology.
(2) Although the scheduling of spare aircraft is uncommon due to the higher cost of calling a spare aircraft, studies of crew augmentation have begun to appear. After all, it is not as expensive to hire a spare crew as to hire an aircraft.
(3) In the existing literature for crew recovery, one common assumption is that the flight schedules have been recovered before the crew recovery process. Therefore, flights are generally fixed during the crew recovery process. The assumption is consistent with reality. Once the flight has been rescheduled in actual operation, only a few flights can be cancelled or delayed along with crew rescheduling. These assumptions are also considered by some papers.
(4) Although the number of papers focusing on crew recovery has not increased, more studies try to apply crew recovery problems with heuristics such as simulated annealing and genetic algorithms. There is only one paper[63] that uses a combination method of column generation and a genetic algorithm according to Clausen et al.[8], while there are no fewer than five such papers (nearly 50%) after 2010 according to our statistics.
Integrated recovery
-
Due to the complexity of airline disruption management in real situations, it is necessary to focus on the integrated recovery of multiple resources, which generally include aircraft, crew, and passengers. The integrated recovery models that are most constructed based on connection networks, aircraft routing and crew pairing are given in Clausen et al.[8]. As another important recovery resource, passenger itinerary recovery is generally formulated as follows. Let F be the set of scheduled flights and I be the set of scheduled passenger itineraries. For each flight f∈F, the number of scheduled passengers NPassf in flight f and the set of aircraft routes R(f) covering flight f are given. For each passenger itinerary i∈I, the ticket refunding cost refundci and the number of scheduled passengers NumPi in itinerary i are given. We define the integer variable ri as the number of passengers who refund their tickets and the binary variable zi as 1 if itinerary i is disrupted and 0 otherwise. R(f) denotes the set of aircraft routes covering flight i. For each r∈R(f), Capr denotes the capacity of aircraft covering routing r, and the flight delay cost of flight f in route r is denoted by delaycfr. We define the variable xr, which is equal to 1 if aircraft route r is implemented and 0 otherwise. The objective (see Eqn (1)) aims to minimize the passenger delay and ticket refunding cost. The constraints promise that passengers can refund tickets only if their itineraries are disrupted (see Eqn (2)), and the reassignment for passengers cannot exceed the seat capacities of the aircraft (see Eqn (3)).
$ \min\sum\limits_{f\in F}^{ }\sum\limits_{r\in R(f)}^{ }N Pass_f\cdot delayc_{fr}\cdot x_r+\sum\limits_{i\in I}^{ }re fundc_i\cdot r_i $ (1) $ {\rm{S.t.}}\; {r_i} \leqslant Num{P_i} \cdot {z_i}\begin{array}{*{20}{c}} {}&{} \end{array}\forall i \in I $ (2) $ \sum\limits_{i \in I(f)} {{r_i}} \geqslant N Pas{s_f} - \sum\limits_{r \in R(f)} {Ca{p_r} \cdot {x_r}} \begin{array}{*{20}{c}} {}&{} \end{array}\forall f \in F $ (3) $ {x_r} \in \{ 0,1\} \begin{array}{*{20}{c}} {}&{} \end{array}\forall r \in R(f),f \in F $ (4) $ {z_i} \in \{ 0,1\} \begin{array}{*{20}{c}} {}&{} \end{array}\forall i \in I $ (5) $ {r_i} \in \{ 0,1,...,N um{P_i}\} \begin{array}{*{20}{c}} {}&{} \end{array}\forall i \in I $ (6) The model is commonly part of the integrated recovery model, instead of being applied alone for airline recovery. Additionally, there will be slight differences in various articles for recovery variants. For example, multifleet aircraft with different seat capacities and the cost of passengers transiting between different itineraries will be considered in some studies. It is noted that passenger itinerary recovery is seldom considered separately and is often one component of integrated recovery. Only McCarty & Cohn[64] focus on the problem of performing passenger reallocation before itinerary misconnections occur. This is a proactive approach for passenger rerouting when facing uncertain itinerary delays rather than for post-disruption recovery.
According to the integration degree of the resources during the recovery process, integrated recovery publications can be analyzed in the following three categories: the integrated recovery of aircraft and crews, the integrated recovery of aircraft and passengers, and the integrated recovery of all three resources. Tables 5 & 6 show the key information of the integrated recovery literature in chronological order.
Integrated recovery of aircraft and crew
-
Zhang & Lau[65] is one of the few studies that focus on the integrated recovery of aircraft and crew. The authors first generate routes of aircraft and crews based on a time-space network and then propose a novel two-stage heuristic to solve the integrated recovery problem. Maher[66] represents a column-and-row generation algorithm framework to solve the integrated recovery of aircraft and crew problems based on Muter et al.[67].
Integrated recovery of aircraft and passengers
-
The majority of publications formulate the integrated recovery of aircraft and passengers following the multicommodity network flow model. However, there are various solution methodologies for the problem, such as directly using commercial optimizers, applying large-scale optimization methods, and designing meta-heuristics. We classify the publications according to the solution methods used in these papers.
Direct method using a commercial optimizer
-
Jafari & Zegordi[68] was the first attempt to establish a single objective model to represent and solve the integrated recovery of aircraft and passengers simultaneously based on aircraft rotations and passenger itineraries as an extension of the aircraft recovery formulation in Abdelghany et al.[69]. Based on the time-band network in Bard et al.[70], Hu et al.[35] designed a reduced time-band network to study the integrated recovery of aircraft and passengers with itineraries along a single flight. Both Arıkan et al.[71] and Marla et al.[72] add the action of speed change in addition to common recovery actions in the integrated recovery of aircraft and passengers. Another study on the passenger recovery problem under airline delay management was reported by Santos et al.[73] in daily flight operation at a hub airport under capacity limitations of the runway, taxiway and bay. Yeti̇moğlu & Aktürk[74] worked on integrated networks at which aircraft routings and passenger itineraries are superimposed, and calculated the actual profit and cancellation cost by evaluating each passenger itinerary while considering the seat capacity limitations.
Large-scale optimization method
-
Due to the large number of decision variables and constraints in the integer programming formulation of integrated recovery problems for aircraft and passengers, most publications solve them in several stages.
Some studies obtain aircraft routings in the first stage and then a passenger reassignment solution in the second stage. In Eggenberg et al.[75], the first stage focuses on the aircraft recovery problem with maintenance scheduling using column generation, and the second stage concentrates on the passenger recovery problem by computing a minimum cost flow problem with a seat capacity alternatively. Jozefowiez et al.[76] and Zhang et al.[77] both introduce a three-stage solution method for the integrated recovery problem of aircraft and passengers. In Jozefowiez et al.[76], the first two stages focus on aircraft recovery and passenger recovery successively, and the third stage attempts to transport more passengers to their destinations by creating and inserting new flight sequences into available aircraft routings. In Zhang et al.[77], however, the three stages mainly deal with aircraft recovery, flight rescheduling, and passenger recovery successively.
Other studies solve such problems by following a heuristics process; i.e., an initial solution is obtained in the first stage, and an improved optimal solution is derived in the second stage. In the first stage of Mansi et al.[78], an initial feasible solution is first obtained using mixed-integer programming models and a repairing heuristic. In the second stage, an algorithm is developed based on an oscillation strategy of alternating between constructive and destructive phases to improve the integrated recovery solution. In Sinclair et al.[79], the initial feasible solution is obtained in the first stage by a large neighborhood search heuristic. The second stage focuses on applying mixed-integer programming for integrated recovery based on a connection network.
Meta-heuristics
-
The large neighborhood search heuristic is commonly used for airline recovery, especially for aircraft and passenger recovery. Bisaillon et al.[11] represent the integrated recovery problem of aircraft and passengers with an oval description and then introduce the large neighborhood search heuristic to solve the problem. Sinclair et al.[80] improve the heuristic introduced in Bisaillon et al.[11] by adding some steps to the proposed three phases. Then, Sinclair et al.[79] use the solution result of the large neighborhood search (LNS) heuristic in Sinclair et al.[80] as the initial variables of the column generation algorithm.
Based on a neighborhood heuristic, Hu et al.[81] propose the greedy randomized adaptive search procedure (GRASP) heuristic by combining a semi greedy heuristic and the neighborhood search heuristic. Another optimization method based on a multiobjective genetic algorithm was created by Yang & Hu[82] for a novel integrated recovery problem considering passenger preferences. Zhao et al.[83] produced a two-stage algorithm compared with a rolling horizon approach. Chen et al.[84] developed an adaptive non-dominated sorting genetic algorithm-II based on dominant strengths (ANSGA2-DS).
Integrated recovery of all three resources
-
Due to the complexity of practical irregular operations in the airline industry, there are fewer studies on the fully integrated recovery of aircraft, crews, and passengers. Most papers solve the integrated problem using various methods to limit recovery scopes. For example, Brunner[85] limits recovery in a terminal airport when a ground delay program (GDP) is issued.
Petersen et al.[86] and Maher[87] solve the integrated recovery problem in several stages by column and row generation methods. Arıkan et al.[88] represent a novel flight network to limit the size of the recovery, which has been commonly used in
Aktürk et al.[38] and Arıkan et al.[71]. Few studies use heuristic algorithms like the rolling horizon algorithm[89], large neighborhood search algorithm[90], and variable neighborhood searches[91].Research findings
-
(1) Competition has greatly promoted the development of the research field. According to statistical analysis, it was found that most papers (approximately 20 publications of a total of 30 papers) focus on the integrated recovery of aircraft and passengers. The large number of studies is a benefit of the 2009 ROADEF Challenge. Approximately six papers tested their algorithms using instances from the challenge.
(2) In integrated recovery, including passenger reassignment, it is generally assumed that passengers obey the arrangement of airlines and that passengers can only stay in the original itineraries unless passengers cannot arrive at their destinations through the original itineraries. This is somewhat inconsistent with the actual recovery operation for passengers. If their original itineraries are delayed in reality, the passengers have the right to choose their itineraries: endorsing other itineraries or refunding tickets. However, it is difficult to obtain data about passengers' choices under itinerary disruption. We can still make some attempts in the field of operations research. This will promote the development of behavioral operations research in practical airline operations.
(3) Most studies assume that the passenger delay cost is a linear function of delay time, which does not fit reality. Some papers, such as Brunner[85], Hu et al.[35], Arıkan et al.[88], and Santos et al.[73], think that the passenger delay cost is based on the number of passengers or passenger classes.
(4) Methods that promote passenger recovery have begun to be proposed by combining various traveling modes. Although there are only a few publications, it is a positive attempt.
(5) In terms of the solution algorithm, heuristics have been dominant. Even if the model is directly solved by an optimizer solver, heuristic algorithms are often used. The reasons are twofold. First, due to the large scale of integrated recovery, it is difficult to achieve the required timeliness by relying directly on a commercial optimizer. Second, the goal of disruption management is to pursue the recovery of resources in a short period of time.
-
Through a qualitative and quantitative analysis of the above topics, the trends of airline disruption management are summarized below. This can provide some direction for future research, especially for new scholars in the field of airline disruption management.
(1) From the perspective of problems, two extremes may occur. One is closer to reality, and the other is related to combinatorial optimization theory.
① Airline disruption management is used to solve practical problems. Some research trends for practical application may occur in the following areas as well as in aircraft recovery problems from single to multiple fleets: i) The disruption period may be unknown and undetermined. ii) Airline disruption management should not only make flight schedules return to the original plan as soon as possible but also use fewer resources, such as swapping aircraft and crews, and consider the environmental effects of aircraft fuel. iii) Airline disruption management is commonly related to multiple agents, such as airlines and passengers. Both of their interests should be considered. iv) Future research may consider more limitations during the recovery process, such as air traffic flow constraints and airport congestion. v) Some recovery measures can also be frequently considered in the near future, such as cruise speed control, combining various traveling modes, and starting the recovery process before a disruption occurs. Although the measures are only involved in a few papers, they are commonly used in airline practical operations.
② Although airline disruption management is an NP-hard problem, under assumptions based on practical operations, some simplified problems can also have good optimal properties in terms of combinatorial optimization. Of course, this is often the task of scholars in the fields of applied mathematics and computation theory. However, anything is possible, especially in the case of interdisciplinary work becoming increasingly common.
(2) The construction of the model tends to become more complex. Combined with the analysis of practical operations of airline disruption management, models can be extended in the following directions.
① As airline disruption management aims at returning to the original plan as soon as possible, it is the goal of the recovery model to be easy to solve and to obtain a solution efficiently. It is still popular to construct an effective and simple model to exactly describe the airline disruption management process. For example, a multistage model can be established according to the peak period of flight operations in hub airports.
② For a problem with an uncertain disruption period, stochastic programming must be developed. This may exceed the research scope of traditional deterministic optimization models for airline disruption.
③ Whether aiming to complete flight recovery as soon as possible using few resources or to balance multiple agents' interests, multiple objectives should be employed. Traditional models of airline disruption management are only concerned about the recovery cost. Even aircraft rerouting must be converted into costs to simplify the model. However, the current trend is to acknowledge the necessity of the diversity of the model objectives. This is closely related to the essence of airline disruption management, i.e., minimizing the negative impacts of disruption for flights, aircraft, crew, passengers, and even hub airports.
④ Airline disruption management is closely related to multiple agents. Aircraft and crews are internal resources of the airline, while passengers are the subject of the airlines' service. Therefore, airline disruption management mainly involves the interests of the airline and passengers. However, airlines are mainly concerned with short-term economic interests, while passengers pay more attention to their psychological feelings under itinerary disruptions. Therefore, studies of passengers' feelings should be added to airline disruption management solution methodologies. A multi-agent approach, which has been proven valid for managing airline disruption management by De Castro[93] and Bouarfa et al.[40], could be applied to solve the model.
⑤ Although airline disruption management is concerned with post-disruption recovery, subsequent disruptions may continue to occur. Therefore, the robust optimization of the recovery model should be given more attention. Even the combination of robust planning before the occurrence of disturbance and disruption management after the occurrence of the disturbance should also be considered in the future.
(3) Due to the increasing complexity of the problem and model of current airline disruption management, the efficiency and effectiveness of the solution approach in both computation time and recovery period are important. After all, returning to the original plan as soon as possible is the main goal of airline disruption management.
① Heuristics have to be used more often than before in solving the problem. Multiple objective models and nonlinear models are currently often used to describe airline disruption management. Perhaps some nonlinear solvers can be capable of solving nonlinear models. However, in the short term, researchers have to resort to the combination of heuristic and commercial optimization solvers for solving the practical multiple objective model. Moreover, it is still difficult but important to promote solving multiple objective models and nonlinear models efficiently by using commercial optimization solvers.
② The actual recovery rules can be combined into the airline disruption management solution approach in future research. This will improve the efficiency. For example, changes to the flight peak period in hub airports and cruise speed have been added to the solution methodology design.
③ Machine learning can also be used for airline disruption management in several ways. First, as airline disruption management is commonly solved based on networks and in several stages, the traditional solution approach can be replaced with machine learning, in particular, deep learning based on neural networks and reinforcement learning based on a multistage recovery process. Second, new solution approaches can be generated by combining traditional combinatorial optimization algorithms and machine learning algorithms. For example, in integrated recovery, passengers' behavior and feelings can be analyzed by machine learning and data analysis methods, and then the analysis results can be used in the subsequent recovery process. Additionally, a database of historical disruption scenarios and corresponding recovery solutions can be constructed for current efficient disruption management, where the management of historical scenarios and response to current disruption requires machine learning technology. In the future, we may see some corresponding research achievements.
-
In this paper, airline disruption management papers from 2010 to the end of July 2024 were reviewed, following Clausen et al.[8]. The surveyed papers were categorized in several different ways to show the journal distribution in the area, the statistics of different resources of airline recovery, the trends in the number of papers by year and type of resources, and the statistics of disruption scenarios and recovery options, as well as providing a summary of the above statistics. The papers were further categorized based on the types of recovery resources, and for each of these categories, the structure of optimization models, the solution approach and the performance suggested by these papers were provided. This was done by defining their network, types of resources, objectives, solution methodology, case data, and running time (see Tables 1−6). In addition, the research findings for each of these categories were assessed based on a comparison with Clausen et al.[8]. Finally, the trends in the three areas of problems, models, and solution approaches were highlighted and discussed to provide researchers in the area of airline disruption management with potential future research directions. We believe that following these suggested future research directions will lead to models that are realistic and applicable for use in future airline operations.
This research was partially supported by the National Natural Science Foundation of China (71801061), the Philosophy and Social Science Research Planning Project of Heilongjiang Province (23GLB032), the Natural Science Foundation of Heilongjiang Province (LH2021G003), the Fundamental Research Special Funds for the Central Universities-Research and Innovation Fund for Doctoral Students (BK20230904), the Stable Supporting Fund of National Key Laboratory of Underwater Acoustic Technology (JCKYS2023604SSJS021).
-
The authors confirm contribution to the paper as follows: funding acquisition: Hu Y; data collection: Hu Y, Wang S, Zhang S; supervision: Hu Y, Wang S; draft manuscript preparation: Hu Y, Wang S, Zhang S, Li Z. All authors reviewed the results and approved the final version of the manuscript.
-
The data used to support the findings in this study are available from the corresponding authors upon request.
-
The authors declare that they have no conflict of interest. Yuzhen Hu is the Editorial Board member of Digital Transportation and Safety who was blinded from reviewing or making decisions on the manuscript. The article was subject to the journal's standard procedures, with peer review handled independently of this Editorial Board member and the research groups.
- Copyright: © 2024 by the author(s). Published by Maximum Academic Press, Fayetteville, GA. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
-
About this article
Cite this article
Hu Y, Wang S, Zhang S, Li Z. 2024. Review of optimization problems, models and methods for airline disruption management from 2010 to 2024. Digital Transportation and Safety 3(4): 246−263 doi: 10.48130/dts-0024-0022
Review of optimization problems, models and methods for airline disruption management from 2010 to 2024
- Received: 15 August 2024
- Revised: 16 September 2024
- Accepted: 19 September 2024
- Published online: 27 December 2024
Abstract: This paper conducts a thorough review of airline disruption management between 2010 and 2024. Unlike previous review papers, the present paper analyses the research on airline disruption management in three ways. One is to perform a statistical analysis of these papers based on the journal distribution, number of papers by year, and types of recovery resources. The second is to categorize integrated recovery methods based on the degree of integration of the resources during the recovery process: the aircraft and crew, the aircraft and passengers, and all three resources. The last way is to study the research findings based on statistical analysis and perform future research direction identification in the areas of problems, models, and solution approaches. Further, with the increasing complexity of actual demands, integrated flight disruption recovery considering multiple factors such as aircraft, crew, and passengers has become a research hotspot in recent years. For further research, we can delve deeper into issues from both practical circumstances and theoretical extensions. At the model level, more detailed characterizations are needed, along with more efficient solution methods to accommodate increasingly complex problems.