Multiclass dynamic emergency traffic collaborative assignment with parallel two-stage optimization

In the response to disaster relief, e.g., high-rise office or residence building fire disaster, etc., some affected people drive private vehicles to escape the disaster position for the sake of vehicle property and life safety, and the disaster relief resources are also transported to the disaster position by external rescue vehicles. As an important traffic and transportation infrastructure, the road network will be shared by lots of private evacuation vehicles and public rescue vehicles around the disaster position, and there exists traffic route conflicts between these vehicles. In this situation, evacuation and rescue traffic collaborative assignment is a necessary and prerequisite work to improve the multiclass traffic network efficiency.

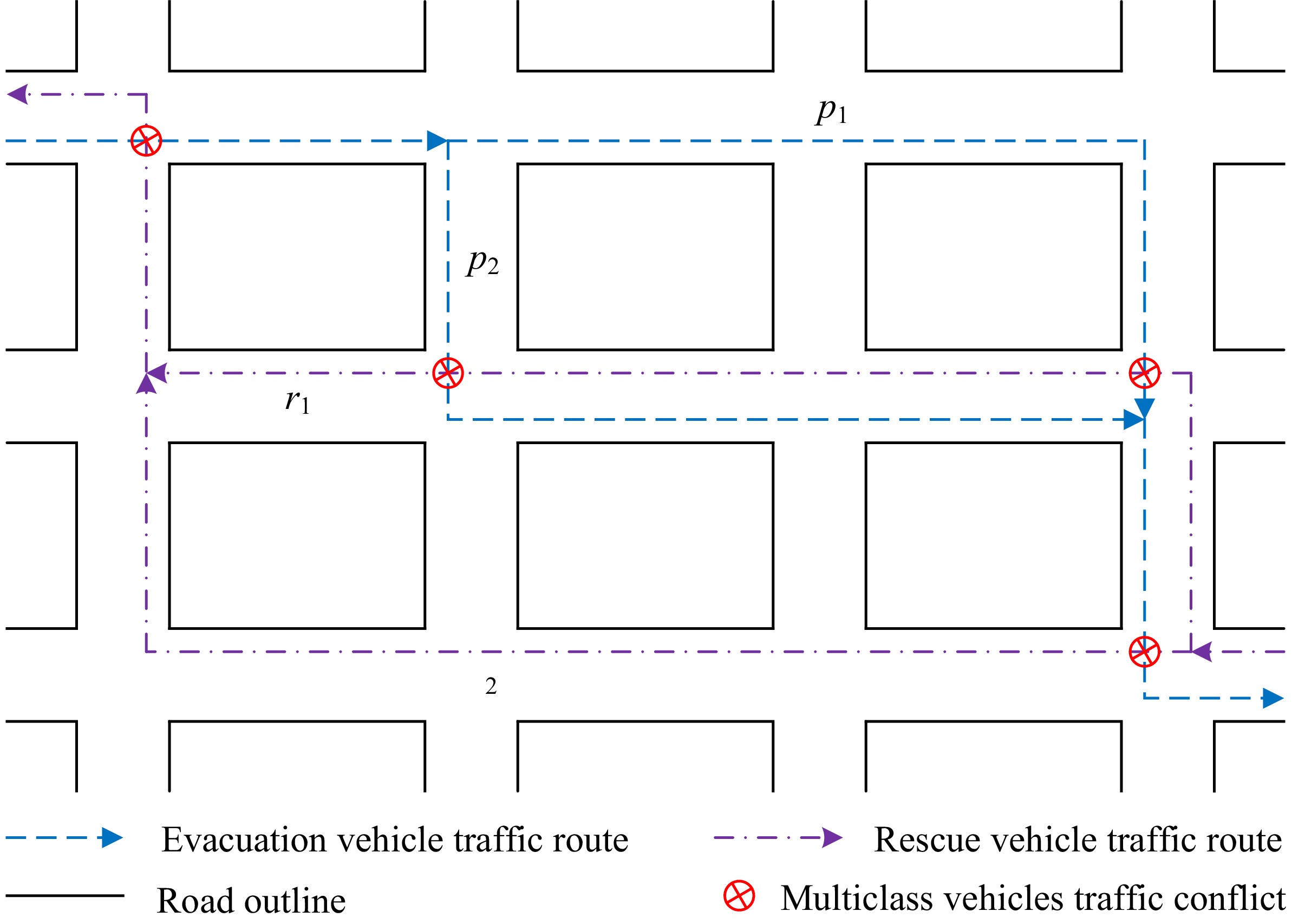
Taking a simple road network shared by evacuation vehicles and rescue vehicles as an example (see Fig. 1), evacuation and rescue traffic operation has some characteristics in practice: (1) evacuation vehicles and rescue vehicles are two different classes of vehicles, and rescue vehicles have traffic priority; (2) evacuation traffic and rescue traffic operate in the opposite direction between the disaster position and the outside street area, and they have respective dynamic operation processes and emergency response goals; (3) there exists a traffic route conflict between evacuation vehicles and rescue vehicles; (4) evacuation and rescue traffic state is dynamic, e.g., traffic speed, traffic density, traffic volume, etc., and thus, the traffic routes of evacuation vehicles and rescue vehicles are not fixed.

Figure 1. 

Feasible evacuation routes p₁, p₂, and rescue route r₁, r₂.

Based on the above-listed characteristics, there are three situations that should be considered for the improvement of the evacuation and rescue traffic operation efficiency: firstly, emergency response goals between evacuation and rescue is different, and the evacuation and rescue traffic collaborative assignment optimization problem is a multi-objective mathematical programming problem; secondly, evacuation traffic routes and rescue traffic routes are dynamic with the change of evacuation and rescue traffic states; thirdly, rescue vehicles have traffic priority in a traffic route conflict, and the route choice of rescue vehicles affect traffic evacuation. For example, as shown in Fig. 1, on the one hand, p₁ and p₂ are two feasible traffic routes for evacuation vehicles, but the travel cost on route p₂ is lower under low evacuation traffic demand. With the increase of the number of evacuation vehicles abiding on route p₂, the travel cost on route p₂ will increase and then route p₁ will be chosen by evacuation vehicles. On the other hand, r₁ and r₂ are two feasible rescue traffic routes, and rescue vehicles have the same travel cost. Considering rescue traffic priority, if rescue vehicles adopt r₁ rather than r₂ as the optimal traffic route during the evacuation, the travel cost of evacuation vehicles on p₁ and p₂ is bigger due to traffic conflicts.

Based on evacuation and rescue traffic operation characteristics, we focus on the above-listed evacuation and rescue traffic operation situations and solve multiclass dynamic emergency traffic collaborative assignment problems. Firstly, this problem is formulated as a bi-objective mathematical programming model, and its structure characteristics analyzed. Then, a parallel two-staged solving approach is designed and proven it can result in a better evacuation and rescue traffic assignment optimization solution. Based on the proposed model and solving approach, numerous evacuation and rescue traffic collaborative assignment optimization result datasets are generated under different evacuation and rescue traffic demand scenarios. Finally, some novel optimization-based data-driven conclusions are captured for evacuation and rescue traffic collaborative assignment.

Some highlights in this paper include: (1) analysis of the structure characteristics of evacuation and rescue traffic collaborative assignment optimization problems, and provide a parallel two-stage solving approach for the bi-objective mathematical programming model; (2) different evacuation and rescue traffic demand scenarios are tested, and evacuation and rescue traffic collaborative assignment optimization result datasets are generated and analyzed; (3) optimization-based data-driven conclusions for dynamic evacuation and rescue traffic collaborative assignment is captured.

The remainder of this paper is organized as follows. After the Introduction, we give a brief literature overview on evacuation and rescue traffic assignment optimization. The following section presents a bi-objective mathematical programming formulation for describing multiclass dynamic emergency traffic collaborative assignment optimization problem, and its structure characteristics is analyzed. And then, this study introduces our two-stages solving approach. On the basis of our proposed methodology, a general framework is given for evacuation and rescue traffic collaborative assignment optimization result dataset production, and we tests the proposed method with a classical road network and different disaster scenarios, and evaluates our solving approach based on the dataset analysis. At last, we outline some optimization-based data-driven conclusions for evacuation and rescue traffic collaborative assignment, and anticipate future research direction.

In a disaster emergency response, the two most important intervention activities are the transfer of the affected people and the transport of the rescue resource between the disaster position and the outside safe area, and it is necessary to optimize evacuation and rescue traffic distribution on the road network for the improvement of the traffic network operation efficiency. Here, the literature relevant to evacuation and rescue traffic assignment optimization is discussed.

In terms of evacuation traffic assignment optimization for the quick transfer of the affected people from the disaster position to the outside safe area, Zhang et al.^[1] built a mixed-integer mathematical programming model for emergency evacuation to reduce the harm of the disaster. Kimms & Maiwald^[2] studied the safe and resilient evacuation traffic assignment with the cell-transmission-based evacuation traffic optimization mathematical programming formulation. Liu et al.^[3] considered the impact of atmospheric visibility on traffic speed and road capacity, and developed a robust evacuation traffic assignment optimization model to obtain the optimal evacuation plan. To ensure the timeliness and safety of the evacuation process and reduce the loss of the nuclear accident, Xie et al.^[4] constructed a cell-transmission-based zoning evacuation traffic assignment optimization model to reduce evacuation time and exposure risk. Dai et al.^[5,6] considered the road stability coefficient and the road capacity uncertainty during evacuation, and proposed the reliability-based emergency evacuation route planning model to optimize evacuation traffic route selection and evacuation traffic flow distribution on the time-space network. Bayram & Yaman^[7] considered the joint supply and demand management, and optimized evacuation or shelter-in-place, dynamic resource allocation, and staging decisions for an efficient evacuation plan by introducing a cell-transmission-based evacuation traffic assignment optimization methodology. Du et al.^[8] focused on emergency traffic evacuation in a rainfall scenario, and developed a link-transmission-based evacuation traffic assignment optimization model to study the impact of the rainfall intensity and water depth on the evacuation traffic network operation efficiency. Liu et al.^[9] focussed on heterogeneous evacuation vehicles and road traffic congestion in the disaster emergency response, and proposed a multiclass dynamic evacuation traffic assignment optimization model to determine multiclass evacuation vehicle configuration, lane allocation, lane reversal, and intersection turn cross-elimination. Based on the existing literature, evacuation vehicle traffic assignment problem on the road network can be formulated and described by the single-objective mathematical programming model.

Multi-objective mathematical programming for evacuation traffic assignment optimization have also been studied^[10−16]. For instance, Fang et al.^[12] proposed a multi-objective evacuation traffic optimization model with the aim of minimizing the total evacuation time, the total evacuation distance, and the traffic congestion degree. Coutinho-Rodrigues et al.^[11] developed the bi-objective evacuation traffic optimization model to identify and plan evacuation paths and shelter locations. Li et al.^[17] followed several objectives and constraints, and introduced a time-extended network optimization approach for evacuation planning. Zeng et al.^[18] proposed a bi-directional multilane conflict-eliminating cell transmission model to simulate the dynamic bus and car traffic evacuation process, and then integrated it into a split delivery vehicle routing problem to formulate a mathematical programming model for dynamic evacuation with modes of bus and car. Liu et al.^[19,20] considered evacuation traffic including multiclass vehicles of different sizes, and developed the mathematical programming model for multiclass traffic collaborative evacuation and multimode evacuation traffic fleet configuration and lane allocation optimization. Liu et al.^[21] focused on managing a no-notice evacuation task for mixed traffic of private vehicles and mass-transit vehicles, and proposed a system-optimal collaborative evacuation optimization model to minimize the evacuation network clearance time. In addition to the aforementioned studies, there are further research articles regarding traffic evacuation optimization, e.g.,^[22−25]. However, multi-objective mathematical programming for evacuation traffic assignment optimization does not solve multiclass dynamic emergency traffic assignment problem consisting of evacuation vehicles and rescue vehicles.

In the response to disaster relief, there also exists rescue vehicles on the road network. Tzeng et al.^[26] proposed a multi-objective mathematical programming formulation to minimize the total relief delivery cost, minimize the total transport travel time, and ensure the fair distribution of the relief commodity among different demand points. He et al.^[27] developed an emergency rescue resource supply and road network collaborative optimization model to optimize collaborative routes of emergency resource supply and avoid rescue traffic network congestion. Guo et al.^[28] established a rescue traffic route optimization model of considering safety risk and time cost of rescue vehicles in the case where multiple rescuer groups can be dispatched from the departure point and return to replenishment point. To minimize the total risk and total cost of emergency responses, Chen et al.^[29] studied the emergency rescue route optimization problem based on a bi-objective robust optimization model. Tan et al.^[30] provided a decision tool for urban traffic accident rescue vehicles' integrated deployment problem based on a simulation optimization model. Zhan et al.^[31] focused on the urban safety early warning systems and emergency response mechanisms under snowstorm conditions.

Comparing rescue traffic with evacuation traffic, evacuation vehicles and rescue vehicles have the opposite traffic direction between the disaster position and the outside street area. Xie & Turnquist^[32] adopted the static travel time to determine the emergency traffic route from the outside street area to the affected area, and reserved the fixed emergency traffic route during the evacuation. Then, the evacuation traffic optimization problem is solved. The static shortest path does not consider the dynamic emergency traffic state and the impact of traffic evacuation. To minimize the number of evacuation vehicles abiding on the road network, Kimms et al.^[33] considered the dynamic evacuation and rescue traffic state, and developed evacuation and rescue traffic collaborative assignment optimization models. Here, the proposed formulation is solved by a hierarchical approach, in which evacuation traffic assignment and rescue traffic assignment were not optimized synchronously, and rescue traffic priority was also not obeyed. Cui et al.^[34] took the minimum of the weight of evacuation cost, rescue cost, road occupation conflict cost, and road contraflow cost as the objective, and established a minimum cost flow model to assign rescue vehicles and evacuation vehicles on the road network. However, it is difficult to ensure rescue traffic priority in road occupation conflict during the evacuation, and simulate the dynamic evacuation and rescue traffic state. Liu et al.^[35−38] developed a bi-objective evacuation and rescue traffic collaborative assignment optimization formulation to organize dynamic evacuation and rescue traffic operation process, and then the evacuation and rescue traffic route is solved respectively based on rescue traffic priority. One of the shortcomings is that the interference of rescue traffic to traffic evacuation in rescue traffic optimization is not minimized.

Taking the above-listed literature as examples, from evacuation traffic assignment optimization and rescue traffic assignment optimization to joint multiclass evacuation and rescue traffic assignment optimization, the existing methodologies neither considers evacuation traffic during the rescue nor minimize the impact of rescue traffic on evacuation traffic, and thus they are not suitable for multi-objective evacuation and rescue traffic collaborative assignment optimization problems. In such a situation, it cannot be determined whether the achieved evacuation traffic assignment result is optimal, and whether the change of evacuation result is caused by the unreasonable solving approach or the intrinsic evacuation and rescue traffic assignment coordination mechanism.

In this section, the following mathematical notations are defined to describe and model dynamic evacuation and rescue traffic operation processes on the multiclass traffic network.

A given road network is necessary to support the traffic operation of evacuation vehicles and rescue vehicles. In terms of the spatial structure of the road network, let E be the index set of all roads, and let V be the index set of all intersections; let $ E_i^ - \subseteq E $ and $ E_i^ + \subseteq E $ be the index sets of upstream adjacent roads and downstream adjacent roads that connect with road $ i \in E $; let $ \Gamma _v^{(i,j)} $ be the index set of turns that conflict with the turn from road $ i \in E $ to road $ j \in E_i^ + $ at intersection $ v \in V $. In terms of the traffic attribute of the road network, l_i represents the length of road $ i \in E $, unit: meter; Q_i is the traffic capacity on road $ i \in E $, which represents the maximum number of vehicles that can pass road $ i \in E $ within any time period $ t \in T $, unit: vehicles/$ \Delta t $; $ \rho _i^{(jam)} $ is the traffic jam density on road $ i \in E $, which represents the maximum number of vehicles that can be accommodated on road i, unit: vehicles/meter; $ {\tau _i} $ represents the traffic travel time on road $ i \in E $ in the free-flow traffic state, unit:$ \Delta t $; $ {\iota _i} $ represents the propagation time of the traffic congestion shockwave from downstream end to upstream end on road $ i \in E $, unit: $ \Delta t $.

During the whole evacuation and rescue traffic operation process, the traffic state of evacuation vehicles and rescue vehicles should be updated dynamically on the road network. Here, let $ T = \{ 1,{\text{ }}2,{\text{ }} \cdots ,{\text{ }}|T|\} $ be the index set of the time period where $ |T| $ is an upper boundary for the time needed for the completion of the whole evacuation and rescue traffic operation; $ \Delta t $ is the length of any time period; let C = {1, 2} be the index set of classes of vehicles where α = 1 represents rescue, and α = 2 represents evacuation; let D_α be the index set of emergency traffic demand where $ {d_1} \in {D_1} $ represents the number of rescue vehicles to transport the disaster relief resources from the outside street area, and $ {d_2} \in {D_2} $ represents the number of evacuation vehicles to transfer the affected people from the disaster position, unit: vehicle.

In addition, some variables are defined to decide evacuation and rescue traffic assignment plans: the nonnegative continuous variable $ y_{\alpha ,t}^{(i,j)} $ represents the number of vehicles $ \alpha \in C $ that drive into road $ j \in E_i^ + $ from road $ i \in E $ in time period $ t \in T $; the nonnegative continuous variable $ x_{\alpha ,t}^{(i)} $ defines the number of vehicle $ \alpha \in C $ abiding on road $ i \in E $ at the beginning of time period $ t \in T $; the nonnegative continuous variable $ d_{\alpha ,t}^{(i)} $ calculates the number of rescue vehicles (α = 1) that enter road $ i \in E $ from the outside street area in time period $ t \in T $, and the number of evacuation vehicles (α = 2) that enter road $ i \in E $ from the disaster position in time period $ t \in T $; the nonnegative continuous variable $ b_{\alpha ,t}^{(i)} $ calculates the number of rescue vehicles (α = 1) that enter the disaster position from road $ i \in E $ in time period $ t \in T $, and the number of evacuation vehicles (α = 2) that arrive in the outside street area from road $ i \in E $ in time period $ t \in T $; the nonnegative continuous variables $ N_{\alpha ,t}^{(i)} $ and $ V_{\alpha ,t}^{(i)} $ calculate the cumulative number of rescue vehicles (α = 1) and evacuation vehicles (α = 2) that enter and leave road $ i \in E $ by the end of time period $ t \in T $. Besides, the binary integer variable $ \beta _{\alpha ,v}^{(i,j)} $ decides whether the turn from road $ i \in E $ to its downstream adjacent road $ j \in E_i^ + $ at intersection $ v \in V $ is allowed, $ \beta _{\alpha ,v}^{(i,j)} = 1 $ is allowed, otherwise prohibited.

According to the classes of vehicles, the above-listed decision variables can be divided into two types, one type is related to rescue traffic, and are denoted as set X₁, and another type is related to evacuation traffic, and are denoted as set X₂, that is, $ {X_1} = \{ y_{1,t}^{(i,j)},{\text{ }}x_{1,t}^{(i)},{\text{ }}d_{1,t}^{(i)},{\text{ }}b_{1,t}^{(i)}, $ $ N_{1,t}^{(i)},{\text{ }}V_{1,t}^{(i)},{\text{ }}\beta _{1,v}^{(i,j)}|t \in T,{\text{ }}i \in E, {\text{ }} v \in V\} $, and $ {X_2} = \{ y_{2,t}^{(i,j)},{\text{ }}x_{2,t}^{(i)},{\text{ }}d_{2,t}^{(i)},{\text{ }}b_{2,t}^{(i)},{\text{ }}N_{2,t}^{(i)},{\text{ }}V_{2,t}^{(i)},{\text{ }}\beta _{2,v}^{(i,j)}|t \in T,i \in E, $ $ v \in V\} $. By getting the optimal solution of variable sets X₁ and X₂, evacuation and rescue traffic collaborative assignment optimization plans on the road network can be obtained.

Mathematical programming formulation

Based on the characteristics and situations of evacuation and rescue traffic network operation presented in the Introduction, a bi-objective evacuation and rescue traffic collaborative assignment optimization model is developed to plan multiclass dynamic emergency traffic operations on the road network. Based on the first situation, the emergency response goal of multiclass dynamic emergency traffic is mathematically modelled as maxf₁ and minf₂. Here, the objective function f₁ decides the number of rescue vehicles that arrive in the disaster position by the end of the current time period, where the earlier the time period for the arrival of rescue vehicles in the disaster position, the bigger the objective function f₁; the objective function f₂ consists of two parts: the first part is to evaluate the number of evacuation vehicles that still wait for the departure in the disaster position at the end of the current time period, and the second part is to evaluate the number of evacuation vehicles abiding on the road network in the current time period, and thus, min f₂ can minimize the number of evacuation vehicles that have not arrived in the outside safe area.

In the second situation, dynamic evacuation and rescue traffic operation process on the road network is simulated by Eqns (3)−(23).

Equation (3) describes the dynamic update of traffic state on the road network, and calculates the number of evacuation vehicles and rescue vehicles abiding on different roads:

Equations (4)−(7) simulate the dynamic traffic flow propagation process on roads based on the classical link transmission model^[39,40]. In Eqns (4) and (6), the decision variables $ N_{\alpha ,t - {\tau _i}}^{(i)} $ and $ V_{\alpha ,t - {\iota _i}}^{(i)} $ are defined in the non-integer time period, thus, Eqns (8) and (9) are adopted to calculate the cumulative number of vehicles that enter and leave road i by the end of non-integer time period $ t + \delta \in [t,{\text{ }}t + 1] $.

Equations (10) and (11) calculate the number of vehicles that enter and leave road i in time period t. Equations (12) and (13) ensure that all vehicles start their evacuation and rescue process, and finally arrive in their respective destinations. Equations (14)−(16) are to eliminate cross-conflict traffic turns at intersections, and M is a big number.

In Eqns (17) and (18), in the space dimension, E_R denotes set of all roads that are used by rescue vehicles, and $ {\Gamma _{\text{R}}} $ denotes set of all turns that are used by rescue vehicles, and $ \Gamma _{v,{\text{R}}}^{(i,j)} $ denotes set of evacuation traffic turns that conflict with rescue traffic turn $ (i,j) \in {\Gamma _{\text{R}}} $ at intersection v; in the time dimension, $ t_i^ \circ $ and $ t_i^ \bullet $ represent the start and end time periods that road i is occupied by rescue vehicles, and $ t_{(i,j)}^ \circ $ and $ t_{(i,j)}^ \bullet $ represent the start and end time periods that turn (i, j) is occupied by rescue vehicles. Based on rescue traffic priority, Eqns (17) and (18) represent evacuation vehicles that are prohibited from occupying these roads used by rescue vehicles until rescue vehicles pass them.

Equations (19)−(23) define the domains of the decision variables to ensure the traffic direction of vehicles is consistent with the traffic direction of the road itself. In the third situation, all decision variables should be solved synchronously to minimize the interference of rescue traffic on traffic evacuation.

Model structure characteristics

Without loss of generality, the bi-objective evacuation and rescue traffic collaborative assignment optimization model presented above can be reformulated as a general BMP (Bi-objective Mathematical Programming) structure as follows:

where, e is the identifier of constraint series, f₁(X₁, X₂) and f₂(X₁, X₂) are the first and the second objective function related with variable sets X₁ and X₂. As a function of variable set X₁, g_e(X₁) ≥ 0 denotes set of Eqns (3)−(16) and (19)−(23) to model dynamic rescue traffic operation process, and as a function of variable set X₂, q_e(X₂) ≥ 0 denotes set of Eqns (3)−(16) and (19)−(23) to model dynamic evacuation traffic operation process, and related with variable sets X₁ and X₂, h_e(X₁, X₂) ≥ 0 denotes set of Eqns (17) and (18) to eliminate traffic conflict route between evacuation traffic operation and rescue traffic operation based on rescue traffic priority.

In the BMP structure model, firstly, there is no shared dynamic traffic operation decision variables between g_e(X₁) ≥ 0 and q_e(X₂) ≥ 0, and g_e(X₁) ≥ 0 and q_e(X₂) ≥ 0 are associated by h_e(X₁, X₂) ≥ 0; secondly, h_e(X₁, X₂) ≥ 0 includes the unknow parameters. If variable set X₁ does not be solved by maxf₁ subjected to g_e(X₁) ≥ 0, the value of rescue traffic route parameters $ {E_{\text{R}}} $ and $ {\Gamma _{\text{R}}} $ is unknow, and the value of time period parameters $ \{ {(t_i^ \circ ,{\text{ }}t_i^ \bullet )|i \in {E_{\text{R}}}} \} $ and $ \{ {(t_{(i,j)}^ \circ ,{\text{ }}t_{(i,j)}^ \bullet )|(i,j) \in {\Gamma _{\text{R}}}} \} $ that rescue traffic route is occupied is also unknown. Related with variable set $ {X_2} $, variables $ N_{2,t}^{(i)} $ and $ y_{2,t}^{(i,j)} $ in h_e(X₁, X₂) ≥ 0 are also restricted by q_e(X₂) ≥ 0. Obviously, h_e(X₁, X₂) ≥ 0 is not fixed before rescue traffic route and corresponding occupation time are determined. In addition, because of rescue traffic priority, the prerequisite of solving minf₂ subjected to q_e(X₂) ≥ 0 and h_e(X₁, X₂) ≥ 0 is that both rescue traffic route denoted by $ {E_{\text{R}}} \cup {\Gamma _{\text{R}}} $ and corresponding occupation time $ \{ {(t_i^ \circ ,{\text{ }}t_i^ \bullet )|i \in {E_{\text{R}}}} \} $ and $ \{ {(t_{(i,j)}^ \circ ,{\text{ }}t_{(i,j)}^ \bullet )|(i,j) \in {\Gamma _{\text{R}}}} \} $ should have been known in advance. However, if maxf₁ subjected to g_e(X₁) ≥ 0 is solved in advance but minf₂ subjected to q_e(X₂) ≥ 0 is not solved, the impact of solving variable set X₁ on f₂ is not considered (in particular, X₁ has more than one optimal solution in the third situation presented in the Introduction).

Based on the structure characteristics of the bi-objective evacuation and rescue traffic collaborative assignment optimization model, in this section, a parallel two-stage solving approach is proposed (abbreviated as a structured BMP-PS model) to synchronously decide multiclass dynamic emergency traffic operation process, and prove it can produce the optimal solution.

Equations (24) and (25) are proposed to replace Eqns (17) and (18) and eliminate traffic route conflict between evacuation vehicles and rescue vehicles, in which Eqn. (24) restricts that evacuation vehicles and rescue vehicles do not occupy the same road i in time period t, and Eqn. (25) eliminate the conflict between evacuation traffic turn (k, l) and rescue traffic turn (i, j) at intersection v in time period t.

In Eqns (24) and (25), the binary integer variable $ \lambda _t^{(i)} $ decides that whether road i is used by rescue vehicles or evacuation vehicles in time period t, in which $ \lambda _t^{(i)} = 1 $ denotes road i can be chosen by rescue vehicles, and $ \lambda _t^{(i)} = 0 $ denotes road i can be chosen by evacuation vehicles; the binary integer variable $ \mu _t^{(i,j)} $ decides that turn from road i to its downstream adjacent road j at intersection v is used by rescue vehicles or evacuation vehicles in time period t, in which $ \mu _t^{(i,j)} = 1 $ denotes turn (i, j) can be chosen by rescue vehicles, and $ \mu _t^{(i,j)} = 0 $ denotes turn (i, j) can be chosen by evacuation vehicles.

Now, two single-objective mixed integer linear programing model P₁ and P₂ are defined as follows.

Model P₁:

maxf₁

s.t.

g_e(X₁) ≥ 0

Model P₂:

minf₂

s.t.

g_e(X₁) ≥ 0

q_e(X₂) ≥ 0

Eqs. (24) and (25)

where, $ b_{1,t}^{(i) * } $ is the optimal solution of variable $ b_{1,t}^{(i)} $ in maxf₁ subjected to g_e(X₁) ≥ 0. Noted that, since f₁ and f₂ are two objective functions based on vehicle classes and traffic priority, and they can be handled lexicographically. In the first stage, without taking variable set X₂, $ \lambda _t^{(i)} $ and $ \mu _t^{(i,j)} $ into account, Model P₁ is solved to get the optimal solution $ b_{1,t}^{(i) * } $ of variable $ b_{1,t}^{(i)} $ and the optimal value $ f_1^ * $ of the objective function f₁. In the second stage, $ \sum\nolimits_{i \in E} {b_{1,t}^{(i)*}} $ is fixed as constraints of variable $ b_{1,t}^{(i)} $, and then, Model P₂ is solved to synchronously get the optimal solutions $ X_1^* $ and $ X_2^* $ of variable sets X₁ and X₂, and the optimal value $ f_2^* $ of the objective function f₂.

Proposition:

Based on the parallel two-stage solving approach, $ \{ {X_1^*,{\text{ }}X_2^*} \} $ and $ \{ {f_1^*,{\text{ }}f_2^*} \} $ are the optimal solution and corresponding optimal objective function value in the bi-objective evacuation and rescue traffic collaborative assignment optimization model.

Proof:

In the first stage, on the one hand, because max f₁ subjected to g_e(X₁) ≥ 0 is optimized without taking the restriction of variable set X₂ and objective function f₂ into account, $ f_1^ * $ is the optimal value of rescue traffic optimization; on the other hand, the objective function f₁ is equivalent to $ (|T| - t + 1)\sum\nolimits_{i \in E} {b_{1,t}^{(i)}} $, which means that the bigger $ \sum\nolimits_{i \in E} {b_{1,t}^{(i)}} $ in the earlier time period, the bigger the objective function f₁ in the planning horizon. Therefore, $ \{ {\sum\nolimits_{i \in E} {b_{1,t}^{(i) * }|t \in T} } \} $ is the optimal and unique optimal solution of variable $ \{ {\sum\nolimits_{i \in E} {b_{1,t}^{(i)}|t \in T} } \} $ under the situation that f₁ achieves the optimal value $ f_1^ * $.

In the second stage, by minimizing f₂ subjected to g_e(X₁) ≥ 0, q_e(X₂) ≥ 0, Eqs. (24) and (25), $ \{ {\sum\nolimits_{i \in E} {b_{1,t}^{(i)} = \sum\nolimits_{i \in E} {b_{1,t}^{(i) * }} |t \in T} } \} $, the impact of variable set X₁ on both the solution of variable set X₂ and the value of the objective function f₂ is considered. Therefore, f₂ can achieve its optimal value by adjusting the solution of variable set X₁ during solving variable set X₂. Because $ \{ {\sum\nolimits_{i \in E} {b_{1,t}^{(i) * }|t \in T} } \} $ that has been obtained by solving Model P₁ does not change in Model 2, the optimal value of f₁ is still $ f_1^ * $, and $ X_1^* $ obtained by solving Model P₂ is also the optimal solution of $ f_1^ * $.

Generally, it is almost impossible to give an analytical formula to represent the optimal solution of evacuation and rescue traffic collaborative assignment problem in practice. Based on the proposed methodology, Fig. 2 gives a general framework for evacuation and rescue traffic collaborative assignment optimization result dataset production and capturing optimization-based data-driven multiclass dynamic emergency traffic collaborative assignment conclusions.

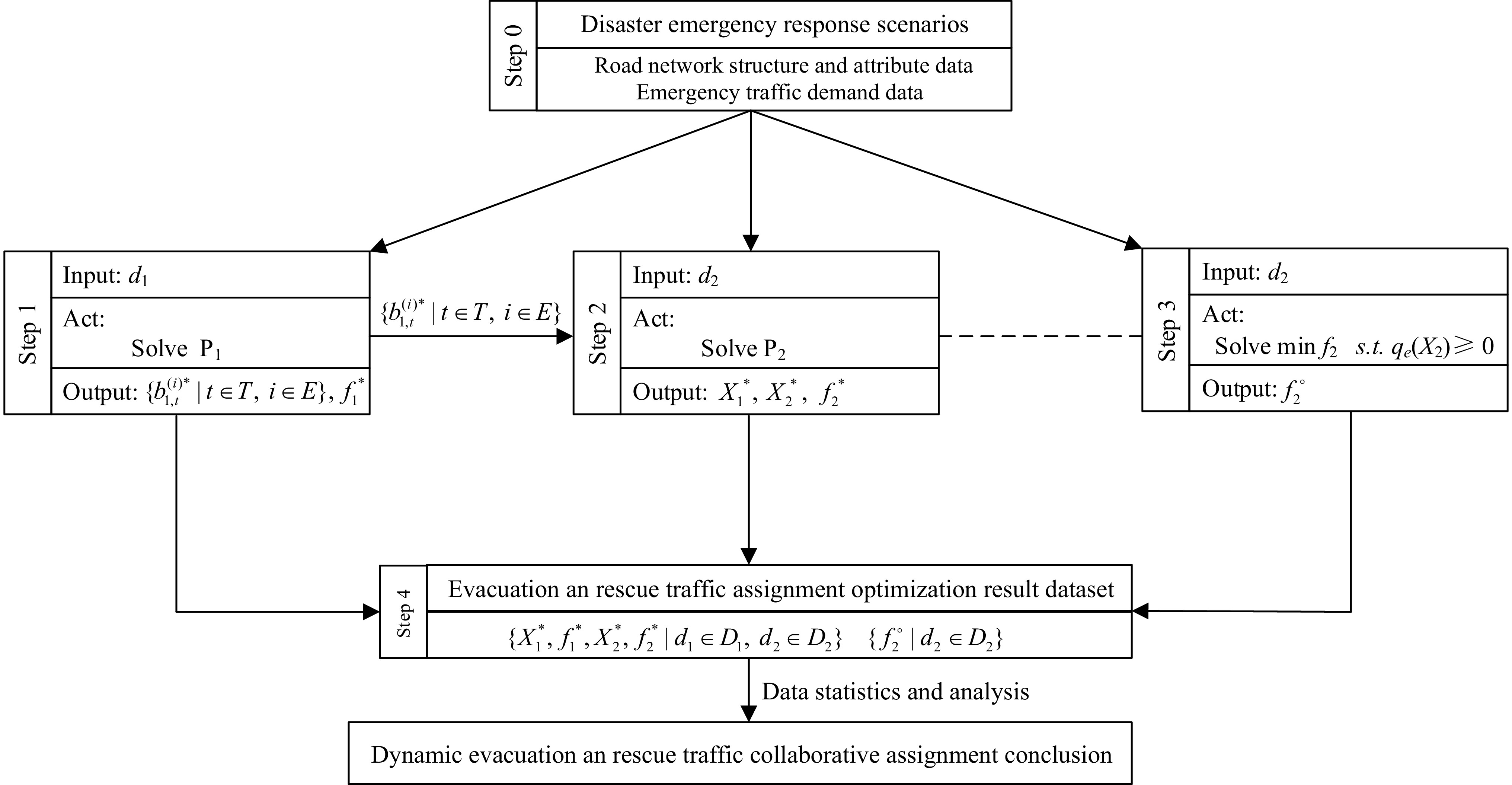
Figure 2. 

Multiclass traffic collaborative assignment optimization result dataset production framework.

Step 0 Create evacuation and rescue traffic scenarios in the response to disaster relief, and give evacuation and rescue traffic demand test sets D₁ and D₂, and develop the road network topology structure based on corresponding traffic attribute data.

Go to Step 1 and Step 3.

Step 1 Take rescue traffic demand $ {d_1} \in {D_1} $ as the known parameter and input it into Model P₁, and then, maximining f₁ subjected to g_e(X₁) ≥ 0 to get the optimal solution $ \{ {b_{1,t}^{(i) * }|t \in T,i \in E,{d_1} \in {D_1}} \} $ of variable $\{ {b_{1,t}^{(i)}|t \in T,i \in E,{d_1} \in {D_1}} \} $and the optimal value $ f_1^ * $ of the objective function f₁ in rescue traffic optimization.

Go to Step 2.

Step 2 Take evacuation traffic demand $ {d_2} \in {D_2} $ as the known parameter and input it into Model P₂, and then, minimizing f₂ subjected to g_e(X₁) ≥ 0, q_e(X₂) ≥ 0, Eqns (24) and (25), and $ \{ {\sum\nolimits_{i \in E} {b_{1,t}^{(i)}} = \sum\nolimits_{i \in E} {b_{1,t}^{(i) * }} |t \in T} \} $ to synchronously solve variable sets X₁ and X₂, and get the optimal solution $\{ {X_1^*,{\text{ }}X_2^*|{d_1} \in {D_1}, {\text{ }}{d_2} \in {D_2}} \} $ of evacuation and rescue traffic collaborative assignment and the optimal objective function value $ f_2^* $ of evacuation traffic optimization under the same evacuation and rescue traffic demand scenario with Step 1.

Go to Step 1 until all evacuation and rescue traffic demand scenarios are tested.

Go to Step 4.

Step 3 Without taking rescue traffic into account during the evacuation, take evacuation traffic demand $ {d_2} \in {D_2} $ as the known parameter and input it into minf₂ subjected to q_e(X₂) ≥ 0 to get the optimal objection function value $ f_2^ \circ $ of evacuation traffic optimization under the same evacuation and rescue traffic demand scenario with Step 1 and Step 2.

Go to Step 4.

Step 4 All possible evacuation and rescue traffic demand scenarios are tested based on Step 1−Step 3, and plenty of evacuation and rescue traffic collaborative assignment optimization result datasets consisting of $ \{ {X_1^*,{\text{ }}f_1^*,{\text{ }}X_2^*,{\text{ }}f_2^*|{d_1} \in {D_1}}, {\text{ }}{d_2} \in {D_2} \} $ and $ \{ {f_2^ \circ |{d_2} \in {D_2}}\} $ are achieved to capture optimization-based data-driven multiclass dynamic emergency traffic collaborative assignment conclusions.

In this section, the traditional hierarchical two-stage solving approach (abbreviated as BMP-HS^{[26,27,29,31,32]}) for the BMP formulation is compared with the proposed BMP-PS solving approach. In the traditional BMP-HS solving approach, rescue traffic optimization is firstly solved by maxf₁ subjected to g_e(X₁) ≥ 0, and then, evacuation traffic optimization is solved based on the fixing rescue traffic optimization result X₁ in minf₂ subjected to q_e(X₂) ≥ 0 and h_e(X₂, X₁) ≥ 0.

Testbed

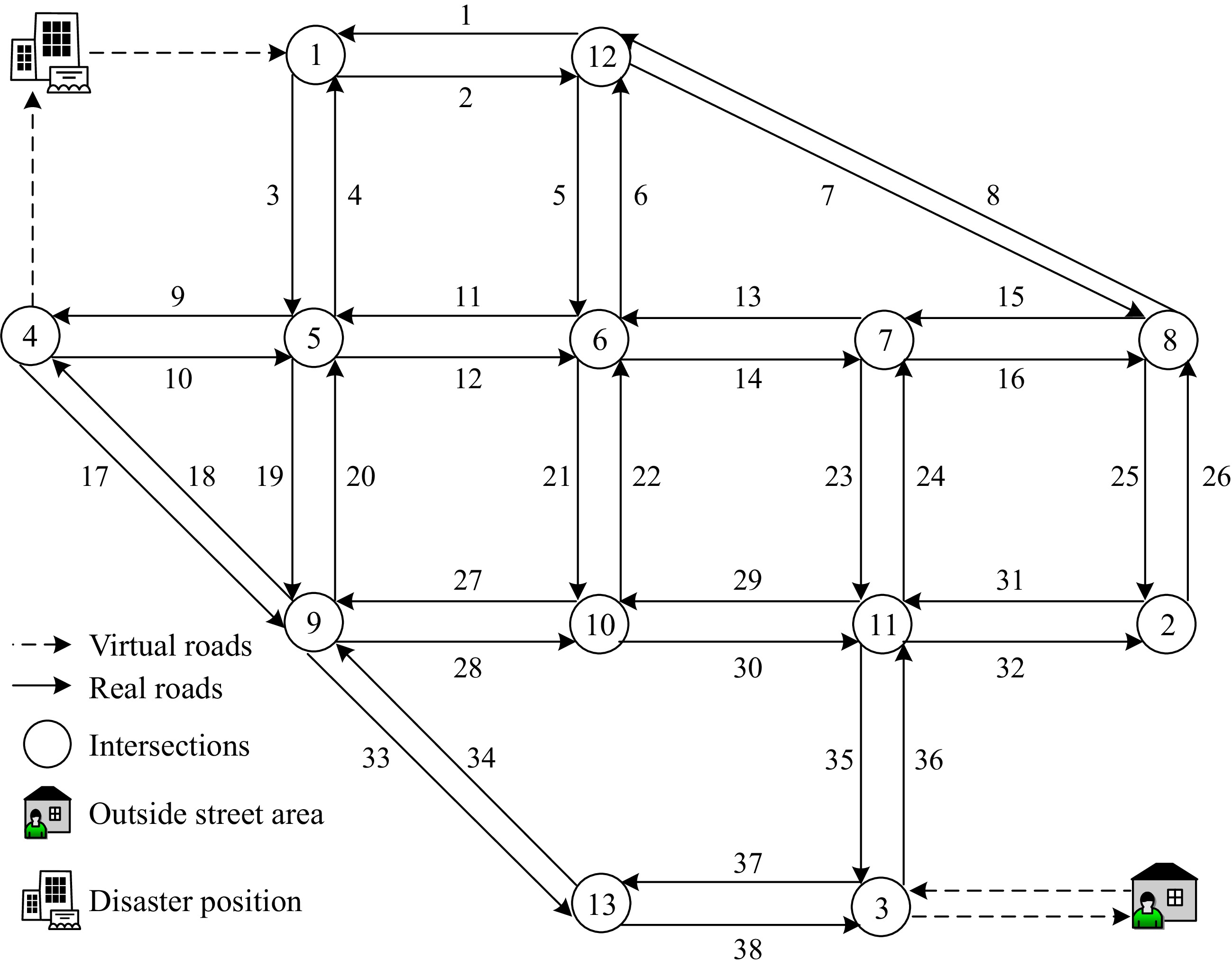
In this section, the classical Nguyen-Dupuis road network and corresponding disaster emergency response scenario are presented in Fig. 3.

Figure 3. 

Nguyen-Dupuis road network topology structure.

In terms of the road network structure and attributes, the Nguyen-Dupuis road network presented in Fig. 3 consists of 13 intersections and 38 directed roads; the length of roads 1~2, 9~16, 27~32, 37~38 is 200 m, the length of roads 3~6, 19~26, 35~36 is 400 m, the length of roads 17~18, 33~34 is 500 m, and the length of roads 7~8 is 900 m; all roads have two lanes, the traffic capacity is 2,160 vehicles/(h·lane), the traffic free-flow speed is 72 km/h, the propagation speed of the traffic congestion shockwave is 18 km/h, and the traffic jam density is 150 vehicles/(km·lane).

In terms of the disaster emergency response scenario, the disaster position is located near intersections 1 and 4, evacuation vehicles enter the road network from the disaster position and finally arrive in the outside street area via virtual roads, and rescue vehicles enter the road network from the outside street area and finally arrive in the disaster position via virtual roads. Here, all virtual roads have no traffic capacity restriction and traffic cost. In addition, the length of any time period for dynamic evacuation and rescue traffic state update is 10 s, and the time window of the whole evacuation and rescue traffic operation is 500 s; 200 different evacuation and rescue traffic demand scenarios consisting of D₁ = {30, 60, …, 300} and D₂ = {30, 60, …, 600} are tested to produce plenty of evacuation and rescue traffic collaborative assignment optimization result dataset.

Objective function values of evacuation traffic optimization

Based on the structure characteristics of the bi-objective evacuation and rescue traffic collaborative assignment optimization model, the traditional BMP-HS solving approach and the proposed BMP-PS solving approach have the same optimal arrival plans of rescue vehicles $\{ {\sum\nolimits_{i \in E} {b_{1,t}^{(i)*}|t \in T} } \} $ an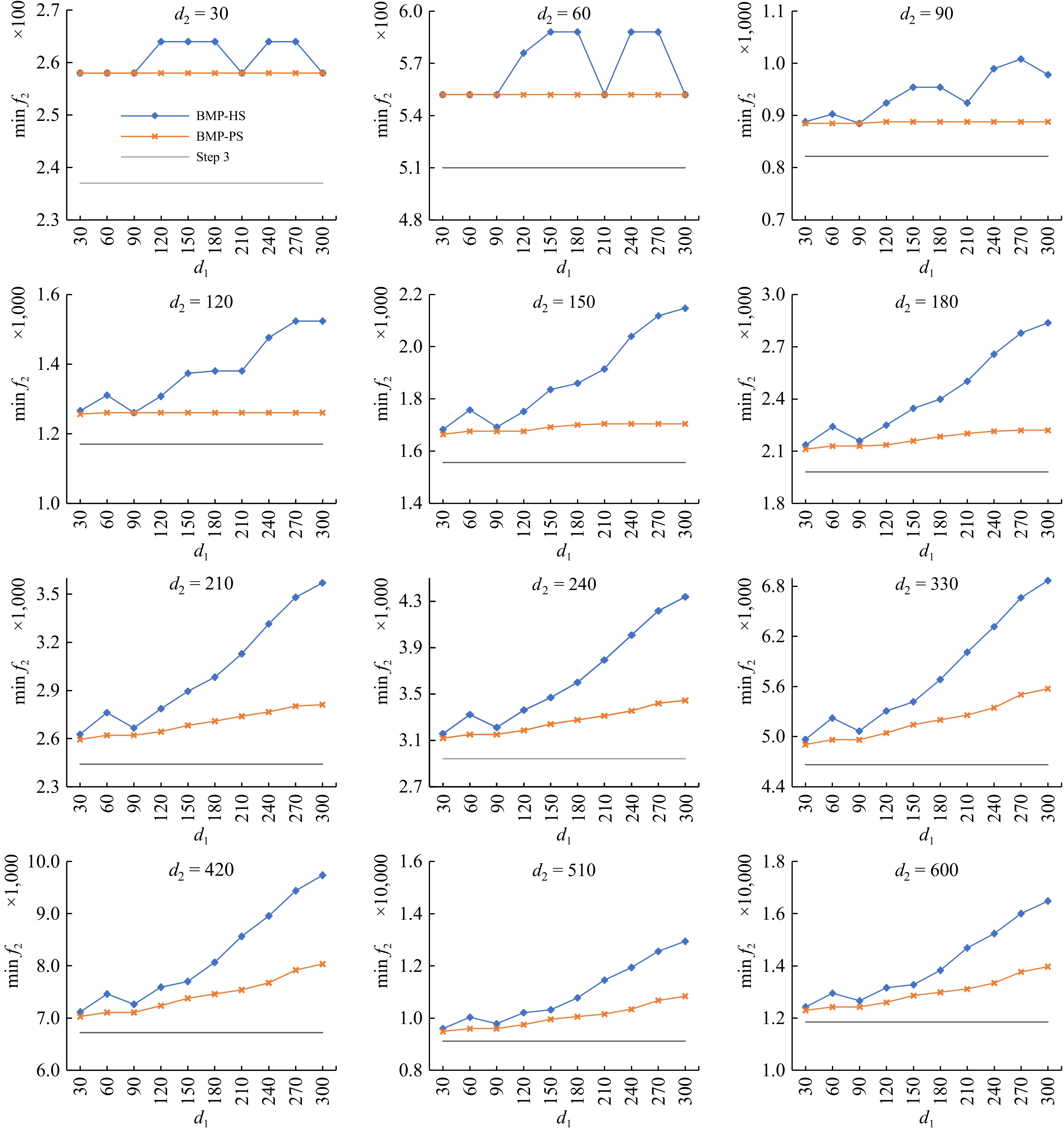d the same optimal objective function value $ f_1^* $ in rescue traffic optimization under the same rescue traffic demand d₁. Figure 4 presents the optimal objective function value dataset of evacuation traffic optimization achieved by the traditional BMP-HS solving approach, the proposed BMP-PS solving approach, and Step 3. Here, with the increase of rescue traffic demand, when evacuation traffic demand is 180, 210, …, 600, the optimal objective function value of evacuation traffic optimization has almost the same change trend, and thus, the result of evacuation traffic demands of 180, 210, 240, 330, 420, 510, 600 is presented.

Figure 4. 

Objective function values of evacuation traffic optimization in BMP-HS, BMP-PS and Step 3.

Firstly, among the traditional BMP-HS solving approach, the proposed BMP-PS solving approach and Step 3, the objective function value achieved by the traditional BMP-HS solving approach is the biggest, and the objective function value achieved by Step 3 is the smallest, and the objective function value achieved by the proposed BMP-PS solving approach is not more than the value obtained by the traditional BMP-HS solving approach. The results show when taking rescue traffic into account during the evacuation, rescue traffic operation delay evacuation traffic operations on the road network, and the proposed BMP-PS solving approach can get a better evacuation traffic optimization result than the traditional BMP-HS solving approach.

Secondly, with the increase in rescue traffic demand from 30, 60,…, to 300, the objective function value of evacuation traffic optimization achieved by the proposed BMP-PS solving approach almost remains unchanged under low evacuation traffic demand (e.g., d₂ = 30, 60, 90, 120), but these values present an obvious increase trend under high evacuation traffic demand; the objective function value of evacuation traffic optimization achieved by the traditional BMP-HS solving approach also presents an obvious increase trend under high evacuation traffic demand (e.g., d₁ = 90, 120, …, 600). Therefore, if there exists rescue traffic in high evacuation traffic demand (e.g., d₂ = 150, 180, …, 600), rescue traffic operation will have a more obvious delay to evacuation traffic under bigger rescue traffic demand.

Taking evacuation and rescue traffic demand scenarios consisting of D₁ = {30, 60, …, 300} and D₂ = {30, 60, …, 600} as examples, the proposed parallel two-stage solving approach can obtain a smaller and better objective function value of evacuation traffic optimization than the traditional hierarchical solving approach. Therefore, if rescue traffic optimization is solved without taking evacuation traffic into account and evacuation traffic optimization is solved by fixing rescue traffic, the objective function value of evacuation traffic optimization will have a more obvious underestimation (especially under bigger evacuation and rescue traffic demand), which means bi-objective evacuation and rescue traffic assignment plans underestimate evacuation efficiency and cause greater casualties and property damage in practice.

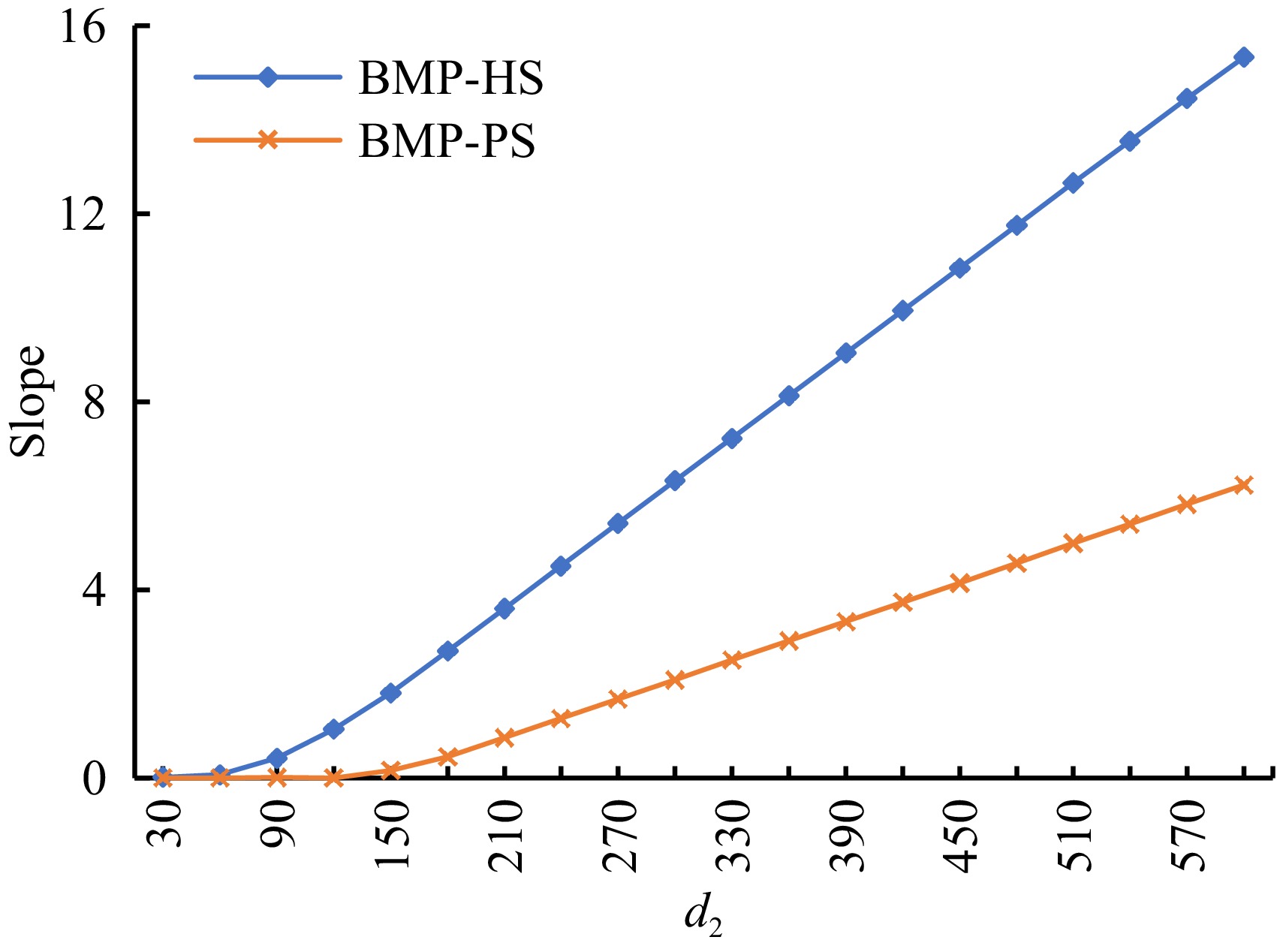
Figure 5 shows the slope of linearly fitting the curves of Fig. 4 to describe the change rate of the objective function value of evacuation traffic optimization. On the one hand, the higher the evacuation traffic demand, the bigger the slope; on the other hand, the slope obtained by the traditional BMP-HS solving approach is bigger than the value obtained by the proposed BMP-PS solving approach. Therefore, if there exists rescue traffic during the evacuation, evacuation traffic operation efficiency is more sensitive to high evacuation traffic demand with the increase in rescue traffic demand. Moreover, compared with the traditional hierarchical solving approach, a smaller slope means the proposed parallel two-stage solving approach is more resistant to interference from rescue traffic to the efficiency of traffic evacuation.

Figure 5. 

Slope of linearly fitting the optimal evacuation traffic objective function value.

Optimal evacuation and rescue traffic routes

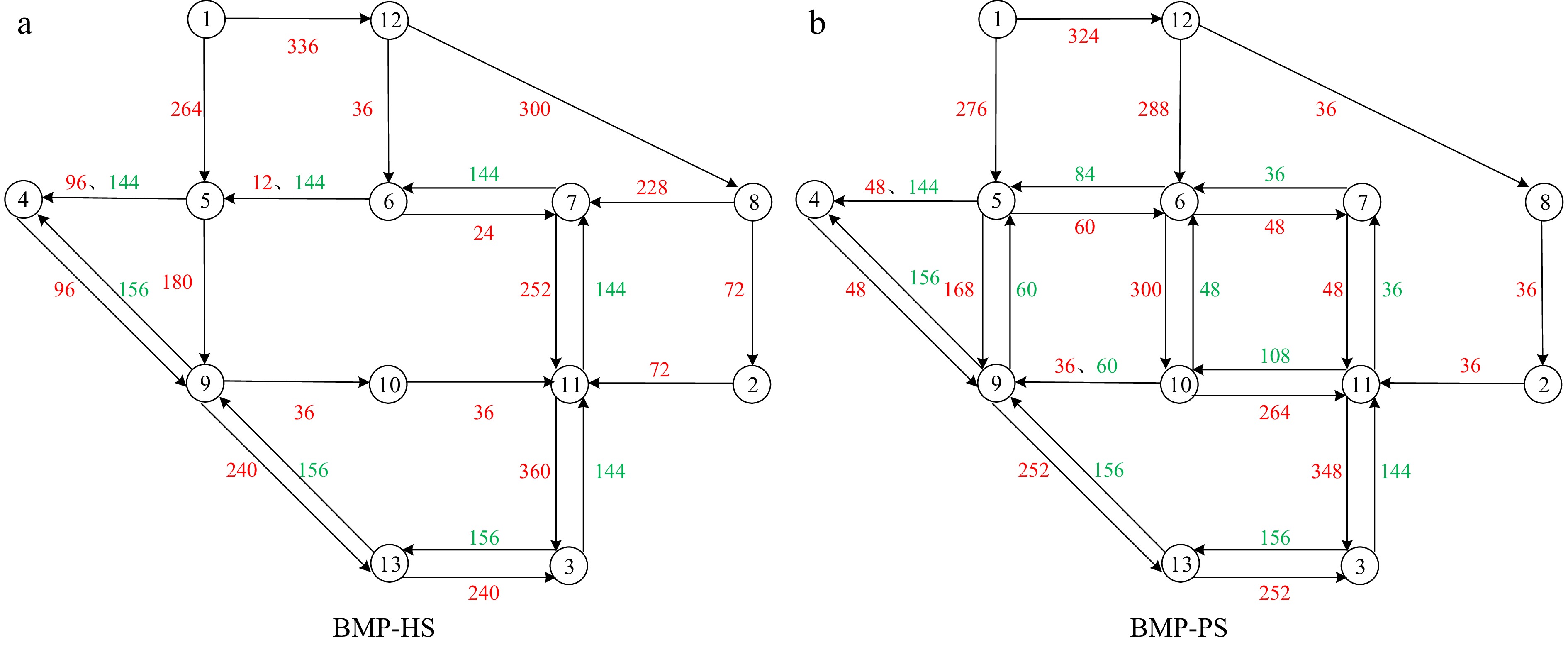
Taking rescue traffic demand d₁ equals 300 and evacuation traffic demand d₂ equals 600 as an example, Fig. 6 presents the optimal traffic routes of evacuation vehicles and rescue vehicles to realize bi-objective evacuation and rescue traffic collaborative assignment. The red and green numbers stand for the number of evacuation vehicles and rescue vehicles assigned to different roads. In Fig. 6, both the rescue traffic route and the rescue traffic volume are different between the traditional BMP-HS solving approach and the proposed BMP-PS solving approach. For example, roads 22, 27, and 29 connecting with intersection 10 are not used by rescue vehicles based on the traditional BMP-HS solving approach (see Fig. 6a), but they are used by 48, 60 and 108 rescue vehicles based on the proposed BMP-PS solving approach (see Fig. 6b). Moreover, with the change of rescue traffic routes, traffic routes of evacuation vehicles also change. The result shows, that compared with the traditional hierarchical solving approach, the proposed parallel two-stage solving approach can get different optimal rescue traffic routes and corresponding rescue traffic assignment plans that share the same optimal arrival plans of rescue vehicles in the disaster position.

Figure 6. 

Optimal evacuation and rescue traffic routes with d₁ = 300 and d₂ = 600.

Road time and space resources allocation to rescue vehicles

Figure 7 presents the number of roads occupied by rescue vehicles and the average occupation time of every occupied road in the proposed BMP-PS solving approach. 'd₂ = 0' represents there is no evacuation traffic demand during the rescue, and only rescue traffic optimization is solved by Mode P₁; 'Number of roads' is the number of roads occupied by rescue vehicles, and represents road capacity assigned to rescue vehicles during the evacuation; 'Average occupation time' represents the average number of time periods used by rescue vehicles on every occupied road.

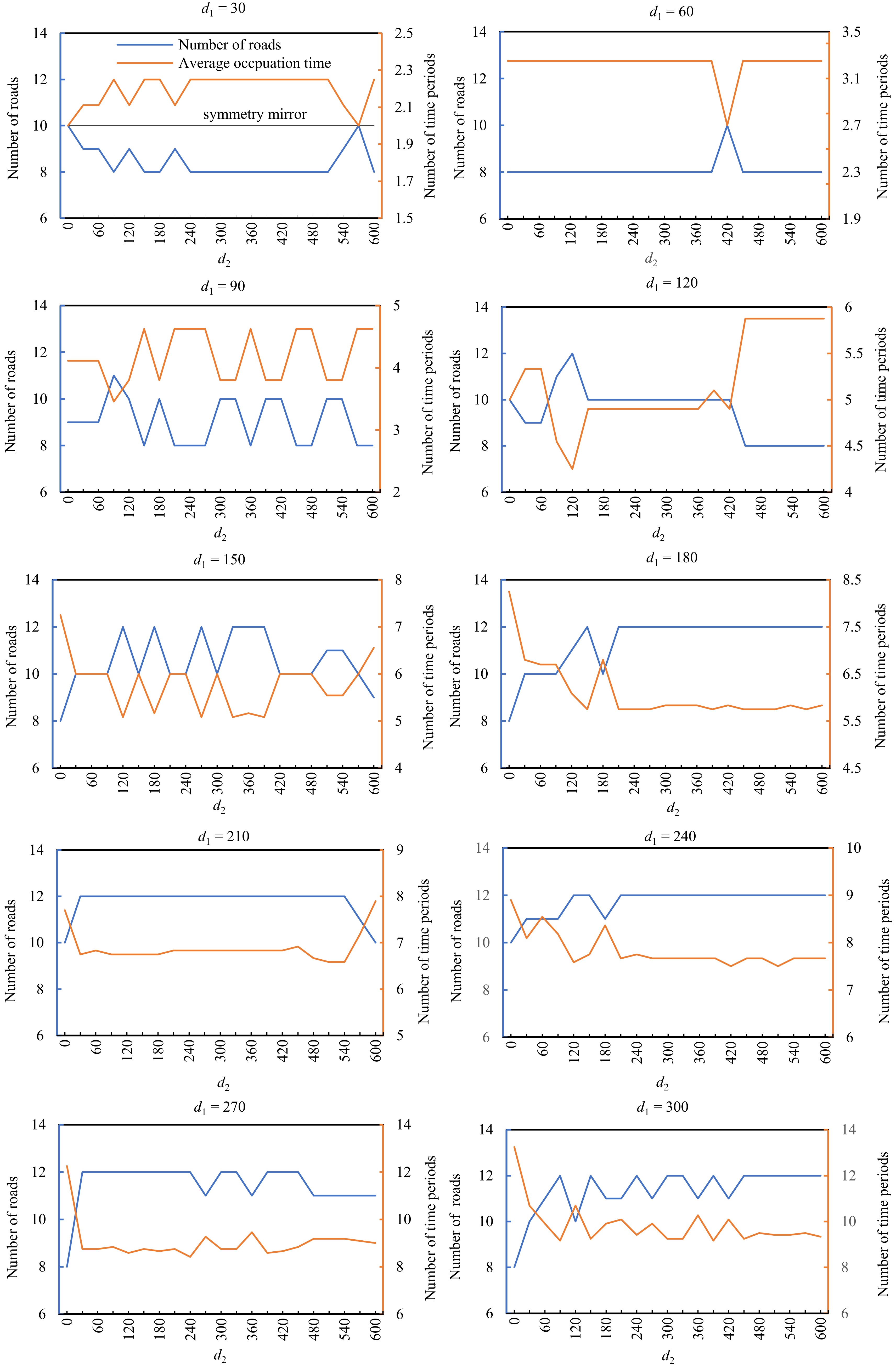
Figure 7. 

Number of roads occupied by rescue vehicles and corresponding average occupation time in BMP-PS.

As shown in Fig. 7, with the change in evacuation traffic demand during the rescue, two curves are approximate mirror symmetric under any rescue traffic demand scenario with the improvement of evacuation traffic optimization result (a better evacuation traffic optimization result in BMP-PS has been represented by Fig. 4). Here, if the number of roads occupied by rescue vehicles during the evacuation (d₂ = 30, 60,…, 600) is bigger than the number of 'd₂ = 0', the corresponding average occupation time is smaller; conversely, if the average number of the time period used by rescue vehicles on every occupied road is bigger than the average occupation time of 'd₂ = 0', the number of roads occupied by rescue vehicles is smaller during the evacuation. The mirror symmetry law of one increase, one decrease and one improvement shows adjusting time resource allocation and space resource allocation of the road network in reverse to rescue vehicles can get better evacuation traffic optimization results without delaying the arrival of rescue vehicles in the disaster position, and finally realize evacuation and rescue traffic collaborative assignment.

As shown in Fig. 7, when rescue traffic demand d₁ is 30, the number of roads occupied by rescue vehicles during the evacuation is smaller than the number of 'd₂ = 0', but the corresponding average occupation time is bigger; when rescue traffic demand d₁ is 150, 180, …, 600, the number of roads occupied by rescue vehicles during the evacuation is bigger than the number of 'd₂ = 0', but the corresponding average occupation time is smaller; compared with the value of 'd₂ = 0', rescue traffic demand of 60, 90, 120 is a transition state in terms of the change of both the number of roads occupied by rescue vehicles and corresponding average occupation time during the evacuation. The result shows decreasing the number of roads occupied by rescue vehicles and increasing average occupation time of every occupied road in low rescue traffic demand, but increasing the number of roads occupied by rescue vehicles and decreasing average occupation time of every occupied road in high rescue traffic demand can improve evacuation traffic operation efficiency without delaying the arrival of rescue vehicles in the disaster position.

This paper contributed a parallel two-stage solving approach and some optimization-based data-driven conclusions to the literature for multi-objective multiclass dynamic emergency traffic collaborative assignment problem. The parallel two-stage solving approach was evaluated and has a comparison with the traditional hierarchical two-stage solving approach in a computation study. The present approach is meaningful and achieves three main interesting facts about evacuation and rescue traffic collaborative assignment on the road network.

(1) Rescue traffic operation delays the quick arrival of evacuation traffic to the outside safe street from the disaster position. In a high evacuation traffic demand scenario, there has a more obvious delay to evacuation traffic with the increase of rescue traffic demand. However, the parallel solving approach can obtain a better evacuation traffic optimization result than the traditional hierarchical solving approach.

(2) If rescue traffic assignment is optimized without taking evacuation traffic into account and evacuation traffic optimization is solved by fixing rescue traffic routes, evacuation traffic operation efficiency from the disaster position to the outside street area has a more obvious underestimation (especially under the big evacuation and rescue traffic demand scenario).

(3) When realizing evacuation and rescue traffic collaborative assignment, there exists the mirror symmetry law to time and space resources allocation of the road network for the quick arrival of rescue vehicles in the disaster position during the evacuation. Moreover, the mirror symmetry law can improve evacuation traffic operation efficiency during the rescue.

Overall, these facts indicate that the present two-stage solving approach can reduce the interference of rescue traffic on traffic evacuation without delaying rescue traffic operation efficiency, and thus, the proposed parallel-solving approach can be used to develop a more efficient emergency traffic network organization and operation plans for the potential fire disaster of the high-rise office or residence building, and can also provide a new multiclass dynamic emergency traffic collaborative assignment approach for evacuation and rescue traffic collaborative control. Meanwhile, there also exists some shortcomings in this paper, for example, it is assumed that social vehicles are prohibited from driving on the road network around the disaster position, and neglect the impact of social traffic; the traffic attribute difference of rescue vehicles, e.g., fire vehicles, ambulance vehicles, police vehicles, and the distribution of the outside rescue stations are not considered.

In future research, it would be interesting to train a data-driven machine learning model based on the evacuation and rescue traffic collaborative assignment optimization result datasets, and compare it with the optimization-based solving approach in terms of solution efficiency and solution performance. In such a manner, more intelligent and adaptable multi-objective multiclass dynamic emergency traffic collaborative assignment methods may be proposed for more complexity disaster scenarios, e.g., traffic control, multi-origin heterogeneous emergency traffic flow, emergency traffic demand uncertainty, etc.