Review of optimization problems, models and methods for airline disruption management from 2010 to 2024

Introduction

Airline scheduling in the civil aviation industry is very complex. It usually starts a few months in advance and involves millions of flights. In the past few decades, optimization research on airline scheduling has obtained rich results^[1,2], especially in the field of operations research.

However, the daily operations of the original airline schedules are often disrupted by internal or external factors, such as severe weather, crew reassignments, and maintenance problems. These disruptions may result in great economic damage and damage to the reputations of airlines. It is impossible to completely eliminate the losses caused by these disruptions. Currently, a common recovery method is to reschedule resources, such as aircraft, crews, and passengers, to bring the flight schedules back to the original situation as quickly as possible and minimize the losses caused by the disruptions. This strategy is defined as airline disruption management^[3].

In recent years, the factors causing disruptions have become increasingly complex. As individual awareness has grown, disruptions due to strikes or staff shortages have become more frequent. The integration of smart aviation means more technological applications, but it has also brought a higher risk of large-scale flight disruptions. The frequency and scale of flight interruptions are both on the rise. Therefore, it is always a challenge to obtain efficient solutions for airline disruption management for both the civil aviation industry and operations research scholars.

Previous research and motivation

Since the study of airline schedule recovery began with Teodorović & Guberinić^[4], it has been a topic of concern for an increasing number of researchers. Etschmaier & Mathaisel^[5] introduce an overview of airline scheduling from the perspective of operations research over the previous 20 years and points out the necessity of future research on airline schedule recovery. At the end of the 20^th century and the beginning of the 21^st century, airline recovery research grew explosively. and classic models and methodologies of aircraft recovery and crew recovery were proposed by scholars such as Yan, Clarke, Bard and Yu.

The formal definition of airline disruption management was not given until Yu & Qi^[3]. They^[3] point out that airline disruption management mainly refers to the recovery of two airline resources: aircraft and crew. It also systematically constructs a network of aircraft and crew recovery. However, there are only a few reviews of the airline disruption management problem from the perspective of operations research.

Ball et al.^[6] explicitly describe three aspects of airline schedule recovery: aircraft recovery, crew recovery, and passenger recovery. Moreover, they give a classic model formulation of the recovery of each resource. Kohl et al.^[7] not only give a detailed introduction to various aspects of airline disruption management but also use actual project experience with airline disruption management. This is the first review paper that proposes including passenger itinerary recovery in airline disruption management. Clausen et al.^[8] provide a detailed overview of the network for airline schedules. This confirms that the solution methodology used for airline disruption management is similar to that used for airline schedule planning. Moreover, it introduces a thorough review of airline disruption management with the resources of aircraft, crews, passengers and integrated recovery. Artigues et al.^[9] discuss the ROADEF 2008/2009 Challenge, an international competition organized by the French Operational Research and Decision Support Society (ROADEF). This challenge presents an airline disruption management problem, i.e., recovering flight planning, aircraft assignments, crew, and passenger itineraries in a given period under one or more airline disruptions. It first introduces the detailed problem posed by this challenge, then reviews the most common solution methodologies applied in the challenge, and finally compares the solution results among nine different teams entering the final round. The review gives one important instance of airline disruption management applied to practical industry. The publication of challenge data has promoted a large number of research papers focusing on airline integrated recovery in subsequent years. Visentini et al.^[10] define the airline schedule recovery problem as a real-time vehicle schedule recovery problem (RTVSRP) and categorize related literature according to the disruption types given by Bisaillon et al.^[11]. Hassan et al.^[12] provided a review of airline disruption management between 2009 and 2018. However, no comparison is illustrated with Clausen et al.^[8]. The robustness of recovery strategies is also an important factor.

Research contributions

(1) A statistical analysis and comparison between two periods. Based on the collected papers from the period 2010-2024, a statistical analysis of the journal and field distribution, the types of recovery resources, the trend in the number of studies by year, and disruption types and recovery options are provided. Moreover, comparisons are drawn between the selected papers and the literature in Clausen et al.^[8].

(2) A classification of integrated recovery based on a combination of recovery resources. In previous review papers, the airline disruption management problem has included the aircraft recovery problem, crew recovery problem, and integrated recovery problem. The integrated recovery problem is further divided into integrated recovery of aircraft and crew, integrated recovery of aircraft and passengers, and integrated recovery of total resources.

(3) An identification of research directions. Conclusions from the current literature are drawn and then future research directions identified in three areas: problems, models, and solution methods for airline disruption management. We intend to work in some of the research directions in this field. We also hope that other scholars will work in this field so that collectively, our research can promote achievements in the theory, methodology, and technology of airline disruption management.

Organization of the paper

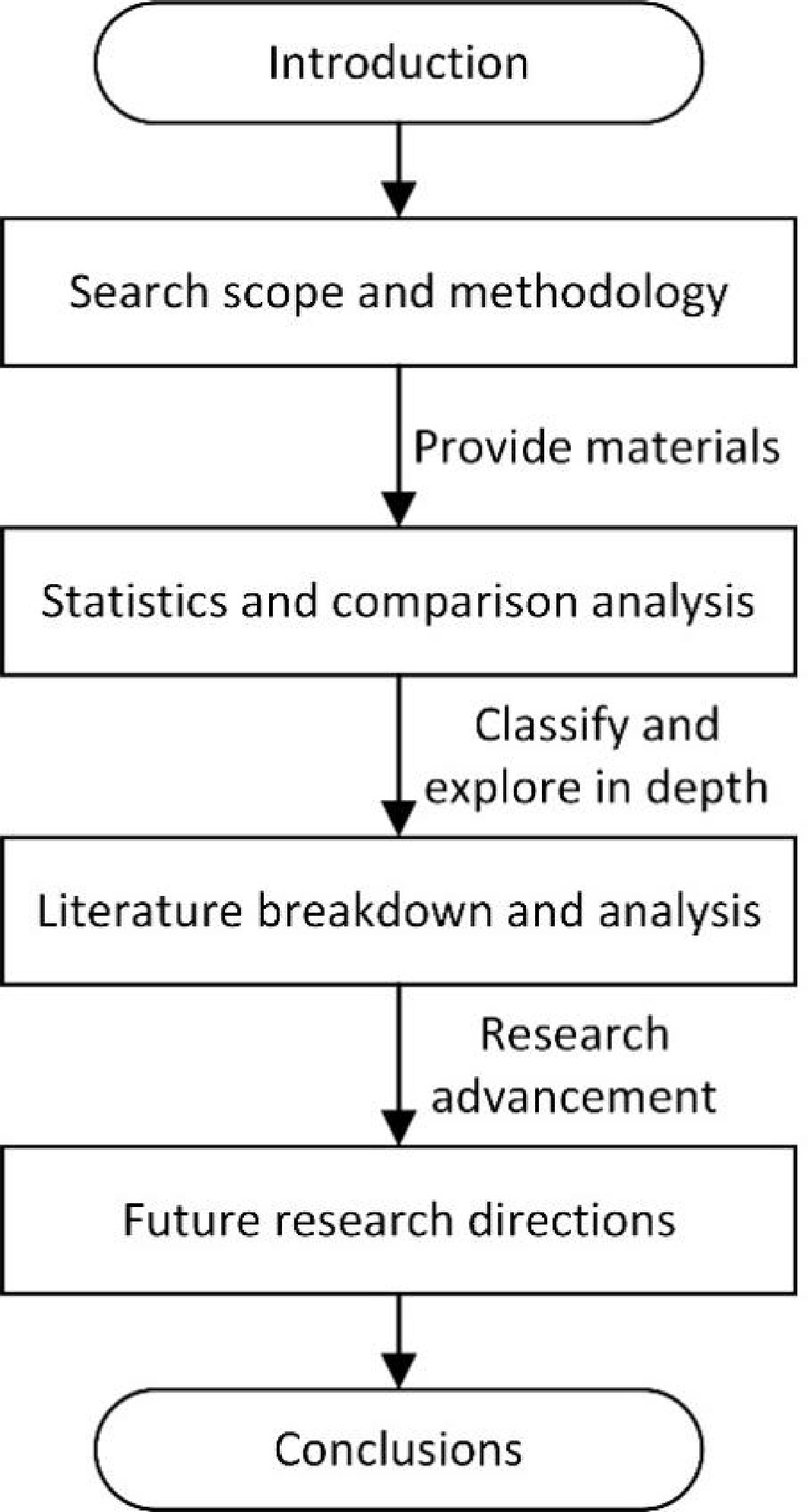
The remaining content of the paper is organized as follows: In the next section, we define of airline disruption management and the search range of the collected literature. This is followed by a statistical analysis that is compared with that of Clausen et al.^[8]. Detailed information and corresponding research findings in the literature related to aircraft, crew, and integrated recovery are presented next. Future research directions in the three areas of problems, models, and solution methods are presented in the following section. Finally, conclusions are drawn. Research contents and the relationship between each section are shown in Fig. 1.

Figure 1.  Research contents and relationship between each part of the paper.

DownLoad: Full-Size Img PowerPoint

Search scope and methodology

Definition of airline disruption management

Currently, there is no unified and clear definition of disruption management in the academic field. However, most scholars have reached a common view. According to Yu & Qi^[3], disruption management is a methodology that addresses disruptions in real-time. At the beginning of a business cycle, an optimal or near-optimal operational plan is obtained by using certain optimization models and solution schemes. When such an operational plan is executed, disruptions may occur from time to time that are caused by internal and external uncertain factors. As a result, the original operational plan may not remain optimal or even feasible. Consequently, we need to dynamically revise the original plan and obtain a new plan that reflects the constraints and objectives of the evolved environment while minimizing the negative impact of the disruption. Clausen et al.^[8] limit disruption management to the basic goal of returning to the original plan as soon as possible to minimize system disturbance.

Although disruption management is currently not applied to the airline industry alone, the definition of disruption management indeed began with airline civil aviation. According to Yu & Qi^[3], airline disruption management refers to disruption management for applications in airline operations. Airline disruption management is commonly implemented by an airline operation center (AOC). When a disruption occurs, the airline first needs to assess the disruption and then make revisions to their flight planning and the schedules of related resources.

In Yu & Qi^[3], the recovery resources primarily include the aircraft and crew. Clausen et al.^[8] report that passenger itineraries have also been included in recovery resources since Lettovsky^[13] and Bratu & Barnhart^[14]. Therefore, airline disruption management currently involves aircraft, crew, and integrated recovery of three resources, including passenger itineraries.

Aircraft recovery problem: When flight schedules are disrupted, the problem tries to minimize the division from the original schedules in terms of aircraft and flight operations. Generally, where some aircraft can be rerouted (aircraft swap), some disrupted flights can be given a new departure and arrival time (flight delay), and some disrupted flights can be cancelled (flight cancellation).

Crew recovery problem: when the flight schedules are recovered, the problem attempts to make a crew rescheduling decision to minimize the division related to crew schedules. Sometimes, flights can be delayed or cancelled as well.

Integrated recovery problem: During the recovery process, the problem aims to consider two or three recovery problems, such as aircraft recovery, crew recovery, and passenger itinerary recovery, in an integrated model.

Search methodology

After understanding the core concepts of airline disruption management, we focused on the task of finding published journal papers related to airline disruption management. To do this, a systematic approach was used, as described in what follows. The search began with the databases of ISI's Web of Science, ScienceDirect, and the Wiley Online Library. The keywords 'airline', 'aircraft', 'crew', and 'passenger' combined with 'perturbance', 'disruption', 'disrupted', 'irregular', 'recovery', 'rerouting', 'cancellation', 'delay', 'rescheduling', and 'reassignment' were searched in the titles of journal papers published in English. Book chapters and working papers were excluded. The period of the search was limited to 2008 and thereafter. To be more precise, if a journal paper related to the present topic was included in Clausen et al.^[8], it was excluded from the present study. Therefore, most of the papers were published between 2010 and 2024.

After searching for the defined keywords in the mentioned journals, 1384 papers were obtained as the initial results. We were certain that many of these papers would not fit within the project scope. Hence, we continued extracting the papers most related to the topic of airline disruption management.

The titles and abstracts of the papers were checked and papers eliminated with titles completely different from the present research domain. For example, papers with titles or abstracts related to disruption management in railway transportation, public transportation, vehicle routing problems, and aircraft manufacturing were eliminted. Some papers focusing on airline delay prediction, delay propagation, airline gate assignment, air traffic flow management, and airport terminal optimization phases were also filtered out. By applying the above filters, 69 papers were identified for the present survey.

Statistics and comparison analysis

Statistical analysis and comparison of the published literature is now provided between 2010 and 2024, and before 2010. The papers published before 2010 are derived from Clausen et al.^[8]. The characteristics of these papers are analyzed, namely, the journal and field distribution, the types of related resources, and the trend in the number of studies by year.

Journal and field distribution

The 69 selected papers were published in 29 journals and three types of conference proceedings after 2010. The statistical results from Clausen et al.^[8] are provided for comparison. There were a total of 18 journals and five types of conference proceedings before 2010. This illustrates that the articles published after 2010 involve more journals than those published before 2010. This shows that there have been more journals focusing on airline disruption management problems in recent decades. There were more choices of journals for article publication after 2010 than before 2010.

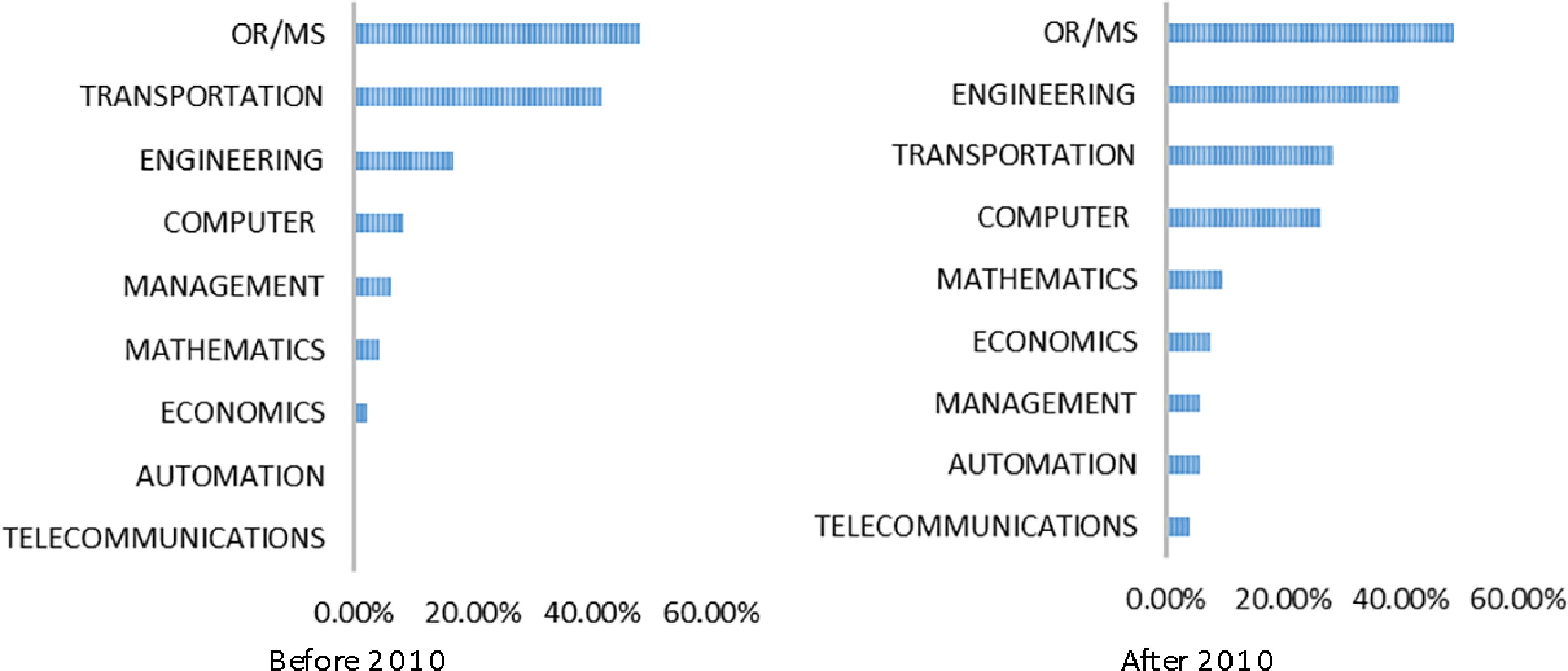
Based on the category lists on the InCites Journal Citations Report website^[15], the numbers of published articles in various categories were statistically compared during both periods. Figure 2 shows the statistical results, where the vertical axis represents the research field and the horizontal axis represents the literature rate in each field, i.e., the number of published articles in the corresponding field divided by the total number of articles. The left graph in Fig. 2 corresponds to the period before 2010, and the right graph refers to the period after 2010. As we can see in Fig. 2, there are eight fields related to airline disruption management. 'OR/MS' refers to the category of 'OPERATIONS RESEARCH & MANAGEMENT SCIENCE' on the website^[15]; 'TRANSPORTATION' includes both 'TRANSPORTATION' and 'TRANSPORTATION SCIENCE & TECHNOLOGY'; and 'ENGINEERING' is a collective name for the 'INDUSTRIAL', 'ELECTRICAL & ELECTRONIC', 'CIVIL', and 'MULTIDISCIPLINARY' areas. As some journals belong to more than one category, the papers published in the corresponding journals contribute to more than one research field. By comparing the two graphs in Fig. 2, we can easily find the differences between the two periods. First, six fields were involved before 2010, while eight fields were involved after 2010. Second, most studies before 2010 were published in journals in two research fields, while the range after 2010 extended to four research fields: 'OR/MS', 'ENGINEERING', 'TRANSPORTATION' and 'COMPUTER'. It is noted that the research field 'ENGINEERING' has concentrated more on this area than 'TRANSPORTATION'. This clearly illustrates that studies of airline disruption management problems have gained more influence, especially in the 'ENGINEERING' and 'COMPUTER' research fields.

Figure 2.  Number of published articles in various research fields.

DownLoad: Full-Size Img PowerPoint

Statistics on various resources of airline operations

Clausen et al.^[8] collected and analyzed 48 studies on all types of airline disruption management problems from journal papers, conference proceedings, working papers, and technical reports, while we found 53 published papers among only journal papers and conference proceedings in the databases of ISI's Web of Science, ScienceDirect, and the Wiley Online Library. This shows that the total number of studies on airline disruption management problem has increased. We will display and compare the statistical results based on different resources in airline recovery.

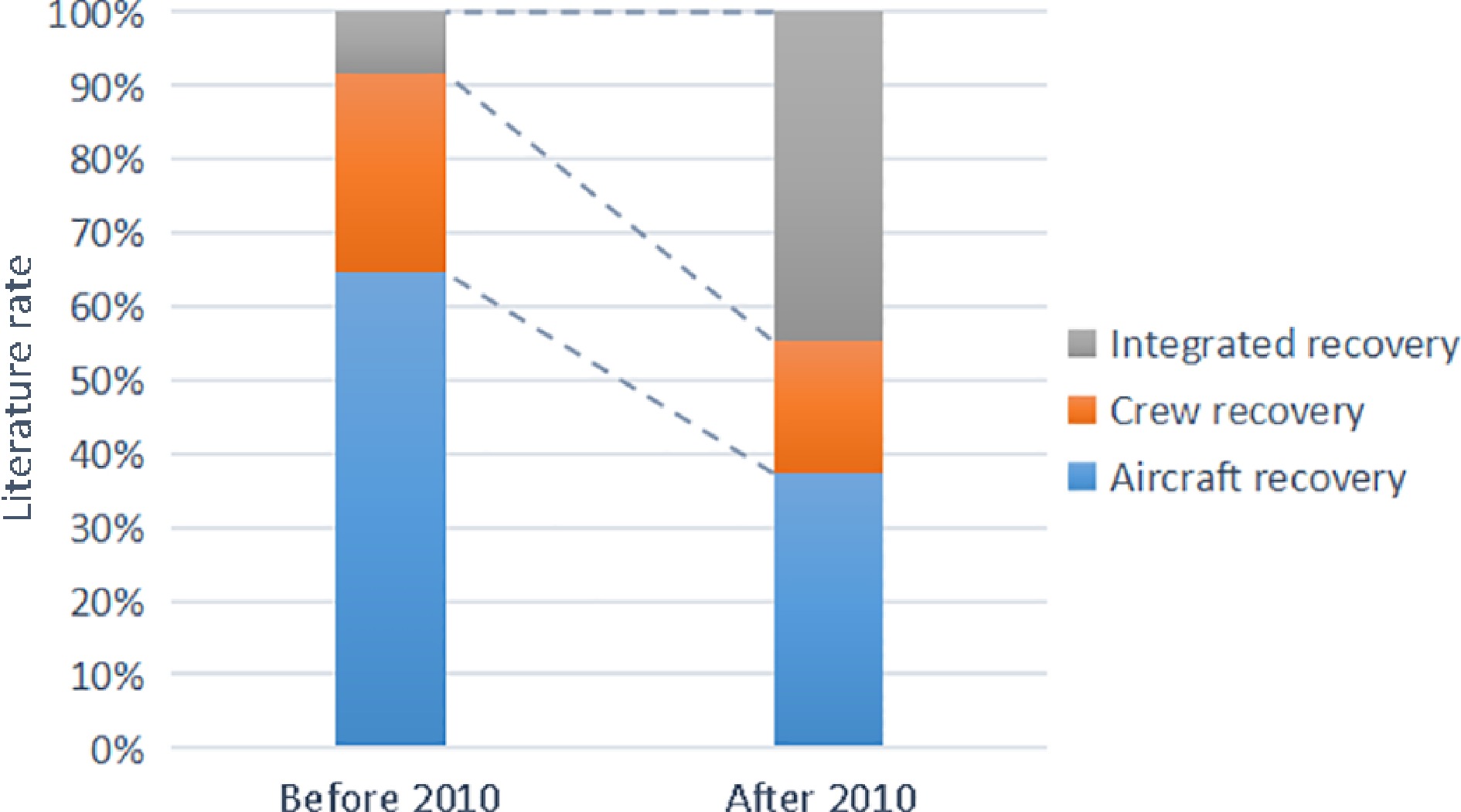
Generally, airline disruption management is related to three types of resources: aircraft, crew, and passengers. Passengers are special because they are also the object of airline service. Clausen et al.^[8] and most studies divide the literature into three sets according to the related recovery resources. The three sets refer to three research topics: aircraft recovery, crew recovery, and integrated recovery. We also provide simple literature statistics on the three topics and compare them with those of Clausen et al.^[8] in Fig. 3. The vertical axis represents the literature rates of the three topics.

Figure 3.  Literature rates of different recovery resources before and after 2010.

DownLoad: Full-Size Img PowerPoint

As can be seen in Fig. 3, before 2010, more than 60% of papers focus on aircraft recovery, and less than 10% of papers concentrate on integrated recovery. After 2010, the rate of papers on integrated recovery increased to more than 40%, which is almost the same as that of aircraft recovery. Integrated recovery involves multiple resources during airline disruption recovery, and the complexity of the studies is far greater than that of single-resource recovery. Therefore, there are two reasons why integrated recovery after 2010 is more popular than before 2010. The first reason may be due to practical airline demands. Passengers are not only the service objects of airlines but also the main source of profits for airlines. Therefore, the primary purpose of airline disruption recovery is to deliver passengers to their destinations with suitable aircraft and crews. Approximately 90% of studies include passenger recovery in the research set of integrated recovery. The second reason may be due to the recent development of computer hardware and software technology. The computing efficiency is greatly improved, and it can meet the complex computing requirements of integrated recovery.

Trends in the number of studies by year and type of recovery resources

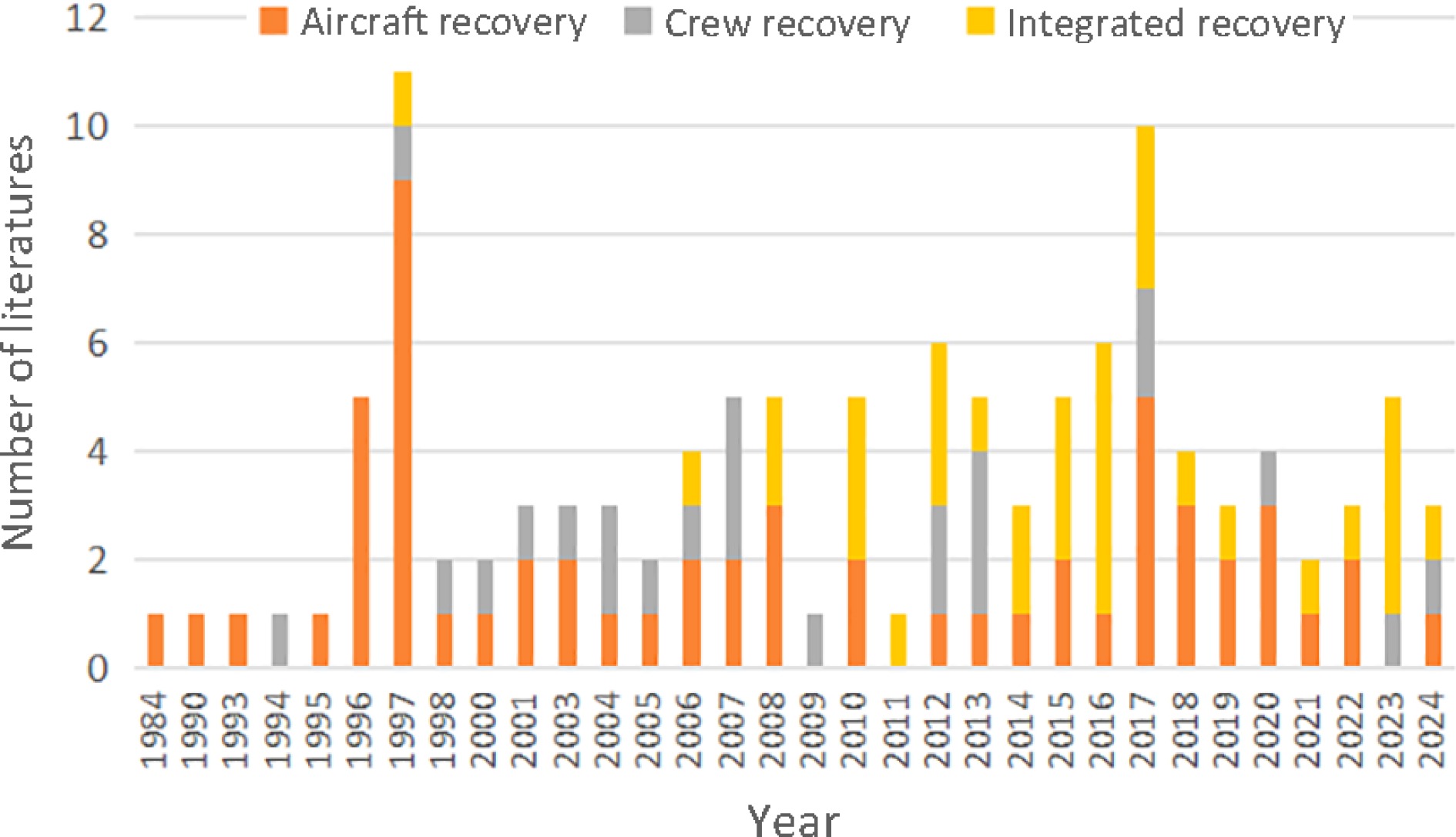
Figure 4 provides information about the number of studies during the years 1984−2024 and the types of recovery resources considered by these papers.

Figure 4.  Trends in the number of studies over time and the type of recovery resources.

DownLoad: Full-Size Img PowerPoint

Figure 4 shows that the number of studies peaks in two years: 1997 and 2017. The trends can be divided into four segments by the two peaks. First, during the almost 12 years from 1984 to 1995, there were only five papers in four journals and one technical report. Second, in 1996 and 1997, the number of papers reached a peak of 16 papers. Two research groups led by Yan and Yu contributed nine papers to this peak. Then, between 1998 and 2005, the number of published papers was only two or three each year. Finally, between 2006 and 2019, except for 2017, the number of papers fluctuated greatly, with an average number of four or five per year. Since this time, on average, there has been a significant upward trend in the number of papers on airline disruption management recovery. Note that 2017 is the year with the largest number of published papers, 20 years after the previous peak. This shows an increase in researchers' attention to the area of airline disruption management in recent years.

Next, the trends of the research topic of resource recovery are the focus. (1) Aircraft recovery was the initial focus of airline disruption management in Teodorović & Guberinić^[4]. It is interesting that there were only three published papers during the 10 years from 1984 to 1993. The number of papers increased explosively in 1997 and then largely stabilized at one or two per year. During the last three years, since 2017, the number of papers each year has increased to an average of three. (2) The research on crew recovery started in 1994 and maintained an average annual publication rate of one paper between 1997 and 2013. After 2014, the number of crew recovery publications clearly decreased. (3) In terms of integrated recovery, we can see in Fig. 4 that there are almost no publications before 2005, except for one Ph.D. thesis^[13]. After 2006, however, the studies increased year by year and reached a peak in 2016. This shows that integrated recovery has attracted more scholars' attention in recent decades.

Statistics on disruptions and recovery options of airline operations

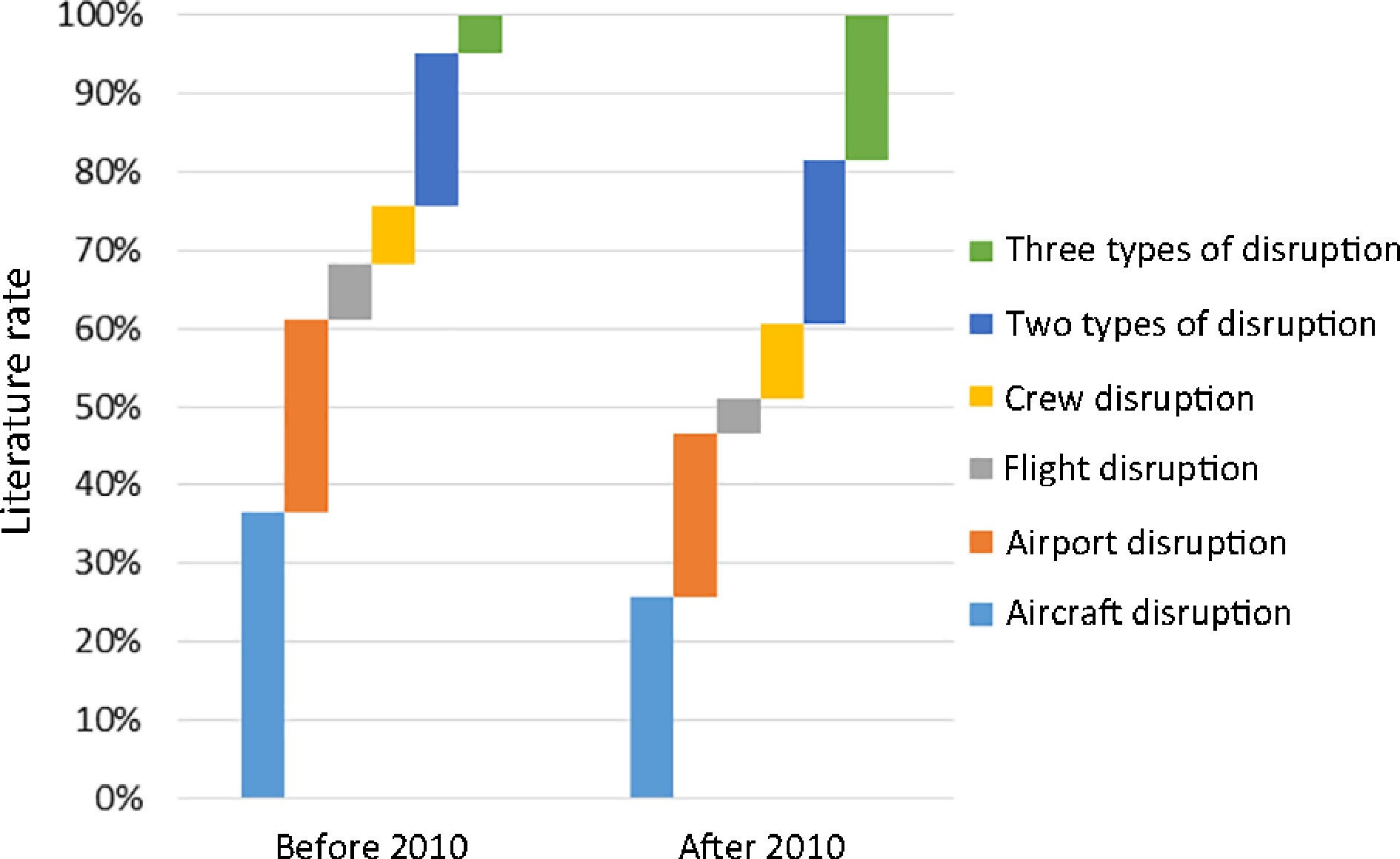
Airline schedules are often disrupted by internal or external factors, such as breakdown maintenance, severe weather, crew reassignments, and air traffic control. It will result in the shortage of some resources, such as aircraft, airports, crews, flights, and even simultaneous disruption of multiple resources, over a period of time. Figure 5 shows the comparison of disruption types considered by these papers before 2010 and after 2010. The vertical axis represents the literature rates of various disruption types. 'Aircraft disruption' refers to the literature that studies airline recovery under a shortage of aircraft for original schedules by a period of time due to breakdown maintenance or ground delay programs for air traffic control. 'Airport disruption' represents the papers that study airline recovery under airport closure for a period, often resulting from severe weather. 'Flight disruption' mainly refers to studies focusing on recovery under delay and cancellation of several flights. 'Crew disruption' mainly includes airline recovery studies under crew misconnection due to their late arrival, insufficient rest, crew duty exceeding, crew unassignment, and crew augmentation. Additionally, 'two types of disruption' and 'three types of disruption' refer to the problems where two and three types of resources are disrupted simultaneously and are considered in the paper.

Figure 5.  Literature rates of disruption types before and after 2010.

DownLoad: Full-Size Img PowerPoint

From Fig. 5, we know that approximately 75% of papers focused on the recovery problem under a single type of disruption before 2010, while the rate of these papers decreased to less than 60% after 2010. In detail, the rates of papers focusing on 'aircraft disruption', 'airport disruption', and 'flight disruption' have decreased. However, more studies have focused on the recovery problem under multiple types of disruptions after 2010. It is the most obvious that the rate of the 'three types of disruption' apparently increased from less than 5% before 2010 to almost 20% after 2010. It is noted that the rates of 'two types of disruption' are almost the same before and after 2010, as shown in Fig. 5. Interestingly, we found that more papers studied the recovery problem under aircraft and flight disruption before 2010, but more papers focused on the recovery problem under aircraft and airport disruption after 2010. It is obvious that 'airport disruption' is much more complicated than 'flight disruption'. Overall, we can conclude from disruption types that airline disruption management is more complicated than before.

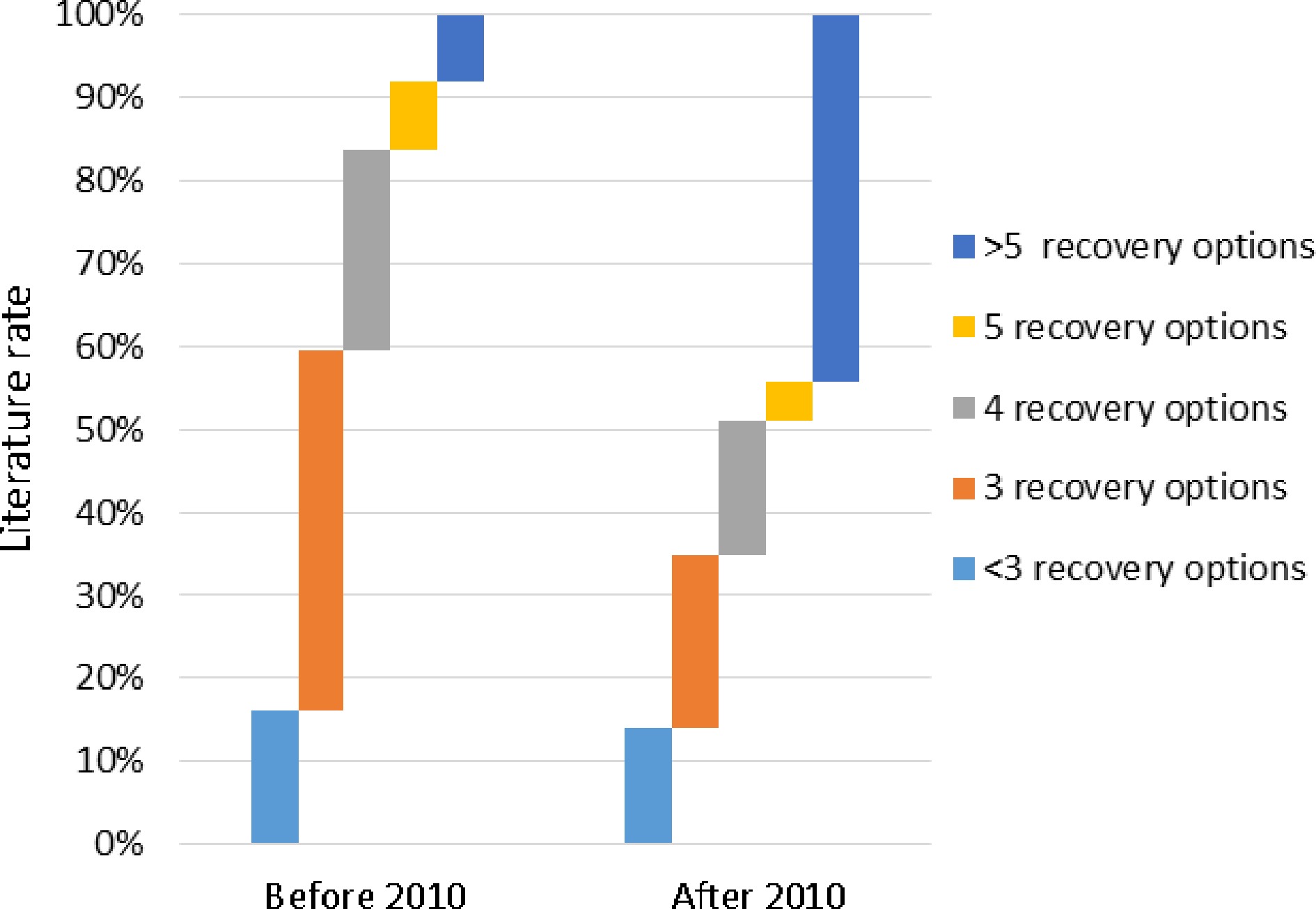
Faced with more complicated disruptions, more recovery measures should be taken to promote the recovery of original schedules. Recovery options generally vary for different resources. The recovery options for flights mainly include flight swaps, flight delays, and flight cancellations. The recovery options for aircraft are composed of fleet substitution, cruise speed control, using surplus aircraft, and ferrying. The recovery options for crews mainly include crew swaps, reserve crews, and crew deadheading. Finally, the recovery options for passengers refer to passenger itinerary rerouting, and ticket refunding. Figure 6 shows a simple statistical comparison given the number of recovery options. The vertical axis represents the literature rates of various numbers of recovery options. From Fig. 6, we know that the rate of papers considering not over five recovery options decreased from more than 90% before 2010 to approximately 55% after 2010. This indicates that more recovery options must be taken into account in recent studies.

Figure 6.  Literature rates of recovery options before and after 2010.

DownLoad: Full-Size Img PowerPoint

From Figs 5 & 6, it was found that there is no direct correspondence between the number of disruption types and the number of recovery options, but there is an obvious relationship between some disruption types and the number of recovery options. For example, although airport disruption is a single type of disruption, airlines should take more recovery measures faced with such severe disruption. Additionally, from Figs 3 & 6, we also found that the number of recovery options is closely related to the recovery resources. It is noted that the literature rate of 'integrated recovery' is almost the same as the rate of '> 5 recovery options', i.e., integrated recovery of several resources can only be realized by more recovery measures.

Summary of the statistical analysis

A summary of the present findings based on the statistics is as follows:

(1) Twenty-eight journals published at least one paper on airline disruption management problems after 2010, which is more than before 2010, with 18 journals.

(2) The three journals with the highest number of published papers after 2010 are 'Computers & Operations Research', 'Transportation Science', and 'Journal of Air Transport Management'.

(3) More research fields have paid close attention to the area of airline disruption management after 2010, especially in the 'ENGINEERING' and 'COMPUTER' areas, in addition to 'OR/MS' and 'TRANSPORTATION' before 2010.

(4) Integrated recovery has attracted more attention; the literature rate increased from less than 10% before 2010 to more than 40% after 2010.

(5) There are two peaks in the number of papers per year: in 1997 and in 2017.

(6) The number of studies on integrated recovery increased year by year after 2006 and reached a peak in 2016.

(7) More studies focus on airline recovery problems under the occurrence of multiple disruption types after 2010, and more recovery measures are also considered in the existing literature along with the complexity of disruption.

Literature breakdown and analysis

According to the classification that was applied in "Statistics on various resources of airline operations" and "Trends in the number of studies by year and type of recovery resources", we will describe the studies published during the years 2010−2024 in detail. Aircraft recovery refers to the literature on aircraft recovery, Crew recovery presents the literature on crew recovery, and Integrated recovery describes the literature on integrated recovery. Therefore, the first two sections focus on the recovery of single resources. The last section concentrates on the integrated recovery of multiple resources.

Key information related to the airline disruption management problem proposed in the present reviewed papers is summarized in Tables 1−6, with Tables 1 & 2 for aircraft recovery, Tables 3 & 4 for crew recovery, and Tables 5 & 6 for integrated recovery. The information in Tables 1, 3 & 5 includes the following common attributes: 'multiobjective', 'model'. The attributes of 'objective', 'single', and 'multi' mean the paper develops a mathematical model with single or multiple objectives, respectively. The attributes of 'model', 'LP' means linear programming, 'IP' means integer programming, 'CP' means constraint programming, and 'MICQ' means mixed-integer conic quadratic. The information in Tables 2, 4 & 6 includes the following common attributes: 'solution methodology', 'data', 'data dimension', and 'solution time (sec)'. The attributes of 'data', 'RL' means the paper uses real-world instances to test the performance of the proposed model and solution methodology. The attribute of 'data dimension', aims to display the largest instance scale in the computation experiments.

Table 1.  The first part of the proposed method overview for aircraft recovery.

	Network	Cancel	Delay	Aircraft swap	Cruise speed	Fleet	Objective	Model	Objectives
Chen et al.[29]	NA	NO	YES	YES	NO	Single	Multi	nonlinear	Flight non-connection, duty swap, delay time, delay number, delay number over 30 min
Liu et al.[31]	NA	NO	YES	YES	NO	Multi	Single	Nonlinear	Operation, delay, passenger cost
Babić et al.[32]	NA	YES	YES	YES	NO	Multi	Single	Nonlinear	Max revenue minus operational and disturbance costs
Liu et al.[30]	NA	NO	YES	YES	NO	Single	Multi	Nonlinear	Delay time, duty swap, variance of flight delay time, number of delayed flight, number of long-delayed flight
Gao et al.[36]	NA	NO	YES	NO	NO	Single	Multi	Nonlinear	Weighted flight delay time
Mou et al.[37]	NA	YES	YES	YES	NO	Multi	Multi	Nonlinear	Delay minutes, delay, and cancellation cost
Aktürk et al.[38]	CN	NO	YES	YES	YES	Multi	Single	Conic IP	Delay, deadhead, additional fuel and carbon emission, passengers spilled cost
Vos et al.[17]	TN	YES	YES	YES	NO	Single	Single	LP	Operation, delay, cancellation, aircraft ground cost
Guimarans et al.[33]	NA	NO	YES	YES	NO	Single	Single	CP	Delay time
Xu et al.[22]	TBN	YES	YES	YES	NO	Single	Single	IP	Delay, cancellation cost
Hu et al.[24]	CN	YES	YES	YES	NO	Multi	Multi	IP	Min delay and cancellation cost, maximal flight delay time, min the number of swapped aircraft
Wu et al.[25]	CN	YES	YES	YES	NO	Single	Single	IP	Delay time
Wu et al.[45]	CN	YES	YES	YES	NO	Multi	Single	IP	Delay, cancellation cost
Wu et al.[46]	CN	YES	YES	YES	NO	Multi	Single	IP	Delay, cancellation cost
Zhang[27]	CN	YES	YES	YES	NO	Single	Single	IP	Cancellation, aircraft assignment, terminal balance violation cost
Bouarfa et al.[40]	NA	NA	NA	NA	NO	NA	NA	NA	NA
Khaled et al.[41]	NA	YES	YES	YES	NO	Single	Multi	IP	Operation recovery cost, number of flight changed, number of impacted airports
Liang et al.[28]	CN	YES	YES	YES	NO	Multi	Single	IP	Flight cancellation, route cost
Lin et al.[34]	NA	NO	YES	YES	NO	Single	Single	Nonlinear	Delay time
Wang et al.[42]	NA	YES	YES	YES	NO	Multi	NA	NA	NA
Şafak et al.[39]	NA	YES	YES	YES	YES	Multi	Single	MICQ	Max revenue minus fuel burn, passenger spilled, flight arrival tardiness, crew service, aircraft swap cost
Vink et al.[18]	TN	YES	YES	YES	NO	Multi	Single	Mixed IP	Operation and disruption cost
Pei et al.[43]	NA	NO	YES	YES	NO	Multi	NA	NA	NA
Lee et al.[19]	TN	YES	YES	YES	YES	Multi	Single	Nonlinear	Expected recovery cost
Ji et al.[47]	NA	YES	YES	NO	NO	Multi	Single	Nonlinear	Delay time
Huang et al.[20]	TN	YES	YES	YES	NO	Multi	Single	IP	Retimed, cancelled or assigned cost
Şi̇mşek et al.[48]	NA	YES	YES	YES	YES	Multi	Single	Nonlinear	Fuel consumption and CO2 emission cost
Zang et al.[21]	TN	YES	YES	YES	NO	Multi	Single	Nonlinear	Delay, cancellation cost

 | Show Table

DownLoad: CSV

Table 2.  The second part of the proposed method overview for aircraft recovery.

	Delay cost	Aircraft maintenance	Airport congestion	Solution method	Data	Data dimension		Solution time (s)
						AC	Flight
Chen et al.[29]	NA	NO	NO	Hybrid multi-objective genetic algorithm	RL	7	70	600
Liu et al.[31]	Linear	NO	NO	Hybrid particle swarm optimization heuristic	RL	NA	34	236
Babić et al.[32]	Linear	YES	NO	Heuristic	JAT Airways	9	47	NA
Liu et al.[30]	NA	NO	NO	Hybrid multi-objective genetic algorithm	RL	7	84	450
Gao et al.[36]	NA	NO	YES	Polynomial algorithm	Generated	4	8	NA
Mou et al.[37]	Linear	NO	NO	Polynomial algorithm	Generated	5	10	NA
Aktürk et al.[38]	Nonlinear	YES	YES	CPLEX	An airline in the US	60	207	248.4
Vos et al.[17]	Nonlinear	YES	NO	Selection algorithm	Kenya Airways	43	NA	600
Guimarans et al.[33]	NA	NO	NO	Large neighbourhood search	RL	48	294	205.514
Xu et al.[22]	Linear	NO	NO	CPLEX	RL	60	254	949.7
Hu et al.[24]	Linear	NO	NO	Heuristic based on ε-constraints and neighbourhood search	A major Chinese airline	104	401	1200
Wu et al.[45]	NA	NO	NO	CPLEX	RL	12	140	7.02
Wu et al.[25]	Linear	NO	NO	CPLEX	RL	30	215	NA
Wu et al.[46]	Linear	NO	NO	CPLEX	RL	27	162	286.6
Zhang[27]	Linear	YES	NO	Heuristic + CPLEX	RL	44	638	150
Bouarfa et al.[40]	NA	NA	NA	Multi-agent system approach	NA	NA	NA	NA
Khaled et al.[41]	NA	YES	NO	ε-Constraints + CPLEX	RL	11	111	30
Liang et al.[28]	Linear	YES	YES	Column generation + CPLEX	RL	44	638	356.13
Lin et al.[34]	NA	NO	NO	Fast variable neighbourhood search	RL	12	70	0.3
Wang et al.[42]	NA	YES	NO	Simulation	RL	628	5071	NA
Şafak et al.[39]	nonlinear	NO	NO	CPLEX	United Airlines	81	300	8074
Vink et al.[18]	Nonlinear	YES	NO	Selection algorithm	An airline in the US	100	600	44
Pei et al.[43]	NA	YES	NO	AHP + algorithm	A Chinese airline	29	92	NA
Lee et al.[19]	Nonlinear	NO	YES	Look-ahead approximation and sample average approximation	RL	NA	852	300
Ji et al.[47]	NA	NO	NO	Build-in flight feasibility verification algorithm	RL	NA	300	14.69
Huang et al.[20]	NA	NO	NO	Iterative copy generation algorithm	Nine RL scenarios	4-162	789	0.5-855
Şi̇mşek et al.[48]	NA	NO	Yes	Aircraft Swapping and Search Algorithm	Bureau of Transportation Statistics (2021)	NA	NA	NA
Zang et al.[21]	Linear	YES	YES	Decision-decomposition-based algorithm	Four Chinese airlines	733	2,877	23.82

 | Show Table

DownLoad: CSV

Table 3.  The first part of the overview of proposed methods for crew recovery.

	Network	Fixed f	Cancel f	Delay f	Crew swap	Objective	Objectives
AhmadBeygi et al.[49]	SP	YES	NO	NO	YES	Single	Pairing cost minus flight dual contribution
Chang et al.[50]	NA	NO	YES	NO	YES	Multi	Number of deadhead trip, unconnected flight, schedule changes and affected crews
Fang et al.[51]	NA	YES	NO	NO	YES	Multi	Deviation cost of flight time and duty time
Liu et al.[52]	SC	NO	YES	NO	YES	Single	Number of uncovered flights
Luo et al.[59]	SP	YES	NO	NO	YES	Single	Pairing cost
Bayliss et al.[55]	NA	NO	NO	YES	NO	Single	Expected crew delay
Chen et al.[53]	NA	YES	NO	NO	YES	Multi	Number of crew changes, number of duty changes, maximal duty changes, largest changed flight time, derivation of the changed duties, derivation of changed flight time
Bayliss et al.[56]	NA	NO	YES	NO	YES	Single	Cancellation
Bayliss et al.[57]	NA	NO	YES	YES	YES	Single	Delay and cancellation
Wen et al.[60]	DN	YES	NO	NO	NO	Single	Robustness-related cost
Herekoğlu et al.[61]	NA	NO	YES	YES	YES	Multi	Assignment cost, swapping cost, deadheading costs, cancellation costs, delaying costs, penalties
Zhong et al.[62]	NA	NO	YES	NO	YES	Multi	Deviation of duty time, total recovery cost

 | Show Table

DownLoad: CSV

Table 4.  The second part of the overview of proposed methods for crew recovery.

	Solution method	Data	Data dimension				Solution time (s)
			Aircraft	Crew	Flight	Recovery period (d)
AhmadBeygi et al.[49]	CPELX	A major US hub-and-spoke carrier	NA	NA	329	1	2065
Chang et al.[50]	Genetic algorithm	An international Taiwanese airline	NA	70	628	18	600
Fang et al.[51]	Hybrid simulated annealing	Domestic airlines	NA	87	342	NA	195.04
Liu et al.[52]	Simulated annealing	A major airline in the US	NA	482	1069		236
Luo et al.[59]	Primal-dual sub-problem simplex method in a branch-and-price framework	Three airlines	NA	NA	NA	30	NA
Bayliss et al.[55]	Greedy heuristic	Generated	37	120	300	1	1400
Chen et al.[53]	Evolutionary algorithm	A short-haul airline in Taiwan		270	1048	14	1080
Bayliss et al.[56]	Heuristic + CPLEX	Generated	37	148	243	3	3600
Bayliss et al.[57]	heuristic + CPLEX	Generated	74	209	566	2	600
Wen et al.[60]	Customized column generation based solution algorithm	An airline in Hong Kong	NA	NA	98	3	NA
Herekoğlu et al.[61]	Column generation-based solution approach	A major European airline company	400	13500	1873	3	5438
Zhong et al.[62]	Ad-hoc particle swarm optimization -based optimizer	Vari Flight Company	NA	NA	166	4	NA

 | Show Table

DownLoad: CSV

Table 5.  The first part of the overview of proposed methods for integrated recovery.

	Aircraft	Crew	Passenger	Net-work	Cancel	Delay	Aircraft swap	Fleet	Cruise speed	Objective	Model	Objectives
Eggenberg et al.[75]	YES	NO	YES	CN	YES	YES	YES	Multi	NO	Single	IP	Passengers delay, cancellation cost
Jafari et al.[68]	YES	NO	YES	NA	YES	YES	YES	Multi	NO	Single	Nonlinear	Aircraft assignment, flight delay, flight cancellation, passenger disruption cost
Bisaillon et al.[11]	YES	NO	YES	NA	YES	YES	YES	Multi	NO	Single	NA	Aircraft and flight operation, passenger disruption cost, constraints violation
Artigues et al.[9]	YES	NO	YES	NA	NA	NA	NA	NA	NA	NA	NA	NA
Mansi et al.[78]	YES	NO	YES	TBN	YES	YES	YES	Multi	NO	Single	NA	Aircraft and flight operation, passenger disruption cost, constraints violation
Petersen et al.[86]	YES	YES	YES	CN	YES	YES	YES	Multi	NO	Single	IP	Flight delay and cancellation, aircraft assignment, crew pairing and deadheading, passenger delay and unassignment cost
Jozefowiez et al.[76]	YES	NO	YES	NA	YES	YES	YES	Multi	NO	Single	NA	Aircraft and flight operation, passenger disruption cost, constraints violation
Brunner [85]	YES	YES	YES	NA	YES	YES	YES	NA	NO	Single	Mixed IP	Flight arrival and departure delay, flight cancellation, crews' and passengers' misconnection cost
Sinclair et al.[80]	YES	NO	YES	TN	YES	YES	YES	Multi	NO	Single	NA	Aircraft and flight operation, passenger disruption cost, constraints violation
Hu et al.[35]	YES	NO	YES	TBN	YES	YES	YES	Multi	NO	Single	IP	Flight delay, passenger transiting, passenger refunding cost
Maher[87]	YES	YES	YES	CN	YES	YES	YES	Multi	NO	Single	IP	Flight delay and cancellation, crew deadheading, and passenger reassignment cost
Zhang et al.[65]	YES	YES	NO	TN	YES	YES	YES	Multi	NO	Single	IP	Flight delay and cancellation, crew misconnection, aircraft and crew swap cost
Arıkan et al.[88]	YES	NO	YES	CN	NO	YES	YES	Multi	YES	Single	Conic IP	Aircraft delay, passengers delay, spill cost, swap cost, and increased fuel cost
Hu et al.[81]	YES	NO	YES	CN	YES	YES	YES	Multi	NO	Single	IP	Passengers' delay, reassignment, refund cost
Maher[66]	YES	YES	NO	CN	YES	YES	YES	Single	NO	Single	IP	Flight delay and cancellation, reserve crew, crew duty and deadhead cost
Sinclair et al.[79]	YES	NO	YES	TN	YES	YES	YES	Multi	NO	Single	NA	Aircraft and flight operation, passenger disruption cost, constraints violation
Zhang et al.[77]	YES	NO	YES	TN	YES	YES	YES	Multi	NO	Single	NA	Aircraft and flight operation, passenger disruption cost, constraints violation
Arıkan et al.[88]	YES	YES	YES	CN	YES	YES	YES	Multi	YES	Single	conic IP	Flight cancellation, aircraft ferrying, crew deadheading, passenger delay, reallocation and refund, additional fuel cost, constraints violation
Marla et al.[72]	YES	NO	YES	TN	YES	YES	YES	Multi	YES	Single	IP	Flight delay and cancellation, aircraft swap, passenger disruption, additional fuel cost
Santos et al.[73]	YES	NO	YES	CN	NO	YES	YES	Multi	NO	Single	Mixed IP	Additional operation, passenger disruption cost
McCarty et al.[64]	NO	NO	YES	CN	NO	YES	YES	NA	NO	Single	Mixed IP	Passengers' expected delay cost
Yang et al.[82]	YES	NO	YES	CN	YES	YES	YES	Multi	NO	Multi	IP	Airline recovery, passenger uitility cost
Yeti̇moğlu et al.[74]	YES	NO	YES	CN	YES	YES	NO	NA	YES	Single	Nonlinear	Revenue - fuel and CO2 emission cost - overnight passenger cost - spilled passenger cost.
Evler et al.[89]	YES	YES	YES	NA	YES	YES	YES	Multi	NO	Single	Mixed IP	Operating and delay cost, cancel cost, connection cost, cost of assigning turnaround recovery options
Xu et al.[90]	YES	YES	YES	CN	YES	YES	YES	Multi	NO	Single	Mixed IP	Cost of flight cancellation, delay, crew deadhead and unassigned passengers
Zhao et al.[83]	YES	NO	YES	TN	YES	YES	YES	Single	NO	Single	Mixed IP	Disruption cost, passenger delay cost, curfew violation cost, cancel cost.
Cadarso et al.[92]	YES	NO	YES	TN	YES	YES	YES	Multi	YES	Single	Mixed IP	Flight operating cost, extra fuel consumption cost, flight delay cost, passenger reaccommodation cost, passenger delay cost, crew cost, penalizes aircraft changes
Ding et al.[91]	YES	YES	YES	TN	YES	YES	YES	NA	YES	Single	Mixed IP	Flight cancellation cost, passenger delay cost, external link cost, additional fuel cost and following schedule cost
Chen et al.[84]	YES	NO	YES	NA	YES	YES	YES	NA	NO	Multi	IP	The total delay cost of each flight, the sum of the passenger delay time of each flight

 | Show Table

DownLoad: CSV

Table 6.  The second part of the overview of proposed methods for integrated recovery.

	Delay cost	Aircraft maintenance	Airport congestion	Solution method	Data	Data dimension					Solution time (s)
						AC	Flight	Crew	Passenger	Passenger itinerary
Eggenberg et al.[75]	Linear	YES	NO	Column generation	Thomas Cook Airlines	100	760	NA	30000	NA	3603
Jafari et al.[28]	Linear	NO	NO	Lingo	Swedish domestic airline	13	100	NA	2236	8	NA
Bisaillon et al.[11]	Linear	YES	YES	Large neighbourhood search	2009 ROADEF Challenge	618	2178	NA	NA	29151	600
Artigues et al.[28]	Linear	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
Mansi et al.[78]	Linear	YES	YES	Two stage heuristic	2009 ROADEF Challenge	618	2178	NA	NA	29151	600
Petersen et al.[86]	Linear	YES	NO	Bender decomposition, column generation	Hub-and-spoke airline in the US	NA	800	NA	NA	NA	2407
Jozefowiez et al.[76]	Linear	YES	YES	Three stage	2009 ROADEF Challenge	618	2178	NA	NA	29151	600
Brunner[85]	Nonlinear	NO	NO	CPLEX	American Airlines	NA	71	26	651	651	NA
Sinclair et al.[80]	Linear	YES	YES	Large neighbourhood search	2009 ROADEF Challenge	618	2178	NA	NA	29151	600
Hu et al.[35]	Nonlinear	NO	NO	CPLEX	A major airline in China	188	628	NA	NA	NA	106
Maher[87]	Linear	NO	NO	Column and row generation	RL	48	262	79	28492	NA	1800
Zhang et al.[65]	Linear	YES	NO	Iteration heuristic + CPLEX	Regional airline in the US	70	351	134	NA	NA	72.418
Arıkan et al.[88]	Linear	NO	NO	CPLEX	Airline in US	NA	1429	NA	NA	NA	142
Hu et al.[81]	Linear	NO	NO	GRASP	A major airline in China	87	340	NA	NA	NA	600
Maher[66]	Linear	NO	NO	Column and row generation	RL	123	441	182	NA	NA	1200
Sinclair et al.[79]	Linear	YES	YES	Column generation	2009 ROADEF Challenge	618	2178	NA	NA	29151	1385
Zhang et al.[77]	Linear	YES	YES	Three stage	2009 ROADEF Challenge	618	2178	NA	NA	29151	600
Arıkan et al.[88]	Nonlinear	NO	NO	CPLEX	A major U.S. airline	402	1254	NA	NA	NA	1212.4
Marla et al.[72]	Linear	NO	NO	Xpress	A major European airline	NA	250	NA	NA	NA	120
Santos et al.[73]	Nonlinear	NO	YES	CPLEX	Kenya airways	45	140	NA	10000	NA	3600
McCarty et al.[64]	Linear	NO	NO	Benders Decomposition + CPELX	Delta Airlines	NA	NA	NA	200	15	93.9
Yang et al.[82]	Linear	NO	NO	Genetic algorithm	A major airline in China	59	209	NA	24860	NA	11
Yeti̇moğlu et al.[74]	NA	NO	NO	Novel math-heuristic algorithm	A major airline in America	53	208	NA	NA	2033	NA
Evler et al.[89]	Linear	YES	NO	Rolling horizon algorithm	Frankfurt airport	17	85	NA	NA	NA	45
Xu et al.[90]	Linear	NO	NO	Branch-and-cut solution method, large neighborhood search heuristic	One main legacy carrier in the US	NA	230	172	NA	NA	937.71
Zhao et al.[83]	Linear	YES	NO	Two-stage algorithm, rolling horizon approach	GE Aviation	73	207	NA	594	NA	NA
Cadarso et al.[92]	Linear	YES	YES	An original solution approach	A IBERIA airline	19	1074	NA	1204	32	600
Ding et al.[91]	Linear	YES	YES	Variable neighborhood search algorithm	Generated	50	NA	NA	NA	NA	0.359
Chen et al.[84]	Nonlinear	NO	NO	Genetic algorithm-II	A Chinese airline in Fuzhou airport	NA	NA	NA	1818	NA	14.57

 | Show Table

DownLoad: CSV

In Table 1, 'network' refers to the network type for aircraft recovery model construction: connection network (CN), time space network (TN), and time band network (TBN). The detailed network representation has been issued in Clausen et al.^[8]. 'Cancel', 'delay', 'aircraft swap', 'fleet', and 'cruise speed' refer to whether the paper considers the recovery options of flight cancellation, flight delay, aircraft swapping, swapping between multiple fleet types, and cruise speed control, respectively. In Table 2, 'delay cost' means, in the proposed model, the linear or nonlinear penalty for the departure or arrival delay time of each flight. 'Aircraft maintenance' and 'airport congestion' represent whether the paper considers the constraints of aircraft maintenance and airport capacity in the proposed model.

In Table 3, 'network' represents the network applied for the crew recovery model: set partition network (SP), set covering network (SC), and duty-based network (DN). 'Fixed f', 'cancel f', and 'delay f' refers to whether the crew recovery model includes the decision variables of flight delay and flight cancellation. 'Crew swap' refers to whether the paper considers the recovery options of crew swaps. In Table 5, the first three attributes, 'aircraft', 'crew', and 'passenger', represent the combination of several resources in the recovery problems.

Aircraft recovery

The aircraft recovery problem (ARP) has been acknowledged as the earliest research branch compared to crew and integrated recovery in the field of airline disruption management. In addition to the smaller number and simpler rules of aircraft compared to other resources, such as crews and passengers^[8], the core reason may be that aircraft are equipment, while crews and passengers are human beings. We can seek only a profit maximum or cost minimum in the ARP and can ignore the complicated psychology of human beings. This type of problem is exactly what operations research and optimization methods are good at addressing. As a classical optimization problem, there are typically two considerations in the ARP: a model formulation that accurately defines the detailed boundary of the problem and a solution methodology that shows how to obtain the solution to the problem. For this reason, categorizing aircraft recovery papers based on the model formulation and solution methodology is meaningful. Formally, these classifications are as given below. Tables 1 & 2 show the key information of the ARP literature in chronological order.

(1) Solution methodology based on network. Studies in this group are similar to most of the papers introduced in Clausen et al.^[8]. The problem is formulated with networks (connection networks, time-line networks, or time-band networks) and then solved by an exact algorithm and the CPLEX solver.

(2) Meta-heuristic studies. Studies in this category seek more efficient meta-heuristics to obtain satisfactory solutions to the ARP. Note that papers in this category give less attention to model formulation. Some papers do not even include an accurate model.

(3) Polynomial studies. Studies in this category aim to analyze the optimization characteristics of the ARP in certain special situations and to design polynomial algorithms for optimal or approximately optimal solutions.

(4) Other studies. Unlike the above groups, studies in this group consider some specific approaches to analyzing the ARP.

Solution methodology based on network

To date, the majority of publications use integer programming solution methods to solve the aircraft recovery problem. Integer programming models are generally formulated based on various networks. Related studies by the classification of network representation will be introduced, which have been described in Clausen et al.^[8] on network graphs and networks, i.e., time-space network, time-band network, and connection network.

Time-space network

The time-space network was first introduced by Yan & Yang^[16] for flight rescheduling and aircraft recovery problems. The main advantages of the network lie in the clear graphical representation of the flight network by the time-space node and relative arcs. Moreover, the idea of discretizing flight delay time can ingeniously transform the aircraft recovery problem to a network optimization problem with boundary constraints. However, the disadvantage of the time-space network is the majority of the decision variables due to the copies of flight delay arcs. It will lead to lower efficiency in computation time. Therefore, some studies focus on the dynamic recovery methodology based on a time-space network. It can not only reduce the recovery scale but also fit the practical dynamic character of airline disruption. For example, Vos et al.^[17] develop a dynamic modeling framework based on a parallel time-space network. Vink et al.^[18] presented an exact mathematical model for the proposed dynamic aircraft recovery problem. Lee et al.^[19] presented a stochastic reactive and proactive disruption management model that combines a stochastic queuing model of airport congestion to minimize the expected recovery costs. Huang et al.^[20] proposed a copy evaluation method and develop a solution approach to the Aircraft Recovery Problem by incorporating the method within an iterative process of copy generation and filtration. Zang et al.^[21] examined aircraft recovery problem from the viewpoint of balancing supply and demand across the airport time-space network through aircraft rotations between airports.

Time-band network

Compared to the time-space network, the time-band network plays an important role in reducing the number of flight arcs and corresponding decision variables. It divides the recovery time periods into several discrete time intervals. Of course, the core drawback of the time-band network is that the flight delay cost will be overestimated or underestimated, and even sometimes the rescheduled flight network is not feasible due to time connection failure unless the optimization result is fine-tuned. Xu & Han^[22] extend the time band network for aircraft recovery in a hub-and-spoke network and use a simplex group cycle approach to control the fight disruption scope and depth.

Connection network

In contrast to the few studies that construct integer models based on time-space or time-band networks, more studies prefer to use connection networks, which are most popular for airline scheduling, to formulate the aircraft recovery problem. The major advantage of this network is that it is more suitable for solving large-scale problems by combining column generation and bender decomposition algorithms. One disadvantage is that it is often used for single-objective optimization in airline disruption management. Zhu et al.^[23] establish a two-stage stochastic programming model based on a connection network, where the aircraft recovery time is not fixed. Hu et al.^[24] describe multiobjective mathematical programming and solve the proposed problem using heuristics instead of exact algorithms. Wu et al.^[25] develop a distributed computation algorithm^[26] to generate feasible flight routes for solving the integer programming model based on a connection network. Zhang^[27] introduces a two-stage heuristic to design an aircraft recovery network before using a set partition model. Liang et al.^[28] add the constraints of aircraft planning maintenance and the airport slot capacity to the connection network and then solve it using a column generation heuristic.

Meta-heuristics

As an airline is more concerned with recovery time efficiency than with the optimality of the recovery solution, it is more attractive to obtain a satisfactory recovery solution in a short CPU time than to obtain a near-optimal solution over a long time for real applications in the airline industry. Therefore, heuristics have often been applied in recent years for solving aircraft recovery problems, such as the genetic algorithm in Chen et al.^[29] and Liu et al.^[30], hybrid particle swarm in Liu et al.^[31], and neighborhood search algorithm in Babić et al.^[32], Guimarans et al.^[33] and Lin & Wang^[34].

Polynomial algorithms

Although the aircraft recovery problem has been proven NP-hard^[35], some studies still prefer to analyze optimization characteristics and design polynomial algorithms for some special cases of the problem. Gao et al.^[36] focus on flight rescheduling under large-scale flight delays considering flight delays and flight cancellations rather than flight swaps between different aircraft routings. Then, a polynomial algorithm is designed to obtain the optimal solution for the flight rescheduling problem. Mou & Zhou^[37] developed an uncertain programming model with chance constraints, where the uncertainty distribution of the aircraft delay time is given by experts. A recovery solution method is designed based on a stepwise-delay algorithm and the Hungarian algorithm. Hu et al.^[24] solved the aircraft recovery problem with the hierarchical-objectives programming model by a polynomial algorithm.

Other studies on aircraft recovery

In addition to common concerns of aircraft recovery, some studies focus on special solution approaches to analyze or solve the proposed problem. For example, Aktürk et al.^[38] and Şafak et al.^[39] propose a mathematical model, especially for considering cruise speed control in the aircraft recovery problem. Bouarfa et al.^[40] evaluated the performance of a multiagent system for disruption management in an airline operation control (AOC) department, and Khaled et al.^[41] established a multicriteria recovery framework based on a tail assignment model. Wang et al.^[42] applied a simulation method to analyze the performance of the aircraft recovery process. Pei et al.^[43] presented a data-driven method to solve the flight rescheduling problem based on AHP and heuristics.

Research findings

(1) More studies have started to focus on multiple-fleet aircraft recovery. Approximately 15 of 25 papers (more than 50%) studied multiple fleet aircraft recovery operations after 2010, while the rate was less than 23% before 2010 according to Clausen et al.^[8]. This makes the recovery model more complex due to aircraft swapping between different fleets.

(2) More studies have started to focus on multiple-objective programming to formulate the aircraft recovery problem. The model formulation in approximately six of 25 papers was developed with multiple objectives, while the number was no more than three of 31 papers before 2010. The reason is apparent. Before 2010, most solution methodologies for aircraft recovery were derived from the airline planning phase. Most model formulations were constructed for airline planning with a single objective. It can easily be solved with corresponding optimization techniques. However, due to the complexities of the real-time environment, it is difficult to use a single-objective model to accurately describe many needs of airlines. Therefore, some scholars have aimed to construct multiple-objective formulations to describe aircraft recovery problems.

(3) Almost all studies propose the common consumption that the aircraft recovery model does not consider the recovery measures of using surplus aircraft and ferrying aircraft. The assumption is realistic to some extent. Because aircraft are expensive equipment and rented instead of being bought by airlines, it is a waste of aircraft resources for airlines to leave aircraft idle or ferry spare aircraft. This is the reason why using surplus aircraft and ferrying aircraft are the last choices in actual airline recovery operations.

(4) Another common assumption in the airline recovery literature is that the flight delay cost is a linear function of delay time. This is slightly inconsistent with airline recovery practice since flight delay costs tend to be a nonlinear function of delay time^[44]. Some papers, such as
Aktürk et al.^[38], Vos et al.^[17], Şafak et al.^[39], and Vink et al.^[18], attempt to make changes to solve the actual airline operation problem.

(5) Airport capacity and aircraft dynamic fuel costs have begun to be considered in recovery models. This promotes disruption management more practically.

(6) More studies have started to solve aircraft recovery problems using heuristics. These heuristics include meta-heuristics and polynomial algorithms. Understandably, airline disruption management is an NP-hard problem^[35], and it pursues efficient computational time rather than optimization accuracy alone in real-time. Therefore, they have to use heuristics for practical efficient application.

(7) Aircraft recovery has begun to be considered in combinatorial optimization theory. Before 2010, more studies focused on the similarity of airline disruption management and airline scheduling. However, there are clear differences between them. The airline planning stage includes the scheduling of all resources, while airline disruption management is focused on minor changes, which reduces the problem scale and provides the possibility of optimization through theoretical analysis. Moreover, aircraft recovery is the most classical optimization problem in the field of airline disruption management. Optimization analysis of airline disruption management commonly starts from the aircraft recovery problem.

Crew recovery

Most papers continue previous research topics such as crew recovery after the occurrence of an airline disruption. These papers include AhmadBeygi et al.^[49], Chang^[50], Fang & Xia^[51],
Liu et al.^[52], and Chen & Chou^[53]. Other studies by Bayliss et al.^[54−57] focus on reserve crew scheduling to reduce flight delays and cancellations under various disruption situations. Tables 3 & 4 show the key information of the crew recovery literature in chronological order.

Classic crew recovery

AhmadBeygi et al.^[49] aimed to develop a crew pairing generator to support integrated airline planning, robust planning and automated recovery in addition to modeling nonlinear constraints and cost functions in crew scheduling. Multiple solutions for crew recovery are usually obtained from the genetic algorithm used by Chang^[50] and Chen & Chou^[53]. Another meta-heuristic for generating multiple solutions is the hybrid simulated annealing heuristic described in Fang & Xia^[51].

Reserve crew scheduling

Faced with airline disruptions, especially crew absence or delays, the application of reserve crews can promote the rapid recovery of airline schedules. To the best of our knowledge, airline reserve crew scheduling was first studied by Dillon & Kontogiorgis^[58]. In recent decades, reserve crew scheduling for airline recovery has mainly been studied in Bayliss et al.^[54−57]. Bayliss et al.^[54] focus on assigning the duty start time of reserve crews in case of the disruption of crew absence. Bayliss et al.^[55] extend the model for crew delay recovery. Bayliss et al.^[56] focus on reserve crew scheduling for both crew absence and delay. Bayliss et al.^[57] extend the influence of reserve crew scheduling on the probability of fight cancellation. Luo et al.^[59] introduce a development and improvement of the proposed models and solution approaches of Sabre for crew augmentation, initially for airline safety reasons during the crew pairing process. Wen et al.^[60] proposed a customized column generation based solution algorithm and on this basis, Herekoğlu & Kabak^[61] utilized a customized deep learning model to provide recovery actions as inputs. Zhong et al.^[62] designed an ad-hoc particle swarm optimization-based optimizer to solve Integrated Aircraft and Crew Recovery with Multi-objective and Priority efficiently.

Research findings

(1) In the field of airline disruption management, the crew is the other type of resource parallel to the aircraft. Crew recovery is also important for airline disruption management. Crew recovery research includes 13 papers published 14 years before 2010 and 12 papers published in the last 14 years. However, there have been research achievements in terms of problem extension and solution methodology.

(2) Although the scheduling of spare aircraft is uncommon due to the higher cost of calling a spare aircraft, studies of crew augmentation have begun to appear. After all, it is not as expensive to hire a spare crew as to hire an aircraft.

(3) In the existing literature for crew recovery, one common assumption is that the flight schedules have been recovered before the crew recovery process. Therefore, flights are generally fixed during the crew recovery process. The assumption is consistent with reality. Once the flight has been rescheduled in actual operation, only a few flights can be cancelled or delayed along with crew rescheduling. These assumptions are also considered by some papers.

(4) Although the number of papers focusing on crew recovery has not increased, more studies try to apply crew recovery problems with heuristics such as simulated annealing and genetic algorithms. There is only one paper^[63] that uses a combination method of column generation and a genetic algorithm according to Clausen et al.^[8], while there are no fewer than five such papers (nearly 50%) after 2010 according to our statistics.

Integrated recovery

Due to the complexity of airline disruption management in real situations, it is necessary to focus on the integrated recovery of multiple resources, which generally include aircraft, crew, and passengers. The integrated recovery models that are most constructed based on connection networks, aircraft routing and crew pairing are given in Clausen et al.^[8]. As another important recovery resource, passenger itinerary recovery is generally formulated as follows. Let F be the set of scheduled flights and I be the set of scheduled passenger itineraries. For each flight f∈F, the number of scheduled passengers NPass_f in flight f and the set of aircraft routes R(f) covering flight f are given. For each passenger itinerary i∈I, the ticket refunding cost refundc_i and the number of scheduled passengers NumP_i in itinerary i are given. We define the integer variable r_i as the number of passengers who refund their tickets and the binary variable z_i as 1 if itinerary i is disrupted and 0 otherwise. R(f) denotes the set of aircraft routes covering flight i. For each r∈R(f), Cap_r denotes the capacity of aircraft covering routing r, and the flight delay cost of flight f in route r is denoted by delayc_fr. We define the variable x_r, which is equal to 1 if aircraft route r is implemented and 0 otherwise. The objective (see Eqn (1)) aims to minimize the passenger delay and ticket refunding cost. The constraints promise that passengers can refund tickets only if their itineraries are disrupted (see Eqn (2)), and the reassignment for passengers cannot exceed the seat capacities of the aircraft (see Eqn (3)).

The model is commonly part of the integrated recovery model, instead of being applied alone for airline recovery. Additionally, there will be slight differences in various articles for recovery variants. For example, multifleet aircraft with different seat capacities and the cost of passengers transiting between different itineraries will be considered in some studies. It is noted that passenger itinerary recovery is seldom considered separately and is often one component of integrated recovery. Only McCarty & Cohn^[64] focus on the problem of performing passenger reallocation before itinerary misconnections occur. This is a proactive approach for passenger rerouting when facing uncertain itinerary delays rather than for post-disruption recovery.

According to the integration degree of the resources during the recovery process, integrated recovery publications can be analyzed in the following three categories: the integrated recovery of aircraft and crews, the integrated recovery of aircraft and passengers, and the integrated recovery of all three resources. Tables 5 & 6 show the key information of the integrated recovery literature in chronological order.

Integrated recovery of aircraft and crew

Zhang & Lau^[65] is one of the few studies that focus on the integrated recovery of aircraft and crew. The authors first generate routes of aircraft and crews based on a time-space network and then propose a novel two-stage heuristic to solve the integrated recovery problem. Maher^[66] represents a column-and-row generation algorithm framework to solve the integrated recovery of aircraft and crew problems based on Muter et al.^[67].

Integrated recovery of aircraft and passengers

The majority of publications formulate the integrated recovery of aircraft and passengers following the multicommodity network flow model. However, there are various solution methodologies for the problem, such as directly using commercial optimizers, applying large-scale optimization methods, and designing meta-heuristics. We classify the publications according to the solution methods used in these papers.

Direct method using a commercial optimizer

Jafari & Zegordi^[68] was the first attempt to establish a single objective model to represent and solve the integrated recovery of aircraft and passengers simultaneously based on aircraft rotations and passenger itineraries as an extension of the aircraft recovery formulation in Abdelghany et al.^[69]. Based on the time-band network in Bard et al.^[70], Hu et al.^[35] designed a reduced time-band network to study the integrated recovery of aircraft and passengers with itineraries along a single flight. Both Arıkan et al.^[71] and Marla et al.^[72] add the action of speed change in addition to common recovery actions in the integrated recovery of aircraft and passengers. Another study on the passenger recovery problem under airline delay management was reported by Santos et al.^[73] in daily flight operation at a hub airport under capacity limitations of the runway, taxiway and bay. Yeti̇moğlu & Aktürk^[74] worked on integrated networks at which aircraft routings and passenger itineraries are superimposed, and calculated the actual profit and cancellation cost by evaluating each passenger itinerary while considering the seat capacity limitations.

Large-scale optimization method

Due to the large number of decision variables and constraints in the integer programming formulation of integrated recovery problems for aircraft and passengers, most publications solve them in several stages.

Some studies obtain aircraft routings in the first stage and then a passenger reassignment solution in the second stage. In Eggenberg et al.^[75], the first stage focuses on the aircraft recovery problem with maintenance scheduling using column generation, and the second stage concentrates on the passenger recovery problem by computing a minimum cost flow problem with a seat capacity alternatively. Jozefowiez et al.^[76] and Zhang et al.^[77] both introduce a three-stage solution method for the integrated recovery problem of aircraft and passengers. In Jozefowiez et al.^[76], the first two stages focus on aircraft recovery and passenger recovery successively, and the third stage attempts to transport more passengers to their destinations by creating and inserting new flight sequences into available aircraft routings. In Zhang et al.^[77], however, the three stages mainly deal with aircraft recovery, flight rescheduling, and passenger recovery successively.

Other studies solve such problems by following a heuristics process; i.e., an initial solution is obtained in the first stage, and an improved optimal solution is derived in the second stage. In the first stage of Mansi et al.^[78], an initial feasible solution is first obtained using mixed-integer programming models and a repairing heuristic. In the second stage, an algorithm is developed based on an oscillation strategy of alternating between constructive and destructive phases to improve the integrated recovery solution. In Sinclair et al.^[79], the initial feasible solution is obtained in the first stage by a large neighborhood search heuristic. The second stage focuses on applying mixed-integer programming for integrated recovery based on a connection network.

Meta-heuristics

The large neighborhood search heuristic is commonly used for airline recovery, especially for aircraft and passenger recovery. Bisaillon et al.^[11] represent the integrated recovery problem of aircraft and passengers with an oval description and then introduce the large neighborhood search heuristic to solve the problem. Sinclair et al.^[80] improve the heuristic introduced in Bisaillon et al.^[11] by adding some steps to the proposed three phases. Then, Sinclair et al.^[79] use the solution result of the large neighborhood search (LNS) heuristic in Sinclair et al.^[80] as the initial variables of the column generation algorithm.

Based on a neighborhood heuristic, Hu et al.^[81] propose the greedy randomized adaptive search procedure (GRASP) heuristic by combining a semi greedy heuristic and the neighborhood search heuristic. Another optimization method based on a multiobjective genetic algorithm was created by Yang & Hu^[82] for a novel integrated recovery problem considering passenger preferences. Zhao et al.^[83] produced a two-stage algorithm compared with a rolling horizon approach. Chen et al.^[84] developed an adaptive non-dominated sorting genetic algorithm-II based on dominant strengths (ANSGA2-DS).

Integrated recovery of all three resources

Due to the complexity of practical irregular operations in the airline industry, there are fewer studies on the fully integrated recovery of aircraft, crews, and passengers. Most papers solve the integrated problem using various methods to limit recovery scopes. For example, Brunner^[85] limits recovery in a terminal airport when a ground delay program (GDP) is issued.
Petersen et al.^[86] and Maher^[87] solve the integrated recovery problem in several stages by column and row generation methods. Arıkan et al.^[88] represent a novel flight network to limit the size of the recovery, which has been commonly used in
Aktürk et al.^[38] and Arıkan et al.^[71]. Few studies use heuristic algorithms like the rolling horizon algorithm^[89], large neighborhood search algorithm^[90], and variable neighborhood searches^[91].

Research findings

(1) Competition has greatly promoted the development of the research field. According to statistical analysis, it was found that most papers (approximately 20 publications of a total of 30 papers) focus on the integrated recovery of aircraft and passengers. The large number of studies is a benefit of the 2009 ROADEF Challenge. Approximately six papers tested their algorithms using instances from the challenge.

(2) In integrated recovery, including passenger reassignment, it is generally assumed that passengers obey the arrangement of airlines and that passengers can only stay in the original itineraries unless passengers cannot arrive at their destinations through the original itineraries. This is somewhat inconsistent with the actual recovery operation for passengers. If their original itineraries are delayed in reality, the passengers have the right to choose their itineraries: endorsing other itineraries or refunding tickets. However, it is difficult to obtain data about passengers' choices under itinerary disruption. We can still make some attempts in the field of operations research. This will promote the development of behavioral operations research in practical airline operations.

(3) Most studies assume that the passenger delay cost is a linear function of delay time, which does not fit reality. Some papers, such as Brunner^[85], Hu et al.^[35], Arıkan et al.^[88], and Santos et al.^[73], think that the passenger delay cost is based on the number of passengers or passenger classes.

(4) Methods that promote passenger recovery have begun to be proposed by combining various traveling modes. Although there are only a few publications, it is a positive attempt.

(5) In terms of the solution algorithm, heuristics have been dominant. Even if the model is directly solved by an optimizer solver, heuristic algorithms are often used. The reasons are twofold. First, due to the large scale of integrated recovery, it is difficult to achieve the required timeliness by relying directly on a commercial optimizer. Second, the goal of disruption management is to pursue the recovery of resources in a short period of time.

Future research directions

Through a qualitative and quantitative analysis of the above topics, the trends of airline disruption management are summarized below. This can provide some direction for future research, especially for new scholars in the field of airline disruption management.

(1) From the perspective of problems, two extremes may occur. One is closer to reality, and the other is related to combinatorial optimization theory.

① Airline disruption management is used to solve practical problems. Some research trends for practical application may occur in the following areas as well as in aircraft recovery problems from single to multiple fleets: i) The disruption period may be unknown and undetermined. ii) Airline disruption management should not only make flight schedules return to the original plan as soon as possible but also use fewer resources, such as swapping aircraft and crews, and consider the environmental effects of aircraft fuel. iii) Airline disruption management is commonly related to multiple agents, such as airlines and passengers. Both of their interests should be considered. iv) Future research may consider more limitations during the recovery process, such as air traffic flow constraints and airport congestion. v) Some recovery measures can also be frequently considered in the near future, such as cruise speed control, combining various traveling modes, and starting the recovery process before a disruption occurs. Although the measures are only involved in a few papers, they are commonly used in airline practical operations.

② Although airline disruption management is an NP-hard problem, under assumptions based on practical operations, some simplified problems can also have good optimal properties in terms of combinatorial optimization. Of course, this is often the task of scholars in the fields of applied mathematics and computation theory. However, anything is possible, especially in the case of interdisciplinary work becoming increasingly common.

(2) The construction of the model tends to become more complex. Combined with the analysis of practical operations of airline disruption management, models can be extended in the following directions.

① As airline disruption management aims at returning to the original plan as soon as possible, it is the goal of the recovery model to be easy to solve and to obtain a solution efficiently. It is still popular to construct an effective and simple model to exactly describe the airline disruption management process. For example, a multistage model can be established according to the peak period of flight operations in hub airports.

② For a problem with an uncertain disruption period, stochastic programming must be developed. This may exceed the research scope of traditional deterministic optimization models for airline disruption.

③ Whether aiming to complete flight recovery as soon as possible using few resources or to balance multiple agents' interests, multiple objectives should be employed. Traditional models of airline disruption management are only concerned about the recovery cost. Even aircraft rerouting must be converted into costs to simplify the model. However, the current trend is to acknowledge the necessity of the diversity of the model objectives. This is closely related to the essence of airline disruption management, i.e., minimizing the negative impacts of disruption for flights, aircraft, crew, passengers, and even hub airports.

④ Airline disruption management is closely related to multiple agents. Aircraft and crews are internal resources of the airline, while passengers are the subject of the airlines' service. Therefore, airline disruption management mainly involves the interests of the airline and passengers. However, airlines are mainly concerned with short-term economic interests, while passengers pay more attention to their psychological feelings under itinerary disruptions. Therefore, studies of passengers' feelings should be added to airline disruption management solution methodologies. A multi-agent approach, which has been proven valid for managing airline disruption management by De Castro^[93] and Bouarfa et al.^[40], could be applied to solve the model.

⑤ Although airline disruption management is concerned with post-disruption recovery, subsequent disruptions may continue to occur. Therefore, the robust optimization of the recovery model should be given more attention. Even the combination of robust planning before the occurrence of disturbance and disruption management after the occurrence of the disturbance should also be considered in the future.

(3) Due to the increasing complexity of the problem and model of current airline disruption management, the efficiency and effectiveness of the solution approach in both computation time and recovery period are important. After all, returning to the original plan as soon as possible is the main goal of airline disruption management.

① Heuristics have to be used more often than before in solving the problem. Multiple objective models and nonlinear models are currently often used to describe airline disruption management. Perhaps some nonlinear solvers can be capable of solving nonlinear models. However, in the short term, researchers have to resort to the combination of heuristic and commercial optimization solvers for solving the practical multiple objective model. Moreover, it is still difficult but important to promote solving multiple objective models and nonlinear models efficiently by using commercial optimization solvers.

② The actual recovery rules can be combined into the airline disruption management solution approach in future research. This will improve the efficiency. For example, changes to the flight peak period in hub airports and cruise speed have been added to the solution methodology design.

③ Machine learning can also be used for airline disruption management in several ways. First, as airline disruption management is commonly solved based on networks and in several stages, the traditional solution approach can be replaced with machine learning, in particular, deep learning based on neural networks and reinforcement learning based on a multistage recovery process. Second, new solution approaches can be generated by combining traditional combinatorial optimization algorithms and machine learning algorithms. For example, in integrated recovery, passengers' behavior and feelings can be analyzed by machine learning and data analysis methods, and then the analysis results can be used in the subsequent recovery process. Additionally, a database of historical disruption scenarios and corresponding recovery solutions can be constructed for current efficient disruption management, where the management of historical scenarios and response to current disruption requires machine learning technology. In the future, we may see some corresponding research achievements.

Conclusions

In this paper, airline disruption management papers from 2010 to the end of July 2024 were reviewed, following Clausen et al.^[8]. The surveyed papers were categorized in several different ways to show the journal distribution in the area, the statistics of different resources of airline recovery, the trends in the number of papers by year and type of resources, and the statistics of disruption scenarios and recovery options, as well as providing a summary of the above statistics. The papers were further categorized based on the types of recovery resources, and for each of these categories, the structure of optimization models, the solution approach and the performance suggested by these papers were provided. This was done by defining their network, types of resources, objectives, solution methodology, case data, and running time (see Tables 1−6). In addition, the research findings for each of these categories were assessed based on a comparison with Clausen et al.^[8]. Finally, the trends in the three areas of problems, models, and solution approaches were highlighted and discussed to provide researchers in the area of airline disruption management with potential future research directions. We believe that following these suggested future research directions will lead to models that are realistic and applicable for use in future airline operations.

Acknowledgments

This research was partially supported by the National Natural Science Foundation of China (71801061), the Philosophy and Social Science Research Planning Project of Heilongjiang Province (23GLB032), the Natural Science Foundation of Heilongjiang Province (LH2021G003), the Fundamental Research Special Funds for the Central Universities-Research and Innovation Fund for Doctoral Students (BK20230904), the Stable Supporting Fund of National Key Laboratory of Underwater Acoustic Technology (JCKYS2023604SSJS021).