-
At present, the research focus of high nitrogen energetic materials at home and abroad is mainly focused on triazole and tetrazole compounds, among which tetrazole compounds are the main ones. This is mainly because tetrazole, as a kind of polyazole heterocyclic compounds, is a structural unit with the highest nitrogen content, which can exist stably except for total nitrogen compounds. The five membered aromatic ring structure can bring additional ring tension to further improve energy. At the same time, the unique large π bond structure of the aromatic ring forms a conjugate system, which not only improves the molecular density, but also greatly enhances the stability of the ring[1,2,3]. The basic structural unit of tetrazole compounds is the tetrazole group, the molecular formula is CHN4, the content of nitrogen element is up to 80%, and the heat of formation is 235.7 kJ·mol–1[1]. It is a typical planar high nitrogen heterocycle structure[4]. Four ring and its derivatives have high density, which can produce a lot of energy when they explode or burn. Consequently, the research on the energy and stability, especially the thermal stability of tetrazole compounds have great significance[2,5].
Researchers from all over the world have synthesized a variety of new tetrazolium compounds in small doses in the laboratory. It is a necessary condition that mastering their thermal hazard properties and decomposition mechanism, so as to provide the prevention and control technology of tetrazolium explosion accidents in production, transportation, storage and apply with theoretical support before putting them into use. Generally speaking, the thermal safety parameters obtained by thermal explosion tests are close to the real situation. However, this method requires a large number of samples, high economic cost and a long period of time[6]. For some newly synthesized materials in the laboratory, this method is difficult to apply. The evaluation of thermal decomposition kinetics to evaluate the quality of thermal safety has become a very important method. The thermal stability and thermal decomposition experiments of materials can be tested by differential scanning calorimetry (DSC), thermogravimetry (TGA), microcalorimetry (C80), adiabatic calorimetry (ARC). In 2005, Fischer et al.[7] studied the thermal decomposition action of 1,5-diamino-4-methyl-1H-tetrazolium nitrate and three other tetrazolium compounds by DSC and TGA, and qualitatively analyzed the products by mass spectrometry and infrared spectroscopy. The kinetic parameters were obtained by Ozawa and Kissinger methods, and the decomposition paths of target tetrazolium compounds were studied. The results of the evaluation of decomposition temperature of the three compounds in the conclusion were showing no difference with the evaluation of activation energy. In 2012, Sinditskii et al.[8] studied the thermal decomposition properties of 3,6-dihydrazino-1,2,4,5-tetrazine (DHT) and 3,6-bis(1-hydrogen-1,2,3,4-tetrazole-5-amino)-1,2,4,5-tetrazine under isothermal and non isothermal conditions. The thermal decomposition kinetic parameters were further solved to explain the pyrolysis mechanism, and combustion experiments are carried out to evaluate the combustion performance. In 2015, Zhu et al.[4] studied the thermal decomposition characteristics of energetic substance N, N'-dinitro-4,4'-azo-Bis (1,2,4-triazolone) (DNZTO) by using TGA and ARC. According to the exothermic curves of DNZTO and ARC tests, the kinetic parameters of DNZTO were estimated. In 2017, Niu et al.[9] studied the thermal stability of dihydroxylammonium 5,5'-bistetrazole-1,1'-diolate (TKX-50) and polymer explosive (PBX) synthesized on the basis of TKX-50 by using DSC, TGA and ARC. On this basis, two kinds of energy materials were calculated and discussed, and significant safety parameters, time under adiabatic conditions to maximum rate and self-accelerating decomposition temperature (SADT) were obtained. Finally, the temperature of thermal explosion of TKX-50 and TKX-50 PBX was further explored according to the influence of safety parameters, storage conditions and environment.
Thermal analysis experiment can only obtain the product types of decomposition of high nitrogen compounds, but the decomposition path and mechanism are difficult to explain clearly only through the macro experimental data. Quantum chemistry can speculate the microstructure of intermediate products, predict the possible decomposition paths of reaction, and speculate the way and mechanism of material decomposition from the micro theoretical level. In 2006, Silva et al.[10] , studied the molecular structure and thermochemical performance of nitrogen-containing five membered heterocycles and their anions and radicals. Multiple theoretical approaches were used to calculate the formation enthalpies of pyrrole, pyrazole, imidazole, 1,2,3-triazole, 1,2,4-triazole, 1H tetrazole and 2H tetrazole, and the relationship between the number of nitrogen atoms in heterocycles and their enthalpies was established. In 2013, Wu et al.[11], researched the formation heat, electronic structure, energy performance and thermal stability of different substituents of nitroso benzotetrazole derivatives by applying DFT-B3LYP method, and the heat of formation of all substituted compounds is higher than that of their parent compounds. As the content of nitrogen atoms in the nitrobenzene ring adds up, the heat of formation of derivatives with the same substituents increases by degrees. The lowest unsubstituted orbital of most substituted compounds was higher than that of corresponding unsubstituted compounds, and the detonation performance was improved also. In 2016, Zhao et al.[12], studied the pyrolysis mechanism of six tetrazole derivatives by experiments, estimated the electrostatic potential of several tetrazole compounds by DFT method, established the electron cloud distribution of molecules, and judged their stability. The results show that the ring opening of tetrazolium occurs after the melting of nitrogen heterocyclic compounds, and the decomposition of nitrogen is the main decomposition path.
In conclusion, in this paper, high-pressure differential scanning calorimeter (HPDSC) was used in the low-dose dynamic thermal decomposition experiment of (5-(4-pyridyl) tetrazolate), to obtain the thermal safety parameters, and Gaussian 16 software was used to obtain the primary decomposition path of 4-pyridyltrazole. The activation energy calculated in the experiments was compared with that calculated by DFT theory.
-
The sample of H4-PTZ was purchased from Changshu Institute of Technology (China), with purity of more than 90%.
Experimental conditions
-
The differential scanning calorimetry adopts Mettler DSC HP1 calorimeter. Test conditions are as follows, sample volume is 2.0 ± 0.1 mg; heating rate are 2.0, 5.0, 8.0, 10.0, 15.0 K·min–1 respectively; detection sensitivity is 0.04 mw; temperature range is 50–320 °C (323.15–593.15 k); dynamic nitrogen atmosphere; flow rate is 20 ml·min–1.
-
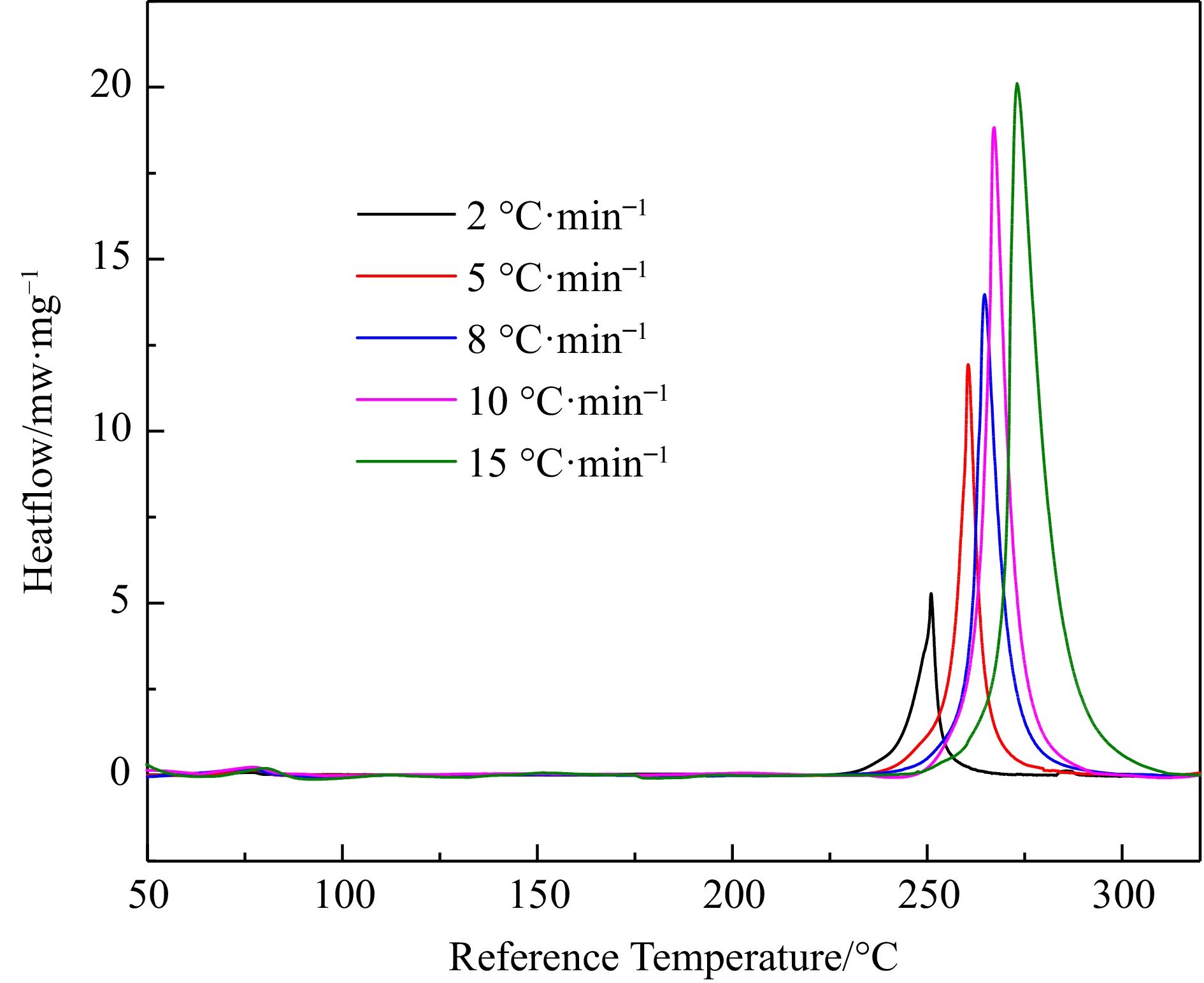
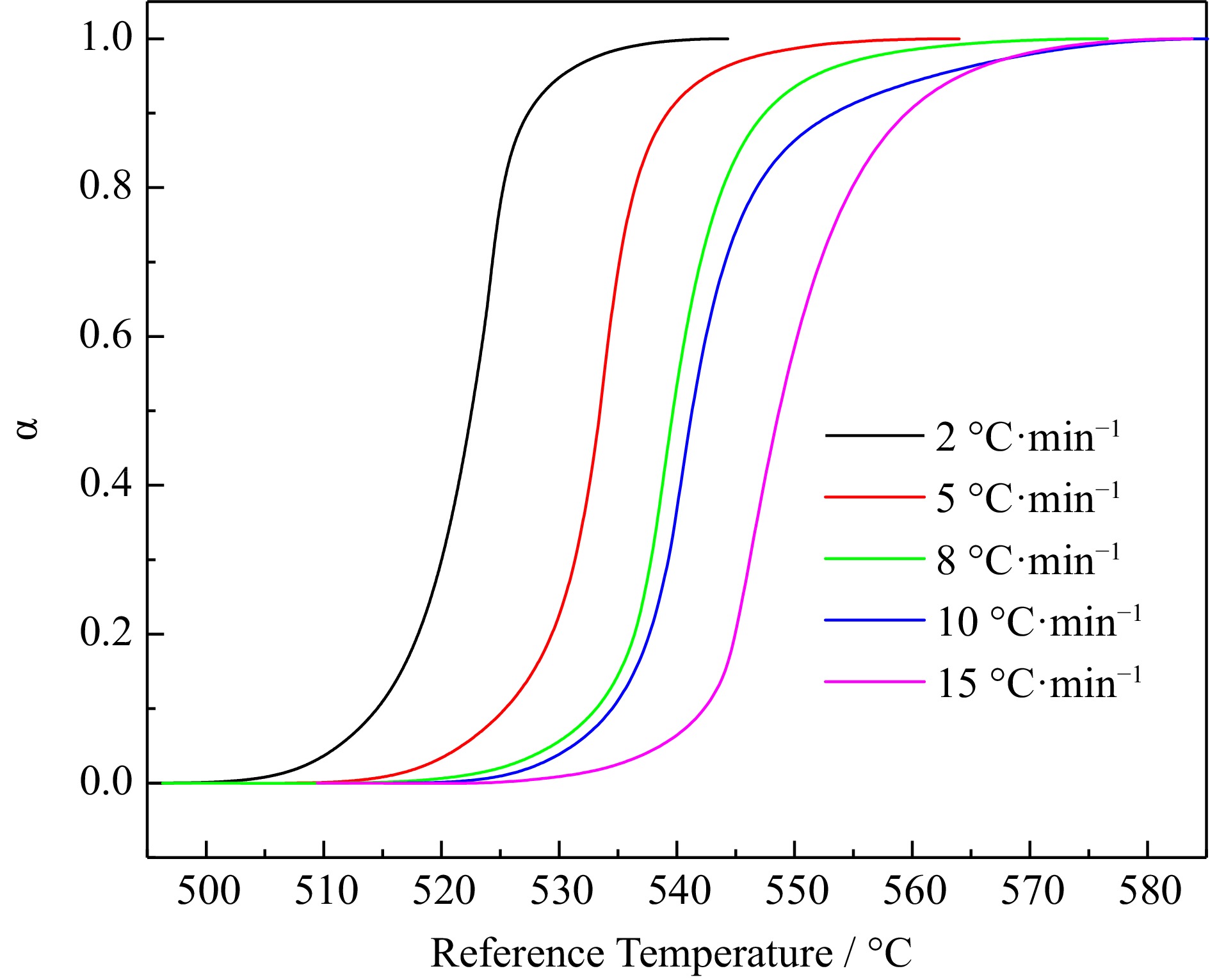
The heat flow change curve and reaction process change curve of H4-PTZ thermal decomposition process are shown in Fig. 1 and Fig. 2.
See Table 1 for the characteristic parameters of thermal analysis under different heating rates. There is an obvious exothermic peak between 225−325 °C in Fig.1, indicating that H4-PTZ decomposes in this temperature range. With the increase of β, the initial decomposition temperature T0 moves backward, the maximum reaction rate temperature TP increases, and the heat output also increases, indicating that the increase of temperature rise rate intensifies the decomposition of H4-PTZ. In addition, the tangent slope of the exothermic peak curve in Fig. 1 is relatively large, which indicates that once H4-PTZ decomposition reaction is triggered, it will soon reach the maximum decomposition rate, which is not conducive to accident prevention and control. At the same time, the decomposition process of the reactant is fast, and the reactant can be completely transformed in a short time. Figure 2 shows that the conversion rate changes in 'S' shape with temperature, and moves to the right with the increase of β.
Table 1. Thermal decomposition parameters at different heating rates for H4-PTZ.
Β (°C·min–1) T0 (°C) Tp (°C) Tend (°C) ΔHd (J/g) 2 249.03 251.3 253.3 1147.33 5 258.19 261.45 264.7 1055.02 8 262.71 267.38 272.88 924.26 10 264.03 268.78 273.58 1084.23 15 270.07 275.37 284.96 929.36 Dynamic calculation
-
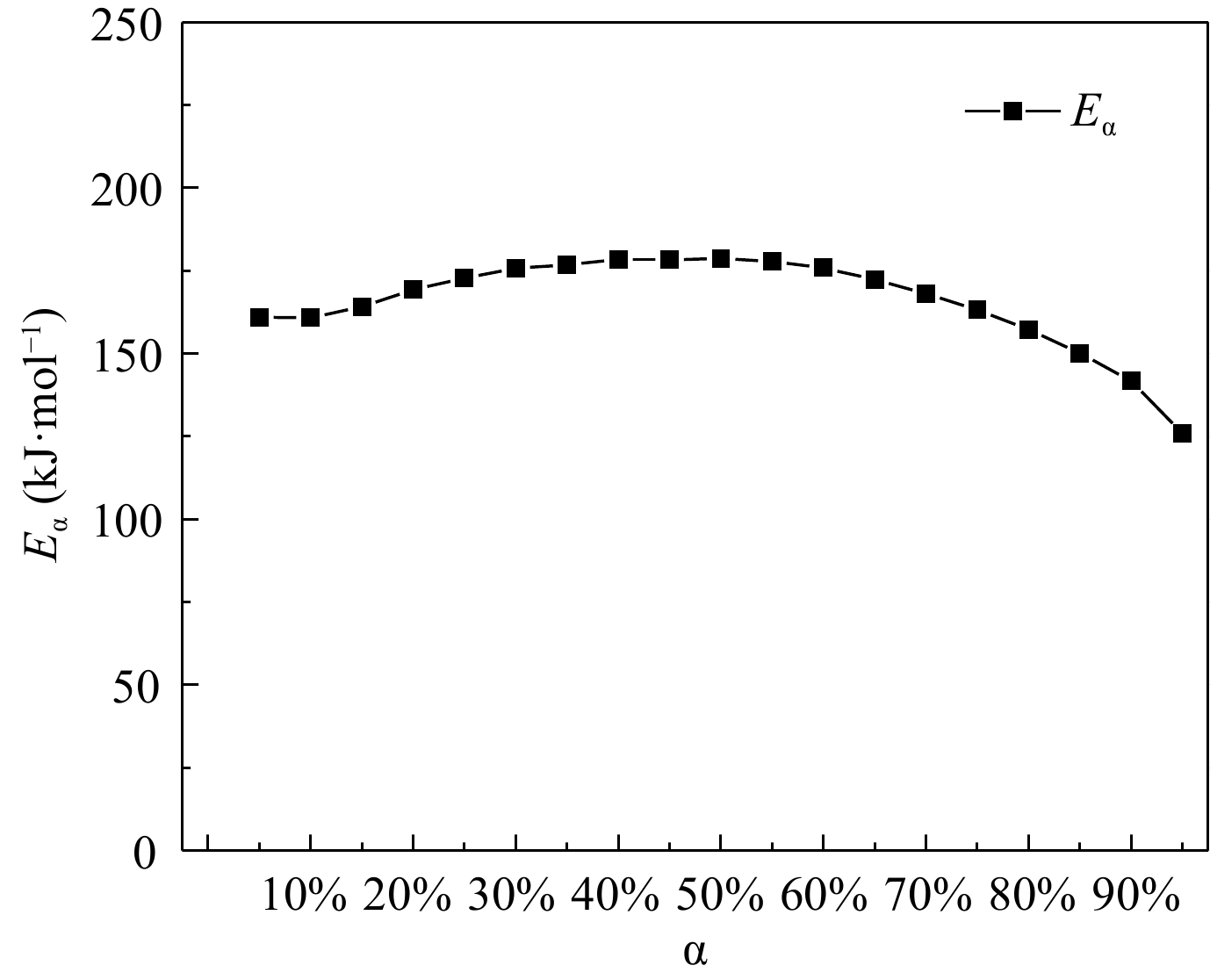
The equal conversion method can calculate the activation energy directly without involving the kinetic model function, and the value obtained is more reliable than the traditional kinetic method. This paper calculated the activation energy value in the range of 5%−95% by starink equal conversion method, and the change trend of conversion rate in the whole reaction process was obtained. The starink fitting equation is shown below[13]:
$ {ln}\left(\frac{\beta }{{T}^{1.92}}\right) = -1.0008\frac{{E}_{\alpha }}{RT} + constant $ (1) Fitting the value of
$ \mathrm{ln}\left(\frac{\mathrm{\beta }}{{{T}}^{1.92}}\right) $ The crest value temperature corresponding to the maximum reaction rate was substituted into Kissinger[14] and Ozawa[15] equations, and the activation energy was calculated by fitting the data at the crest value temperature. See Table 2 for the fitting results.
Table 2. Apparent activation energy using different methods.
Kissinger Ozawa Eα (kJ·mol–1) lnA (s–1) Eα (kJ·mol–1) Tp 194.35 42.82 193.29 T0 – – 220.07 -
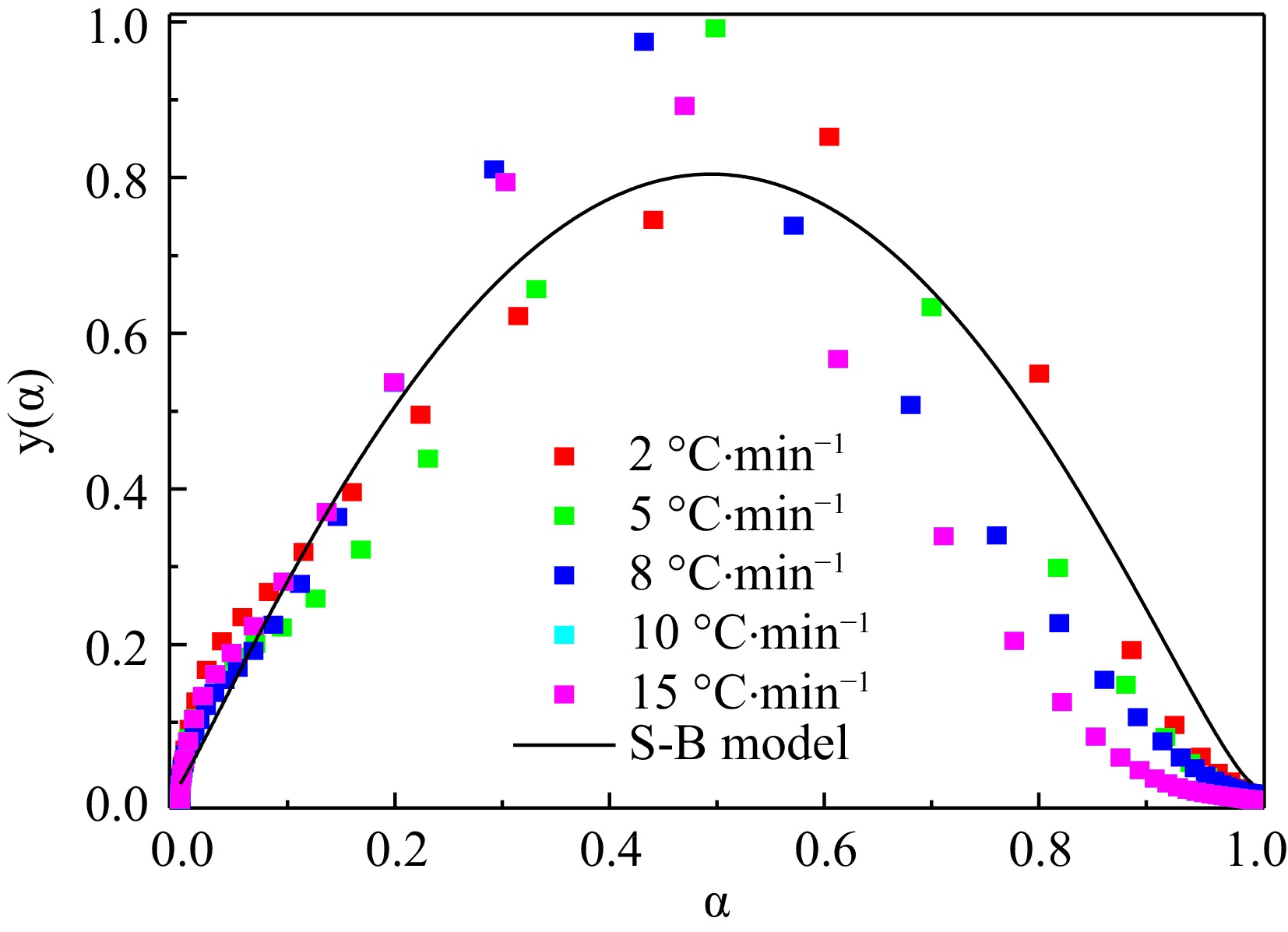
There are many methods to determine the reaction mechanism function, but most of them have errors caused by the assumption and approximation of the mechanism function form. The Malek method narrowed the range of dynamic mechanism function obviously, and there are almost no assumptions and approximate conditions in this method. Therefore, it improves the accuracy of the study of mechanism function form. According to Malek, the self defined function y(α) is introduced, which can be used for fitting to judge the mechanism function type. y(α) can be calculated by formula (2)[16].
$ y(\alpha ) = {(\frac{{d\alpha }}{{dt}})_\alpha }\exp (\frac{{{E_0}}}{{R{T_\alpha }}}) = {\text{Aexp}}( - \frac{{{E_0}}}{{R{T_\alpha }}})f(\alpha ){\text{exp}}( - \frac{{{E_0}}}{{R{T_\alpha }}}) = Af(\alpha ) $ (2) The y(α) was normalized to [0,1], and then the nonlinear fitting was performed to compare the shape with the standard function curve. Table 3 is several common forms of mechanism function f(α)[17].
Table 3. Several common forms of f(α).
No. Expression of f(α) No. Expression of f(α) 1 αm 6 (1–α)n[–ln(1–α)]p 2 (1–α)n 7 (1–α)m[1–(1–α)n]p 3 [–ln(1–α)]p 8 (1–α)m[(1–α)n–1]p 4 αm(1–α)n 9 n(1–α)[–ln(1–α)]1–1/n 5 αm[–ln(1–α)]p 10 (1–α)n(1+kα) By fitting the relationship between α and f(α) at different temperature rising rates in five groups, the thermal decomposition reaction mechanism is the solid-phase decomposition reaction mechanism, which conforms to the mechanism function No.6, f(α) = (1–α)2.09[–ln(1–α)]1.24. The total fitted image is shown in Fig. 5.
-
The thermal safety parameters of energy-containing materials mainly include: TSADT, TTIT and Tb, which are important to the use of energetic materials. The calculation methods of TSADT, TTIT and Tb are shown in Eq. (3)–(5). The calculation results are shown in Table 4[18].
Table 4. Thermal safety evaluation parameters.
Eoe
(kJ·mol−1)Eop
(kJ·mol−1)Te0
(°C)Tp0
(°C)TSADT
(°C)TTIT
(°C)Tb
(°C)5-(4-Pyridyl)tetrazolate 220.07 193.29 244.15 245.32 244.15 254.68 257.43 $ T_{0\;{\rm{ or}}\;{\rm p}} = T_{{\rm e}0\;{\rm{ or}}\;{\rm{ p0}}} + a\beta_{i} + b\beta_{i}^{2}, \;\;(i = 1-5) $ (3) $ SADT = T_{\rm{e0}} $ (4) $ T_{\rm{TTT}\;{\rm{or}}\;{\rm b}}=\frac{E_{{\rm o}\;{\rm{or}}\;{\rm p}}-{\sqrt {E_{\rm o}\;{\rm{or}}\;{\rm p}^2-4E_{{\rm o}\;{\rm {or}}\;{\rm p}}RT_{{\rm {e0}}\;{\rm{or}}\;{\rm {p0}}}}}}{2R} $ (5) In addition to the thermal safety parameters of energetic materials, the thermodynamic parameters are also significant properties of energetic materials. Common thermodynamic parameters are: ΔH, ΔS, ΔG. They can be calculated by Eq. (6)–(8). The calculation results are shown in Table 5.
Table 5. Thermodynamic parameters.
ΔS≠ (J·mol−1·K−1) ΔH≠ (kJ·mol−1) ΔG≠ (kJ·mol−1) 5-(4-Pyridyl)tetrazolate 106.52 194.35 139.13 $ A=\frac{K_{\rm B}T}{h}\exp\left(\frac{\Delta S^{ \ne}}{R}\right) $ (6) $A\exp\left(-\frac{E}{RT}\right)=\frac{k_{\rm B}T}{h}\exp\left(\frac{\Delta S^{ \ne}}{R}\right)\exp\left(-\frac{\Delta H^{ \ne}}{RT}\right)$ (7) $ \Delta G^{ \ne}=\Delta H^{\ne}-T\Delta S^{\ne}$ (8) $ T = T_{{\rm p}0},\;\; E = E_{\rm k},\;\; A = A_{\rm k}. $ -
The method used in this paper is mainly carried out by Gaussian View 6.0.16 and Gaussian 16 program. The calculation accuracy and convergence standard are set by the program. B2PLYP/def2-TZVPP//B3LYP/6-311+G(d, p)[19] composite group was used to discuss the decomposition mechanism of H4-PTZ.
Geometry optimization
-
H4-ptz is optimized at the calculation level of B3LYP/6-311+G(d, p). The results are shown in Fig. 6, and frequency analysis is conducted using the same method. The results are all positive, indicating that the corresponding optimized configuration is a stable geometric configuration. Furthermore, H4-PTZ potential surface is scanned flexibly, and it is showed that the optimized configuration corresponds to the minimum energy point on the surface of potential energy, which verifies the stability of the optimized configuration.
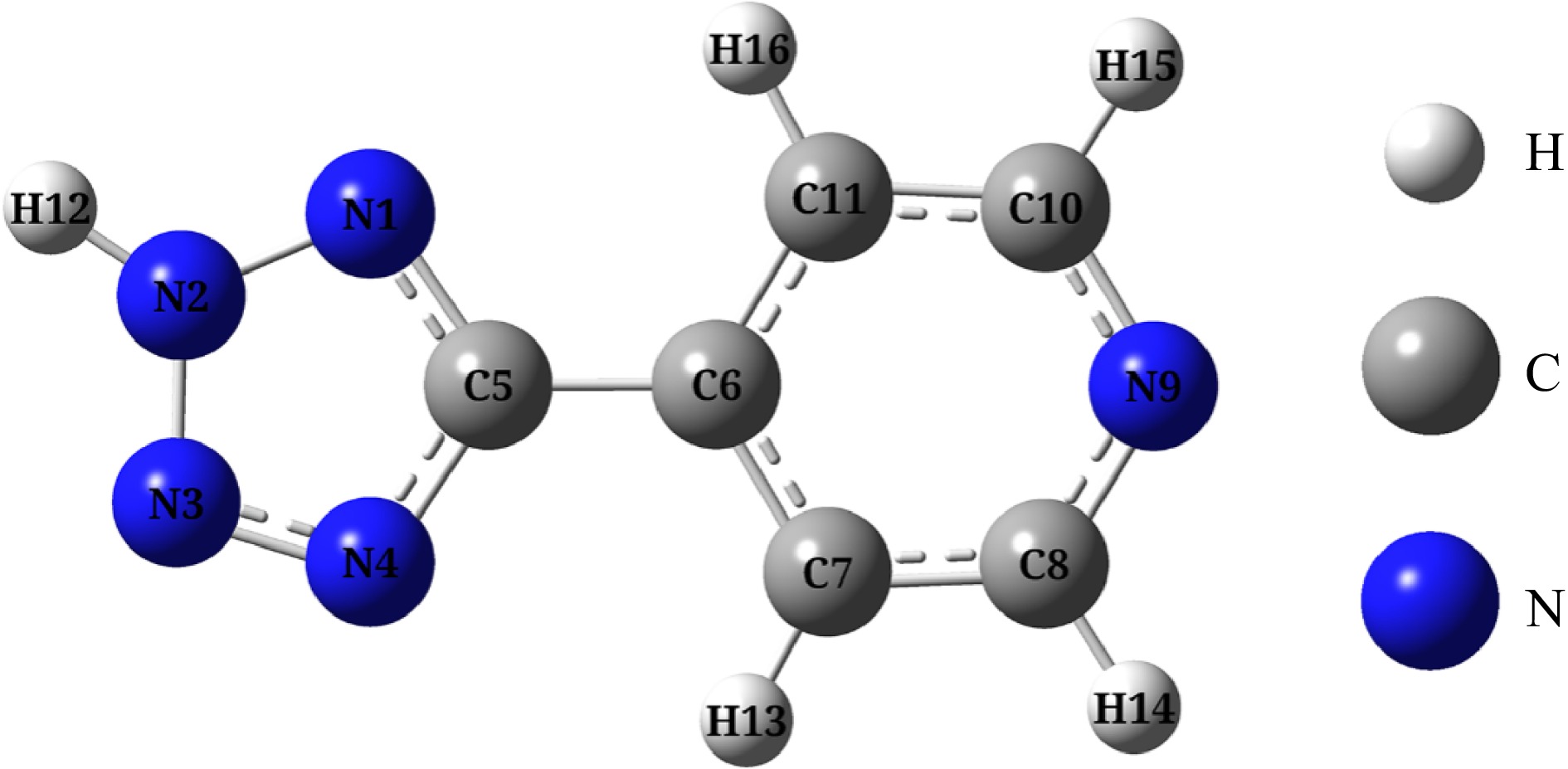
Figure 6.
Optimized configuration of H4-PTZ (Note: The atomic number in the molecule has been labeled, and there are the same number of atoms).
Mulliken charge
-
Mulliken charge can directly show the local charge distribution of molecules, which is directly related to the chemical bond in molecules, and affects the dipole moment, electronic structure and other important properties. Mulliken charge distribution of H4-PTZ is obtained at B3LYP/6-311G(d, p) calculation level. The results are shown in Table 6. The conclusion is the net charge of all atoms in the molecular structure of H4-PTZ is zero, that is, the molecule is neutral. The charge of tetrazole ring is –0.254e, the charge range of N atom on the ring is –0.266e ~ –0.01e, and N4 has the most negative charge, which indicates that H bond should be connected with N4, but in the actual structure, H bond is connected with N2, which indicates that the steric effect is more dominant than the electronic effect.
Table 6. Mulliken atomic charges of H4-PTZ at B3LYP/6-311G(d, p) level(e).
Atom Charge Atom Charge N1 −0.219 N9 −0.285 N2 −0.111 C10 +0.071 N3 −0.010 C11 −0.123 N4 −0.266 H12 +0.260 C5 +0.352 H13 +0.117 C6 −0.070 H14 +0.115 C7 −0.122 H15 +0.113 C8 +0.071 H16 +0.108 Surface electrostatic potential
-
Electrostatic potential (ESP) plays a key role in describing the electrostatic interaction between molecules. At the calculation level of B3LYP/6-311+G(d, p), the surface electrostatic potential distribution of H4-PTZ is obtained by combining the evaluation of multiwfn and VMD (visual molecular dynamics). Figure 7 shows that the positive electrostatic potential is mainly distributed near the H atom and N2 atom on the tetrazole ring, while the negative electrostatic potential is most distributed around the N atom of the pyridine ring and the N3 and N4 atoms of the tetrazole ring. The area proportion and strength of positive electrostatic potential are larger than that of negative electrostatic potential, which is according to the electrostatic potential distribution law of energetic materials proposed by Klapötke and other scholars[20].
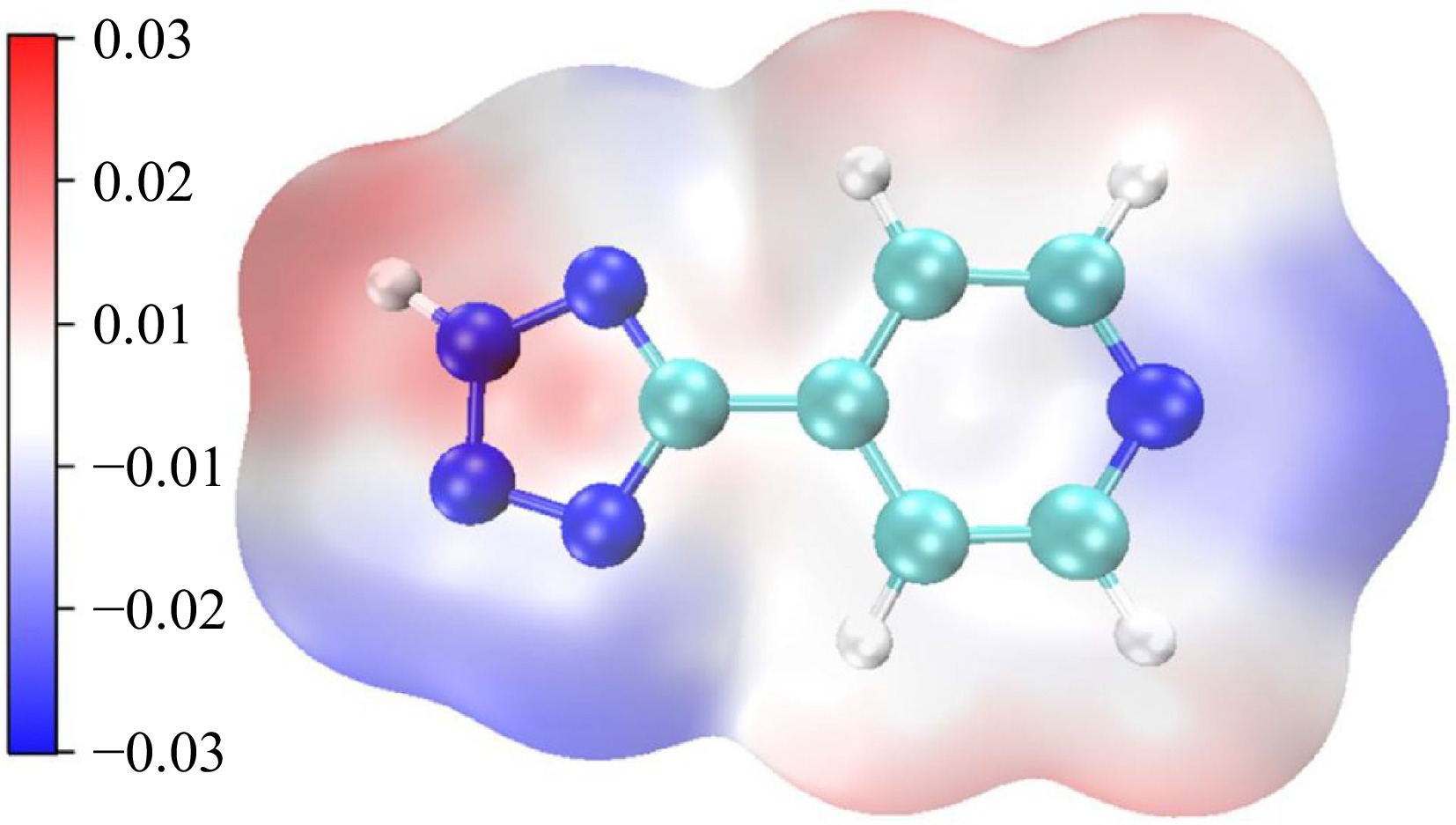
Figure 7.
Potential electrostatic distribution of H4-PTZ (Note: Blue represents a positive electrostatic potential and red represents a negative electrostatic potential).
Decomposition path
-
According to the molecular structure of H4-PTZ and the possible pathway of nitrogen generation, four possible decomposition pathways including proton transfer pathway were explored. In the molecular structure, there is a double bond structure between N3-N4 and N1-C5, which is not easy to break. The tetrazole ring is closely connected with the pyridine six membered ring, and it is also not easy to break. Therefore, when exploring the thermal decomposition reaction process, first consider the ring opening reaction acting on the N1-N2, N2-N3 and N4-C5 bonds. The comprehensive design of the decomposition mechanism is shown in Fig. 8a, and the red line is broken key position.
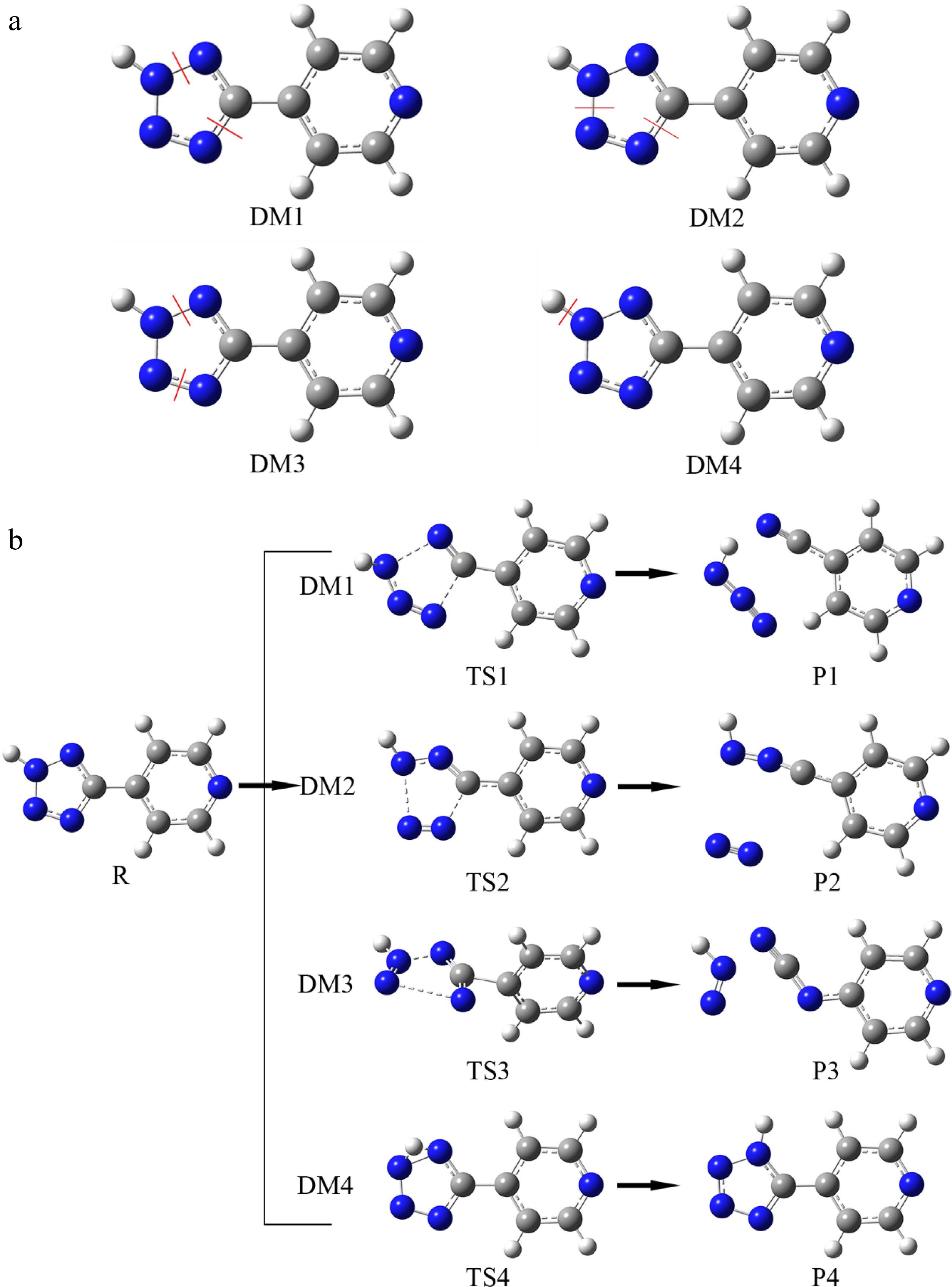
Figure 8.
The reasonable initiation reactions and corresponding decomposition pathways of H4-PTZ. (a) Representing four superficially reasonable initiation reactions; (b) corresponding ecomposition pathways.
(1) N1-N2 and N4-C5 bonds break at the same time (DM1); (2) N2-N3 and N4-C5 bonds break at the same time (DM2); (3) N1-N2 and N3-N4 bonds break at the same time (DM3); (4) due to the relatively active H12 on the tetrazole ring, the thermal decomposition reaction may also be carried out by the proton transfer of H12 (DM4).
Structural optimization and verification of reaction transition state
-
Through the four possible decomposition reaction pathways described, the transition state is searched with the optimized configuration of H4-PTZ, and the reactants and products connected with the transition state are confirmed by IRC analysis. See Fig. 8b for the corresponding decomposition reaction pathway. According to the frequency analysis of the reactant and each standing point in different decomposition paths, it is found that the transition state has a corresponding unique negative virtual frequency value (Table 7), and there is no virtual frequency in the reactant and the product. Figure 9 shows the optimized configuration and main bond length values of the transition state and the corresponding product. The detailed calculation and analysis results of each decomposition path are as follows.
Table 7. Negative imaginary frequencies of transition states at B3LYP/6-311+G(d, p) level (cm−1).
TS TS1 TS2 TS3 TS4 Frequencies 517.64i 438.40i 450.68i 1744.57i 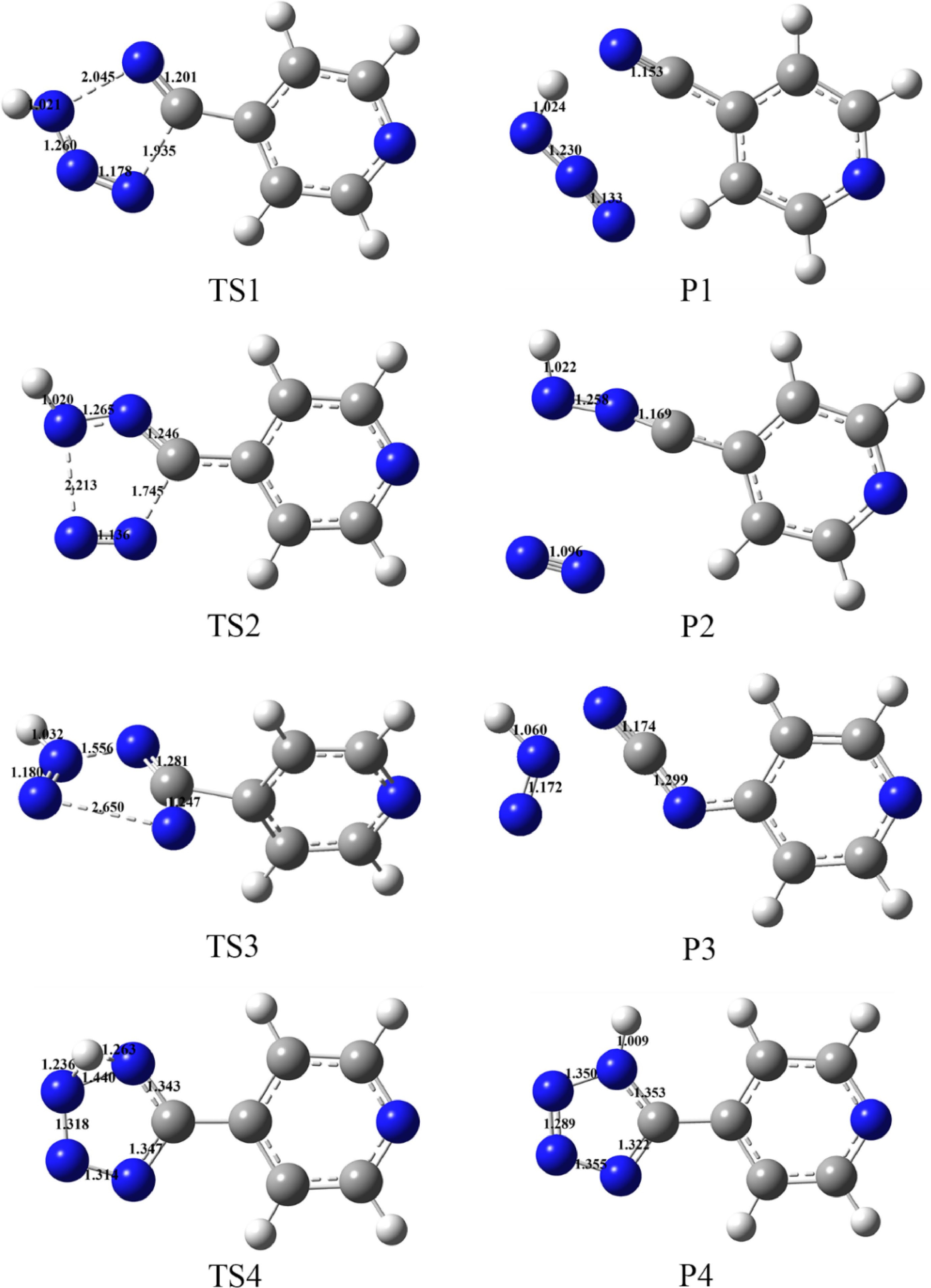
Figure 9.
Optimized configuration and bond lengths (Å) of transition states and products at B3LYP/6-311+G(d, p) level.
In route DM1, TS1 was found by lengthening N1-N2 and N4-C5 bonds on tetrazole ring and verified by IRC. In this process, N1-N2 and N4-C5 bonds broke at the same time and then separated from HN3 unit. At TS1, the distance between N1 and N2 atoms increases to 2.045 Å, and the distance between N4 and N5 atoms increases to 1.935 Å. At this time, the bond angle N1-C5-C6 is 140.151°, H12-N2-N3 is 144°, and N2-N3-N4 is 133.567°. The dihedral angles of H12-N2-N3-N4 and C11-C6-N1-N2 are −135.261° and −15.236° respectively, indicating that the atoms on the tetrazole ring are not in the same plane, and the HN3 unit in the product is in plane configuration, containing conjugated π bond to make the molecule stable.
In route DM2, The bond length of N2-N3 and N4-C5 increased to 2.213 Å, N4-N5 increased to 1.745 Å, and N3-N4 changed from 1.302 Å to 1.135 Å. After the tetrazole ring was opened, its spatial relative position also changed. The dihedral angle of C5-N1-N2-H12 was 155.507°, C6-C5-N1-N2 was 162.248°, and C11-C6-C5-N1 was 13.344°. Finally, the N-N bond length of N2 unit is 1.096 Å, which is 0.039 Å longer than that of reactant. In the open-loop structure, C6, C5, N1 and N2 atoms are almost in the same straight line, and the bond angle C6-C5-N1 is 179.525°, C5-N1-N2 is 171.631°.
DM3 releases the free radical N2H by elongating the N1-N2 and N3-N4 bonds on the tetrazole ring. In TS3 structure, pyridine ring and tetrazole ring are no longer coplanar, dihedral angle of C11-C6-C5-N1 changes from −0.00993° to 80.615°. With the ring opening reaction of tetrazole ring, the bond length of N1-N2 and N3-N4 increases to 1.556 Å and 2.650 Å, respectively, while C5-C6 bond is also elongated. In the product configuration, the C5-C6 bond breaks, resulting in a new N4-C6 bond. The bond length is 1.368 μm, and the bond angle N4-C5-N1 increases to 174.906°, indicating that the three atoms are almost in the same line and coplanar with pyridine ring. The bond length of N-N bond and N-H bond of the optimized configuration of free radical N2H is 1.172 Å and 1.060 Å, respectively, which is slightly different from that of TS3.
It is found that the bending vibration of H12 will lead to proton transfer and isomerization of H4-PTZ to produce 5-(4-pyridyl)-1H-tetrazole. In the TS4 structure, H12 is located above the plane of tetrazolium ring, and the dihedral angle H12 double bond position changes from N1-C5 and N3-N4 double bond to N2-N3 and N4-C5 double bond. The bond length of N1-H12 in the optimized configuration of isomerization product is 1.009 Å, which is only 0.002 Å different from that of H4-PTZ. The dihedral angle of C11-C6-C5-N1 is −12.385°, indicating that the spatial structure of its tetrazole ring and pyridine ring is not coplanar.
Calculation of thermal decomposition reaction energy
-
At the level of quantitative calculation of B2PLYP/def2-TZVPP, the change of energy in the four main thermal decomposition reaction paths of H4-PTZ is calculated while considering the zero point energy correction. The default reaction temperature is 298.15 K, and the pressure is 1.00 atm. The energy values of H4- PTZ and each stagnation point are displayed in Table 8 below.
Table 8. Energy values of H4-PTZ and each stagnation points (Hartree).
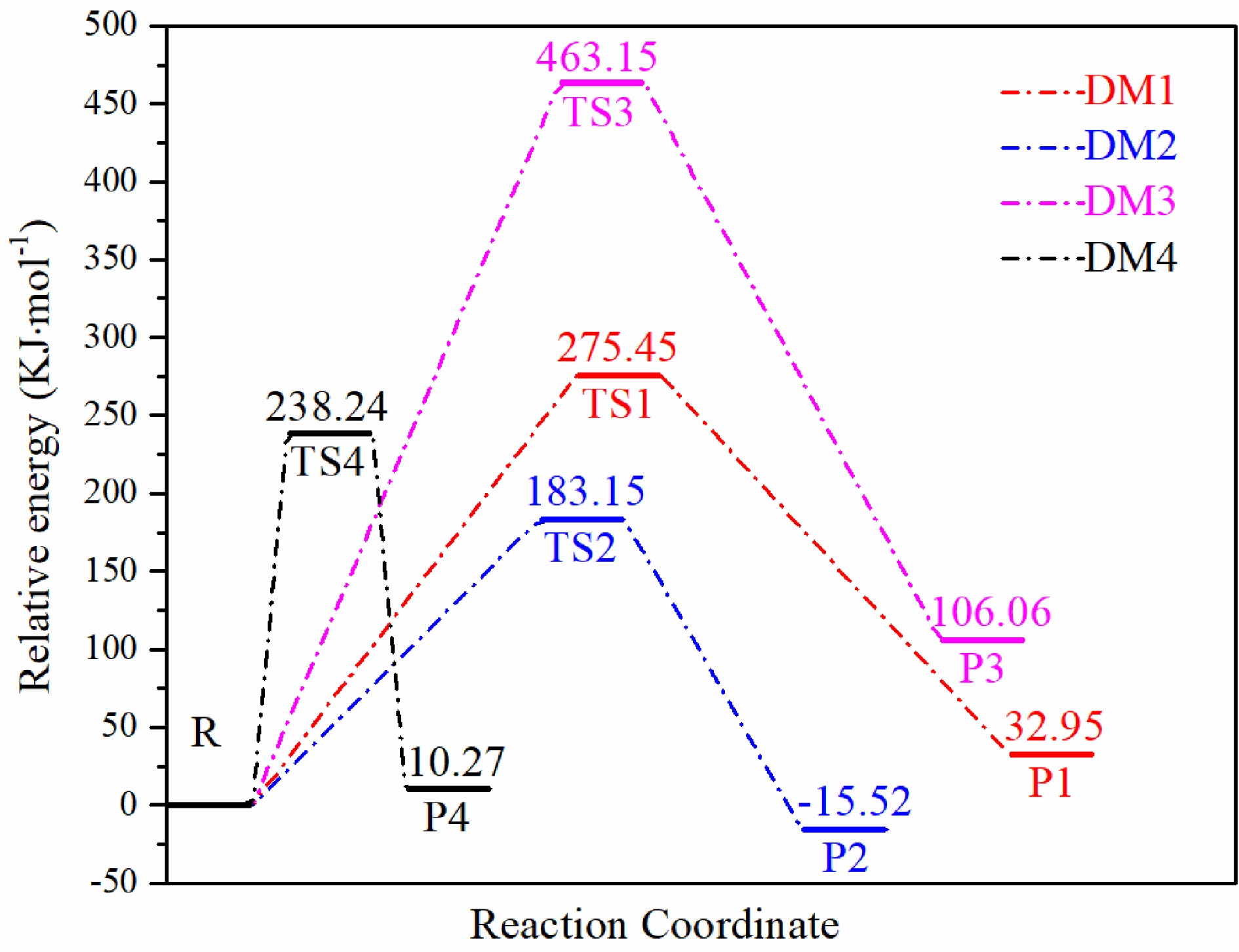
E/B2PLYP ZPE/B3LYP Etot R −504.529662 0.082568 −504.447094 TS1 −504.417169 0.074990 −504.342179 TS2 −504.452378 0.075044 −504.377334 TS3 −504.344675 0.073984 −504.270691 TS4 −504.432017 0.075664 −504.356353 P1 −504.489591 0.055047 −504.434544 P2 −504.507572 0.054567 −504.453005 P3 −504.455678 0.048981 −504.406697 P4 −504.524742 0.081559 −504.443183 According to the calculation method of reaction activation energy, the activation energy values and energy barriers of four main decomposition reaction pathways are obtained based on the energy values of reactants. It can be seen from Fig. 10 that the activation energy to be overcome for the decomposition of DM1 and DM2 is different, 275.45 kJ·mol–1 and 183.15 kJ·mol–1. The activation energy to be overcome in the first step of DM1 is 92.30 kJ·mol–1 higher, which shows that the intensity of N1-N2 bond on tetrazole ring is higher than that of N2-N3 bond, and the difficulty of breaking bond is relatively higher. In the second step, a large amount of energy was released. The activation energy of HN3 unit process released by TS1 in transition state was 242.50 kJ·mol–1, and that of N2 unit process released by TS2 was 198.67 kJ·mol–1. The energy value of P2 was lower than that of reactant, and the difference was 15.52 kJ·mol–1, indicating that P2 was more steady than reactant. In DM3, due to the large rotation between the pyridine ring and the tetrazole ring of TS3, the structural stability of DM3 is reduced, so the activation energy needed to overcome in this pathway is the highest (463.15 kJ·mol–1), and the product P3 is 106.06 kJ·mol–1 higher than the reactant, which is difficult to develop compared with other pathways. In the proton transfer reaction of H12, the first step needs to overcome the activation energy value of 238.24 kJ·mol–1, which is 55.09 kJ·mol–1 different from DM2, and the product P4 is more unstable than the reactant, which indicates that the isomerization reaction is difficult to occur, and does not account for the main part in the thermal decomposition reaction of H4-ptz, so the decomposition path of denitrification after isomerization is no longer taken as the follow-up research content.
In conclusion, DM2 is the main thermal decomposition reaction pathway of H4-PTZ, and its activation energy to overcome is the lowest (183.15 kJ·mol–1), indicating that the ring opening reaction is the first step of the decomposition pathway, and the release of N2 is the critical factor to determine the decomposition reaction.
Contrast of activation energy
-
The activation energy calculated by Kissinger & Ozawa method is 194.35 and 193.29 kJ·mol−1 respectively, which is beside the activation energy corresponding to the reaction pathway of DM2. It shows that the main exothermic reaction in the whole decomposition process of pyridyl tetrazole is the primary ring opening reaction.
-
The initial exothermic temperature of H4-PTZ are 249.03, 258.19, 262.71, 264.03, 270.07 °C, respectively. The decomposition heat is about 1,000 J·g–1.
By adopting the Kissinger approach, the apparent activation energy of H4-PTZ was 194.35 kJ·mol–1. The apparent activation energy of H4-PTZ obtained by the Ozawa method is 193.29 kJ/mol, and starink approach was applied to research the apparent activation energy of H4-PTZ; the range of apparent activation energy of H4-PTZ was 125.86−178.69 kJ·mol–1. The most probable mechanism function of pyridyl trazole is obtained as f(α) = (1−α)2.09[−ln(1−α)]1.24 by using the defined function image and the corresponding eigenvalue data by the Malek method.
Through theoretical calculation, the activation entropy (ΔS), activation enthalpy (ΔH) and activation Gibbs free energy (ΔG) of pyridyl tetrazole are 106.52 J·mol−1·K−1, 194.35 kJ·mol−1, 139.13 kJ·mol−1, respectively. Thermal safety characteristic temperature: TSADT, TB and TTIT are 244.15, 257.43 and 254.68 °C, respectively.
Two kinds of tetrazole compounds were studied theoretically by using Gaussian16 program. This paper uses the B3LYP/6-311G+(d, p) group method in DFT to optimize the initial configuration of H4-PTZ, and the frequency is analyzed at the same level of calculation. The parameters are got such as bond length and bond angle electron energy. On the basis of the optimized configuration, the initial guess of transition state is carried out, and the calculation of internal reaction coordinate (IRC) is carried out. The transition state is taken as the initial scanning structure, and the minimum energy value is gradually searched to both sides, so as to determine the products, intermediates or reactants connected with the transition state. It is confirmed that DM2 is the main thermal decomposition route of H4-PTZ.
Finally, by comparing the activation energy obtained by experimental calculation with that obtained by theoretical calculation, it is found that the reaction of opening the ring of pyridine tetrazolium to release nitrogen is the main reaction of the whole decomposition and exothermic process.
-
The authors declare that they have no conflict of interest.
- Copyright: © 2022 by the author(s). Published by Maximum Academic Press on behalf of Nanjing Tech University. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
-
About this article
Cite this article
Ding X, Zhao S, Ni L, Pan Y. 2022. Thermal hazard and mechanism study of 5-(4-Pyridyl)tetrazolate (H4-PTZ). Emergency Management Science and Technology 2:13 doi: 10.48130/EMST-2022-0013
Thermal hazard and mechanism study of 5-(4-Pyridyl)tetrazolate (H4-PTZ)
- Received: 31 October 2022
- Accepted: 08 December 2022
- Published online: 19 December 2022
Abstract: Thermal decomposition experiment of 5-(4-Pyridyl)tetrazolate (H4-PTZ) was carried out. The heat flow curve and reaction rate data under different heating rates were obtained. The characteristic parameters were obtained. The apparent activation energy for each individual reaction was calculated by applying different methods. On this basis, the Malek method was used to predict the most probable mechanism function of thermal decomposition reaction of H4-PTZ. The thermal safety parameters, including self-accelerating decomposition temperature, hot spot fire temperature and thermal explosion critical temperature were also predicted. The activation enthalpy, activation entropy, and activation Gibbs free energy of H4-PTZ are calculated. Gaussian16 program was used to optimize the molecular structure, search the transition state and calculate the intrinsic reaction coordinates of H4-PTZ. The most probable decomposition path of H4-PTZ was found, and the activation energy calculated by experiment was compared with that calculated by the theory.
-
Key words:
- Tetrazolate /
- Thermal decomposition /
- Thermal safety parameters /
- Decomposition path