An LCC-LCC compensated WPT system with inherent CC-CV transition function for battery charging applications

Introduction

Compared with traditional wired charging, WPT technology has the advantages of safety, aesthetics, and flexibility^[1]. This promising technology has been applied in various industrial fields^[2,3]. Li-ion batteries are extensively employed in the above fields due to their advantages of environmental friendliness, high power density and long lifespan. Lithium batteries are lightweight and environmentally friendly, they are often used by some electrical equipment to store electrical energy. The charging sequence of first constant current (CC) charging and then constant voltage (CV) charging is the charging method that best suits the charging characteristics of lithium batteries. The existing traditional methods that enable WPT systems to achieve stable CC and CV output and their related defects are as follows:

The three closed-loop control methods of phase shift control^[4,5], frequency conversion control^[6,7] and DC-DC converter control^[8,9] are currently commonly used technologies to realize CC and CV outputs. However, all three methods have disadvantages. Phase shift control is difficult to achieve zero-voltage switching and approximate zero-phase-angle (ZPA) operation when the load changes greatly, resulting in increased inverter loss. Frequency conversion control technology has the possibility of frequency bifurcation, which will seriously affect the stability of the system. At the same time, this technology is also difficult to achieve ZPA operation, which will cause reactive power circulation in the system and increase losses. DC-DC converter control technology has a large number of components, high cost, and high system complexity.

The hybrid topology switching method realizes the conversion of the system's CC and CV outputs by controlling the on-off of the switches^[10−13]. However, it introduces additional AC switches, corresponding drive circuits, and passive components in the system, which increases the complexity of the circuit structure.

The dual-frequency switching method is also a commonly used method to realize CC and CV outputs^[14−18]. However, this method is not only difficult to design the parameters of the compensation components, but also difficult to limit the CC and CV frequencies within the frequency range specified by the standard.

To optimize the existing CC and CV WPT systems, this paper proposes an LCC-LCC compensated WPT system, which can not only realize CC and CV outputs but also automatically complete the transition from CC to CV mode. Compared with the previous closed-loop control, hybrid topology switching, and dual-frequency switching methods, the proposed method does not require communication links, state-of-charge detection circuits, and open-circuit protection circuits. Meanwhile, the system works at a fixed frequency throughout the entire working process to ensure system stability. In addition, the system can achieve ZPA operation in CC mode and CV mode, improving the efficiency of the system. Therefore, simple structure high reliability, and low cost can be ensured in the proposed system. It is worth noting that, similar to the above-mentioned hybrid topology switching method and dual-frequency switching method, the proposed method is suitable for scenarios with fixed mutual inductance, such as electric bicycle charging applications.

Theoretical analysis

Overview of the proposed LCC-LCC Compensated WPT system

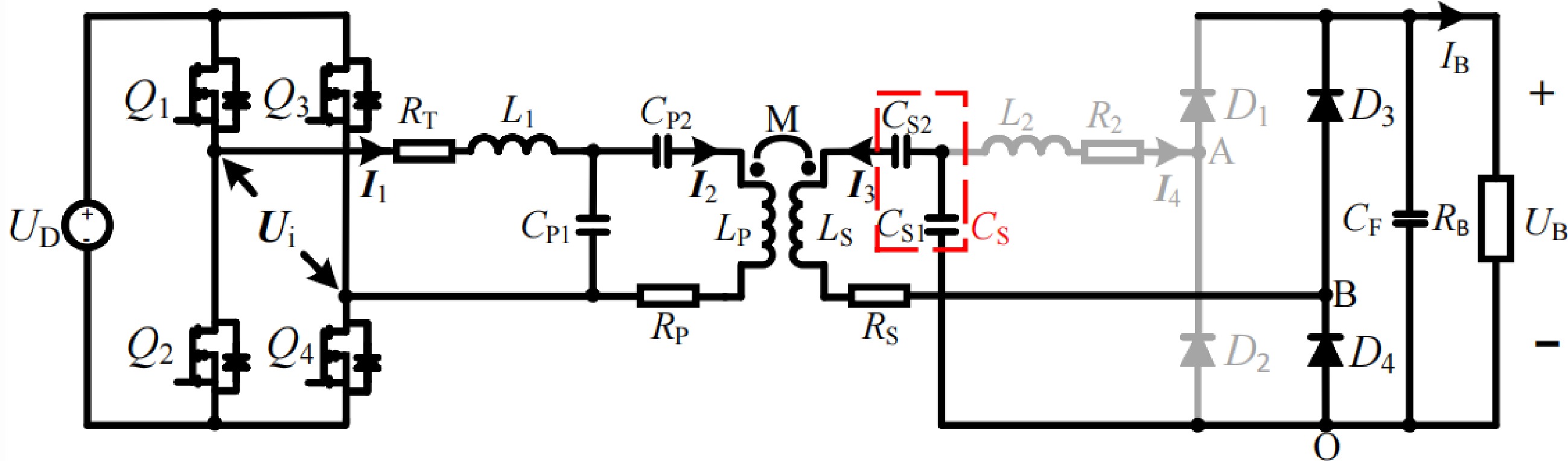
The overall circuit configuration of the proposed LCC-LCC compensated WPT system with inherent CC and CV characteristics and automatic CC-CV transition function is shown in Fig. 1, which is also the circuit configuration of CC charging. U_D is the DC input voltage. The inverter comprised of four MOSFETs (Q₁, Q₂, Q₃, and Q₄) is applied to supply the LCC-LCC resonant tank. L_P, L_S, and M stand for the self-inductances of transceiver-side coils and the corresponding mutual inductance. L_1, C_P1, and C_P2 are the compensation inductance and capacitances on the transmitter. The special receiver-side LCC resonant tank composed of the compensation inductance L₂, compensation capacitances C_S1 and C_S2 are utilized to obtain the automatic CC-CV transition function. R_T, R_P, R_S, and R₂ stand for the corresponding parasitic resistances of L₁, L_P, L_S, and L₂, respectively. In the initial stage of charging, the CC mode is performed, the proposed system operates in the LCC-LCC resonant tank with inherent CC characteristics, as shown in Fig. 1. As charging progresses, the battery voltage continuously increases. At the CC-CV transition point, the battery voltage is just higher than the voltage across C_S1, diodes D₁ and D₂ are forced to reverse bias. Then, the proposed system automatically converts to LCC-S resonant tank with inherent CV characteristics. The associated circuit configuration of the proposed system for CV charging is depicted in Fig. 2.

Figure 1.  Overall circuit configuration of proposed WPT system and circuit configuration of the LCC-LCC compensated WPT system for CC charging.

DownLoad: Full-Size Img PowerPoint

Figure 2.  Circuit configuration of the LCC-S compensated WPT system for CV charging.

DownLoad: Full-Size Img PowerPoint

Analysis of CV mode

In CV mode, since the battery voltage is higher than the voltage across C_S1, diodes D₁ and D₂ are forced to reverse bias, breaking the branch where L₂ is located. The proposed system operates in LCC-S topology to perform CV charging, as shown in Fig. 2. The corresponding simplified circuit diagram and equivalent circuit diagram are shown in Fig. 3a & b, respectively. According to Kirchhoff’s voltage law (KVL), Eqn (1) can be obtained.

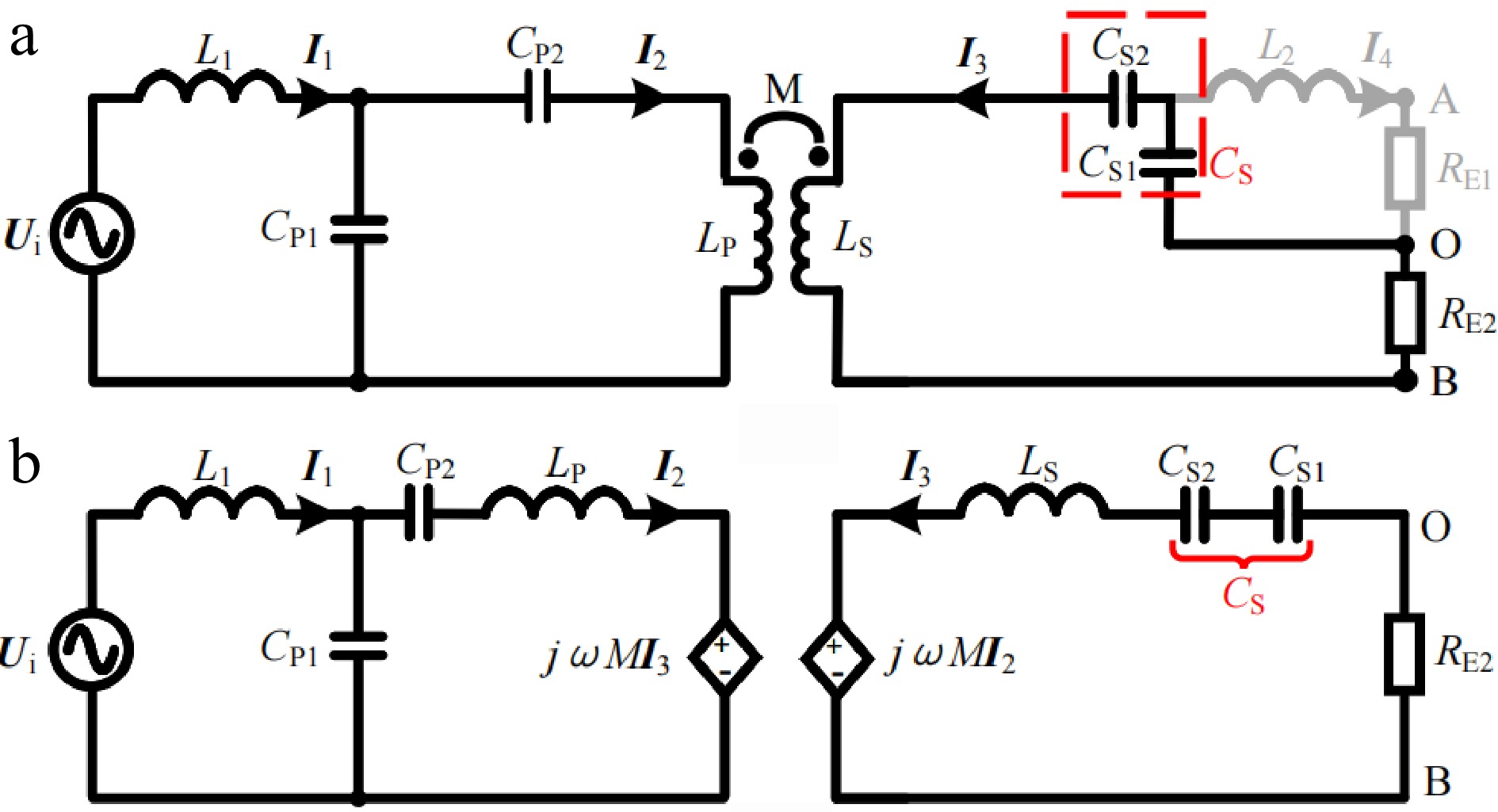
Figure 3.  Simplified circuit diagram and equivalent circuit diagram in CV mode. (a) Simplified circuit diagram. (b) Equivalent circuit diagram.

DownLoad: Full-Size Img PowerPoint

To simplify the analysis, the LCC-S topology should satisfy the following resonance conditions.

Substituting Eqn (2) into Eqn (1), Eqn (3) can be obtained.

Combining Eqn(3) and ${U_{BO}} = ({{\sqrt 2 }/\pi }){U_B}$, the charging voltage U_B can be expressed as:

where, U_i is the root mean square (RMS) value of U_i. Combining Eqn (4) and ${U_{\text{i}}} = (2\sqrt 2 /\pi ){U_{\text{D}}}$, the charging voltage U_B can be further derived as:

Observing Eqns (3) & (5), the input impedance Z_in is purely resistive and the charging voltage U_B is irrelevant to the load resistance. Therefore, the system can realize load-independent CV charging and ZPA operation. In addition, the voltage gain can be adjusted by changing the parameter of the compensation inductor L₁ to match the actual application requirements.

Analysis of CC mode

Due to the special circuit structure on the receiver, diodes D₁ and D₂ form one half-bridge rectifier, while diodes D₃ and D₄ form another half-bridge rectifier. Observing Fig. 1, the two half-bridge rectifiers have the same output terminals to power the load. Therefore, the two half-bridge rectifiers are connected in parallel. In CC mode, both the half-bridge rectifiers are activated. For the half-bridge rectifier composed of D₁ and D₂, the relationship between the RMS value of the input voltage ${U_{{\text{AO}}}}$ and the output voltage ${U_{\text{B}}}$ is ${U_{{\text{AO}}}} = (\sqrt 2 /\pi ){U_{\text{B}}}$; while for the half-bridge rectifier composed of D₃ and D₄, the relationship between the RMS value of the input voltage ${U_{{\text{BO}}}}$ and the output voltage ${U_{\text{B}}}$ is ${U_{{\text{BO}}}} = (\sqrt 2 /\pi ){U_{\text{B}}}$. Therefore, in CC mode, ${U_{{\text{AO}}}} = {U_{{\text{BO}}}}$. To simplify the circuit analysis, the parasitic resistances R_T, R_P, R_S, and R₂ are ignored. The simplified circuit of the LCC-LCC compensated WPT system for CC charging is depicted in Fig. 4a. R_E1 is the equivalent resistance between the A and O terminals, R_E2 is the equivalent resistance between the B and O terminals. Also as the two half-bridge rectifiers are connected in parallel, the relationship between R_E1, R_E2, and R_B can be expressed as:

To make the CC analysis process easier to understand, the corresponding equivalent circuit diagram is provided, as shown in Fig. 4b. Assuming that C_S1 and L₂ represented in gold satisfy the resonance condition $j\omega {L_{\text{2}}} + 1/j\omega {C_{{\text{S1}}}} = 0$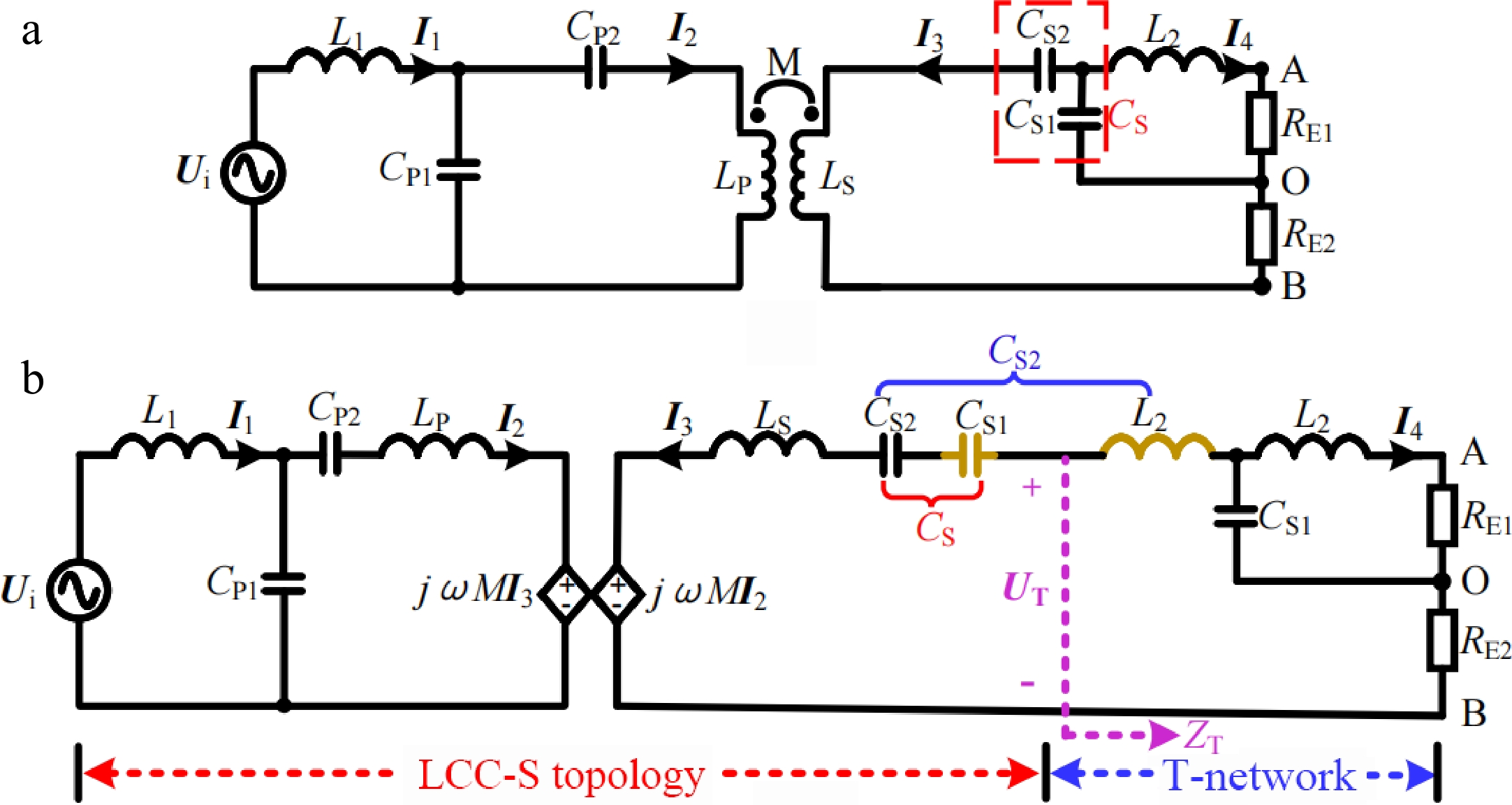, C_S1 and L₂ are equivalent to being short-circuited. Therefore, the part enclosed by the blue curly brackets in Fig. 4b is equivalent to C_S2. Through the above analysis, the proposed LCC-LCC topology can be equivalent to the cascade of the LCC-S topology and the special T-network. Among them, the output voltage of the LCC-S topology is also the input voltage of the special T-network, which is set as U_T. In addition, the output impedance of the LCC-S topology is also the input impedance of the special T-network, denoted as Z_T.

Figure 4.  Simplified circuit diagram and equivalent circuit diagram in CC mode. (a) Simplified circuit diagram. (b) Equivalent circuit diagram.

DownLoad: Full-Size Img PowerPoint

Based on the analysis of the LCC-S topology for CV charging in section Analysis of CV mode, the following Eqn (7) can be concluded:

Then, the special T-network in Fig. 4b is analyzed. According to KVL, Eqn (8) can be obtained:

Combining ${U_{ {\text{AO}}}} = {U_{{\text{BO}}}}$,$j\omega {L_{\text{2}}} + 1/j\omega {C_{{\text{S1}}}} = 0$, Eqns (6) & (8), Eqn (9) can be derived:

From Eqn (9), the equivalent output current I_O of the special T-network, which is also the RMS value of the two half-bridge rectifiers’ equivalent input current, can be deduced as:

According to Eqn (10), it can be concluded that a CV source can be transformed into a CC source through the special T-network shown in Fig. 4b. Further, combining Eqns (7), (9), (10) and ${U_{\text{i}}} = (2\sqrt 2 /\pi ){U_{\text{D}}}$, the charging current I_B and the input impedance Z_in can be calculated as:

As evident from Eqn (11), the input impedance Z_in is purely resistive and the charging current I_B is irrelevant to the load resistance. Therefore, the system can achieve load-independent CC charging and ZPA operation. In addition, the transconductance gain can be adjusted by changing the parameters of compensation inductors L₁ and L₂ to match the actual application requirements.

Experimental validation

Experimental prototype

To verify the practicability of the proposed method, an experimental prototype is fabricated, as shown in Fig. 5. Given an electric bicycle on-board battery pack with nominal voltage of 72 V and capacity of 20 Ah, the required charging current I_B in CC mode and charging voltage U_B in CV mode can be set to 3.2 A and 80 V, respectively. Four MOSFET (IRF530) are selected to form the inverter, and four diodes (MBR16100CT) are chosen to construct the rectifier. The feasibility of adopting a resistive load to replace the battery has been experimentally demonstrated in detail in a study by Chen et al.^[19]. Thus, this study utilizes the resistive load to conduct experimental testing. The operating frequency f is set to 85 kHz. A DC input voltage U_D of 40 V is applied to supply the system. Subsequently, through the above theoretical analysis, the parameters of each compensation component can be set reasonably by Eqns (2), (5), (11) and $j\omega {L_{\text{2}}} + 1/j\omega {C_{{\text{S1}}}} = 0$. The specific circuit parameters of the proposed LCC-LCC compensated WPT system are listed in Table 1.

Figure 5.  Experimental prototype.

DownLoad: Full-Size Img PowerPoint

Table 1.  Specific circuit parameters of the proposed LCC-LCC compensated WPT system.

Parameters	Value	Parameters	Value	Parameters	Value
UD	40 V	LP	100.3 uH	CP1	175.4 nF
UB	80 V	LS	100.1 uH	CP2	34.9 nF
IB	3.2 A	L1	19.8 uH	CS1	365.2 nF
f	85 kHz	L2	9.6 uH	CS2	38.8 nF
M	20.4 uH	RP	0.12 Ω	RS	0.1 Ω

 | Show Table

DownLoad: CSV

Experimental results

In the initial stage of charging, the proposed system performs the CC charging with an LCC-LCC resonant tank. The measured experimental waveforms in CC mode when the battery equivalent resistance R_B is about 5 and 10 Ω are shown in Fig. 6a & b, respectively. Observing the two figures marked with Oscilloscope 1, the charging current I_B roughly maintains a constant value of 3.2 A when R_B varies, which demonstrates the load-independent CC output characteristic. In addition, U_i and I₁ are basically in phase, indicating that the system can achieve ZPA operation in CC mode. Then, from the two figures marked with Oscilloscope 2, the RMS values of the two rectifiers’ input voltages U_AO and U_BO are equal, which verifies the correctness of the two rectifiers working in parallel in CC mode. In addition, as R_B increases, I₄ gradually decreases and I₃ gradually increases. I₃ and I₄ are rectified and output in parallel to form a CC source. Furthermore, from the two figures marked with Oscilloscope 3, the battery voltage U_B is lower than the peak value of U_CS1 (the voltage across C_S1) in CC mode. Diodes D₁ and D₂ are both in the conduction state, forming the current I₄.

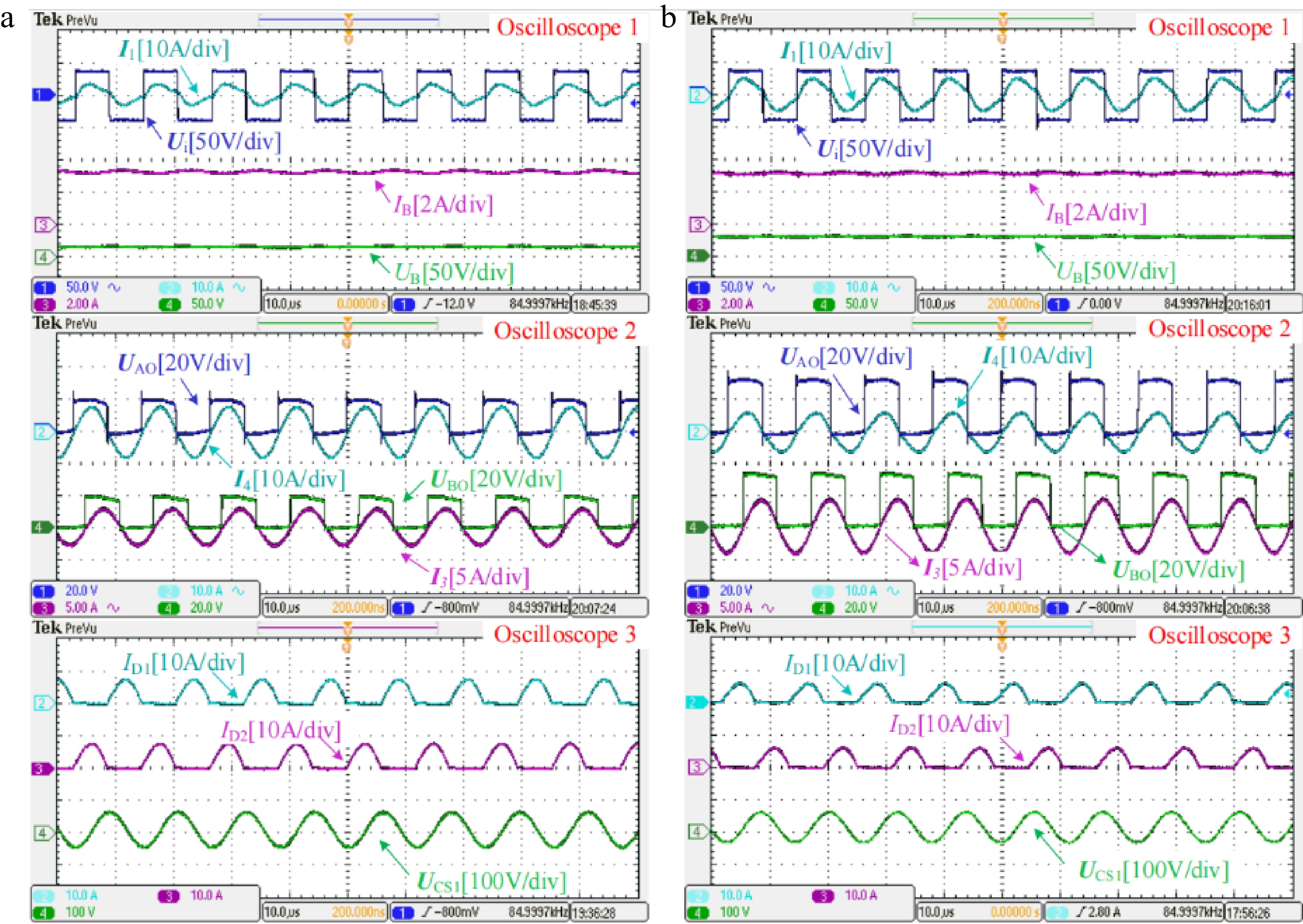
Figure 6.  Measured experimental waveforms in CC mode when the battery equivalent resistance R_B is about (a) 5 Ω and (b) 10 Ω, respectively.

DownLoad: Full-Size Img PowerPoint

As charging progresses, when U_B rises close to the peak value of U_CS1, the CC-CV transition is automatically performed. The measured experimental waveforms at the CC-CV transition point when R_B is about 25 Ω are shown in Fig. 7. Observing the figure marked with Oscilloscope 1, U_B, and I_B are slightly lower than preset values and the ZPA operation can be achieved. Then, from the figure marked with Oscilloscope 2, U_AO and U_BO are approximately equal. I₄ is very small, which means the branch where L₂ is located is about to be cut off. Furthermore, from the figure marked with Oscilloscope 3, U_B is close to the peak value of U_CS1, diodes D₁, and D₂ are both in an extremely weak conduction state, forming the weak current I₄, and the system is about to transition from LCC-LCC topology for CC charging to LCC-S topology for CV charging.

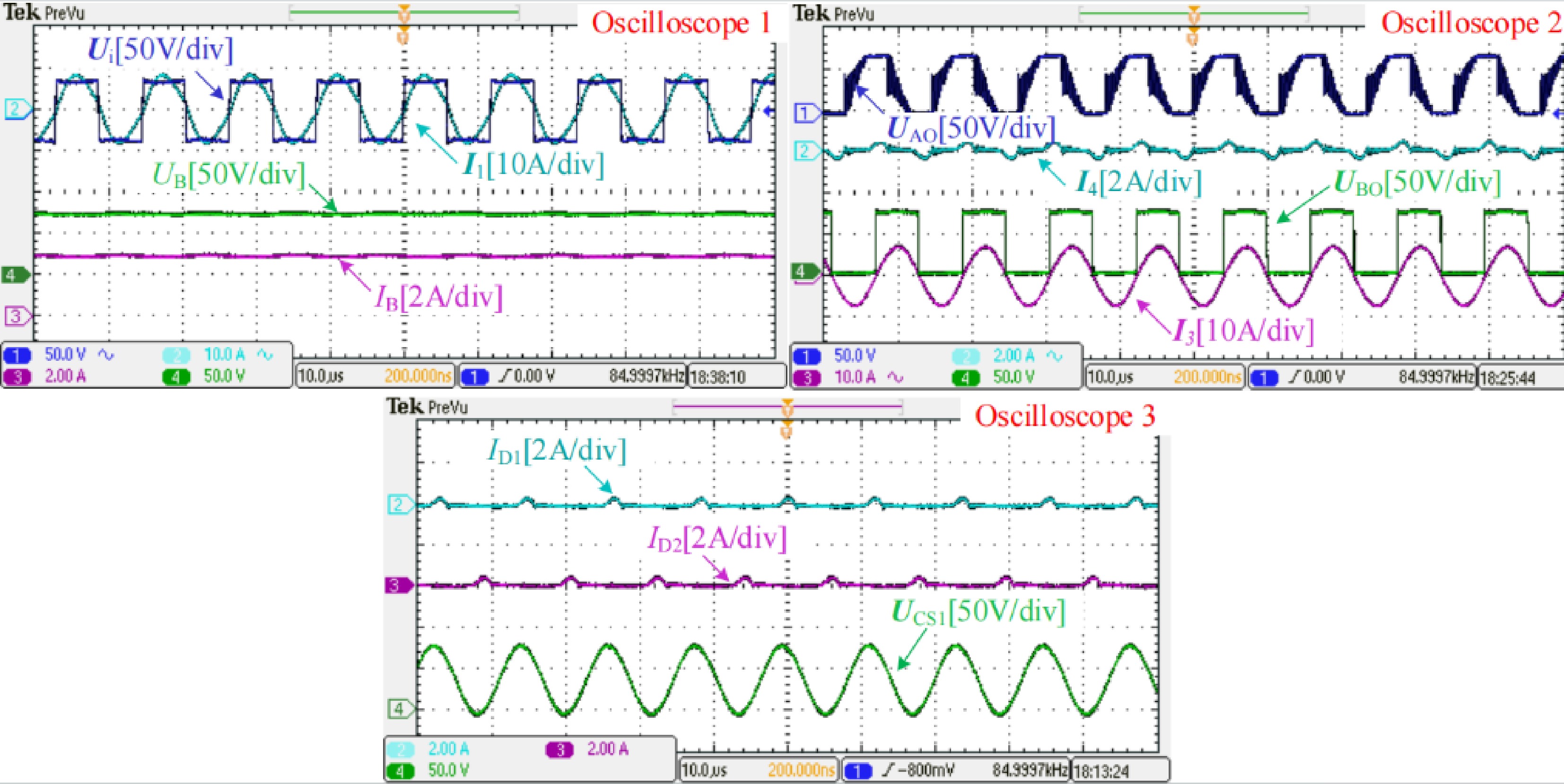
Figure 7.  Measured experimental waveforms at the CC-CV transition point when the battery equivalent resistance R_B is about 25 Ω.

DownLoad: Full-Size Img PowerPoint

As the battery voltage continues to rise when U_B is higher that the peak value of U_CS1, diodes D₁ and D₂ are forced to reverse bias. The branch where L₂ is located is completely cut off. Then, the proposed system performs the CV charging with LCC-S resonant tank. The measured experimental waveforms in CV mode when R_B is about 70 and 140 Ω are shown in Fig. 8a & b, respectively. Observing the two figures marked with Oscilloscope 1, the charging voltage U_B roughly maintains a constant value of 80 V when R_B varies, which demonstrates the load-independent CV output characteristic. The phase of I₁ is approximately consistent with that of U_i, which indicates that the system can achieve ZPA operation in CV mode. Then, from the two figures marked with Oscilloscope 2, as diodes D₁ and D₂ are reverse biased to break the branch where L₂ is located, the current I₄ drops to zero. Only the rectifier composed of D₃ and D₄ supplies power to the load. In addition, since the branch where L₂ is located is cut off, U_AO and U_CS1 will remain the same, which can be found by comparing the figures marked with Oscilloscopes 2 and 3. Furthermore, from the two figures marked with Oscilloscope 3, the currents flowing through diodes D₁ and D₂ are both 0, which is consistent with the current I₄, verifying that the branch where L₂ is located is completely cut off. In addition, as R_B increases, the peak value of U_CS1 decreases gradually, and the system will operate normally with LCC-S topology for CV charging until the end of charging.

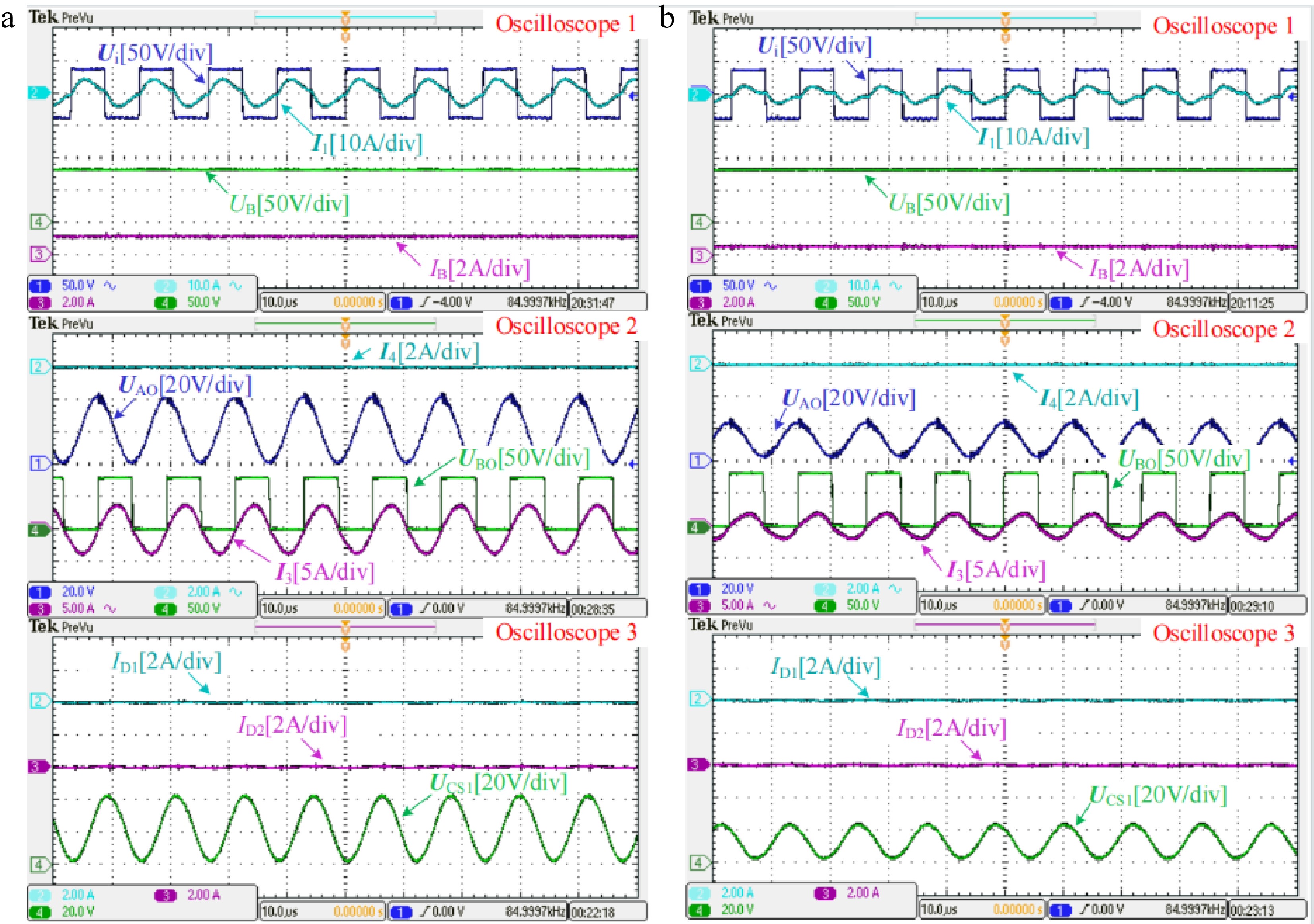
Figure 8.  Measured experimental waveforms in CV mode when the battery equivalent resistance R_B is about (a) 70 Ω and (b) 140 Ω, respectively.

DownLoad: Full-Size Img PowerPoint

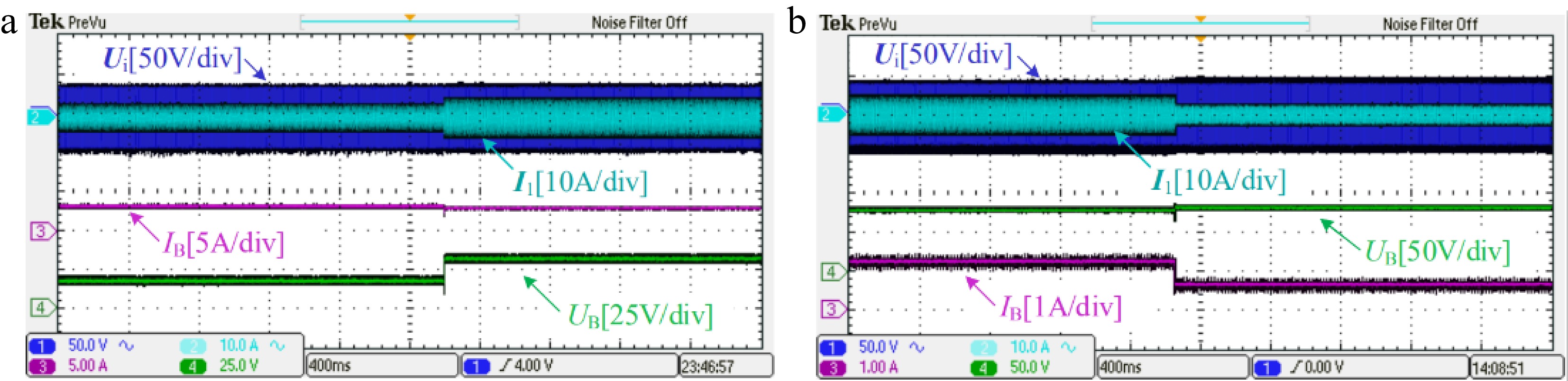
Transient results with R_B step changes from 5 to 10 Ω in CC mode and from 70 to 140 Ω in CV mode are tested respectively, as shown in Fig. 9. From Fig. 9, when R_B is suddenly increased by 100%, the resulting changes in both charging current I_B in CC mode and the charging voltage U_B in CV mode are very small. In addition, there is no significant overshoot when R_B is changed suddenly in both CC and CV modes. This further validates that the proposed system can perform CC and CV charging stably.

Figure 9.  Transient results with load step changes (a) from 5 to 10 Ω and (b) from 70 to 140 Ω.

DownLoad: Full-Size Img PowerPoint

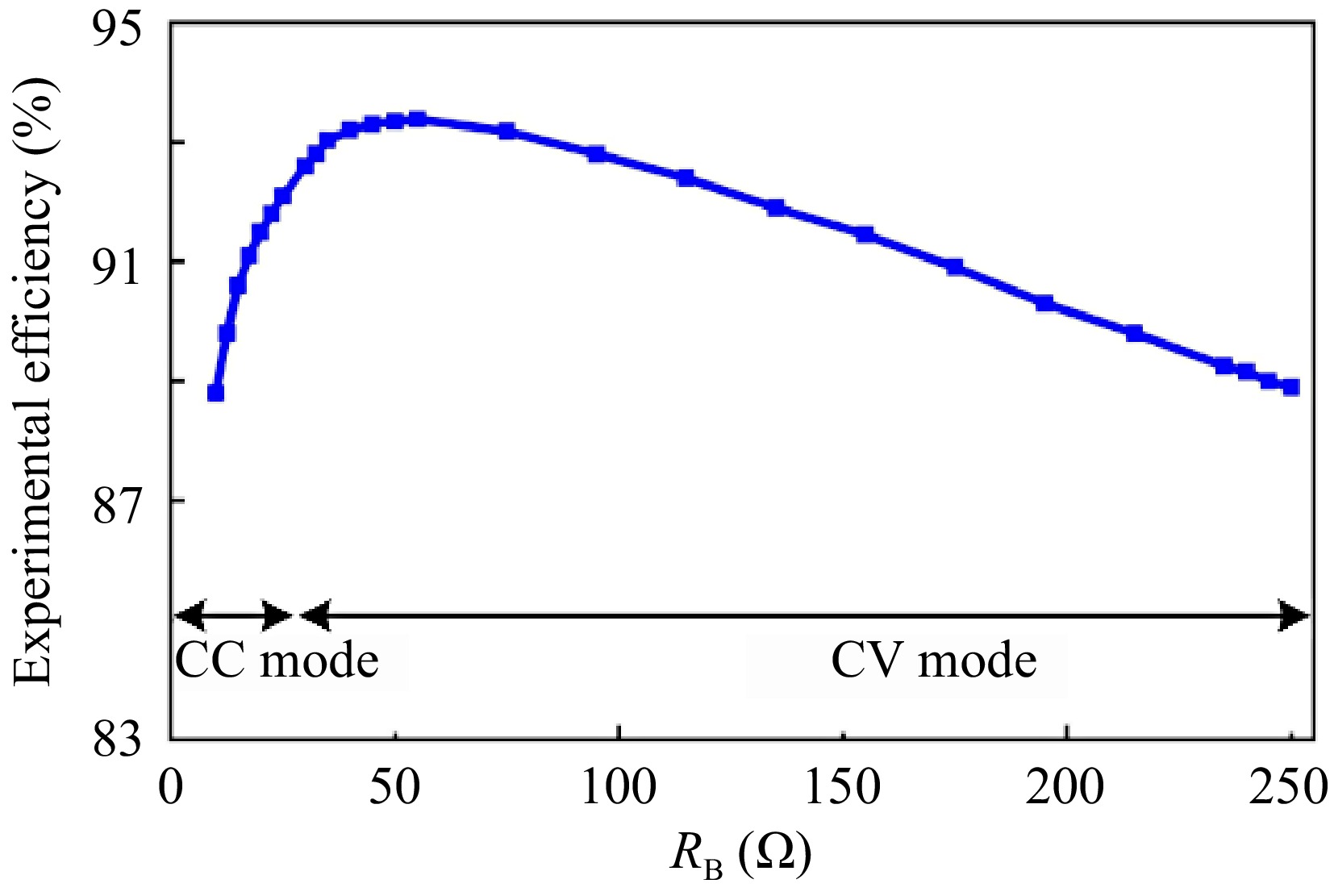
Figure 10 shows the DC-DC efficiency curve of the proposed system during the whole charging process. In CC mode, as R_B varies from 10 to 25 Ω, the system efficiency climbs up from 88.8% to 92.1%. In CV mode, as R_B varies from 25 to 250 Ω, the system efficiency slowly drops from the peak of 93.38% to 88.9%. The proposed system maintains high efficiency throughout the charging process.

Figure 10.  DC-DC efficiency curve of the proposed system during the whole charging process.

DownLoad: Full-Size Img PowerPoint

Table 2.  System configuration and cost comparison with existing popular methods

Proposed in	Ref. [10−13]	Ref. [14−18]	This study
Method	Hybrid topology switching	Dual-frequency switching	Automatic CC-CV transition
Without detection circuits	No	No	Yes
Without communication links	No	No	Yes
Without open-circuit protection circuits	No	No	Yes
Without excess components and switches	No	Yes	Yes
Cost	High	Medium	Low

 | Show Table

DownLoad: CSV

To reflect the low cost of the proposed system more intuitively, the configuration and cost of the proposed system are compared with currently popular hybrid topology switching and dual-frequency switching methods, as shown in Table 2. Considering hardware requirements such as detection circuits for CC-CV transition, communication links, open-circuit protection circuits, and excess components and AC switches and the corresponding driving circuits, the proposed system performs best from the perspective of cost-effectiveness.

Conclusions

In this paper, an LCC-LCC compensated WPT system with inherent CC and CV characteristics and automatic CC-CV transition function are put forward for battery charging applications. CC and CV characteristics under the corresponding circuit configurations are analyzed in detail. The feasibility of the proposed system is proved by building a confirmatory prototype, and high efficiency is maintained throughout the charging process. The features of the proposal can be summarized as follows:

(1) Compared with the closed-loop control methods, the proposed system does not need to introduce complicated control algorithms, which reduces the difficulty of controller design and is easy to implement.

(2) Compared with the hybrid topology switching method, the proposed system does not require additional passive components, AC switches, and corresponding driving circuits, which simplifies the system structure.

(3) Compared with the dual-frequency switching method, the proposed system runs at a fixed frequency, which avoids the frequency bifurcation phenomenon and has high robustness.

(4) In addition, the proposed system can automatically realize the transition from CC to CV mode through its structural properties, without additional detection circuits, communication links, and open-circuit protection circuits, which makes the system simpler and less costly.

Author contributions

The authors confirm contribution to the paper as follows: study conception and design: Zhou X; data collection: Wang Y; analysis and interpretation of results: Zhou X, Yang L; draft manuscript preparation: Zhou X, Wang Y. All authors reviewed the results and approved the final version of the manuscript.

Data availability

All data generated or analyzed during this study are included in this published article.

Acknowledgments

This work was supported in part by the following: Scientific Research Youth Foundation of Hunan Province Education Department of China (22B0803), the Employment and Education Foundation of The Second Phase of The Department of College Students of The Ministry of Education of China (20230106677), the Guiding Science and Technology Programme Foundation of Yongzhou City of China (2022-YZKJZD-010), and the Natural Science Foundation of Hunan Province (2024JJ7186).