-
The human benefits of man-plant interactions are mainly associated with economic, environmental, health and well-being aspects. We can focus on these types of functional benefits in addition to the benefits of the plants themselves (e.g., visual physiognomies, insect and/or disease endurance, cold or heat toleration, salt-water allowance, endurance to deficiency, etc.). Humans would better comprehend the intrinsic ways that plants enhance the quality of their lives and begin to perceive plants as a necessity in their lives rather than just a luxury. Along with these beneficial effects of plants, human-plant interactions can produce undesirable effects for plants. This is the case for various pollutions resulting from daily human activities.
In general, a whole plant or one of its parts such as a leaf, stem, root, fruit, etc. could be a horticultural product. Ornamental plants are horticultural products whose purpose is mainly decorative, just as vegetables are mainly edible. Ornamentals compose a great and varied assembly of entire plants or shares of plants commonly developed for decorative commitments. Ornamental can be congregated into cut flowers, ornamental greenery, tubers, rhizomes, etc. Many of these are sensitive to cold and water loss. Ornamental plants, which are also commonly garden plants, are often grown near areas of human activity. Daily electromagnetic devices increasingly occupy this environment. Many of these tools, such as antennas, chargers, cell phones, and cell phones towers operate wirelessly which often generate stray fields. Radiated electromagnetic fields (EMFs), which are typically in the non-ionizing radio frequency (RF) range or other, interact with surrounding environmental objects[1−6]. These objects could be human tissue as well as non-human species such as birds, bees, plants, animals, etc.[7, 8]. Exposure to EMF behaves as an environmental stressor causing biological effects. EMF exposures can be caused by artificial tools, but also by natural accidental phenomena such as lightning or by accidental malfunction of electrical devices. These exposures can behave in near field or far field mode depending on the distance between the exposure source and the exposed tissues. The exposure nature in these two situations are very different. In the near field case (as e.g. a cell phone touching a body), the exposure is focused on a restricted part of the body tissue, while for the far field (e.g. a cell phone antenna tower), the exposure is homogenous overall the body tissues. The biological effect (BE) is closely linked to the nature of the EMF, the physical and geometric properties of the tissues as well as the exposure conditions and intervals[9]. Typical BE is thermal, resulting in an increase in temperature of exposed tissues[10]. This effect is due to the dissipated EMF energy and characterized by the specific absorption rate (SAR) expressed in power per mass unit, and the duration of exposure in the exposed material. For higher SAR values and longer durations, the dissipated energy can cause excessive heating, which can trigger, depending on the tissue, molecular alterations (non-thermal effects)[7].
In the field of plants, various work has been carried out concerning the histology and the effects of plant stress factors[11−21]. This research covered various applications on specific species using different analysis tools. These works will be commented in the different sections of this contribution.
This contribution aims to propose an approach to study the BEs of RF-EMF exposure of plants. Such an approach intends to take into account the nature of the exposure source, the properties of the exposed subject and the exposure conditions. It targets to predict, monitor and stipulate ways of protection against exposure. The section - Thermal BE and tissue anatomy - analyzes the thermal BE and the plant tissues anatomy. Through a parallel exploration of animal and plant, the fluids circulating in plant vessels are discussed and illustrated. The section - Governing equations - introduces and analyzes the electromagnetic and the heat transfer equations governing thermal BE due to exposure to EMFs. The section - Supervising and protection of EMF effects - concerns the supervising and protection of EMF radiation effects. The section - Conclusions - ends the paper by conclusions and recommendations for future work. The proposed contribution is supported by a literature review of the different topics involved.
-
Regarding tissue properties, geometries with higher surface-to-thickness ratios and lower tissue perfusion rates could make the subject more vulnerable. This situation can concern parts of ornamental plants and thus justifies the predictive control of exposure to EMFs[11, 12]. For understanding such problems, one must study the anatomy of tissues, i.e. histology science[13]. Histology is the science that studies the anatomy of tissues. Body tissue is a combination of cells working together and having a similar function. A multicellular organism is constituted of different sets of cells associated together forming a tissue. In general, tissues are built of several cell types that meet different needs for tissue function. Microscopic histology of biological sciences allows classification of plant and animal tissues and the identification of their itemized organization. Biological tissue of a plant consists of a certain number of cells performing a specific function. For example, the plant epidermis is the tissue providing its protection and vascular plant tissues are involved in transporting nutrients throughout the plant body.
In a similar manner, plants and animals live, feed, excrete, breathe, grow, etc. and are sensitive to the environment. Plant and animal vascular tissues transport water and nutrients in plants and oxygen and nutrients in animals.
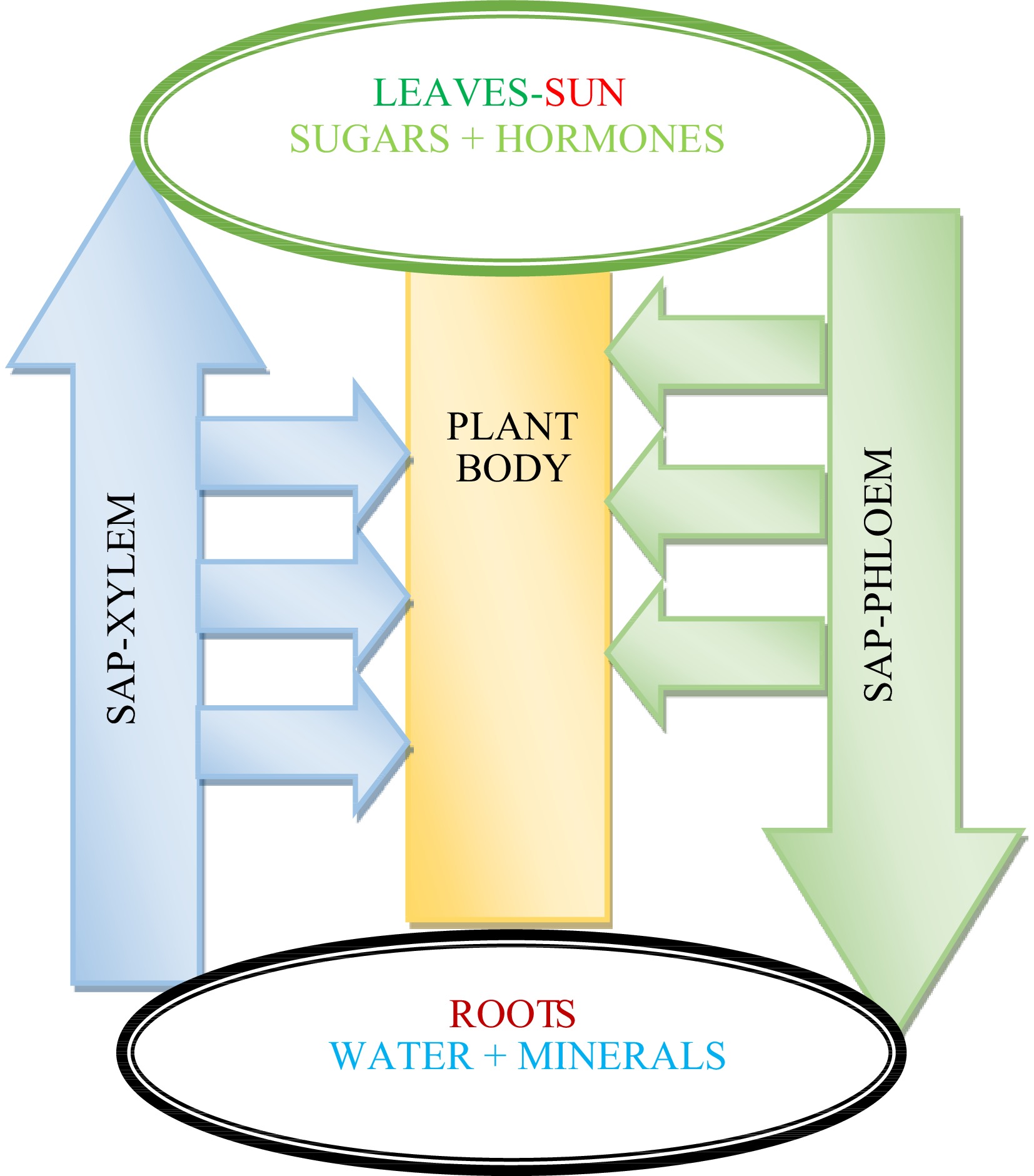
Plant sap plays the same role in plants as blood in animals. Two types of sap fluids circulating in two corresponding vessel types of the plant in opposite directions (leaves to roots and vice versa). Phloem primarily transports sugars and hormones from leaves to roots throughout the plant and xylem primarily transport water and minerals in the opposite direction. They act as arteries and veins as in animals. Note that sugars and hormones are produced by the interaction of leaves and sunlight while water and minerals are filtered and absorbed by roots from soil. Figure 1 schematically illustrates the role of sap fluids in relation to the different parts of a plant.
It should be noted that the thermal BE due to EMF exposure is different from heating resulting from ambient warm air. The latter occurs by conduction via the surface of the plants and regularly these behave in such a way as to protect themselves from such heating thanks to the protection of the epidermal tissues. The epidermis is the outer tissue of the plant, which covers its surface protecting the internal layers from the external environment. A layer of waterproof cuticle covers the epidermis thus preventing water loss to maintain acceptable perfusion rates. The epidermal tissue protects the plant from ultraviolet rays but allows gas exchange with the exterior via a network of stomatal pores. The stoma is a small orifice present in the epidermis and composed of two guard cells forming a stomatal pore. Heat stress, in this case, can disrupt ornamental plants in various ways depending on the individual species and their thermal tolerance. High temperatures can lead to decreased photosynthesis and weakened pollen growth and durability, while low temperatures can lead to slowed growth and late flowering. These heat effects seem well self-mastered by plants[14−18].
The RF-EMF heating happens directly inside the tissues like in microwave heating[10]. Two characteristics fix such occurrence. The first relates to the ability of RF energy to heat swiftly tissues[9]. The second is linked to the weakness of the tissues to withstand the erratic increase in temperature that can occur. Note that the parts of tissue least protected from RF-EMF are those with insufficient sap flow, which is the primary way to cope with excessive heat. The thermal effects due to RF-EMF, unlike those due to natural effects, are not well self-controlled and can disrupt the vital functions of plants[19]. Note that disproportionate and persistent fields can exhibit non-thermal effects that can alter molecular structures.
It is worthy to note that, specific EMFs interactions with plants in general as well as with human tissues could be used intentionally to solve a problem or improve behavior[20, 21]. Furthermore, the effects of RF-EMF are not well scaled and can be positive or negative for different parts of tissues and are species dependent; that is, they might be harmful to some and good to others.
-
This section is devoted to mathematical analysis of the effects of EMFs exposure. The electromagnetic (EM) and heat transfer (HT) phenomena rule thermal BEs due to EMF exposure. The temperature increase ΔT in the tissue will be determined by the second phenomenon. The corresponding heat source will be the power dissipated in the material concerned, which can be considered by the first phenomenon. The volume density of this power Pd for dielectric materials (biological tissues) and the corresponding specific absorption rate (SAR) are given by:
$\rm P_{d} = \omega \cdot \varepsilon''\cdot E^{2}/2 $ (1) $\rm SAR = P_{d} /\rho = \omega \cdot \varepsilon''\cdot E^{2}/ (2\rho) $ (2) Equations (1, 2), the parameters: ε'' is the imaginary part of the complex permittivity of the absorbing material and ρ (in kg/m3) is the material density. The variable ω is the angular frequency = 2πf, f is the frequency (Hz) of the exciting EMF, E the absolute peak value of the electric field strength (V/m) and SAR (in W/kg). The power dissipation (in W/m3) given by Eqn (1) relates to foremost dielectric heating of EMF energy loss. Note that the imaginary part ε'' of the (frequency-dependent) permittivity ε (in F/m) is a measure for the ability of a dielectric material to convert EMF energy into heat, also named dielectric loss. The real part ε' of the permittivity is the normal effect of capacitance and results in non-dissipative reactive power.
The power dissipations given by Eqn (1) as well as the SAR given by Eqn (2) will be used in the coupling of EM and HT equations.
The governing equations are the Maxwell EM equations[22] and the HT adapted plant bio-heat tissue equation. The junction between EMF and ΔT is Pd or SAR, which can be obtained from EM equations and used as input to the HT equation.
EM equations
-
The system of EM equations can be formulated mathematically in different functional forms of the problem considered. One of the most common is the basic full-wave electromagnetic formulation for harmonic fields, which seems simpler to explain. The EM equations can be given by:
$ \bf\bigtriangledown \times \bf H = J $ (3) $ {\bf J} = \sigma {\bf E} + j \omega {\bf D} + {\bf J}_{\bf e} $ (4) $ {\bf E} = -\bigtriangledown V - j \omega {\bf A} $ (5) ${\bf B} = \bigtriangledown \times {\bf A} $ (6) In EM Eqns (3–6), H and E are the magnetic and electric fields in A/m and V/m, B and D are the magnetic and electric inductions in T and C/m2, A and V are the magnetic vector and electric scalar potentials in W/m and volt. J and Je are the total and source current densities in A/m2, σ is the electric conductivity in S/m, and ω is the angular frequency. The symbol
$\bigtriangledown $ The input source term in EM Eqns (3−6) is the excitation current density Je = σ Ee = j ω De = j ω ε Ee. The choice of the form of the source term depends on the nature of the exposure, near or far field, see the section - EMF-PBH model solution strategy - relative to the solution technique.
The dissipated power Pd and the SAR given by Eqns (1 and 2) can be determined via the E value obtained from the solution of Eqns (3−6).
HT equations
-
Considering the HT problem, in general the amount of heat quantity absorbed by an element of tissue or more generally of a lossy dielectric can be given as:
$\rm \Delta Q = c m_{s} \Delta T $ (7) In Eqn (7), Q is the heat energy absorbed or dissipated in joule (J), ms is the mass of the substance in (kg), ΔT is the change in substance temperature in (°C), c is the specific heat of the substance (the heat required to change a substance unit mass by one degree) in J/(kg °C). The corresponding power will be ΔP = ΔQ/ Δt. The volume specific power will be:
$\rm \Delta P_{v} = \Delta P/ v = c (m_{s} /v) (\Delta T/\Delta t) = c \rho (\Delta T/\Delta t) $ (8) In Eqn (8), P is the power in watt (W), t is the time in (s), Pv is the power per unit volume in (W/m3), v is the volume in m3, and ρ is the density in kg/m3.
The HT equation giving the volume specific power of Eqn (8) in its differential form is given by:
$\rm c \rho \partial T/\partial t = \bigtriangledown \cdot (k \bigtriangledown T) $ (9) In Eqn (9), k is thermal conductivity in W/ (m∙°C)
Considering the case of tissues in plants, we have to consider in Eqn (9) the internal heat source Pi and the involved convective heat transfer via sap fluid corresponding to the considered part of the plant (leaf, flower petal, stem, branch, trunk, etc.). The convective heat transfer coefficient in the sap hs in W/(m2∙°C) can be defined through ΔP = hs S ΔT and from Eqn (8):
$\rm \Delta P_{v} = h_{s} (S/v) \Delta T = (h_{s} / \chi) \Delta T = c_{s} \rho_{s} (\Delta T/\Delta t) $ (10) Then:
$\rm h_{s} = c_{s} \rho_{s} p_{s}\chi $ (11) In Eqns (10, 11), S is the surface of plant part concerned in m2, χ is the thickness of the plant part in m. Also cs, ρs, ps are respectively sap, specific heat in in J/(kg °C), density in kg/m3, perfusion rate in 1/s. Note that in the present work the vulnerable exposed plant parts are mostly leaves and flower petals.
On the other hand, we have to consider in Eqn (9) the external heat source related to the EMF exposure, Pd or SAR given by Eqns (1 and 2).
Under these conditions, Eqn (9) will be extended to a plant bio-heat (PBH) equation, which could be presented as follows:
$\rm c \rho \partial T/\partial t = \bigtriangledown \cdot (k\; \bigtriangledown T) + P_{d} + P_{i} + c_{s} \rho_{s} p_{s} (T_{s} - T) $ (12) In Eqn (12), Pi is the tissue internal (latent heat flux) heat source in W/m3, Ts and T are respectively the sap fluid temperature and the local temperature of tissue in °C. Equation (12) corresponds to a bio-heat plant tissues accounting for EMF exposure. This equation has a form similar to the Penne’s bio-heat equation[9, 10, 23] related to human tissues and convective heat transfer in blood. As mentioned earlier, plant sap plays the role of blood in animals. In addition, phloems and xylems for sap play the role of arteries and veins for blood. Note that in Penne’s bio-heat equation, the term related to tissues metabolic heat corresponds to plant tissues internal heat in Eqn (12). As well, the terms representing convection heat transfer correspond respectively in the two equations to animal blood and plant sap. The orders of magnitude of the relative values of the parameters related to animal and plant tissues as well as blood and sap are obviously different due to the different nature of animal and plant tissues. The different values of parameters involved in Eqn (12) relative to Pi, cs, ρs, and ps depend on the plant type and the specific part of this plant. These values could be found in textbooks or could be measured.
EMF-PBH model solution strategy
-
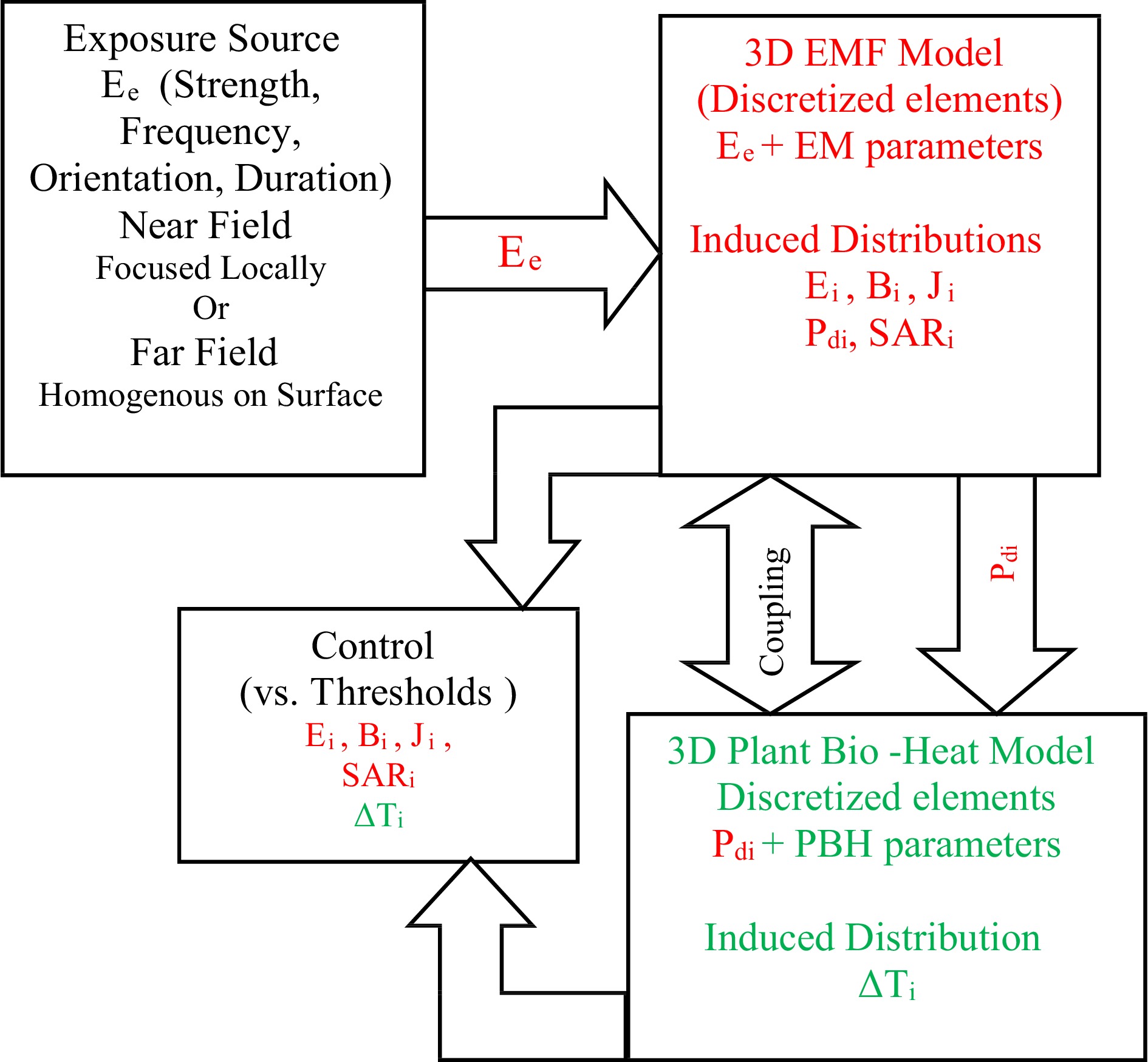
Equations (3–6 and 12) can be solved in a coupled way. Given the geometric complexity and inhomogeneity of tissue, the solution must be local in the tissue using discretized 3D techniques as finite elements[24−30] in the appropriate element of the tissue. The discretized 3D elements are volume parts enclosed in surface elements, each encircled by edge elements, each ended by two nodes. For example, a tetrahedral element involves four triangular faces, six straight edges, and four nodes. The fields could be defined on nodes, edges, faces or volume depending on the nature of the field as requirements of continuity, etc.[31]. The coupling of the EMF and PBH equations is weak in nature due to the distant values of their time constants[9,10,23]. Thus, an iterative solution provides in the tissue the local distributions of the induced values of E, B, and J, and hence Pd, SAR, and ΔT. The parameters concerned are those of the tissue properties, ε, Pi, cs, ρs, ps, etc. The geometry involved is that related to the shape of the portion of tissue concerned. Exposure conditions are taken into account via the nature of the EMF source (strength and frequency) and the exposure interval. Note that consideration of the exposure source is different for near or far field cases. For near-field radiation, the source is generally involved in the solution domain as a focused field. In the case of the far field, which is generally of homogeneous value, the source is imposed uniformly over the entire exposed surface of the object. Figure 2 summarizes the EMF-PBH models, weak coupled solution strategy accounting for the nature of the exposure source and the tissue parameters. The induced fields are controlled vs thresholds in the whole tissue.
-
The obtained local 3D distributions regarding the induced EMFs and ΔT make it possible to accomplish two main actions, which are the control of the effects (Fig. 2) as well as the protection strategies concerning the radiated fields.
Plant adverse effects and EMF features
-
First, we will summarize the main adverse effects on plants due to exposure to EMFs as well as the features of the last.
As mentioned previously, high-frequency EMF heating focuses directly inside tissues, such as during microwave (MW) heating[10]. Additionally, high frequencies such as in the RF and MW range reflect an energetic capacity to, rapidly heat tissues[9]. Added to this is the weakness of the tissues to resist the erratic increase in temperature, which can occur particularly in those parts of the tissues where the flow of sap is insufficient, which constitutes the main means of coping with excessive heat. These three traits, inner focus, rapid heating, and low sap flow, are not programmed into the plant's natural self-defense, which relies on conductive and convective heat transfer relative to sunlight and warm wind. Therefore, the main negative effect on plants exposed to high-frequency EMFs would be rapid heating inside vulnerable parts of the plant, without the possibility of adequate self-defense to protect vital functions of plants[19]. Note that in addition to possible combustion of plant parts, disproportionate and persistent fields may exhibit non-thermal effects that could alter molecular structures.
The SAR given by Eqn (2) and the exposure duration Δt characterize the behaviors of EMF exposures. SAR is directly related to wave frequency, field intensity and tissue parameters. Typical SAR values for adverse effects of plant exposure are 4 to 10 W/kg. The frequency range concerned is 103 – 0.3 × 1012 Hz involving RF and MW which produce non-ionizing radiation.
Control methodology
-
In the case of human and animal tissues, the different predicted field distributions are checked by comparison to thresholds[9, 10, 23]. These thresholds are fixed in function of nature of the exposed tissue (body part, adult, child, animal, etc.), the relation of source to exposed subject (fabrication, installation, user, etc.), and the exposure condition (distance, concentration, duration, etc.). In the case of plant tissues (Fig. 2), these thresholds correspond to the safety limits of public exposure, e.g.[32, 33]. Such thresholds could be set for different, kinds of plants, parts of a plant, atmospheric circumstances of the plant location and corroborated exposure duration and conditions.
Protection strategies
-
As mentioned previously, most significant disturbances to terrestrial biodiversity are linked to nature-human interactions. This concerns fauna and flora: birds, animals, insects and plants. Ornamental plants are found in public parks, growing sites, gardens, etc. Protection of these plants against RF-EMF could be ensured by two main protection strategies. The first is directly linked to radiation sources by reducing their stray fields via shielding technologies[34−39]. This concerns not only ornamental plants, but also the entire environment, including humans, animals, electronic devices, etc. This protection strategy is not obvious and is limited by the operating principle of RF wireless devices based on the radiation of electromagnetic waves. The only way to implement such protection is to limit their emission capacity and therefore their performance in restricted protected areas. Thus, the evocation of this strategy leads us to the second protection option. This concerns the management of restricted areas devoid of radiating devices. This can concern public parks, urban districts or entire cities[40−42]. This protection option focuses largely on anthropogenic innovations and their links with biodiversity and nature.
-
In this contribution, the evaluation, discussion and analysis of disturbances due to RF-EMF exposure of ornamental plants were carried out. Review of the various concerns involved in this investigation has shown that there is continued progress in this topic. The significant characteristics raised by this subject are diverse; the most important of which are summarized as follows. The thermal BEs of RF-EMF exposure of ornamental plants could be predicted through the coupled solution of the EMF and HT equations. Such an approach makes it possible to consider the characteristics of the exposure source, the exposed subject and the exposure conditions. It helps verify and ensure protection against exposure. Due to these promises, the following various recommendations for further investigations can be encouraged:
● Explore the different categories of ornamental plants likely to be radiated by near or far fields;
● Establish (from measurements) the bio-thermal-EM parameters necessary for models of the different parts of a plant, from leaves to roots, including soils;
● Setting thresholds of EMFs: B, E, J and SAR as well as temperature rise ΔT for the main vulnerable parts of a plant.
-
The author confirms sole responsibility for the following: study conception and design, data collection, analysis and interpretation of results, and manuscript preparation.
-
All data generated or analyzed during this study are included in this published article.
-
The author declares that there is no conflict of interest.
- Copyright: © 2024 by the author(s). Published by Maximum Academic Press, Fayetteville, GA. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
-
About this article
Cite this article
Razek A. 2024. Analysis and control of ornamental plant responses to exposure to electromagnetic fields. Ornamental Plant Research 4: e009 doi: 10.48130/opr-0024-0007
Analysis and control of ornamental plant responses to exposure to electromagnetic fields
- Received: 05 January 2024
- Revised: 30 January 2024
- Accepted: 18 February 2024
- Published online: 02 April 2024
Abstract: All plants, including ornamentals, are subject to different stressors related to their environment. These can disrupt their progress, including their ability to generate pollen and reproduce successfully. These stressors may involve inert natural impacts such as temperature, deficiency and salinity levels of water. They may also involve natural active effects such as herbivores and pathogens. Other types of accidental natural effects, such as storms and lightning, could also occur. There are also artificial effects that shape the environment of human activity. Nowadays, the environment of electromagnetic fields, and in particular those at high frequency, are an important element. This contribution aims to propose an analysis and a strategy for controlling the biological effects of plant exposure to such fields. The analysis takes into account the nature of the exposure source, the properties of the exposed materials and the exposure conditions. This is accomplished through the governing equations related to electromagnetic and heat transfer phenomena permitting the prediction of biological thermal effects of the exposure. The involved coupled phenomena solution approach makes it possible to predict, verify, and provide means of protection against exposure. The proposed survey is supported by a review of the literature on the various subjects concerned.
-
Key words:
- EMF exposure /
- Daily RF devices /
- Plant tissues /
- Biological effects /
- Thermal behavior /
- EMF model /
- Bio-heat transfer model /
- Coupled strategy