-
Fruit and vegetables are prone to water loss, which is the major cause of postharvest deterioration. The symptoms of water loss are quite obvious including but not limited to shrivelling, changes in product colour, textural properties, total soluble solids, product flavour and saleable weight[1−4]. However, fruit weight loss[5,6] is a complex process involving the interaction of product morphology, physiology and environmental influence. Transpiration is the major contributing process to the mass loss of fresh produce, as demonstrated in tomatoes, pears, pomegranates, and strawberries[7−11]. Other contributing mass loss processes have been proposed including respiration and mechanisms by which ethylene gas, volatile and aromatic organic compounds are lost, depending on the climacteric or non-climacteric nature of the produce[11−14].
The majority of the water in food material exits as intra-cellular water within the confines of the cell membrane, cell wall water and inter-cellular water is locked up in the cell wall and intercellular space network, respectively[15]. Depending on transportability, inter-cellular, cell wall and intra-cellular water can be termed as free, loosely bound and strongly bound water, respectively[16]. Water moves within fresh fruit following different proposed pathways. In the Apoplastic pathway, water moves from cell to cell through the interconnected cell wall network (Apoplastic pathway), across the cell membrane (transmembrane pathway), through the continuous cytoplasmic system across adjacent cell wall openings (Symplastic pathway) through intercellular space network (Intercellular pathway)[17]. Furthermore, water movement from the tissues to the fruit surface occurs by either or a combination of convection, molecular diffusion and capillary diffusion mechanisms depending on the driving force responsible for the movement[18,19]. Convective mass transfer, molecular diffusion and capillary diffusion mechanisms are driven by pressure gradient, concentration gradient and the relative interaction of cohesive and adhesive forces between the liquid and solid phase, respectively[18,19]. At the product surface, water loss is aided and influenced by the existing numerous openings such as stomata, lenticels and micro-cracks and other structures like trichomes.
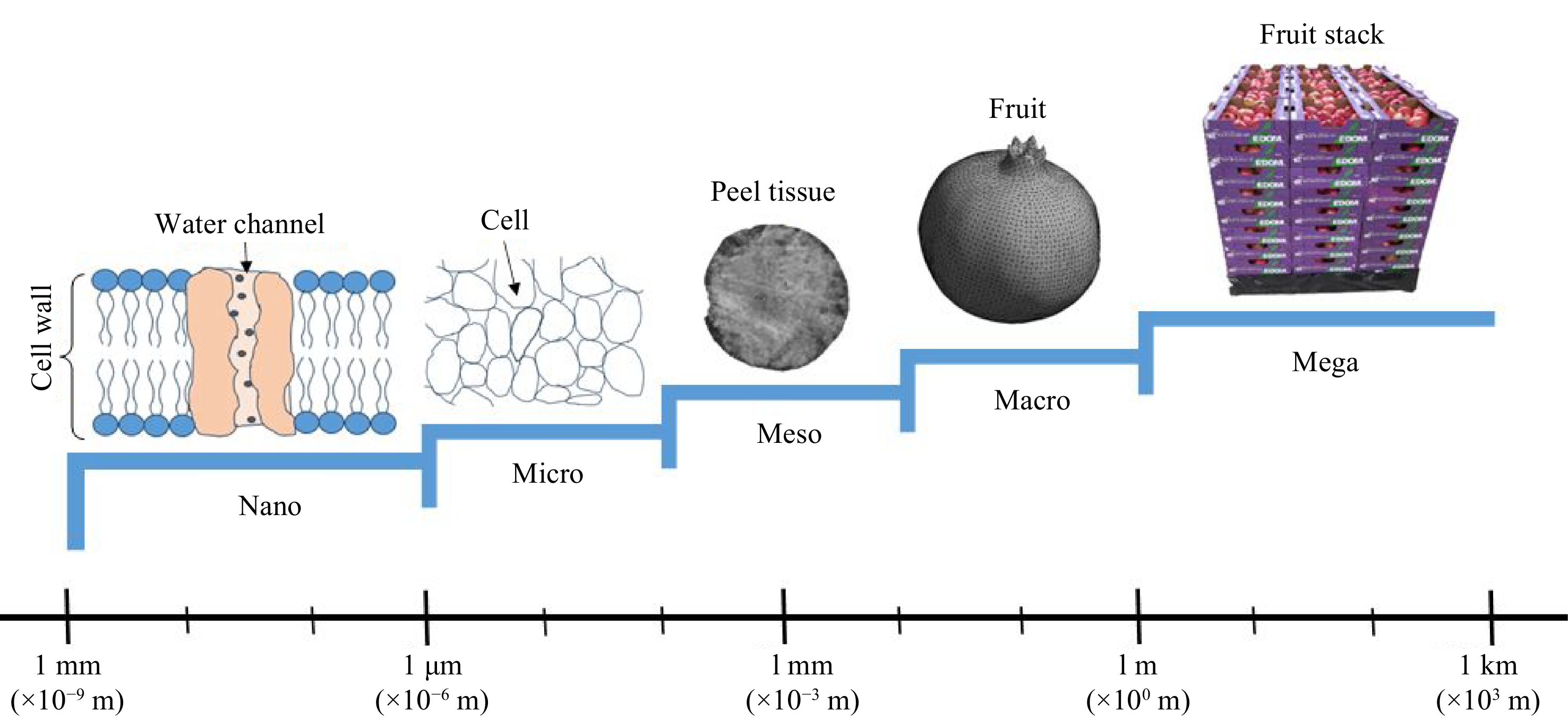
With the understanding that fruit are hierarchically structured and have features that extend from the molecular scale level to the food plant scale[20], water transport has been modelled at different spatial scales including nanoscale (e.g. Aquaporin and cell wall), microscale level (e.g. individual plant cell), mesoscale level (e.g. cortex tissue of an apple fruit) and macroscale level (e.g. whole fruit having different components)[21]. Recently, the multiscale approach is being applied which combines the details obtained through microscale and mesoscale modelling and applies them at a macroscale level. A multiscale model is a hierarchy of models describing material properties including water transport properties at different spatial scales, in such a way that the underlying sub-models are interconnected[20]. The authors carried out a detailed review on multiscale modelling. However, a knowledge gap exists in integrating the different mechanisms of weight loss into the transport models. Thus, this review aims to discuss the various mechanisms of fruit weight loss and the current modelling approach to water loss. The review pays specific attention to the physiological mechanisms of water loss, the micro and macro structure-water loss relations, the micro, macro, and multiscale approach to water loss modelling, transpiration modelling and lastly the role of imaging technologies in transport modelling.
-
Transpiration is the loss of water from the plant, plant organs like leaves and fruit or vegetables to the immediate surroundings. Weight loss from fresh produce is primarily through transpiration[22], a physiological process that continues in fruit and vegetables before and after harvest[23]. Over 97% of the total weight loss in fresh fruit and vegetables is due to transpiration[24]. In another study, net transpiration rate contributed 97.2%, 95.8% and 77.8% of the overall mass loss of pomegranate fruit (cv. Wonderful) at 278.15 K and 77%, 82% and 93% RH, respectively[8]. The authors observed that the contribution of net transpiration rate increased with decreasing storage temperature, especially at 77% and 82% RH. Water follows morphological pathways from the inside of the product, across the surface openings; the stomata, lenticels, bruise-damaged areas and cuticle to the surrounding, along a concentration gradient[25,26].
The rate of moisture loss is dependent on both the driving force and tissue properties. This process is described using Fick's first and second laws of diffusion[27]. According to Fick's first law, the rate at which a product loses moisture is directly proportional to the driving force under steady-state conditions[27]. The driving force responsible for water loss is centred on the differences in the proportion of moisture inside the product and that of the surrounding atmosphere. Therefore, driving force is defined using various parameters that describe the proportionality of moisture in a medium such as partial pressure of water vapour[6,28], water activity[29], chemical and water potential[2,23] or simply water concentration in case of passive diffusion[2]. In some studies, the driving force in terms of water potential difference was preferred compared to water concentration difference, because the diffusion phenomenon across the produce surface involves water in liquid and vapour states[26]. Knoche et al.[30] further report that water vapour may diffuse across the peel in either liquid or gaseous states. The driving force is majorly influenced by product temperature, environmental temperature and relative humidity[6]. Usually, at a particular product temperature, water vapour is forced to move from the intercellular spaces which have a high water vapour partial pressure (WVP) closer to saturation[31], to the outside air having a lower WVP.
Respiration
-
Harvested produce continues to live and the energy produced during respiration is used to support cellular biochemical processes[31]. Respiration utilises sugars and organic acids in the presence of oxygen to generate energy, produce carbon dioxide, and water and dissipated heat[32]. Figure 1 illustrates the concept of the respiration process inside a plant cell showing different mass and heat components involved. Respiration occurs majorly in the mitochondria of the produce cells where the major oxidation enzymes required for the process are found. In many studies, the dependence of respiration rate on oxygen consumption has been demonstrated numerically using Michaelis–Menten kinetics[20,33,34]. The respiration rate of fresh produce is often expressed in terms of oxygen consumption rate or carbon dioxide production rate. It is important to note that the carbon dioxide production rate is one of the indicators of the contribution of respiration in the weight loss of fresh produce. This is because the carbon dioxide gas released outside the produce during gaseous exchange, significantly contributes to product weight loss in the form of carbon loss[8]. The rate of carbon loss is directly proportional to respiration rate[2]. Furthermore, respiration facilitates and promotes water loss through the transpiration mechanism.
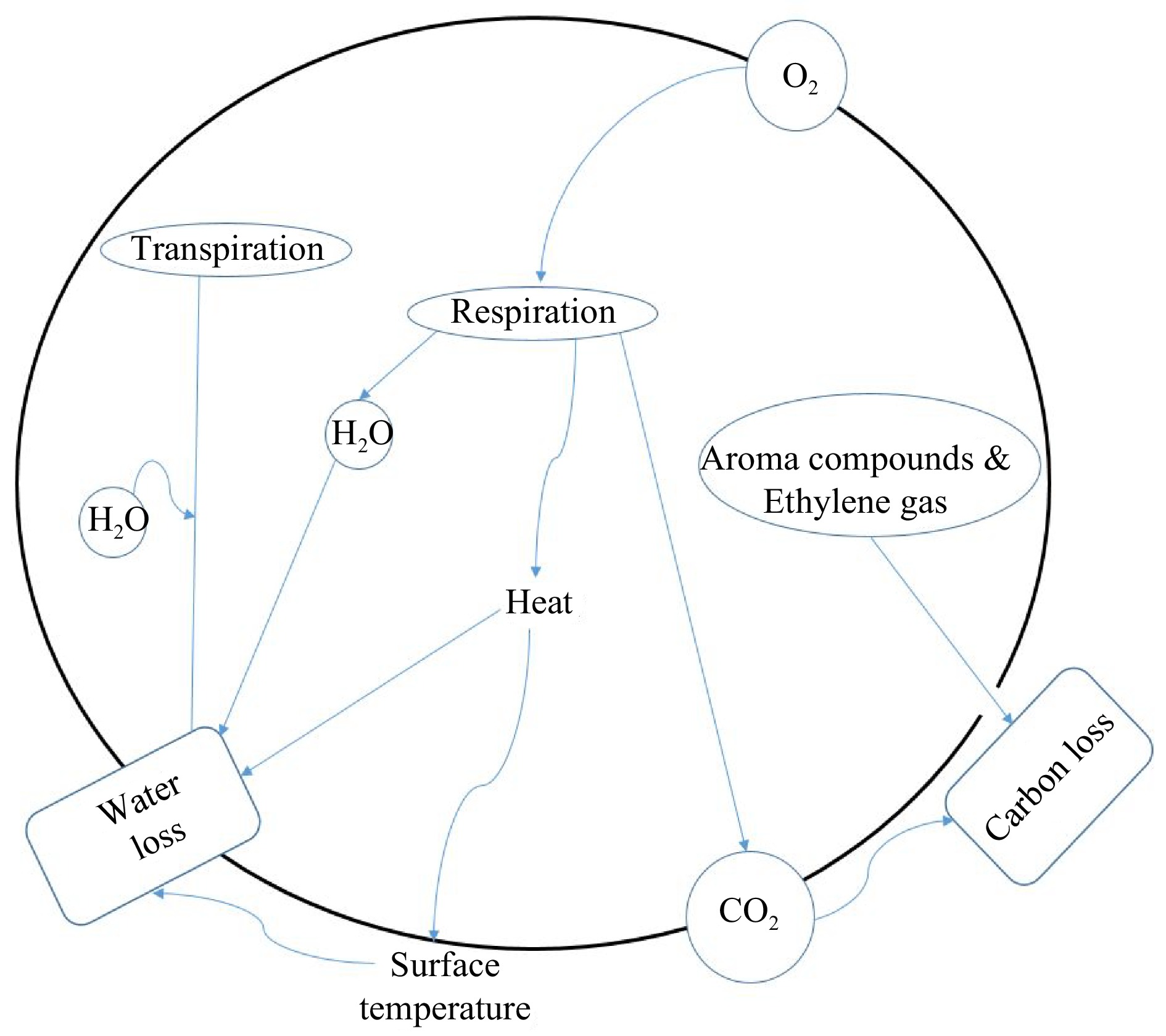
Figure 1.
The concept of the respiration process in a plant cell showing the different mass and heat components involved.
Respiration facilitates transpiration in two ways. Firstly, the water generated by substrate oxidation is partially or wholly lost as water vapour during transpiration. Xanthopoulos et al.[9] reported respiratory water loss of up to 39% in pear fruit stored at 293.15 K, 95% RH, with an average of 8%, 14% and 23% at 273.15, 283.15 and 293.15 K, respectively. Secondly, the heat that is produced from the respiration process facilitates transpiration in different ways. It is established that the energy produced inform of ATP is used to support cellular life processes and part is lost in the form of heat[35]. The resulting respiratory heat is used partly as sensible heat increasing product surface temperature[6,36]. This translates into increased water vapour pressure deficit (WVPD) or driving force between the product and its surrounding atmosphere resulting into increased rate of moisture loss[1]. As a result of respiratory heat dissipation, Bovi et al. reported 0.01, 0.07 and 0.12 K increase in surface temperature of strawberries stored at 277.15, 285.15 and 293.15 K, respectively, under saturated conditions of 100% RH. Furthermore, a residual transpiration rate of 0.002, 0.019 and 0.048 mg·kg−1·s−1 was observed in strawberries at the respective storage temperatures. This was attributed to the 0.01, 0.07 and 0.12 K increase in surface temperature at 277.15, 285.15 and 293.15 K, respectively, as a result of respiratory heat dissipation[11].
In addition, respiratory heat provides the necessary latent heat of vaporisation, resulting into moisture loss to the surrounding atmosphere[37,38]. For this reason, proper aeration within bulked and stacked produce is recommended as an industrial practice to promote faster cooling process and easy convective removal of dissipated heat during storage and transport. Lowering respiration rate, therefore reduces the rate of moisture loss[8,39,40]. The rate of a respiration process greatly depends on temperature of the product[8,40−42].
Amarante observed that the proportion contributed by respiration to total weight loss varied significantly among pear cultivars. The 'Comice' cultivar had the highest proportion of respiratory weight loss (4.25%), followed by Packharm's (3.86%), Bartlett (2.93%) and Bosc (2.37%) cultivars. These results were despite the fact that respiration rate was highest in 'Bartlett' pears and more similar among the other cultivars[12]. Furthermore, 'Bartlett' and 'Bosc' had higher carbon dioxide and oxygen permeance than other cultivars. However, because of the higher water permeance of the 'Bosc' and 'Bartlett' pears the proportion of respiratory weight loss was much lower than in other cultivars[43].
The contribution of respiration rate to overall product weight loss becomes more significant when produce is stored in high humidity environments (low driving force) minimising transpiration process and at high temperatures, increasing respiration[8,40,44]. Therefore, respiration rate should be put into consideration when evaluating weight loss of products in high humid environments such as inside MAP liners[2]. At saturated conditions of 100% RH where no transpiration is expected, Bovi et al. attributed the residual transpiration rate of 0.002 to 0.048 mg·kg−1·s−1 to the respiration heat dissipation for strawberries stored at 277.15, 285.15 and 293.15 K[11]. Respiration contributes about 7% to total weight loss for apples stored at 273.15 K and 90% RH[1]. Furthermore, respiration rate can contribute 9%–26% of total dry weight loss for pomegranate (cv. Wonderful) stored for 10 weeks at temperatures between 273.15–303.15 K[45].
Other weight loss mechanisms
-
Studies carried out on strawberries have reported the inability of temperature and RH or WVPD to comprehensively account for overall mass loss[11,46]. Besides transpiration and respiration, other possible mass flow components that contribute to the total produce weight loss result from mechanisms by which ethylene gas, volatile and aromatic organic compounds are lost, depending on the climacteric or non-climacteric nature of the produce[11−14]. The role of these other mechanisms is considered negligible in the weight loss of fresh produce, though their contribution is expected to increase under high humidity storage conditions[8,11,12].
-
The structures of products that are in the visible range of the naked eye are considered macroscopic. At this level, fruit are made up of several layers of different tissues. A simple fruit consists of three regions: an endocarp region at the centre, mesocarp region and the outer most region, the exocarp. The exocarp is further differentiated into the inner layer known as the hypodermis and the outer layer, the epidermis. The latter is often overlayed with a non-cellular layer called the cuticle.
Water moves from the inside of the fruit towards the surface following a water concentration or potential gradient and fruit tissues resist water movement to varying degrees. Table 1 shows experimentally determined water transport properties across different fruit tissues. It is observed that the inner tissues such has the mesocarp or cortex have a water diffusivity of two to three magnitudes higher than that in outer tissues of the cuticle (cutin and wax). The cellular layers of the peel epidermis and hypodermis are easily permeated with water owing to their structural composition that involves un-modified cellulose[31]. Given that the epidermis and hypodermis offer less resistance to water migration, the cuticle as the outer most non-cellular layer of the peel commonly serves as the last and most important barrier against excessive moisture loss[30,47]. The cuticle consists of the cutin layer (composed of cellulose, proteins, phenolic compounds, and acids) and a lining of epicuticular wax layer. It is the waxy part of the cuticle that is responsible for the big resistance against transpiration, majorly due to the hydrocarbons, long chain alcohols and aldehydes of the wax[23,48]. The wax component contributes 97.9% of the cuticular diffusive resistance against water conductance as compared to the cutin matrix (2.1%)[30]. The cuticle layer often covers other openings (stomata and lenticels) on the epidermal layer and commonly extends through the epidermal cells in some parts[49,50]. This therefore minimises water loss across the surface opening. Most water conductance was observed across the cuticular membrane (85.7%) as compared to the stomatal route (14.3%) in the cheek region of sweet cherry (cv. Sam)[30].
Table 1. Moisture diffusivity across fruit tissues.
Fruit Conditions of determination Part of fruit Diffusion coefficient (m2·s−1) Ref. Pear
(cv. Conference)Mesocarp (flesh) 1.520E-11 to 1.730E-11 [51] Cuticle 1.100E-13 to 1.200E-13 Pear
(cv. Conference)273.15 K Inner cortex tissue 1.230E-11 [18] 293.15 K 4.359E-11 273.15 K Outer cortex tissue 5.300E-13 293.15 K 1.050E-12 273.15 K Cuticle 5.500E-14 293.15 K 1.280E-13 Apple
(cv. Jonagold)273.15 K,
92% RHTissue 1.120E-11 [26] Cutin 6.420E-14 Wax 2.100E-15 Cuticle 8.740E-15 Apple
(cv. Estar)273.15 K,
92% RHTissue 4.330E-12 Cutin 7.160E-14 Wax 3.030E-14 Cuticle 5.080E-14 Apple
(cv. Jonagored)273.15 K,
92% RHMesocarp tissue 1.380E-11 Cutin 4.030E-14 Wax 1.920E-15 Cuticle 9.100E-15 Apple
(cv. Jonagold)Flesh 1.030E-10 [52] Skin 1.320E-13 Micro-structure
Water pathways inside the fruit
-
The majority of cells in fresh produce tissues are of the parenchyma type[53], possessing thin cell walls and relatively large vacuoles. Water is confined in three regions of the cell. The majority of the water known as intra-cellular water is found within the confines of cell membrane, while as cell wall water is locked up in the cell wall, and intercellular water is found within the intercellular space network[15]. Depending on transportability, intercellular, intracellular and cell wall water can be termed as free, loosely bound and strongly bound water[16]. This implies that free water is easily lost to the environment, followed by loosely bound and strongly bound water, respectively. Different pathways have been proposed to describe water movement at cellular level.
Through the Apoplastic pathway, water moves from cell to cell through the interconnected cell wall network. Alternatively, water moves through the continuous cytoplasmic system (Symplastic pathway) from cell to cell across small openings the Plasmodesmata find in the cell walls of adjacent cells. In the transmembrane pathway, water sequentially enters and exits one cell into another across the cell membrane and can cross into the intercellular space[17]. In the Intercellular pathway, water moves through the network of intercellular spaces, which is also the major route supporting gaseous exchange between the product and its surroundings. Fresh products consist of loosely bound cells with considerable intercellular spaces, which are interconnected, leading to numerous openings on the product surface. Moisture therefore, diffuses from the cells (regions of high water concentration) into the intercellular spaces (regions of low water concentration) until a near saturation point is reached[25,26]. Furthermore, water diffuses through the intercellular spaces along a concentration gradient from the inner tissues (with high water content) to outer surfaces (with lower moisture content)[2]. Water movement along this route occurs both in liquid and vapour states[23], but predominantly in liquid state[31], given the minor difference in water vapour deficit between cells of the inside tissues and outside surfaces[54]. This is the most widely adopted pathway to explain transpiration in harvested products[2,23,26].
Water movement to the outside
-
At the product surface, water loss is aided and influenced by the existing numerous openings such as stomata, lenticels and micro-cracks and other structures like trichomes. Stomatal density varies among produce, cultivars, and surface position on the product. Higher stomatal density was observed on the ventral suture and stylar end than on the cheek regions of sweet cherry (cv. Sam)[30]. Stomata tend to lose their functionality in fully developed and harvested produce, because some of the stomata get partially or fully clogged with wax and other materials[30], greatly minimising their role in water transport. However, lenticels are the more likely pores responsible for transpiration and gaseous exchange in harvested mature fruit and vegetables, as compared to stomata[26]. Lenticels originate from dysfunctional stomata, especially due to skin expansions and when the guard cells lose their ability to control opening and closure during growth and development[55]. Just like stomata, some lenticels are clogged with wax or other materials such as suberised periderm, thus providing a barrier against water loss[23]. As a result the number of open stomata becomes crucial in water loss studies, as observed in apple fruit (cv. Jonagold and Elstar) with an average 42% ratio of open to closed lenticels[23,29]. In pomegranate fruit (cv. Wonderful), a higher count of lenticels and larger lenticel size were observed at the calyx-end and equatorial-region than at the stem-end of the fruit[50]. As a result, a noticeable water loss trend was evident with respect to region on the fruit, the calyx-end being more susceptible compared to the stem-end.
Another important outlet of water loss in harvested fruit are the numerous surface micro-cracks. These cracks provide openings for loss of excessive moisture and may facilitate pathogen invasion leading to fruit decay and rotting[50]. In European plums, surface cracks and shrivelling have been identified to co-exist in the regions of high moisture loss occurrences, around the pedicel[56]. Surface cracks appear as breakages in the cuticular layer, when the rate at which the product is expanding during development outweighs the rate at which the cuticle layer is deposited to cover the product[56]. Therefore, this occurrence is more common in matured or overly matured fruit. Furthermore, high humid conditions result in water redistribution from leaves and branches into the fruit, provoking surface expansion and cracking[57].
-
From a broader perspective, it is not practical to measure all water transport parameters on a very large scale such as at the factory level or fruit storage facility. However, through modelling, mass transport can be simulated, studied, and controlled on a large scale. Moisture loss is the largest contributor to weight loss in fresh produce[8]. Modelling of water transport at different levels of scale including, cellular (micro-structure scale) level, tissue (mesoscale) level, macro level (whole fruit scale) and multiscale level (bulked and packed fruit) is promoted to facilitate further understanding of the mechanisms of weight loss[58]. Table 2 shows water transport models in fresh fruit applied at microscale, mesoscale, macroscale and multiscale.
Table 2. Water transport models in fresh fruit applied at microscale, mesoscale, macroscale and multiscale.
Model scale Fresh produce Structural/geometrical details Details of water transport model Ref. Nanoscale Artificial plant cell walls The objective was to study the effect of cell wall composition and temperature on the structure, desorption isotherms and water conductivity of artificial cell walls. [59] Microscale Pears (cv. Conference) 2D geometric model of cortex tissue, composed of cells of random sizes and shapes, cell walls and intercellular spaces. A steady state model applied,
Modelling of water transport in the intercellular space, the cell wall network and cytoplasm was done using diffusion laws and irreversible thermodynamics.[58] Microscale Pear (cv. Conference) cortex tissue intercellular space, cell wall network and cytoplasm A 2D geometrical model was obtained with a virtual fruit tissue generator, based on cell growth modelling. To account for the microstructure, a microscopic layout was introduced into the modelling as the computational geometry of the model. Water transport was described using a coupled approach incorporating the microscale water transport model and the cell mechanics model that predicts cell and tissue deformation resulting from hydrostatic stress caused by moisture loss. [60] Microscale & Mesoscale Apple (cv. Jonagold and Elstar) cuticle: Tissue, cutin and wax Water transport is modelled at a mesoscale (tissue) level by considering moisture loss across the cuticle.
However, a more detailed microscopic approach was applied to account for the microstructural features of surface cracks, open and closed lenticels.
In the geometrical basis of the moisture diffusion model, lenticel and crack structures, total crack area, and effect of wax smoothing were incorporated.The actual diffusion properties of the cuticle, cutin and wax were derived from apparent diffusion properties determined experimentally using gravimetric procedures. [23] Mesoscale Apple fruit tissues (cv. Elstar, Jonagold and Jonagored). A mesoscale geometry of apple tissue cylinder was constructed to represent fruit tissue, cuticle and cutin and wax layer. Water transport across fruit tissue, cutin and surface wax layer was simulated.
Diffusion coefficients of apple tissue and cuticle were experimentally determined using apple tissue cylinders with intact cuticle, without cuticle or without wax.[26] Mesoscale Apple fruit (cv. Jonagold): Cylindrical apple tissue A coupled mass transfer and mechanics model was used to describe water transport and associated deformation of apple tissue during dehydration.
The model was one-dimensional.[61] Mesoscale Conference pears tissues (cuticle, inner and outer cortex) Water transport in the different fruit tissues was described using sorption isotherm experimental data, fitted with Ferro Fontan model. [62] Mesoscale Conference pears tissues (cuticle, inner and outer cortex) Water transport in fruit tissues was described based on effective diffusivity of water. Modelling was done using Fick's first and second laws of diffusion on the cuticle and cortex tissues, respectively. A chemical potential gradient was employed as the driving force. [18] Mesoscale and Macroscale Pears (cv. Conference): cuticle, inner and outer cortex A computer vision-based modelling system was used. Eight digital images of the fruit taken from different directions. A 3D shape of the whole fruit was reconstructed from contours extracted from the images. The diffusion model was based on Fick's second law, to simulate water transport in whole fruit at shelf (293.15 K, 75% RH) and cold storage (274.15 K, 60% RH) conditions.
Different pear tissues with varying diffusion properties, were used to describe water transport at a mesoscale level.[63] Macroscale Apple (cv. Elstar and Jonagold) A wedge-shaped geometrical model was used to predict moisture loss over a whole apple during 6 months of controlled atmosphere storage. Actual diffusion coefficients of apple tissue, cutin, wax and cuticle were integrated with different geometric sub-models in order to predict moisture loss of whole fruit under specific storage conditions. [29] Macroscale Apple whole fruit
Macro-scaleMacroscale water transport model for the entire fruit A microscale model was used to compute the water transport properties of the apple skin. Then the water transport model for the entire fruit was computed from the water transport properties of the skin. [26,29] Multiscale (Combined microscale and macroscale) Apple tissue (cv. Jonagold) A 2D multiscale water transport and mechanical model was used to predict water loss and viscoelastic deformation.
The apparent parameters of the macroscale model were computed from a microscale model. At a microscopic level, water movement across tissue microstructures: cell wall network, cytoplasm and intercellular space were considered.[64] Nano and micro level
-
This level often considers the cell as the smallest unit of water transport in fresh produce. At the cellular level, water exists as free (intercellular), loosely bound (intracellular) and strongly bound (cell wall) water, depending on the ease of transportability[15,16]. As a result, transport models have been developed to account for water movement through cells and intercellular spaces[58]. Modelling of water transport at this level, appreciates the fact that there is a lot of heterogeneity in tissue structure, resulting from the complexity of different cellular structure and arrangement. This level allows for detailed structural consideration and obtaining of physical parameters rather than parameter estimation applied at larger scales of modelling[20]. The structural complexity at this level can be represented using geometrical models[58,65].
Given the complexity of cell structure, the micro-scale level can further be broken down to nano-scale level to give critical attention to details. At nano-level, water transport across cell walls has been successfully modelled[64]. The authors applied the unsteady-state diffusion model to describe water transport across the cell walls. Other researchers have coupled water transport models at this level with mechanical deformation models to describe the deformations such as shrinkage, resulting from plasmolysis (loss of turgidity) that can happen in a cell as a result of moisture loss and consequently loss of market quality[60,65]. The water transport properties obtained at this level can be further used in developing larger scale models of water transport and weight loss[65]. However, this approach requires largely increased computational time and power.
Meso-level
-
Water transport at this level is modelled on plant tissues such as the cortex tissue and cuticular layer of a fruit. Studies in this area have been done on apple and pear fruit, with moisture transport modelled using Fick's first and second diffusion laws[18,23,26,29,51]. Diffusivity or permeability is the mostly used parameters to describe water transport and moisture loss at this level, and can be deduced from collected experimental data obtained using permeation, sorption-desorption kinetics or moisture concentration techniques[18]. In the permeation method, diffusivity is obtained from the rate of moisture transfer across the tissue while in sorption-desorption methods, diffusivity is deduced from sorption-desorption kinetics. On the other hand, diffusivity can be calculated from moisture concentration resulting from diffusion across the axis of a cylindrical tissue, using the concentration-distance approach. The permeation and concentration-distance methods have been commonly applied on apple and pear tissues[18,26,51], while the desorption method has been applied on tissues of other fruit such as mango slices[66].
Macro-level
-
Weight loss of a whole intact fruit is commonly modelled based on transpiration process[3,9,10,67]. This is because transpiration is the major contributor to product overall weight loss as compared to respiration process[8]. Transpiration rate can be expressed using a gravimetric approach, in terms of weight loss of fresh produce[3,67]. The rate of transpiration is directly proportional to the driving force responsible for moisture loss and resistance against moisture loss, and is in line with Fick's first law of diffusion[3,28,67−69].
The inverse of the transpiration coefficient represents the resistance. The limitation of using transpiration coefficients to calculate transpiration rate (mass loss) is that they are dependent on the product type and operate within a range of experimental conditions[70]. Different results can be obtained even for the same product, due to differences in experimental methods applied[69] and the assumptions that are considered in calculating the transpiration coefficient[70].
Furthermore, water permeability has been calculated on whole intact fruit such as in 'Braeburn' apples[71], 'Bartlett', 'Beurre Bosc', 'Doyenne du Comice' and 'Packham's Triumph' pears[43], Japanese plum cultivars 'African Rose', 'Angeleno', 'Ruby Sun', 'Fortune' and 'Ruby Star'[72], 'Laetitia' and 'Songold' plums[73] based on Fick's first law of diffusion. However, the determination of water transport properties of the different tissues of the fruit is very important in facilitating detailed investigation of the spatial-temporal moisture distribution within the fruit.
Advances in the scale of modelling
-
Modelling of water transport in fresh fruit has been carried out in two broad approaches: the microscopic approach and the macroscopic continuum approach[58]. The later considers the specimen (material under investigation) as a generalised homogenous entity. As a result, it is a simple and easy way of describing water transport in fruit tissues because it does not necessitate modelling of the microstructures such as pores space, cell membrane and cell wall[18,26,63]. In this case, the whole fruit is assumed to be a homogeneous system with general effective properties[74−76]. However, detailed insights into water transport at the micro-scale is lost. This is because it employs parameters that are more apparent compared to physical parameters that are attainable at microscopic levels[20].
On the other hand, the microscopic approach considers structural complexity of the material, recognizing the heterogeneity in transport properties existing between compartments. However, a detailed representative geometric construction is relevant. Geometric models of plant tissues have been constructed through imaging of the microstructure using various techniques such as x-ray computed technology[77] and microscopy imaging technology[23]. Alternatively, Fanta et al.[58,60] used a virtual fruit tissue generation algorithm to generate 2D tissue structure composed of randomly sized and shaped cells, cell walls and intercellular spaces. The structure was then compared with fruit tissue micrographs. A change in cell density and volume due to shrinkage was accounted for. The authors then modelled water transport of the intercellular space, the cell wall network and cytoplasm by applying diffusion laws and irreversible thermodynamics according to Nobel[27].
A multiscale approach is one of the recent advances being applied in water transport modelling. This approach has applications in biological sciences where it has been used in a 3D modelling of gas exchange in fruit[64,78]. A multiscale model is a hierarchy of models describing material properties including water transport properties at different spatial scales, in such a way that the underlying sub-models are interconnected[20]. The authors carried out a detailed review on multiscale modelling. Multiscale modelling facilitates computational analysis in solving complex industrial problems. At this level, we appreciate that foods are hierarchically structured and have features that extend from molecular scale level to the food plant scale[20]. The different spatial scales involved include, nano level (e.g. Aquaporin and cell wall), microscale level (e.g. individual plant cell), mesoscale level (e.g. cortex tissue of an apple fruit) and macroscale level (e.g. whole fruit having different components)[21] as illustrated in Fig. 2. Multiscale combines the details obtained through microscale and mesoscale modelling and applies them at a macroscale level. The biggest limitation of this level of modelling is large computational time and power required. As a result, averaging procedures are applied to reduce on structural details and obtain more apparent parameter estimates[20].
Transpiration modelling
Measurement
-
Transpiration is often calculated as the rate of moisture loss in horticultural products, with moisture loss being commonly expressed as a change in product mass[8,67,70]. This is because of the assumption that the change in product mass is entirely due to moisture loss from the fruit during storage. In this case, transpiration rate (TR) can be calculated per unit of initial product mass (
$ {TR}_{m} $ $ {TR}_{A} $ $ {T R}_{m}=\dfrac{{m}_{i}-{m}_{t}}{t\;\times\; {m}_{i}}\;\times\; {10}^{6} $ (1) $ {T R}_{A}=\dfrac{{m}_{i}-{m}_{t}}{t\;\times\; A}\;\times\; {10}^{6} $ (2) Where
$ {m}_{i} $ $ {m}_{t} $ $ t $ $ A $ Modelling
-
Despite a multitude of factors influencing moisture loss in fresh fruits and vegetables, transpiration can in basic terms be envisaged as result of a driving force-resistance interaction, with the following mathematical expression (Eqn (3))[36,68,69]:
$ {T R}_{m}={K}_{i}\left({P}_{s}-{P}_{\infty }\right) $ (3) where
$ {K}_{i} $ $ {P}_{s} $ $ {P}_{\infty } $ $ \left(VPD={P}_{s}-{P}_{\infty }\right) $ Modifications of Eqn (3) have been done portraying that transpiration rate and the mass transfer coefficient exponentially depend on the storage temperature, as in Eqns (4)[67] and (5)[79]
$ {T R}_{A}={K}_{i}\;\times \;\rho \left({a}_{{w}_{i}}-{a}_{w}\right)\;\times\; \left(1 -{e}^{-\alpha T}\right) $ (4) $ {T R}_{m}={K}_{i}\left({a}_{{w}_{i}}-{a}_{w}\right)\;\times\; \left(1 -{e}^{-\alpha T}\right) $ (5) where,
$ \rho $ $ \alpha $ $ T $ $ {a}_{{w}_{i}} $ $ {a}_{w} $ $ {a}_{{w}_{i}}-{a}_{w} $ $ T R={T R'_{0}}{e}^{\frac{{-E'}}{{R}_{g}T}}=a{e}^{\frac{b\,\times\, RH}{100}}{e}^{\frac{-{E'}}{{R}_{g}T}} $ (6) $ T R={T R''_{0}}{e}^{\frac{{-E''}}{{R}_{g}T}\,\times\, \frac{RH}{100}}={a'}{e}^{\frac{{b'}\,\times\; RH}{100}}{e}^{\frac{-{E''}}{{R}_{g}T}\,\times\, \frac{RH}{100}} $ (7) where,
$ {R}_{g} $ $ {TR'_{0}} $ $ {TR''_{0}} $ $ {E'} $ $ {E''}$ $ a $ $ b $ $ {a'} $ $ {b'} $ Studies have examined the relationship between transpiration rate and the driving force for several fresh produce, and have revealed a deviation between the linear model predictions (Eqn (3)) and the experimental data[8,11,46]. Deviations were evident under very high relative humidity environments (saturation conditions). Theoretically, transpiration should be zero when the driving force is zero, however, a mass loss rate of TRA = 0.029 − 0.274 mg·m−2·s−1 (TRm = 0.002 − 0.018 mg·kg−1·s−1) was noticed in pomegranate fruit[8]. This shows that there may be additional mass flow components such as carbon loss and respiratory heat generation resulting from product respiration, which influence transpiration rate and contribute to the overall mass loss particularly in extremely high relative humidity and low temperature situations. Therefore, other transpiration models have been suggested, accounting for the contribution of respirational components in the water loss of fresh produce, most especially under high humidity environments and packaging applications.
Equation (8) presents a heat-mass balance transpiration model that expresses the transpiration rate as a function of respiratory heat, and the temperature difference between the product and its environment[37].
$ {T R}_{A}=\dfrac{Q{m}_{i}+h\left(T-{T}_{p}\right)}{\lambda } $ (8) where,
$ Q $ $ h $ $ T $ $ {T}_{p} $ $ \lambda $ Furthermore, a general mathematical model (Eqn (9)) was created and expressed as a function of storage temperature, relative humidity, and emitted respiratory heat from the product kept under water saturation conditions, to forecast transpiration rate[44]:
$ T R={K}_{i}\left({a}_{{w}_{i}}-{a}_{w}\right)\left(1 -{e}^{-\alpha T}\right)+8.6{RR}_{{CO}_{2,ref}}{e}^{\frac{-_{{E}_{a}}}{{R}_{g}}\left[\frac{1}{\left(T+273\right)}-\frac{1}{\left({T}_{ref}+273\right)}\right]} $ (9) where
$ {E}_{a} $ $ {R}_{g} $ $ {T}_{ref} $ $ {RR}_{{CO}_{2,ref}} $ $ {T}_{ref} $ Unlike unpackaged fresh produce, modelling transpiration of products under packaging systems requires critical understanding and consideration of the interactions between the barrier properties of packaging material (gas and moisture permeability) and the evaporation of the product surface due to respiratory heat (Song et al.[38]). Because of their barrier properties, loose modified atmosphere packaging films promote moisture build up around the product, creating conditions of vapour saturation and stagnated flow of air, which could lead to moisture condensation inside the packaging.
Models of mass transfer through perforated packaging have been reported in literature and have been reviewed[70]. The impact of film perforations on water flux has been modelled and investigated[82] and similarly Mahajan et al.[83] modelled the WVTR of packaging film as a function of storage temperature and perforation dimensions (Eqn (10)), where
$ D $ $ L $ $ WVT R=2.28 \times {D}^{1.72}\,\times\, {L}^{-0.72}\,\times \,{e}^{\frac{-12.62}{{R}_{g}T}} $ (10) The role of imaging technologies
-
One of the ways of improving the accuracy and robustness of water transport models lies in capturing as much detail as possible rather than generalising and lumping of important parameters. This is because fruit are highly heterogeneous and complex in structure. Imaging technologies have made it possible to easily visualise the complex structures and subsequently enable the construction of geometric models required for in depth simulation studies.
Microscopy technology has been widely exploited to obtain details of fruit surface structures. Common microscopes applied in such studies include confocal laser scanning miscopy (CLSM), scanning electron microscopy (SEM), environmental scanning electron microscope (ESEM), light microscopy (LM) and transmission electron microscopy (TEM). The combination of two or more of the above microscopy techniques has been applied to examine and characterise the morphology and structure of fruit skin and surface structures such as wax, micro-cracks and stomata in plums[73,84] and apples[71,85−88]. A combination of CLSM, ESEM and LM have been used to obtain images of fruit surface layers and structures making in it possible to obtain their dimensions (depth, length and width) then the images were used to construct geometric models in the finite element methods[23]. Despite the very high image resolution obtainable by some of these microscopes such as in SEM, the biggest limitation of these microscopy techniques is that they majorly produce data in two dimensional (2D) images which is quite limiting in detail compared to three dimensional (3D) images.
Technologies such as X-ray computed tomography (X-ray CT) and magnetic resonance imaging (MRI) with the capability of producing 2D images that can easily be reconstructed into 3D images are being sought after. X-ray micro-computed tomography (X-ray μCT) has diverse applications in the food industry[89]. This imaging technique creates contrast among fruit structures based on their ability to attenuate X-rays owing to differences in mass densities of the fruit material, with pore space visualized as regions with low intensities. Multiple virtual 2D projection images of slices through the study sample are acquired, followed by reconstruction of consecutive virtual slices to obtain 3D images. The 3D images provide information on pore space distribution making it relevant in simulation studies on heat and mass transport[77]. Mendoza et al.[90] used X-ray µCT to visualize and characterize the 3D microstructure and pore space network of apple tissue. Herremans et al.[91] characterized the 3D microstructure of apple (cvs. Jonagold, Kanzi and Braeburn) and pear (cv. Conference) parenchyma tissue, considering individual cells and intercellular spaces. Cantre et al.[92] investigated changes in the 3D microstructure of mango (cv. Carabao) during ripening.
MRI has been embraced as an important non-invasive technique for visualising and monitoring of water transport processes in material science and the food industry. An external magnetic field is applied on the water-containing object, causing the protons (hydrogen nuclei) to become polarized and aligned parallel with the external magnetic field, establishing an equilibrium. Another magnetic field in the form of a radio frequency pulse radiation is applied for a specific time perpendicular to the main magnetic field. This disturbs the previous alignment, and the protons produce a rotating magnetic field which is detected as a signal. The signal undergoes Fourier transformation to produce images which are reconstructed into 3D volume images[93,94]. The intensity of the MRI signal is proportional to the number of protons (hydrogen nuclei) in the sample and is often equated to moisture content because the protons are mainly from the water within the sample. Therefore, MRI has been used to acquire temporally and spatially resolved moisture profiles of materials[95]. For example, MRI has been used to detect water core in apples[96], estimate parameters of moisture transport in apple tissues[52], water transfer in meat[97] and measurement of bound and free water distribution in wood during water uptake and drying[98].
-
It is simple to weigh fruit and determine their mass profile with time. However, the underlying mechanism of water transport phenomenon and water loss are not obvious. This review portrays the complexity of water loss in fresh fruit which involves the combination of physiological and morphological mechanisms. Transpiration (moisture loss) is the major process by which fresh produce lose saleable weight during postharvest handling. Respiration process has been identified as contributor towards physiological weight loss especially at high relative humidity conditions.
The review details the path of water from the inside of the fruit to the outside, giving specific attention to this phenomenon on the micro and macro scale level. The review acknowledges that fruit are hierarchically structured and have features that extend from the molecular scale level to the food plant scale[20]. Therefore moisture transport in fresh fruit can be modelled at different levels of spatial scales including, nano level (e.g. Aquaporin and cell wall), microscale level (e.g. individual plant cell), mesoscale level (e.g. cortex tissue of an apple fruit) and macroscale level (e.g. whole fruit having different components)[21]. However, a multiscale model is recommended which involves a hierarchy of models describing material properties including water transport properties at different spatial scales, in such a way that the underlying sub-models are interconnected.
-
The authors confirm contribution to the paper as follows: study conception and design: Opara UL, Ambaw A; data collection: Lufu R, Ambaw A, Opara UL; analysis and interpretation of results: Lufu R, Ambaw A, Opara UL; draft manuscript preparation: Lufu R, Ambaw A, Opara UL. All authors reviewed the results and approved the final version of the manuscript.
-
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
This work is based on the research supported in part by the National Research Foundation of South Africa (Grant Number: 64813). The opinions, findings and conclusions or recommendations expressed are those of the author(s) alone, and the NRF accepts no liability whatsoever in this regard. Research reported in this publication was supported in part by the Foundation for Food and Agriculture Research under award number – Grant ID: DFs-18-0000000008.
-
The authors declare that they have no conflict of interest. The mention of commercial products in the article is to provide complete description as presented by the cited reference and does not represent endorsement by the authors or their respective institutions.
- Copyright: © 2024 by the author(s). Published by Maximum Academic Press, Fayetteville, GA. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
-
About this article
Cite this article
Lufu R, Ambaw A, Opara UL. 2024. Mechanisms and modelling approaches to weight loss in fresh fruit: a review. Technology in Horticulture 4: e006 doi: 10.48130/tihort-0024-0003
Mechanisms and modelling approaches to weight loss in fresh fruit: a review
- Received: 04 December 2023
- Revised: 29 January 2024
- Accepted: 13 February 2024
- Published online: 15 March 2024
Abstract: The symptoms of fruit weight loss are common, including but not limited to shrivelling, changes in product colour, textural properties, total soluble solids, product flavour and saleable weight. However, fruit weight loss is a complex process involving the interaction of product morphology, physiology, and environmental influence. Fruit is hierarchically structured and has features that extend from the molecular scale level to the food plant scale and yet water transport occurs at different spatial scales including nanoscale, microscale, mesoscale and macroscale. Therefore, the modelling of water loss in fresh fruit has been done using micro, macro and multiscale approaches. This review aims to provide a detailed scientific understanding of the interaction between the mechanisms of weight loss and the water loss modelling approach in fresh fruit.
-
Key words:
- Water transport /
- Transpiration /
- Respiration /
- Multiscale /
- Fruit structure /
- Imaging technology /
- Postharvest /
- Fruit qaulity