-
Forecasting of airline passenger volume between pairs of cities is important to airport operators. The predicted volume can be used to guide and support the adjustment strategies of flights and airlines, thereby significantly enhancing the assurance of transportation safety. In stark contrast to the road transportation system, the latter confronts multifaceted challenges stemming from variable road conditions, unpredictable driver behavior, and disparities in vehicle performance[1]. These uncertainties collectively elevate the safety risk in road transportation. Conversely, the aviation transportation system exemplifies a heightened level of flight safety, attributable to its stringent safety management, cutting-edge technological equipment, and precise weather forecasting. Notably, the precision of passenger flow prediction is indispensable for ensuring the smooth and safe operation of flights in aviation transportation. Through accurate passenger flow forecasts, airlines can meticulously arrange flight schedules, mitigate the risk of flight overloads or resource misallocation, and minimize potential safety hazards during flight operations. Consequently, forecasting passenger volume enables airport operators to foresee potential peak hours and passenger flow patterns, facilitating proactive preparations for various safety assurance measures. Furthermore, precise aviation passenger flow forecasting not only safeguards transportation safety but also provides invaluable support for the measurement and management of carbon emissions within the aviation transportation system[2]. It is therefore important to identify the key factors and develop a proper model to predict airline passenger volume accurately.
Airline passenger volume refers to the volume of the specific flight path of an aircraft, which includes the given direction, starting and ending points, and stopping points. Air passenger volume is always calculated as the total airline passenger volume at one airport. Though air passenger volume is a common phenomenon, research on airline passenger volume is limited. Traditional methods used in these studies can be generally classified into two categories: time series models[3,4] and multivariate regression analysis[5,6]. These methods are available for air transport forecasting merely in terms of form, requiring refinement according to local characteristics when applied to practice[7]. Researchers[8,9] used algorithms based on the Markov chain or the improved Markov chain to predict aviation market demand. Pan et al.[10] developed an advanced snow-water equivalent retrieval algorithm based on the Markov Chain Monte Carlo method. However, these are essentially time series models that highlights the time series and does not consider the influence of external factors. Advanced forecast methods such as neural networks[11] and support vector machines (SVM)[12,13] have been applied to volume prediction because of their strong nonlinear fitting ability and flexibility. In the context of air passenger volume forecasting, a novel approach known as the nonlinear vector auto-regression neural network (NVARNN) has been introduced to address the complexities and challenges associated with predicting air passenger flows[14]. Hu[15] introduced a combination method based on grey prediction that outperformed other competitors considered in air passenger volume forecasting. Wu et al.[16] introduced a prediction model based on a two-phase learning framework, where various predictors are utilized in the first phase to cope with the forecasting task. This approach aims to improve the accuracy of predicting air passenger traffic flow. Additionally, Tan et al.[17] focused on improving synchronization between the high-speed railway and aviation services, highlighting the importance of coordinating timetables to meet intermodality traffic needs. The literature reviewed highlights the significance of the two-phase learning model in forecasting air passenger traffic flow. Researchers[18] used the time series model to predict the air cargo throughput and proved the accuracy of the 'optimal' regression equation is higher than that of the single factor time model. However, the disadvantage of neural networks is their 'black box' nature, meaning that it is not clear how and why the neural networks came up with a certain output. The SVM algorithm is difficult to implement when the size of the training sample is large, and solving the multi-classification problem remains difficult.
The panel data, which has a two-dimensional structure (i.e., cross-sectional vs time series), is a common dataset in economics. Cross-sectional data are the observations collected on several individuals/units at one point in time; time-series data are observations collected on one individual/unit over several time periods. Panel data are repeated cross-sectional observations over time; in essence, there will be space as well as time dimensions. The panel data model's structure can be well matched with air transport characteristics including noteworthy section characteristics and time trends. Hence, a prediction method based on the panel data model takes the external environment factors and the growing trends of each city-pairs into account.
This paper is organized in the following manner. First, potential factors impacting airline passenger volume are discussed, providing an overview of previous relevant research. After that, a description of the data source is given, followed by processes of determining major factors. Then the modeling process and model validation are shown. Finally, a case study and conclusions are presented.
-
Airline passenger volume is affected by many factors, and various studies have focused on determinants of air travel. Factors analyzed in previous studies can generally be classified into two categories: Geo-economic factors and service-related factors[19].
Geo-economic factors
-
Geo-economic factors that are often taken into account include population size, gross domestic product (GDP) or GDP per capita, tourism, and consumption capacity. A previous research studies[20] showed that population, GDP, and per capita GDP greatly impacted airline passenger traffic. In general, the GDP, population, and per capita GDP growth, along with the development of the social economy, stimulate the increase of airline passenger volume. Nguyen et al.[21] observed that a higher economic policy uncertainty leads to more departures and more total expenditures but less expenditure per tourist in low- and lower-middle-income economies, suggesting that economic factors play a role in air travel demand in these countries. Lee et al.[22] demonstrated the negative impact of geopolitical risks on international tourism demand, exacerbated by pandemic outbreaks.
Adedoyin et al.[23] studied the relationship between energy consumption, tourism, economic policy uncertainty, and environmental degradation, highlighting the role of uncertainties in driving ecological footprint. Bekun et al.[24] proposed a policy framework for sustainable development in the Next-5 largest economies, emphasizing the importance of energy consumption and key macroeconomic indicators. The research[25] utilized fixed effects models and a three-step error correction mechanism to analyze the factors influencing air transport demand in the region. Wang[26] found that residents' consumption capacity had a great effect on the way and frequency of travel, and the tolerance and sensitivity to price as well as the requirements on service quality were also affected. The researchers[27,28] discovered that tourism and air transport are closely related, and the development of tertiary industry, represented by tourism, greatly encourages air traffic growth. Distance is another factor that impacts air transportation; people traveling long distances are inclined to travel by air[26].
Service-related factors
-
Service-related factors mainly include ticket prices and the influence of railway transportation and highway transportation. Zou[29] found that railway and highway transportation impact airline passenger volume. Different transportation modes have different technical and economic characteristics, and their advantages differ from others as well. Fast-growing highway and railway transportation greatly influences air transportation. There are alternative or complementary relationships between the two modes of transportation. On the one hand, when airline passenger volume is diverted, airline passenger volume is reduced. On the other hand, multimodal transport relations may improve airline passenger volume.
Therefore, potential factors analyzed above include population, GDP, per capita GDP, residents' consumption capacity, the proportion of tertiary industry, highway, and railway passenger volume, and distance between city pairs. Factors such as population, GDP, per capita GDP, residents' consumption capacity, and the proportion of tertiary industry stimulates airline passenger volume when other factors such as highway and railway passenger volume remains unknown.
-
Table 1 provides a summary of the data used in the research. Population, GDP, and per capita GDP always refer to a measure of market potential related to the departure city. The residents' consumption capacity can be reflected in total retail sales of consumer goods. For a departure city, it embodies people's standard of living, and people are more likely to travel if the standard of living improves. For an arrival city, it reflects the total retail sales of both residents and tourists. Hence, the residents' consumption capacity is better reflected by the total retail sales of consumer goods in both departure and arrival cities. Tourism traffic is particularly attracted by one of the endpoints being an important tourism area[6], which indicates that the proportion of tertiary industry data is better collected from the arrival city. The linear distance between two cities was used as distance data. Note that, for railway and highway passenger volume, due to limited data availability, the product of the total passenger volume of the departure city and arrival city was used rather than the passenger volume on one route.
Table 1. Summary of data used.
Data name Symbol Airline passenger volume Vol Geo-economic factors Population Pop GDP GDP Per capita GDP PGDP Total retail sales of consumer goods of departure city DT Total retail sales of consumer goods of arrival city AT Proportion of tertiary industry PT Distance Dist Service-related factors Railway passenger traffic volume R Highway passenger traffic volume H Airline passenger volume data was extracted from the China Transport Statistical Yearbook (2003−2012), including 13 airlines between Beijing, Shanghai, Xiamen, Shenzhen, Guangzhou, Chongqing. Other data was collected from the Statistical Yearbooks of these cities. A total of 120 sets of airline data (excluding data from Chongqing to Shanghai is not included) were used to estimate the model and the 10 sets of airline data from Chongqing to Shanghai was used to verify the model. Table 2 provides summary statistics of the data used in this paper.
Table 2. Descriptive statistics of data.
Data symbol Units Mean Median Maximum Minimum Std. dev. Vol Ten thousand 1.749 × 106 1.341 × 106 6.800 × 106 2.239 × 105 1.390 × 106 Pop Ten thousand 1,448.009 1,638.500 2,945.000 220.285 831.751 GDP Hundred million 9,938.198 9,192.937 20,181.720 2,555.720 466.054 PGDP One hundred million yuan per ten
thousand people12.620 6.742 51.212 0.912 13.120 DT Hundred million 3,902.157 3,335.250 8,123.500 934.671 1,939.569 AT Hundred million 2,145.732 1,680.000 7,840.400 207.472 1,805.989 PT % 49.871 49.400 63.580 40.500 5.465 Dist Kilometer 1,201.950 1,213.250 1,945.320 464.550 629.753 R Ten thousand × ten thousand 1.847 × 107 1.009 × 107 1.100 × 108 3.013 × 105 2.170 × 107 H Ten thousand × ten thousand 3.194 × 109 4.521 × 108 2.731 × 1010 6.824 × 106 6.184 × 109 Principal components analysis
-
The PCA was performed using MATLAB to identify the determinant factors among those mentioned earlier. The characteristic values (eigenvalues) of each principal component's covariance matrix and their respective contribution rates are calculated (see Table 3). Principal components 1 to 4 have contributed more than 95% of the total variance, so principal components 5 to 9 can be omitted.
Table 3. Eigenvalue of variance and contribution rate.
Principal component (PC) Eigenvalue Contribution rate Accumulative contribution rate PC 1 5.982 58.93% 58.93% PC 2 2.033 20.03% 78.96% PC 3 1.473 14.51% 93.47% PC 4 0.444 4.38% 97.85% PC 5 0.163 1.60% 99.45% PC 6 0.047 0.46% 99.92% PC 7 0.006 0.05% 99.97% PC 8 0.003 0.03% 100.00% PC 9 0.000 0.00% 100.00% The factors loading matrix of principal components 1 to 4 is calculated (Table 4) and the importance coefficient of each factor is obtained (Table 5) by multiplying the factors load matrix and the contribution rate of the principal components.
Table 4. Load matrixes of factors.
Factors PC 1 PC 2 PC 3 PC 4 Pop 0.025 −0.223 0.683 0.261 GDP 0.076 0.093 0.088 0.606 PGDP 0.051 0.316 −0.595 0.345 DT 0.104 0.118 0.099 0.606 PT 0.017 0.035 0.030 0.018 AT 0.283 0.394 0.227 −0.242 R 0.365 0.679 0.197 −0.130 H 0.872 −0.453 −0.178 −0.016 Dist 0.075 0.074 0.197 −0.046 Table 5. The importance coefficient of factors
Factors Importance coefficient H 0.397 R 0.374 AT 0.268 DT 0.126 GDP 0.103 Dist 0.085 Pop 0.081 PT 0.023 PGDP 0.022 Thus, according to the PCA result, the determinant of the airline passenger volume includes railway and highway passenger volume as well as total retail sales of social consumer goods of the departure and arrival city.
-
Four factors, including railway passenger volume, highway passenger volume, and the total social consumer goods retail value of departure and arrival cities are considered as independent variables to build the prediction model. To ensure data stability and reduce the impact of absolute error and heteroscedasticity, all data were log-transformed.
To eliminate multicollinearity and improve the accuracy of the model, a variance inflation factor (VIF) analysis was conducted to detect multicollinearity in regression analysis. If the VIF is less than 5, there is no multicollinearity. If the VIF is between 5 and 10, there is a moderate degree of multicollinearity, which is often considered acceptable in practice. However, when the VIF is greater than 10, there is considerable multicollinearity[30,31]. An appropriate method must be adopted to address multicollinearity, as it can distort or reduce the accuracy of predicted values due to highly correlated relationships between variables. As shown in Table 6, the VIF of each variable is less than 10, suggesting that there is no significant multicollinearity or that the collinearity between variables is negligible.
Table 6. Result of multicollinearity test.
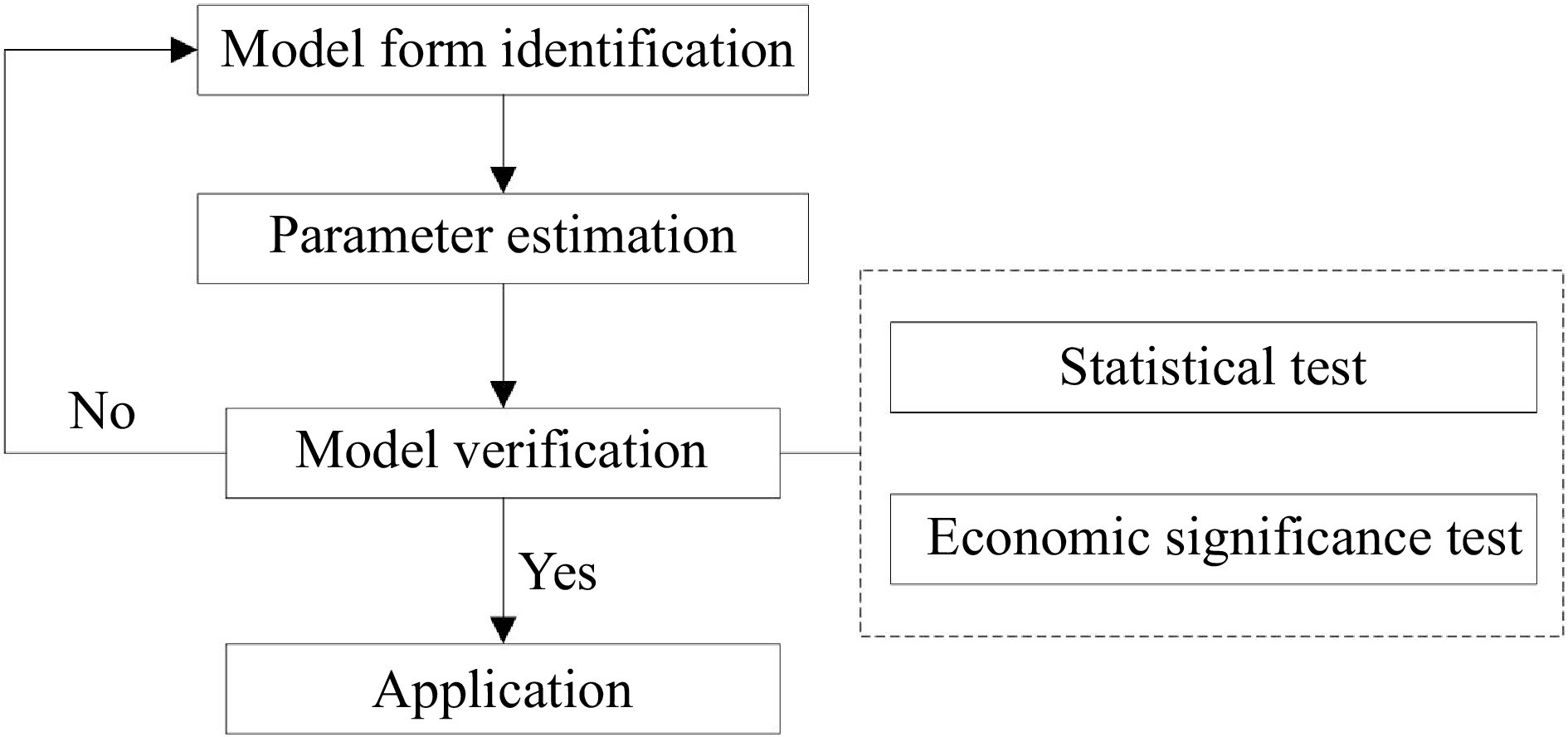
Variables H R AT DT VIF 1.339 5.623 5.391 1.480 Figure 1 shows the construction process, and Eviews is used to develop a prediction model.
Model form identification
-
In general, the panel data model can be divided into three parts.
If a panel data model is defined as Eqn (1), it is a pool model or a multivariate regression model whose regression coefficient and constant remain unchanged for any individual and time point.
$ {\rm{y}}_{\rm{i}\rm{t}}={\alpha }+{\rm{X}}_{\rm{i}\rm{t}}{\beta }+{{\varepsilon }}_{\rm{i}\rm{t}},\;\rm{i}=\rm{1,2},3\dots \rm{N};\;\rm{t}=\rm{1,2},3\dots \rm{N};\;\rm{t}=\rm{1,2},3\dots \rm{T} $ (1) where, α represents the constant; β is the coefficient;
$ {X}_{it} $ $ {\varepsilon }_{it} $ If a panel data model is defined as Eqn (2), it is a fixed effects model whose regression coefficient remains fixed and the constant changes with the individual or time point.
$ {\rm{y}}_{\rm{i}\rm{t}}={{\alpha }}_{0}+{{\alpha }}_{\rm{i}}+{{\gamma }}_{\rm{t}}+{\rm{X}}_{\rm{i}\rm{t}}{\beta }+{{\varepsilon }}_{\rm{i}\rm{t}},\;\rm{i}=\rm{1,2},3\dots \rm{N};\;\rm{t}=\rm{1,2},3\dots \rm{T} $ (2) where, α0 represents the fixed constant; αi and γ refers to the constant changing with an individual and time point. When αi equals 0 but γt does not, it is called a time-fixed effects model; When γt equals 0 but αi does not, it is called an entity fixed effects model; when both αi and γt equal 0, it is a pool model; when neither αi nor γt equals 0, it is an entity and time-fixed effects model.
If a panel data model is defined as Eqn (3), it is a random effects model whose regression coefficient maintains fixed and the constant is a stochastic variable that is not related to time point or individual.
$ {\rm{y}}_{\rm{i}\rm{t}}={{\alpha }}_{{\gamma }}+{\rm{X}}_{\rm{i}\rm{t}}\rm{\beta }+{{\varepsilon }}_{\rm{i}\rm{t}},\;\rm{i}=\rm{1,2},3\dots \rm{N};\;\rm{t}=\rm{1,2},3\dots \rm{T} $ (3) where, αr represents the stochastic variable that is not related to time point or individual.
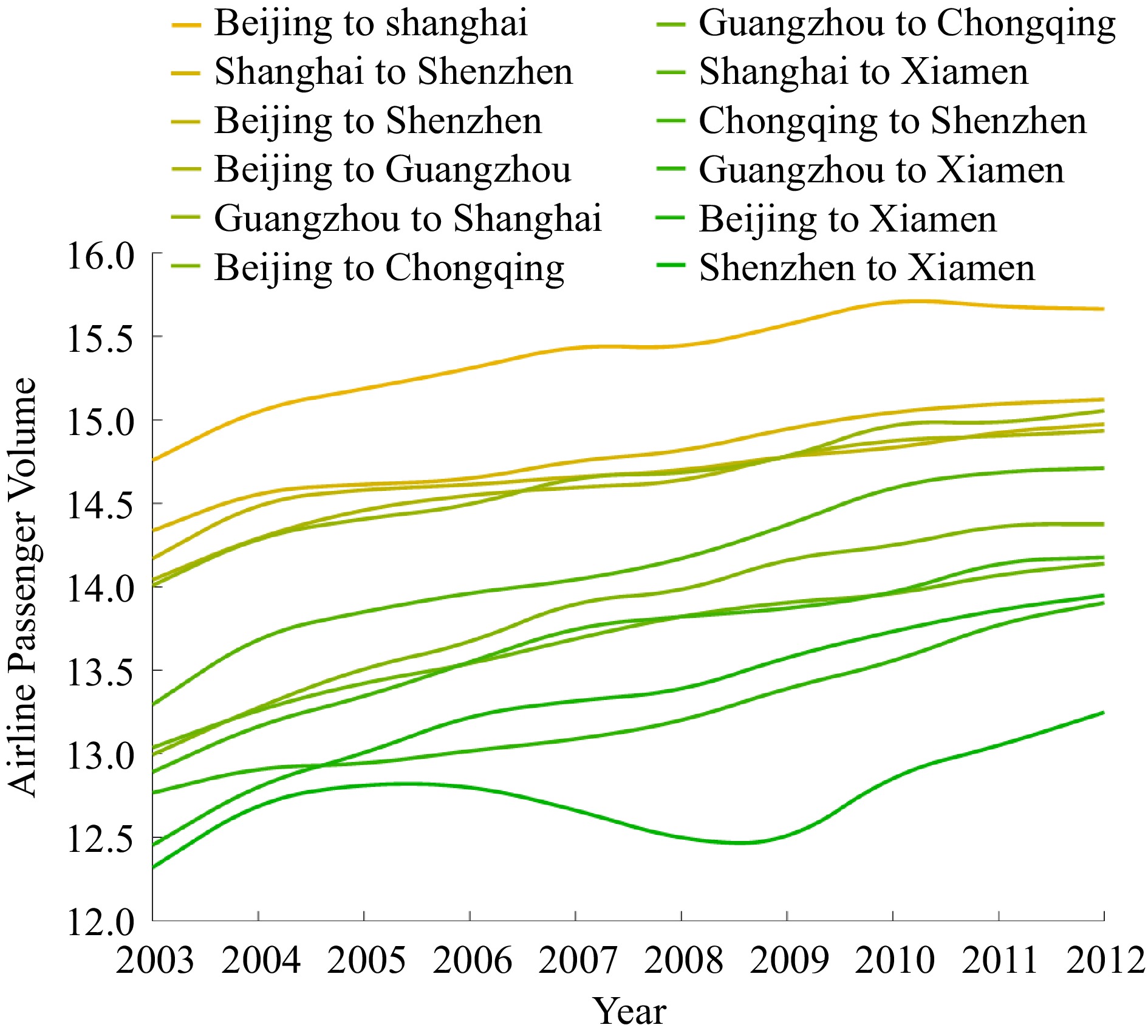
The period of panel data collected from 2003 to 2012 is relatively short, and Fig. 2 illustrates that all airline passenger volumes increased from 2003 to 2012, and each airline had its own relatively stable growth rate. In addition, the intercept of each airline has striking differences, which might be attributed to the different development stages and characteristics of each city. The time-fixed effects model assumes the same coefficient but varying intercepts across time periods, which aligns well with the assumption. Therefore, the time fixed effects model was adopted in this paper.
Parameter estimation and analysis
-
Table 7 presents the results of the panel data model as specified in Eqn (2) and the multivariate regression model as specified in Eqn (1). Figure 3 visualizes the regression results and compares the performance of the panel data model and the multivariate regression model.
Table 7. Estimation results and statistical test results of model
Variables Panel data model
coefficientsMultivariate regression
model coefficientsC 3.256*** (3.274) 6.957*** (14.671) H −0.120*** (−10.981) −0.165*** (−12.109) R −0.081*** (4.010) 0.075 (1.622) AT 0.754*** (17.138) 0.606*** (9.769) DT 1.107*** (8.305) 0.588*** (9.567) R2 0.912 0.881 Adj-R2 0.902 0.877 F−statistic 84.991 212 Prob (F−statistic) 0.000 0.000 MAPE (%) 1.342 1.608 RMSE 0.235 0.288 *, **, and *** indicate that the explanatory variable is significant at the 0.10, 0.05, and 0.01 significance level, respectively. t-statistics are printed in parentheses. 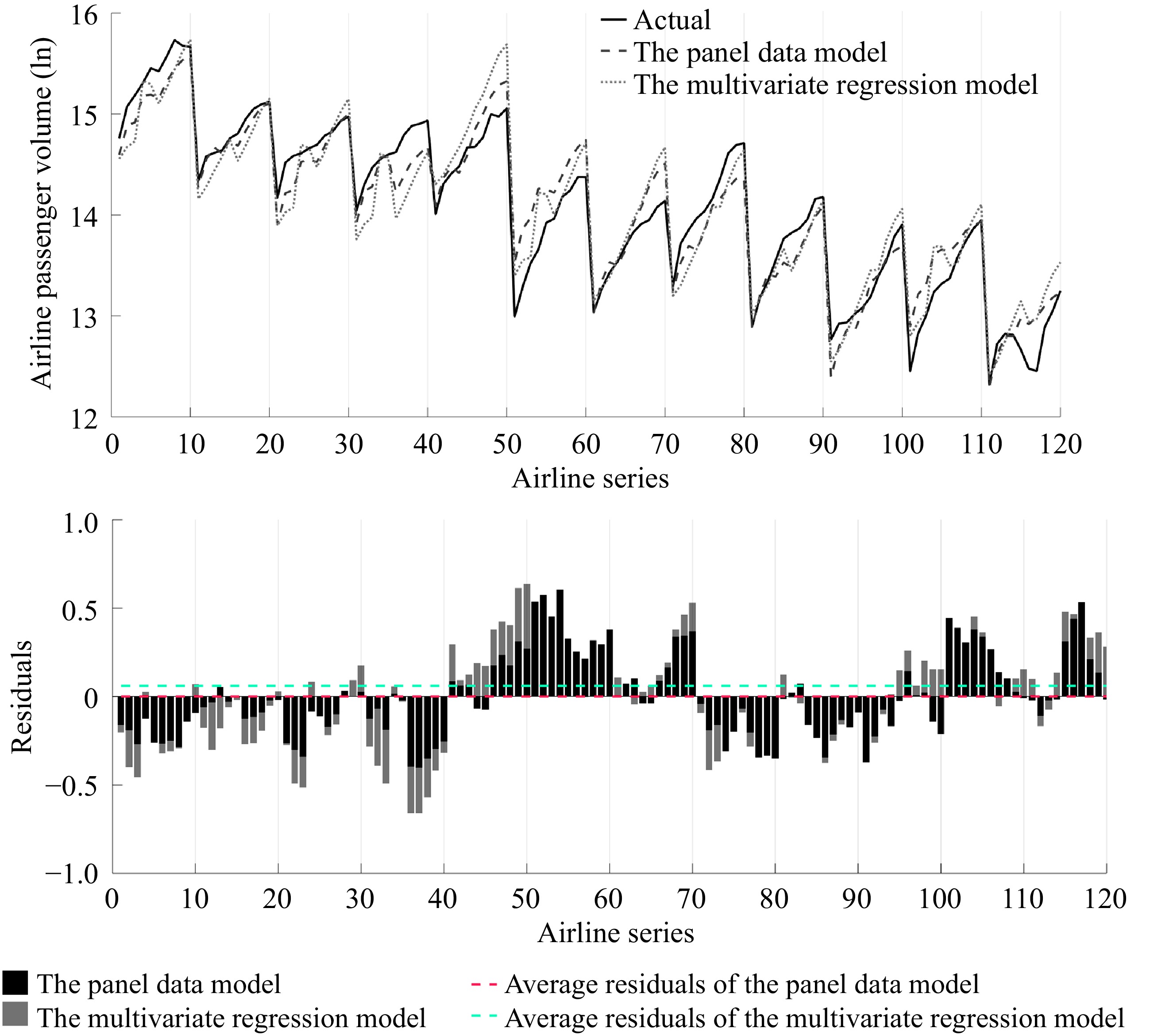
Figure 3.
The panel model and the multivariate regression model for the airline passenger volume projection (2003−2012).
All the coefficients in the panel data model are statistically significant at the 0.01 significance level. The model has a good fit with an adjusted R2 of 0.902, indicating a highly accurate regression with the small values of MAPE and RMSE. However, it is worth noting that the multivariate regression model exhibits a lower adjusted-R2 of 0.877 and higher value of mean absolute percentage error (MAPE) and root mean square error (RMSE) when compared with the panel data model. More remarkable, it contradicts the PCA results that railway passenger volume is statistically insignificant in the model.
The impacts of the total retail sales of social consumer goods of departure and arrival cities appear to be strongly significant in the prediction model. For a departure city, this metric represents the consumption capacity and level of residents, and its growth promotes consumption upgrading. For an arrival city, it reflects the consumption capacity of both residents and tourists. These imply that airline passenger volume increases if the total retail sales of social consumer goods increase. Specifically, a 10% higher total retail sales of social consumer goods in an arrival city corresponds to approximately a 7.5% higher airline passenger volume. Similarly, 10% higher total retail sales of social consumer goods of a departure city lead to an 11.07% increase in airline passenger volume.
Arguably most interesting is the negative and statistically significant effect of highway and railway passenger volume on airline passenger volumes. Highway and railway transportation diverts airline passenger volume and reduces airline passenger volume, which means that if more people travel by railway or highway transportation, then the volume of air travel decreases. A 10% higher highway passenger volume yields a 1.2% lower airline passenger volume, and a 10% higher railway transportation passenger volume yields a 0.8% lower airline passenger volume. One might argue that the degree of influence of railway passenger volume should be higher than highway passenger volume because railway transport is the most common trip model. However, considering the period of data used in this paper, from 2003 to 2012, most residents traveled by highway transport, and in 2012, the passenger volume of highway transportation was approximately 18 times more than railway transportation. The rapid development of railways, especially the construction of high-speed railways, will greatly impact airline passenger volume.
Hence, the prediction model can be written as Eqn (4).
$ {\ln}Vol=-0.12{\ln}H-0.081{\ln}R+0.754{\ln}AT+1.107DT+3.256+{\gamma }_{t}+{\varepsilon }_{it} $ (4) where, γt is a time point disturbance term shown in Table 8.
Table 8. Time point disturbance term.
Time point Disturbance value 2003 −0.092 2004 0.083 2005 0.215 2006 0.330 2007 0.507 2008 0.713 2009 0.826 2010 1.011 2011 1.232 2012 1.354 -
The airline passenger volumes from Chongqing to Shanghai were used to analyze the effectiveness of the panel data model. According to Chongqing and Shanghai Statistical Yearbook data, variable values are presented in Table 9.
Table 9. Variables values of airline from Chongqing to Shanghai.
Year H R AT DT 2003 18.554 15.704 7.785 6.840 2004 18.826 16.073 7.885 6.974 2005 18.772 15.479 8.000 7.113 2006 18.903 15.638 8.124 7.266 2007 19.165 16.158 8.262 7.445 2008 19.523 16.396 8.429 7.672 2009 19.614 16.413 8.559 7.830 2010 19.911 16.602 8.730 8.023 2011 19.975 16.716 8.880 8.238 2012 20.162 16.838 8.967 8.390 Taking each variable data into the panel data model and the multivariate regression model, the predicted value, and the precision are calculated and shown in Table 10. Comparison between the predicted and the actual values shows that the prediction accuracy of the two models from 2003 to 2012 is more than 90%, however, note that only the regression results of the panel model are proven to be statistically significant at the 0.01 significance level, which can provide reliable support for decision-making related to airport operation and management.
Table 10. Comparison of predicted value and actual value.
Year Actual
valuePanel model Multivariate
regression modelPredicted value Precision Predicted value Precision 2003 12.811 13.552 94.21% 13.813 92.17% 2004 13.141 13.848 94.62% 13.935 93.96% 2005 13.47 14.045 95.73% 14.051 95.69% 2006 13.59 13.998 96.99% 14.207 95.46% 2007 13.605 14.141 96.05% 14.391 94.22% 2008 13.698 14.404 94.84% 14.584 93.53% 2009 14.026 14.576 96.08% 14.742 94.89% 2010 14.185 14.735 96.12% 14.925 94.78% 2011 14.281 14.907 95.62% 15.140 93.99% 2012 14.43 14.972 96.25% 15.260 94.25% -
Appropriate forecasting models are of significant value to the aviation sector. They aid airport operators in deciding which routes to adjust and which new routes to introduce. In this study, the determinants of airline passenger volume were identified through PCA, and a prediction model was established accordingly. Three major findings were derived from this analysis.
First, four factors, namely railway and highway passenger volume, as well as the total retail sales of social consumer goods in departure and arrival cities, were proven to be the key determinants of airline passenger volume. The research analyzed nine potential factors of airline passenger volume from geo-economic and service-related perspectives and identified these four key factors using PCA. Second, considering both cross-section characteristics and time trends, an airline passenger volume prediction model was proposed after undergoing statistical and economic significance testing. The panel data model, which exhibited highly accurate regression with low MAPE and RMSE values, outperformed the multivariate regression model. Finally, the model was applied to predict airline passenger volume from Chongqing to Shanghai, and it performed well, achieving an accuracy of over 90%. In practice, these results can be leveraged by airline companies to assist in making adjustments to their flight schedules and highlighting the need for new routes.
-
The authors confirm contribution to the paper as follows: study conception and design: Wang X; analysis and interpretation of results: Wang X, Cai J; draft manscript preparation:Wang X, Cai J, Wang J; data collection: Cai J, Wang J. All authors reviewed the results and approved the final version of the manuscript.
-
The datasets generated during and/or analyzed during the current study are not publicly available, but are available from the corresponding author on reasonable request.
This research was funded by The National Natural Science Fund of China (No. U1564201 and No. U51675235). The authors would like to show great appreciation for the support.
-
The authors declare that they have no conflict of interest.
- Copyright: © 2024 by the author(s). Published by Maximum Academic Press, Fayetteville, GA. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
-
About this article
Cite this article
Wang X, Cai J, Wang J. 2024. A panel data model to predict airline passenger volume. Digital Transportation and Safety 3(2): 46−52 doi: 10.48130/dts-0024-0005
A panel data model to predict airline passenger volume
- Received: 07 April 2024
- Revised: 19 May 2024
- Accepted: 27 May 2024
- Published online: 27 June 2024
Abstract: Airline passenger volume is an important reference for the implementation of aviation capacity and route adjustment plans. This paper explores the determinants of airline passenger volume and proposes a comprehensive panel data model for predicting volume. First, potential factors influencing airline passenger volume are analyzed from Geo-economic and service-related aspects. Second, the principal component analysis (PCA) is applied to identify key factors that impact the airline passenger volume of city pairs. Then the panel data model is estimated using 120 sets of data, which are a collection of observations for multiple subjects at multiple instances. Finally, the airline data from Chongqing to Shanghai, from 2003 to 2012, was used as a test case to verify the validity of the prediction model. Results show that railway and highway transportation assumed a certain proportion of passenger volumes, and total retail sales of consumer goods in the departure and arrival cities are significantly associated with airline passenger volume. According to the validity test results, the prediction accuracies of the model for 10 sets of data are all greater than 90%. The model performs better than a multivariate regression model, thus assisting airport operators decide which routes to adjust and which new routes to introduce.