Bus frequency optimization in a large-scale multi-modal transportation system: integrating 3D-MFD and dynamic traffic assignment

Public transport is a key component of a sustainable transport system. In many cities, public transport is considered as a promising solution to urban traffic congestion. A properly designed public transport system is expected to improve traffic efficiency by minimizing the total delays of citizens. In a multi-modal system, buses can take more passengers, while moving slower than private cars. A high-frequency bus service would decrease the average traffic speed and hence increase traffic delays, while a low-frequency bus service would increase the waiting time of passengers at bus stops. As argued in literature, the waiting time at bus stops is a key element in a passenger's assessment of bus service quality^[1,2]. The bus service quality could affect the demand for each transport mode, e.g., buses and cars. Hence, the bus frequency can be optimized to minimize the total delays of the transport system, including the time spent by both bus passengers and car users. To optimize bus frequency, it is necessary to integrate the congestion dynamics and its impacts on the mode choices in the optimization formulation.

Optimizing bus frequency will help improve the bus service and alleviate traffic congestion, because a good bus service could reduce car demand. However, in most of the literature on bus frequency optimization, the demand is static^[3−6]. The static demand ignores the interactions between buses and cars, and its impacts on travelers' mode choices. The static demand assumption rules out impacts of bus service on the demand elasticity.

The interaction between cars and buses would determine the travel speed and delays of each mode, which will finally shape the demand for each mode. To predict the mode choice, it is necessary to model the multi-modal congestion dynamics. However, the congestion dynamics in bus frequency optimization is frequently modeled by a Bureau of Public Roads (BPR) function. The BPR function is too simple to describe the multi-modal congestion dynamics. Some attempts^[7,8] have considered multi-modal congestion dynamic when optimizing the public transport system. The interaction between cars and buses is described by a 3D-MFD based model. But the demand including a car demand and a public transport passenger demand, is given exogenously. That is, the impacts of traffic congestion and the bus system performance (e.g., the waiting time at bus stops) on travelers' mode choices are ignored. More details about bus frequency optimization approach can be referred to in Ibarra-Rojas et al.^[9].

To the best of the authors' knowledge, a bus frequency optimization model that can describe impacts of bus frequency on traffic network performance - in terms of mode choices and traffic delays - is still missing. In this paper, we aim to fill the gap by providing a bi-level programming model that integrates the multi-modal traffic dynamics and its impacts on mode choices.

A bi-level programming approach is often used to solve the bus frequency optimization problem^[10−13]. The bi-level optimization model consists of an upper and a lower-level model. The upper-level model finds a bus frequency to accomplish an objective which is often referred to as minimizing the total passenger travel time, total passenger waiting time, transfer time, fare function, bus operation cost, or a combination of all of them^[12,14−17]. In this work, the upper-level objective consists of the bus operation cost and the total time spent of all travelers. The lower level includes a dynamic traffic assignment (DTA) and a dynamic network loading (DNL) model^[11,18−21]. The network loading model often gives travel time, based on which the vehicles are distributed over time and routes.

Consider a megacity, which is partitioned into several reservoirs. The reservoir partitioning algorithm can be referred to in Ambühl et al.^[22]. The traffic dynamics in reservoirs is governed by a three-dimensional macroscopic fundamental diagram (3D-MFD). The 3D-MFD relates the accumulation of cars and buses to the mean flow (total production) at a regional level^[23,24]. Previous works^[25−27] use the 3D-MFD to model the multi-modal network traffic dynamics. Some may argue the link-based models, such as the link-transmission model(LTM), are often taken to load a traffic network in literature^[28,29]. In a megacity which has hundreds and thousands of links and nodes, the link-bPlease check Ambuhl et al in the references as Ambuhl has an umlaut in the text but not in the reference listased DNL models might be inappropriate due to its high computational complexity. The macroscopic model can be classified into continuum-space^[30−32] and discrete-space models^[33−36]. In the existing literature, the continuum-space model is mostly studied in a network with only a few destinations. At the same time, in order to solve the continuum model numerically, the mesh size of the numerical grid is small so the computational complexity might be too high^[37,38]. In this paper, we develop a 3D-MFD based model in the discrete-space modeling framework.

When modeling the dynamics, it is necessary to distinguish the bus and the car. First, the bus path is fixed, while the private car users might choose the shortest path. Second, in terms of the free-flow speed, buses are slower than cars. Third, the waiting time at bus stops would determine the mode choice. Hence, in this paper the 3D-MFD based model consists of two models: the accumulation-based model^[34,35,39] and the trip-based model^[40−42]. The accumulation model is used to model the car traffic dynamics, while the trip-based model is to model the bus dynamics. The accumulation of buses determines an MFD which relates the outflow to the accumulation of cars. The bus speed is given as a function of the accumulation of cars and buses.

The bi-level model is solved by a surrogate model-based algorithm, which approximates the complex simulation of the primal problem, to greatly reduce the complexity and improve efficiency^[43,44]. The double projection algorithm is taken to solve the lower-level multi-modal DUE problem^[45]. For each OD pair, the dynamic traffic flow on the network is in DUE state when the travel time experienced by travelers departing at the same time is equal and minimal, and no one can reduce the travel time by choosing an alternative route. All regional paths and the total demand profiles between different OD pairs is given.

The contributions of this research are as follows:

First, we develop a 3D-based modeling framework for the large-scale multi-model traffic dynamics. To distinguish the car and the bus, the accumulation-based model and the trip-based model are used to model the congestion dynamics of cars and buses, respectively. Second, we establish DUE conditions considering the travelers' behaviors, and propose a region-based path choice model based on the 3D-MFD modeling. The time-dependent demand of travelers for the bus line is affected by the mode and path choice. A variational inequality model for multi-mode is present, solved by a double projection algorithm. Third, we propose a bi-level programming model where the upper-level model minimizes a cost function for the road users and the operating company, and the lower-level includes a Mode Choice-dynamic traffic assignment (DTA) model and takes into account the interactions between cars and buses using a 3D-MFD based model. The surrogate model-based algorithm is embedded to solve the bi-level programming problem.

The remainder of this paper is organized as follows: The problem description is given in the next section, which is followed by a section that introduces the 3D-MFD based models to describe the traffic dynamics at the regional level. Then we introduce the bi-level programming model considering the bus frequency and the solution algorithms. The Numerical study section gives numerical examples. Finally, concluding and our future research directions are given in the last section.

Consider a transport network consisting of cars and buses, respectively. The city network is partitioned into $N$ reservoirs. To optimize the bus frequency, we formulate the problem based on Assumptions 1−3.

Assumption 1: Each reservoir is governed by a well-defined 3D-MFD, see Fig. 1. The 3D-MFD describes the production as a function of the car accumulation and the bus accumulation, see Fig. 1b.

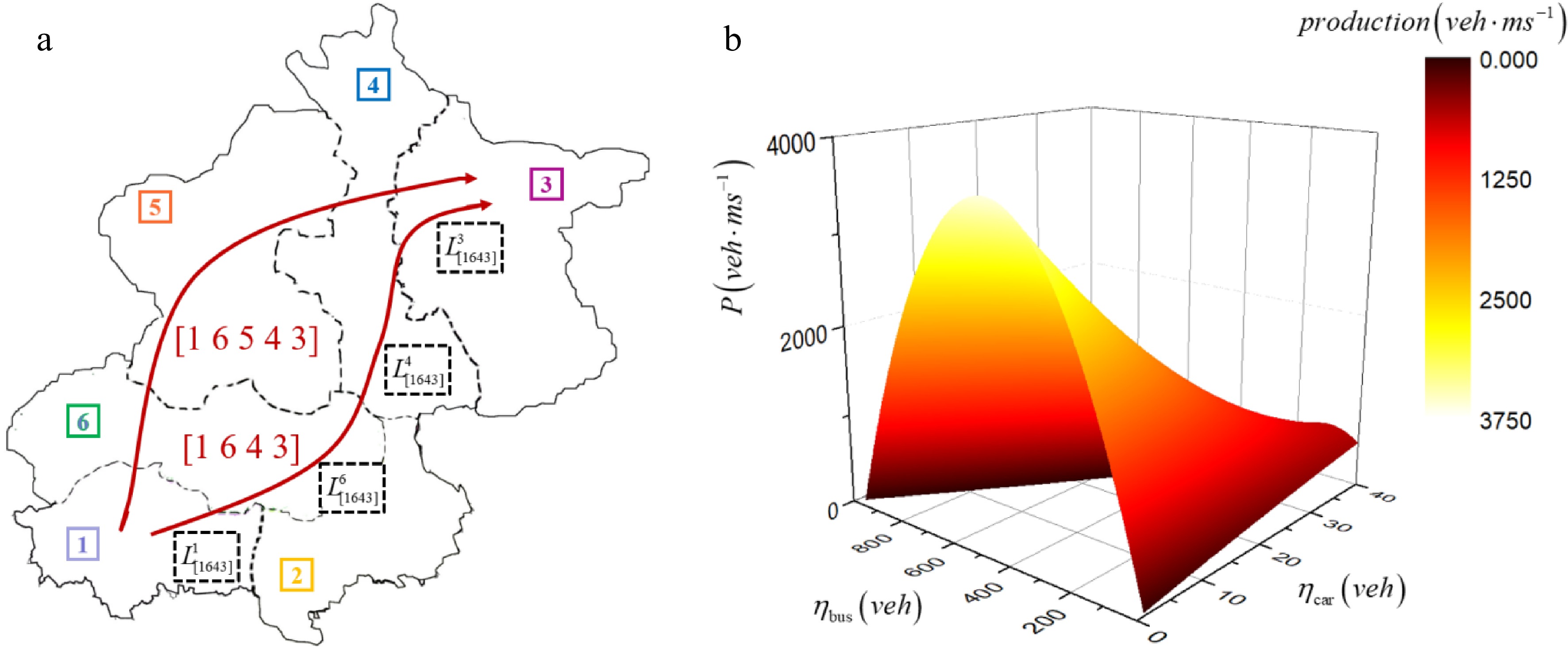
Figure 1. 

A multi-reservoir network. (a) Network partitioning and characteristics. (b) 3D-MFD surface which the formula refers to Paipuri & Leclercq^[27].

Assumption 2: Buses' free flow speed is lower than cars. The bus would travel at free-flow speed if the car speed is not lower than the bus speed. This assumption means the bus and the cars share the urban road space. The 3D-MFD shows the impacts of bus flow on the private cars. The bus speed would not be influenced by cars unless the car speed is lower than the bus free-flow speed.

Assumption 3: Travelers' behaviors follow a DUE rule. This assumption indicates that the travelers make decisions on modal and routing choices based on network performances.

A regional path (macroscopic path) $p$ is defined as a succession of reservoirs from the origin reservoir to the destination reservoir. The path represents the route of cars or the bus line. Fig. 1a shows two regional paths, for illustration, i.e., [1 6 5 4 3] and [1 6 4 3] between the OD pair (1−3). The average trip length in reservoir $r$ along path $p$ is denoted as ${L_{{\text{p,r}}}}$. $R$ is the set of path section along the path $p$, the total trip length along path $p$ is denoted as $ {L_{\text{p}}} = \sum\nolimits_{{\text{r}} \in {\text{R}}} {{L_{{\text{p,r}}}}} $. Vehicles leave the reservoir when they finish their trip distance in that reservoir. For illustration, Fig. 1a displays the ${L_{{\text{p,r}}}}$ in each reservoir which is compose of the path [1 6 4 3], and the total average trip length ${L_{\left[ {1643} \right]}}$ is the sum of $L_{[1643]}^1$, $L_{[1643]}^6$, $L_{[1643]}^4$, and $L_{[1643]}^6$. More details about trip length distribution can refer to Batista et al.^[46]. We discretize the time period $T$ into a set of time intervals $K = \left\{ {k = 1,2, \ldots ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{K} } \right\}$, and let $\delta t$ be the time interval length, such as $ \delta t\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{K} = T $.

In this section, we present a macroscopic methodological framework considering two different travel modes. To simulate the traffic dynamics, the accumulation-based model is used for cars, the trip-based model is used for buses. The accumulation of buses in one reservoir determines the MFD for cars. The bus speed is determined by the accumulation of buses and cars.

For each reservoir, traffic dynamics are described by the evolution of accumulation along different paths for each mode $m \in \left\{ {bus,car} \right\}$ is expressed as:

where $\delta t$ is the time step, $\eta _{{\text{p,r}}}^{\text{m}}\left( t \right)$ denotes the accumulation for each mode $m \in \left\{ {bus,car} \right\}$ traveling on path $p$ in the reservoir $r$ at time $t$. $\Delta \eta _{{\text{p,r}}}^{\text{m}}\left( t \right)$ represents the variety of the accumulation along path $p$ in reservoir $r$ at time $t$. $P_{\text{r}}^{\text{m}}$ is defined as the set of paths passing through the reservoir r by different mode.

Accumulation-based model for cars

The multi-reservoir accumulation-based model is introduced by Mariotte et al.^[35], which is an extension of Yildirimoglu & Geroliminis's work^[34]. For cars, $\Delta \eta _{{\text{p,r}}}^{\text{m}}\left( t \right)$ in Eq. (1) is expressed as:

Where $q_{{\text{p,r,in}}}^{{\text{car}}}(t)$ and $q_{{\text{p,r,out}}}^{{\text{car}}}(t)$ represent the effective inflow and outflow along path p in reservoir r at time t, respectively. Depending on whether the origin or destination is inside the reservoir, the evolution of accumulation of path p in Eq. (1) can be divided into four types:

(i) If r is the origin reservoir but not the destination, we assume the demand generated inside the reservoir without any restrictions. The effective inflow of path $p$ is defined as $q_{{\text{p,r,in}}}^{{\text{car}}}\left( t \right) = \lambda _{\text{p}}^{{\text{w,car}}}\left( t \right){\text{ }}$, $\lambda _{\text{p}}^{{\text{w,car}}}\left( t \right)$ is the path demand for OD pair $w$ by car. Let $q_{{\text{p,r,out}}}^{{\text{car}}}\left( t \right)$ represent the transfer flow from reservoir r to ${p^ + }\left( r \right)$, which is the next reservoir in the reservoir sequence of path p. The effective outflow is calculated as $q_{{\text{p,r,out}}}^{{\text{car}}}\left( t \right) = \eta _{{\text{p,r}}}^{{\text{car}}}\left( t \right)L_{{\text{k,r}}}^{{\text{car}}}/\eta _{{\text{k,r}}}^{{\text{car}}}\left( t \right)L_{{\text{p,r}}}^{{\text{car}}}\min \left( {\mu _{{\text{k,r}}}^{{\text{car}}}\left( t \right),O_{{\text{k,r}}}^{{\text{car}}}\left( t \right)} \right)$ referring to Mariotte et al.^[35] and Mariotte & Leclercq^[42], where $O_{{\text{k,r}}}^{{\text{car}}}\left( t \right)$, $\mu _{{\text{k,r}}}^{{\text{car}}}\left( t \right)$ are the outflow demand (trip completion rate) and the restriction supply for path $k$ in reservoir $r$ of cars respectively. $k$ is the most constrained path: $k = \arg \mathop {\min }\limits_{p \in {P^{\text{r}}}} \mu _{{\text{p,r}}}^{{\text{car}}}\left( t \right){\text{/}}O_{{\text{p,r}}}^{{\text{car}}}\left( t \right)$.

(ii) If r is the destination reservoir but not the origin, the outflow of path $p$ is not limited. Hence, $\mu _{{\text{p,r}}}^{{\text{car}}}\left( t \right) = + \infty $. For effective inflow, $q_{{\text{p,r,in}}}^{{\text{car}}}\left( t \right) = q_{{\text{p,}}{{\text{p}}^{{-}}}\left( {\text{r}} \right){\text{,out}}}^{{\text{car}}}\left( t \right)$, ${p^ - }\left( r \right)$ is the previous reservoir of the reservoir r on path p.

(iii) If r is neither the origin reservoir nor the destination reservoir, the calculation of effective outflow and effective inflow are referred to (i) and (ii) respectively.

(iv) If r is both origin reservoir and destination reservoir, the calculation of effective inflow and effective outflow are referred to (i) and (ii) respectively.

Now we focus on the effective inflow and effective outflow of transfer flow which passes through the boundary entering the reservoir or leaving the reservoir.

As defined by Geroliminis & Daganzo^[47], the trip completion rate is proportional to the total production in each reservoir, defined as $O = P/L$. P is the total production and L is the total network length. The outflow demand is allocated according to the proportion of the accumulation along each path in the reservoir to the total accumulation in the reservoir.

The outflow demand $O_{{\text{p,r}}}^{{\text{car}}}\left( t \right)$ can be derived as:

where $L_{{\text{p,r}}}^{{\text{car}}}$ is the average trip length in reservoir $r$ along path $p$ by car. $\eta _{\text{r}}^{{\text{car}}}\left( t \right)$ and $\eta _{\text{r}}^{{\text{bus}}}\left( t \right)$ are the total accumulation of cars and buses in reservoir r at time t, ${\text{P}}_{\text{r}}^{{\text{crit}}}\left( {\eta _{\text{r}}^{{\text{bus}}}\left( t \right)} \right)$ and $\eta _{\text{r}}^{{\text{crit}}}\left( {\eta _{\text{r}}^{{\text{bus}}}\left( t \right)} \right)$ are the critical accumulation of cars and maximum production which are related to the bus accumulation in the reservoir. That means, bus accumulation over time influence the shape of the MFD profile due to the different bus frequency.

The restriction outflow supply $\mu _{{\text{p,r}}}^{{\text{car}}}\left( t \right)$ corresponds to the inflow supply $I_{{\text{p,}}{{\text{p}}^{{ + }}}\left( {\text{r}} \right)}^{{\text{car}}}\left( t \right)$ of the next reservoir in the path p by car at time t. The existing literature has proposed different entry supply functions with higher critical value than MFD maximum capacity, and compared their performances^[42]. To simplify the process, we use the reservoir entry supply function mentioned in Paipuri & Leclercq^[27]. ${{\text{P}}_{{\text{S,r}}}}$ represents the entry supply production in reservoir $r$.

For transfer flow, the available entry supply production in reservoir $r$ is ${{\text{P}}_{{\text{S,r}}}} - \displaystyle\sum\nolimits_{p \in P_{{\text{int}}}^{\text{r}}} {L_{{\text{p,r}}}^{{\text{car}}}\lambda _{\text{p}}^{{\text{w,car}}}} $, the average trip length for transfer flow is $ \displaystyle\sum\nolimits_{p \in P_{\text{r}}^{{\text{ext}}}} {\eta _{{\text{p,r}}}^{{\text{car}}}\left( t \right)} {\text{/}}\displaystyle\sum\nolimits_{p \in P_r^{ext}} {\eta _{{\text{p,r}}}^{{\text{car}}}\left( t \right)/L_{{\text{p,r}}}^{{\text{car}}}} $ defined by Little's formula^[48]. The reservoir total inflow supply ${I^{\text{r}}}$ is the ratio of the two values.

At the same time, considering the capacity constraints of the reservoir and the nodes at the boundary, we use the sequence of macroscopic nodes corresponding to the reservoir successions of path $p$. The finite number of nodes on the reservoir boundary is denoted as set $N_{\text{r}}^{{\text{bd}}}$, each node is written as $n$. The path through node $n$ to enter the reservoir is recorded as $P_{{\text{r,n}}}^{{\text{car}}}$. A detailed definition of macroscopic nodes has been given in Mariotte et al.^[35]. We use a two-layer merging function also proposed in this paper to calculate restriction inflow supply for transfer flow.

where ${\text{Merge}}\left( \cdot \right)$ function is the inflow merge function mentioned in Leclercq & Becarie^[49]. The available supply or capacity is shared among the paths according to their merge coefficients and ensures the available supply or capacity can be used effectively. Where ${D_{\text{n}}}$ is the capacity of the macroscopic node $n$ on the boundary, which can be expressed as the aggregation of the capacity of all links connected with the node $n$. $\lambda _{{\text{p,r}}}^{{\text{car}}}$ is the inflow demand of path $p$ in reservoir $r$ by car. For transfer flow, the value is equal to outflow demand $O_{{\text{p,}}{{\text{p}}^{{- }}}\left( {\text{r}} \right)}^{{\text{car}}}$ from the previous reservoir. The merge parameter $\alpha _{\text{p}}^{\text{r}}$ is calculated as $\lambda _{\text{p}}^{\text{r}}/\sum\nolimits_{p \in P_{{\text{r,m}}}^{{\text{car}}}} {\lambda _{\text{k}}^{\text{r}}} $. The second-layer merging function is described as follow:

where $P_{{\text{r,bd}}}^{{\text{car}}}$ is the path crossing the boundary into the reservoir $r$ by car. The main difference between the first layer and the second layer merging function is that one considers the capacity constraint of the node on the boundary and the other considers the reservoir supply restriction. $I_{{\text{p,r}}}^{{\text{car}}}\left( t \right)$ is the inflow supply of path p in reservoir r by car at time t.

Then the evolution of car accumulation is calculated by Eq. (1). At the same time, the cumulative count curves of each path in reservoir $r$ can be described by Eq. (7). $U_{{\text{p,in}}}^{{\text{car,o}}}\left( t \right)$ and $V_{{\text{p,out}}}^{{\text{car}}{\text{.d}}}\left( t \right)$ represent the entering cumulative curve and the exiting cumulative curve of path $p$ at time $t$ by car, respectively. ${\tau _{{\text{p,car}}}}\left( t \right)$ represents the experienced travel time when passengers leave at time $t$ and choose path $p$ by car.

The relationship between travel time and cumulative flow is:

If $U_{\rm p,in}^{\rm car,o}\left( t \right)$ and $V_{{\text{p,out}}}^{{\text{car,d}}}\left( t \right)$ are strictly monotone functions with respect to time $t$, the dynamic experience travel time is calculated as:

where ${U_{{\rm{p,in}}}^{{\rm{car,o{\text -}1}}}}\left( \cdot \right)$ is the inverse function of $U_{{\rm{p,in}}}^{{\rm{car,o}}}\left( \cdot \right)$.

Here, the travel time of each path $p$ between OD pairs is the experienced travel time ${\tau _{{\text{p,car}}}}\left( t \right)$ when passengers choose the path.

Trip-based model for buses

All buses are traveling at the same speed $v_{\text{r}}^{{\text{bus}}}\left( {\eta _{\text{r}}^{{\text{car}}}\left( t \right),\eta _{\text{r}}^{{\text{bus}}}\left( t \right)} \right)$ in reservoir $r$ at time $t$. The trip distance of bus on path $p$ in each reservoir $r$ is expressed as:

where $L_{{\text{p,r}}}^{{\text{bus}}}$ is the average trip length in reservoir $r$ along path $p$ by bus. The bus enters the reservoir at time $t - T\left( t \right)$ and leaves at time $t$. The bus speed $v_{\text{r}}^{{\text{bus}}}\left( {\eta _{\text{r}}^{{\text{car}}}\left( t \right),\eta _{\text{r}}^{{\text{bus}}}\left( t \right)} \right)$ at each time $t$ depends on the accumulation of cars and buses in the reservoir by 3D-MFD. We used the functional form $v_{\text{r}}^{{\text{bus}}}$ proposed in Paipuri & Leclercq^[27]:

Constants ${\beta _{{\text{c,b}}}}$ and ${\beta _{{\text{b,b}}}}$ represent the marginal effect of cars and buses on bus mean speed which can be estimated with real data, These parameters can be seen specifically in Loder et al.^[24].

We track the bus trip distance until the total trip length $L_{\text{p}}^{{\text{bus}}} = \displaystyle\sum\limits_{r \in R} {L_{{\text{p,r}}}^{{\text{bus}}}} $ is completed, record the experienced travel time ${\tau _{{\text{p,bus,travel}}}}$. At the same time. The accumulation of cars and buses in each reservoir can be obtained by conservation Eq. (1). For buses, $\Delta \eta _{{\text{p,r}}}^{\text{m}}\left( t \right)$ is expressed as:

Where $\eta _{{\text{p,r,in}}}^{{\text{bus}}}\left( t \right)$ and $\eta _{{\text{p,r,out}}}^{{\text{bus}}}\left( t \right)$ respectively represent the number of buses entering and leaving the reservoir $r$ along path $p$ at time $t$. We also assume the demand generated inside the reservoir without any restrictions and the outflow is not limited in the destination reservoir. For the transfer flow, the number of buses entering reservoir ${p^+}\left( r \right)$ is $\eta _{{\text{p,}}{{\text{p}}^ + }\left( {\text{r}} \right){\text{,in}}}^{{\text{bus}}}\left( t \right) = \eta _{{\text{p,r,in}}}^{{\text{bus}}}\left( {t - T\left( t \right)} \right)$, the number of buses leaving reservoir $r$ is $\eta _{{\text{p,r,out}}}^{{\text{bus}}}\left( t \right) = \eta _{{\text{p,}}{{\text{p}}^ + }\left( {\text{r}} \right){\text{,in}}}^{{\text{bus}}}\left( {t - T\left( t \right)} \right)$. Combined with Eq. (1), we can get the accumulation of cars and buses at any time. According to Eq. (11), we can get the bus mean speed at the next time. The trip-based solver algorithm for buses is described in Algorithm 1.

In this paper, the travel time along path $p$, $p \in P_{{\text{bus}}}^{\text{w}}$ includes the in-vehicle travel time ${\tau _{{\text{p,bus,travel}}}}\left( t \right)$ and the waiting time $\tau _{{\rm{p,bus,\omega ait}}}^{\text{w}}$ of passengers at the bus stop. The waiting time is described below.

First we establish a bi-level optimization framework. The upper-level problem minimizes the total time spent of all road users and bus operation cost. The lower-level problem is a region-based dynamic traffic assignment model.

Bi-level optimization framework

The bus optimization problem in a large-scale transportation network is formulated in a bi-level programming framework. The upper-level determines the optimal frequencies, while the lower level determines traffic behaviour decisions, which is formulated as a multi-modal DUE model with a 3D-MFD based network loading model.

Upper-level problem

We consider the total time spent of all road users and the bus operation cost in the upper-level model. The upper-level model is expressed as follows:

where $Z\left( {\mathbf{F}} \right)$ is the objective function, ${\mathbf{F}}$ denotes the bus frequency vector between all OD pairs ${\mathbf{F}} = \left\{ {{{\mathbf{F}}^{\text{w}}},w \in W} \right\}$. ${T_{{\text{system}}}}$ and ${C_{{\text{operation}}}}$ represent the total time spent of passengers $\left( {{\text{person}} \cdot \min } \right)$ and the operating cost $\left( {\$} \right)$ respectively. $\alpha $ and $1 - \alpha $ represent the weight coefficients of the total time spent and the operation cost, respectively. In order to unify the units, we define a time value coefficient $\beta $ (e.g., $\beta = 1.0{\$} /{\text{person}} \cdot \min $). The detailed explanations are as follows:

(1) Total time spent of passengers ${T_{{\text{system}}}}$

The total time spent is the product of the passenger flow and the corresponding path travel time of all paths. It is used to evaluate the bus frequency improvement on the network performance.

The passenger flow $f_{\text{p}}^{\text{w}}\left( {{\mathbf{F}},t} \right)$ and the travel time $\tau _{\text{p}}^{\text{w}}\left( {f_{\text{p}}^{\text{w}}\left( {{\mathbf{F}},t} \right),t} \right)$ refer to the above sections.

(2) Operating cost of buses ${C_{{\text{operation}}}}$

Energy consumption, vehicle depreciation, personnel wages and so on should be considered in the operation cost. This paper assumes that the average single trip operation cost $G_{\text{p}}^{\text{w}}$ in different periods is known. Therefore, the formula of the operating cost of all buses is constructed:

where $N_{\text{p}}^{\text{w}}$ is the total number of buses on path $p$, $p \in P_{{\text{bus}}}^{\text{w}}$.

(3) Constraint condition

Due to the limited number of buses by bus operations, the constraint condition is Eq. (15), and the operating cost cannot exceed the budget $B$. There are many bus lines in the actual bus transport network, so the combination of bus line frequency is huge. Therefore, we give a discrete selection of bus frequency $\left\{ {{\text{F}}_{\text{p}}^{\text{1}},{\text{F}}_{\text{p}}^{\text{2}}, \ldots ,{\text{F}}_{\text{p}}^{\text{n}}} \right\}$ to improve the search efficiency of the algorithm. ${\text{f}}_{\text{p}}^{\text{w}}$ is the frequency of the bus line $p \in P_{{\text{bus}}}^{\text{w}}$, ${\text{F}}_{\text{p}}^{\text{w}} \in {F_{\text{p}}},{F_{\text{p}}} = \left\{ {{\text{F}}_{\text{p}}^{\text{1}},{\text{F}}_{\text{p}}^{\text{2}}, \ldots ,{\text{F}}_{\text{p}}^{\text{n}}} \right\}$ is the alternative frequency set.

Lower-level problem

In this paper, the bus lines and car routes are considered as paths. Travelers choose ones' travel mode and path following the DUE rule. The travel time of bus passengers include in-vehicle time and the waiting time at bus stops. In this model, the OD demand is time-dependent. Considering the time discretization, the DUE condition of the whole network is established as follows:

where $ \mu _{\text{m}}^{\text{w}}\left( k \right) $ is the minimum travel time of travel mode $ m \in \left\{ {bus,car} \right\} $ between OD pair $w$ during the time interval $k$, $ f_{{\text{p,m}}}^{\text{w}}\left( k \right) $ is the flow of path $ p $ in mode $ m $ between OD pair $w$ during the time interval $k$, $ m $ represents bus or car. The total passenger flow between OD pair $w$ is $ {\lambda ^{\text{w}}}\left( k \right) = \displaystyle\sum\limits_{m \in \left\{ {bus,car} \right\}} {\displaystyle\sum\limits_{p \in P_{\text{m}}^{\text{w}}} {f_{{\text{p,m}}}^{\text{w}}\left( k \right)} } $. The sum of any path flow between OD pair $w$ should be equal to demand ${\lambda ^{\text{w}}}\left( k \right)$, and limit all path flows to be nonnegative. $\tau _{{\text{p,m}}}^{\text{w}}\left( k \right)$ and $f_{{\text{p,m}}}^{\text{w}}\left( k \right)$ indicate that travel time and path flow are determined by the bus frequency.

The DUE condition can be formulated as a variational inequality model. The variables are the path flows, which can be described as Eq. (17). Let ${\mathbf{f}}$ be the vector of all path flows.

Among which $\Omega = \left\{ {{\mathbf{f}} \geqslant 0\left| {\displaystyle\sum\nolimits_{p \in {P_{\text{w}}}} {f_{\text{p}}^{\text{w}}\left( k \right) = {\lambda ^{\text{w}}}\left( k \right)} ,{\text{ }}\forall w \in W, \; k \in K} \right.} \right\}$ is a set of feasible dynamic path flows. The travel time $\tau _{\text{p}}^{\text{w}}$ is divided into the travel time $\tau _{{\text{p,car}}}^{\text{w}}$ and the travel time $\tau _{{\text{p,bus}}}^{\text{w}}$ between OD pair $w$ considering different mode. The travel time of the passengers who choose the path $p$ by car is the experienced travel time $\tau _{{\text{p,car}}}^{\text{w}}$. For those who take buses, the travel time consists of the in-vehicle travel time and the waiting time before boarding. The mathematical expression is as follows:

where $\tau _{{\text{p,bus,travel}}}^{\text{w}}\left( {{\mathbf{F}},k} \right)$ is the in-vehicle travel time of bus which chooses $p \in P_{{\text{bus}}}^{\text{w}}$ when bus frequency ${\mathbf{F}}$ is determined. $\tau _{{\rm{p,bus,\omega ait}}}^{\text{w}}\left( {{\mathbf{F}},k} \right)$ is the average waiting time (min) of passengers who choose the path by bus. Bus frequency directly influences the waiting time of passengers. The waiting time of passengers on each path $p$ is expressed as follows:

where ${\tau _{\text{p}}}\left( a \right)$ is the waiting time of the $a{\text{ th}}$ bus passenger on path $p \in P_{{\text{bus}}}^{\text{w}}$. We can also consider the fuel cost of cars and the ticket price of buses as the basis of mode and routing choice by assuming the passenger cost per unit time.

In this section, we use a double projection algorithm approach to solve the lower-level problem which is formulated as a variational inequality. The surrogate model algorithm is designed to solve the proposed bus frequency optimization problem.

Double projection algorithm used to solve the VI model

The double projection algorithm is used to solve the dynamic traffic assignment problem in our proposed model, see Algorithm 2. The double projection algorithm is a modified method to solve large-scale VI problems. This method avoids the drawback of slow convergence due to consistently small iteration step size. The reinitialization of the step size ${\rho ^{\text{γ }}}$ is described in Algorithm 2. The applicability to solve large-scale equilibrium problems has been demonstrated. $\text{pro}{\text{j}}_{\Omega}$ (·) is an Euclidean projection map onto $\Omega $. ${{\mathbf{f}}^{\text{γ }}}(k)$ and ${\mathbf{\tau }}({{\mathbf{f}}^{\text{γ }}}(k))$ represent the path flow vector and the travel time vector at iteration $\gamma $ during the time interval $k$, respectively.

To evaluate the accuracy of solutions in each iteration in the double projection algorithm, a gap function is required, see Eq. (23).

Where $ {u^{\text{w}}}(k) $ is the minimum travel time between OD pair $w$ during time interval $k$ . Convergence is declared if $ G({\mathbf{f}}) \leqslant \varepsilon $, where $\varepsilon $ is a given convergence threshold value. More details of the double projection algorithm can be found in Panicucci et al.^[45].

Surrogate model-based algorithm use to solve the bi-level programming problem

Consider M bus lines in the network and N alternative bus frequencies. We can generate ${N^{\text{M}}}$ candidate plans for all bus lines. Enumerating all candidate plans to find the optimal solution is unfeasible due to the high computational complexity. The traditional heuristic algorithms for solving the bi-level model is not applicable for the large-scale network optimization problem in this paper. A surrogate-based optimization algorithm is used to solve the bi-level programming model, in which the radial basis function (RBF) is updated to approximate the total time spent of all road users in Eq. (17).

The solution of bus optimization problem is expressed as vector ${\mathbf{y}}$. The objective function value ${\mathbf{Z}}$ can be calculated using Eq. (14). We use a predictive value scoring criterion and a distance scoring criterion based on RBF to predict the best candidate point. The weight coefficient of the distance scores is defined as $w_n^s$. The algorithm ends when the maximum number of iteration ${\gamma _{\max }}$ is reached. Otherwise, we update the RBF in next iteration. The detailed procedure of the surrogate-based optimization algorithm is shown in Algorithm 3. More details of surrogate model-based algorithm can refer to Liu & Wang^[50] and Regis^[51].

In this section, we conduct numerical case studies to test the performance of the proposed large-scale bus frequency optimization framework. The studied network and simulation scenarios are described in the Network structure section. The simulation results are given in the Results section. We firstly display the convergence of double projection algorithm, the result of dynamic traffic assignment, and the network traffic dynamics. Then we display the convergence process of surrogate model-based algorithm. Furthermore, we compare the optimal results in four scenarios and show the effect of our proposed model considering 3D-MFD and dynamic user equilibrium. All experiments are run on a computer with an Intel(R) Core (TM) i7 3.60 GHz and 16.0 GB RAM.

Network structure

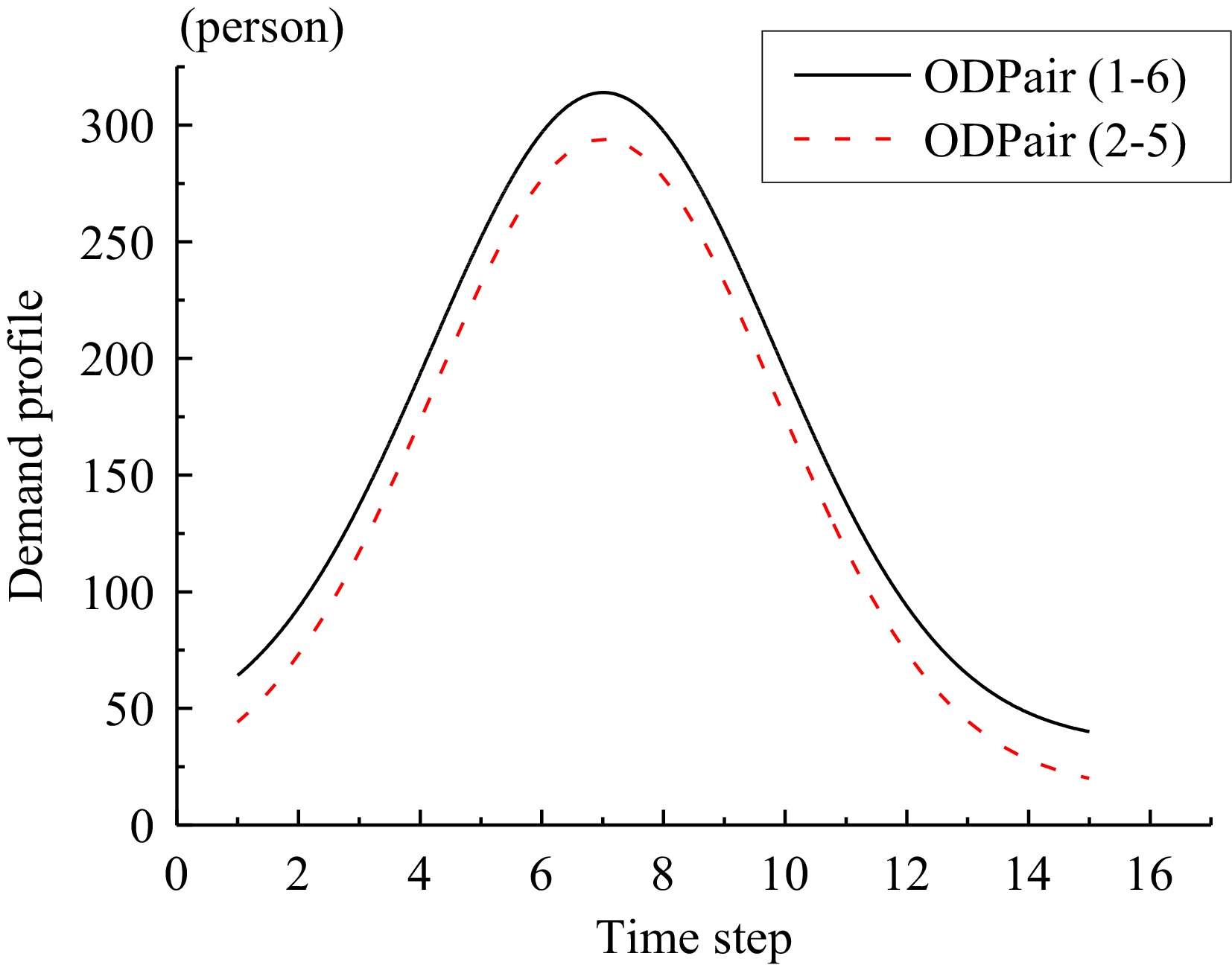
The case study network consists of six reservoirs, including two regional OD pairs (1-6, 2-5) and eight paths (four car routes and four bus lines), as shown in Fig. 2. Each reservoir has a well-defined 3D-MFD. The 3D-MFD used in this paper as shown in Fig. 1b. The macroscopic paths sequence are as follows: four car routes $\left[ {{R_1}{\text{ }}{R_2}{\text{ }}{R_3}{\text{ }}{R_6}} \right]$, $\left[ {{R_1}{\text{ }}{R_4}{\text{ }}{R_5}{\text{ }}{R_6}} \right]$, $\left[ {{R_2}{\text{ }}{R_5}} \right]$, $\left[ {{R_2}{\text{ }}{R_3}{\text{ }}{R_6}{\text{ }}{R_5}} \right]$ and four bus lines $\left[ {{R_1}{\text{ }}{R_2}{\text{ }}{R_3}{\text{ }}{R_6}} \right]$, $\left[ {{R_1}{\text{ }}{R_4}{\text{ }}{R_5}{\text{ }}{R_6}} \right]$, $\left[ {{R_2}{\text{ }}{R_1}{\text{ }}{R_4}{\text{ }}{R_5}} \right]$, $\left[ {{R_2}{\text{ }}{R_3}{\text{ }}{R_6}{\text{ }}{R_5}} \right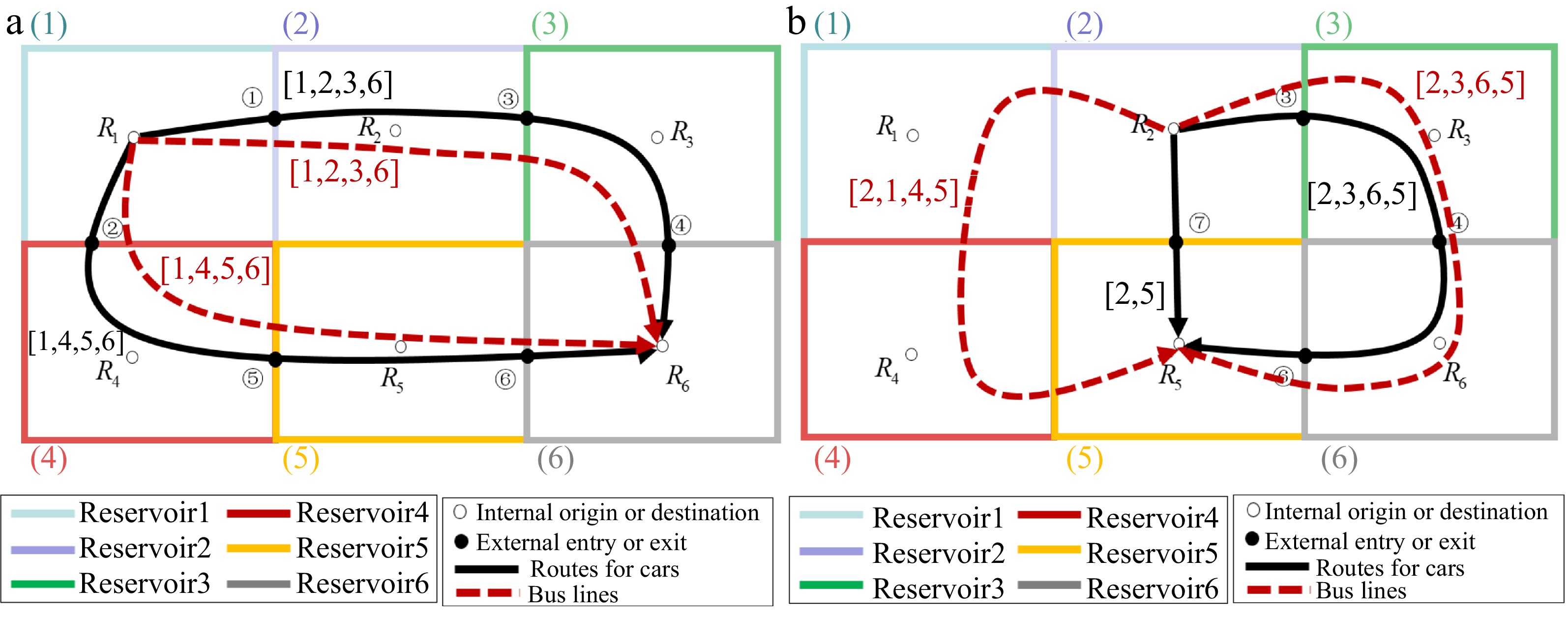]$, corresponding to route 1, 2, 3, 4 and line 1, 2, 3, 4 in the table respectively. The red dotted lines represent the bus lines, and the black solid lines represent the car routes. The study period T = 300 min, time step is $\delta t$ = 60 s. The demand profile is presented in Fig. 3. Assuming that the average passenger of the car is 1.5 persons/veh, and that of the bus is 20 persons/veh.

Figure 2. 

Reservoir system configuration. (a) The regional OD pair (1−6). (b) The regional OD pair (2−5).

Figure 3. 

OD demand profile.

The trip lengths in each reservoir by different paths are referred to in Mariotte & Leclercq^[42]. For the method of estimating the trip length, we refer to Batista et al.^[46] and Mariotte et al.^[35]. The reservoir characteristics $L_{\text{p}}^{\text{m}}$ are presented in Table 1.

In the numerical study, the trip operation cost $G_{\text{p}}^{\text{w}} = 300{\$} /{\rm {veh}}$ for each bus line $p$, bus budget $B = 100000{\$} $, time value coefficient $\beta = 1.0{\$} /{\text{veh}} \cdot \min $. Parameters of surrogate model: disturbance probability ${p_{{\text{slct}}}} = 0.8$, the weight coefficient $w_{\text{n}}^{\text{S}} = 0.6$, the iteration number ${\gamma _{\max }} = 100$.

In particular, we analyze the simulation results when $\alpha = 0.5$. In order to obtain the optimal solution of the model, the optimization model is solved 20 times repeatedly, and the plan with the minimum objective value is selected as the result.

We compare the optimal solution and results in four scenarios:

Scenario 1: Considering 2D-MFD based model and non-equilibrium condition.

Scenario 2: Considering 2D-MFD based model and equilibrium condition.

Scenario 3: Considering 3D-MFD based model and non-equilibrium condition.

Scenario 4: Considering 3D-MFD based model and equilibrium condition.

We optimize the 2D-MFD for each reservoir based on the results obtained by fitting (parabolic fitting) which match the production-MFD well^[35]. The data points are based on the relationship between the production and the accumulation of vehicles in each reservoir obtained by 3D-MFD simulation. The correlation coefficient is expressed as ${R^2}$. When using different 2D-MFD, we also use Algorithm 1 for buses, and the bus speed is still related to the accumulation of cars and buses in the reservoir.

Results

Properties of our proposed model

Convergence process of double projection algorithm

The convergence process of the double projection algorithm to solve the DTA problem is shown in Fig. 4. A stationary Gap value has been reached in 400 iterations.

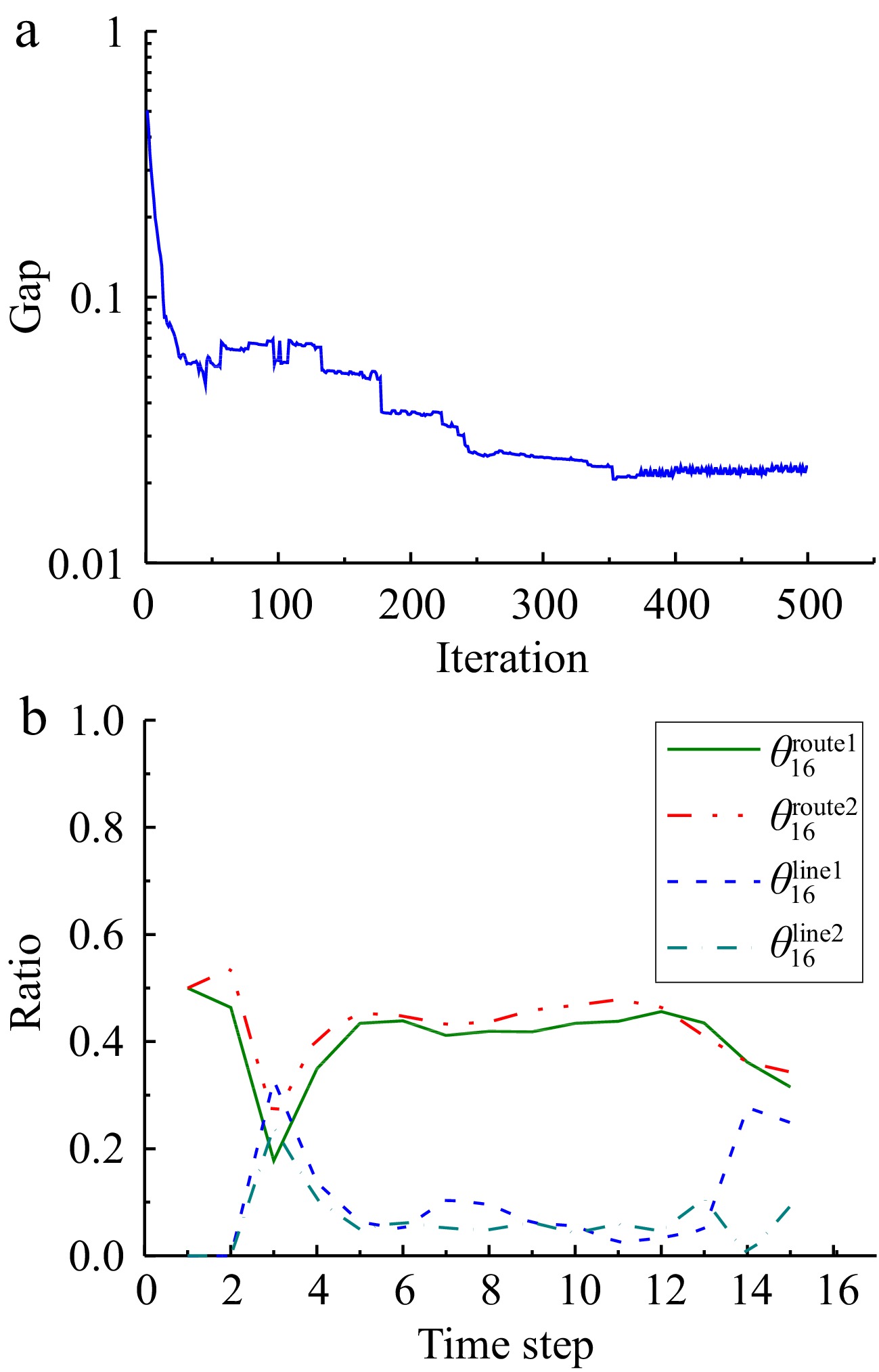
Figure 4. 

Results using double projection algorithm. (a) Convergence of double projection algorithm. (b) Route choice parameters for an OD pair.

Using the double projection algorithm, the mode and route choices of all users at each time can be obtained in Fig. 4b, the proportion of demand between origin 1 and destination 6 that chooses different routes are given. The proportion of demand between OD that choose the route $p$, denoted as $\theta _{{\text{od}}}^{\text{p}}$. For example, the proportion of the demand that chooses the particular regional path 1 and proportion choosing bus line 1 is denoted as $\theta _{{\text{16}}}^{{\text{route1}}}$ and $\theta _{{\text{16}}}^{{\text{line1}}}$, respectively.

Traffic dynamics

Figure 5a shows the evolution of accumulation in Reservoir 1 resulting from the traffic assignment and the 3D-MFD based model with the optimal bus frequency. In order to observe the traffic flow evolution in more detail, we select the first 50 min to observe the changes of the accumulation and outflow of cars in Reservoir 1. When $t = 7$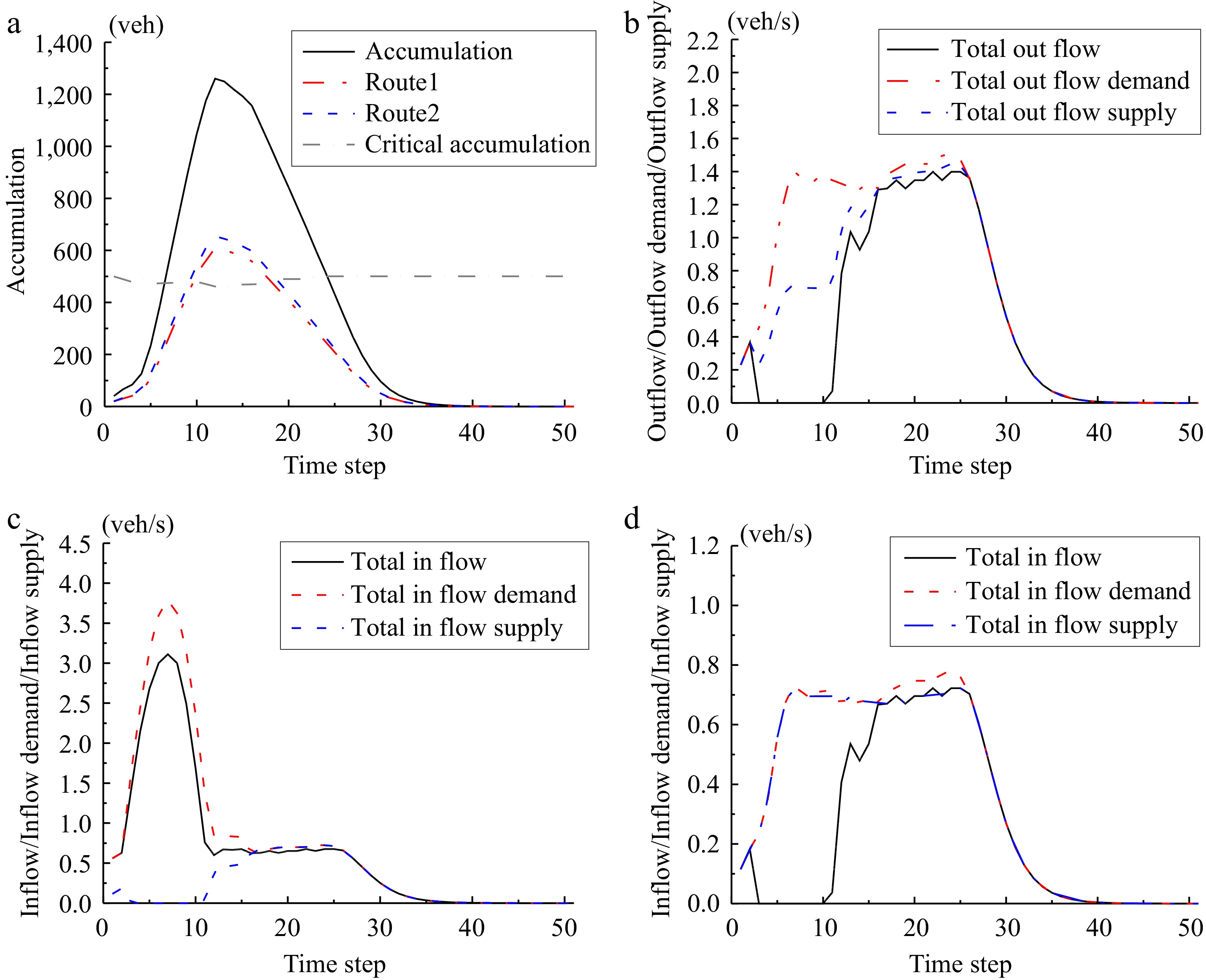, the accumulation of cars in the reservoir exceeds the critical value, and the outflow demand of the reservoir has been rising. It can be seen from Fig. 5b that the outflow of the reservoir is inconsistent with the principle that is the minimum between its outflow demand and an exogenous restriction. This is the result of the interaction between different paths. Figure 5b shows that when calculating the effective outflow, the interaction relationship between different paths in the same reservoir should be analyzed and compared.

Figure 5. 

Traffic dynamics. (a) Evolution of car accumulation in Reservoir 1. (b) Evolution of outflow in Reservoir 1. (c) Evolution of inflow in Reservoir 2. (d) Evolution of inflow in Reservoir 4.

Figure 5c & d display the inflow evolution in Reservoir 2 and Reservoir 4. The black, red and blue curves correspond to the effective inflow, inflow demand and inflow supply respectively. Note that we do not take into account the queue at the reservoir entrance. Because of the generation of travel demand in Reservoir 2 without any constraints, in Fig. 5c we can observe that there is an inflow greater than inflow supply. Since only transfer flow exists in Reservoir 4, inflow will not be greater than that of inflow supply. When the congestion disappears, its inflow supply will gradually increase, which will give more space for cars to enter this reservoir.

Based on the 3D-MFD, the bus speed in different reservoirs can be obtained under the condition that the accumulation of cars and buses are known. We can observe the bus speed evolution in Fig. 6a.

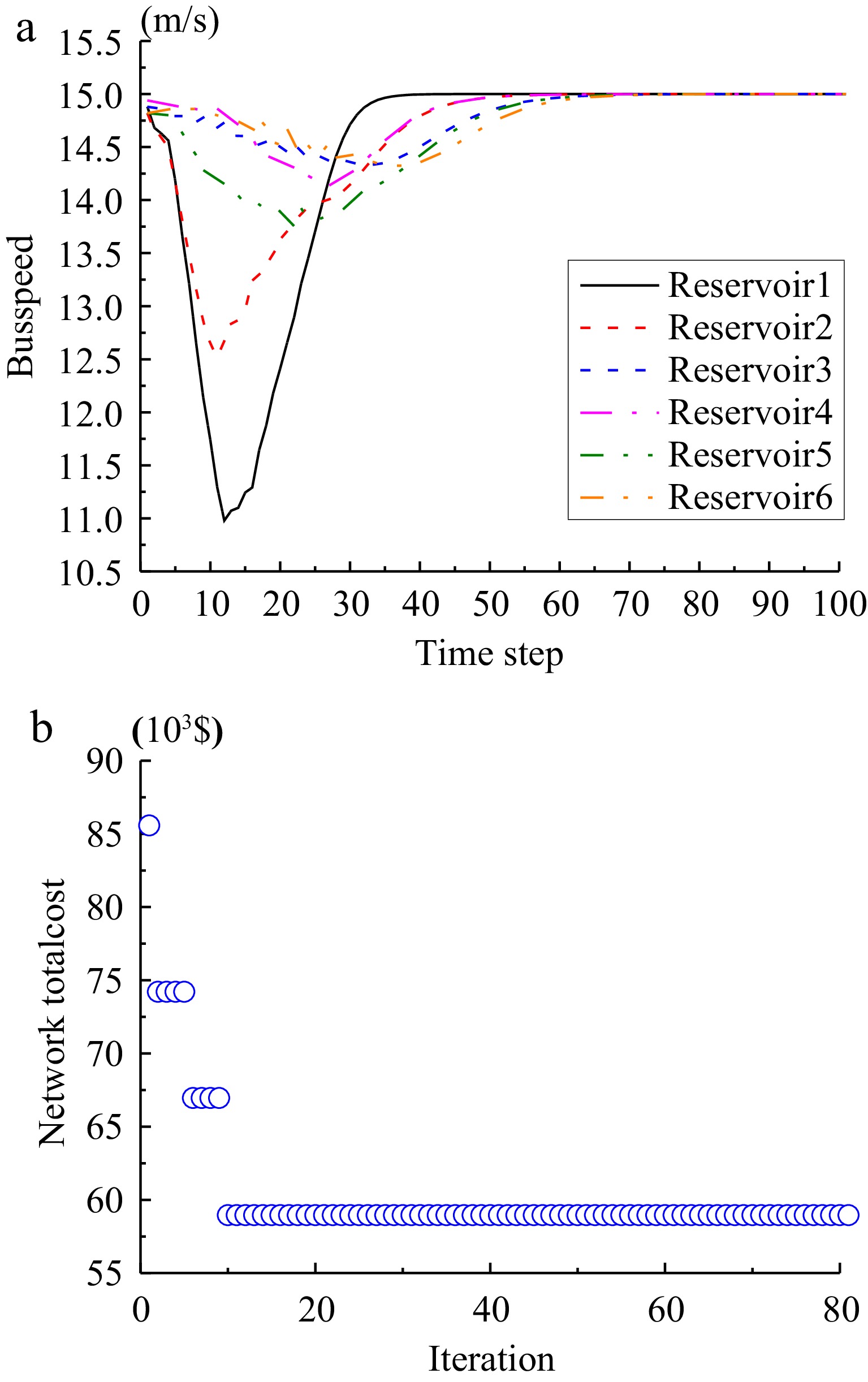
Figure 6. 

Results on the (a) bus speed evolution and (b) convergence of the surrogate model based algorithm.

We display the dynamic path and mode choices of passengers, and the traffic flow evolution model of multi-reservoir can reproduce the traffic dynamics. It can be seen from Yildirimoglu & Geroliminis^[34] that the evolution of congestion predicted by the MFD-based model is consistent with the micro-simulation results, Therefore, the model can predict the effect of route guidance strategy and congestion propagation in a large urban network.

Bus frequency optimization results

Convergence process of surrogate model-based algorithm

We use the surrogate model-based algorithm to solve the bi-level model, the algorithm can reach convergence when iterating to the 10^th generation (see Fig. 6b).

Effect of considering 3D-MFD and dynamic user equilibrium

We compared different simulation results using 2D-MFD and 3D-MFD (Scenario 2 and Scenario 4). The total time spent of passenger and operating cost using 2D-MFD and 3D-MFD respectively are shown in Table 2.

As shown in Table 2, without considering the complex interactions between buses and cars, the optimal frequency of buses is $ \left\{\text{4}\text{.0}，\text{0}\text{.2}，\text{2}\text{.0}，\text{1}\text{.0}\right\}\mathrm{min} $, and the optimized objective value is ${\$} $68755.96. It can be seen that although the total time spent is reduced slightly, the increase of frequency of buses leads to the decrease of waiting time of passengers choosing bus lines, but at the same time, the operating cost of buses will increase significantly, on the whole, the value of the optimized objective value increases greatly.

Then we analyze the results of equilibrium and non-equilibrium conditions using 3D-MFD based model (Scenario 3 and Scenario 4). That is to say, the path demand is known, and the influence of bus frequency optimization on travelers' path choices is not considered. We assume a simple case, that is, all the demands are distributed on each path. First, we analyze the difference optimal solution and objective value between the equilibrium type and non-equilibrium type of assignment models. The simulation results are shown in Table 3. The impact of bus frequency optimization on dynamic traffic assignment will be discussed later. Assuming that the optimal frequency is $ \left\{\text{3}\text{.0},\;\text{4}\text{.0},\;\text{4}\text{.0},\;\text{3}\text{.0}\right\}\mathrm{min} $, the optimal value under the equilibrium condition is ${\$} $58,894.38, and the optimal value under the non-equilibrium condition is ${\$} $106,334.73, which is quite different from the result under the equilibrium state.

Under non-equilibrium conditions, the total travel time of the whole network system is obviously larger than the total time spent with scenario 2.

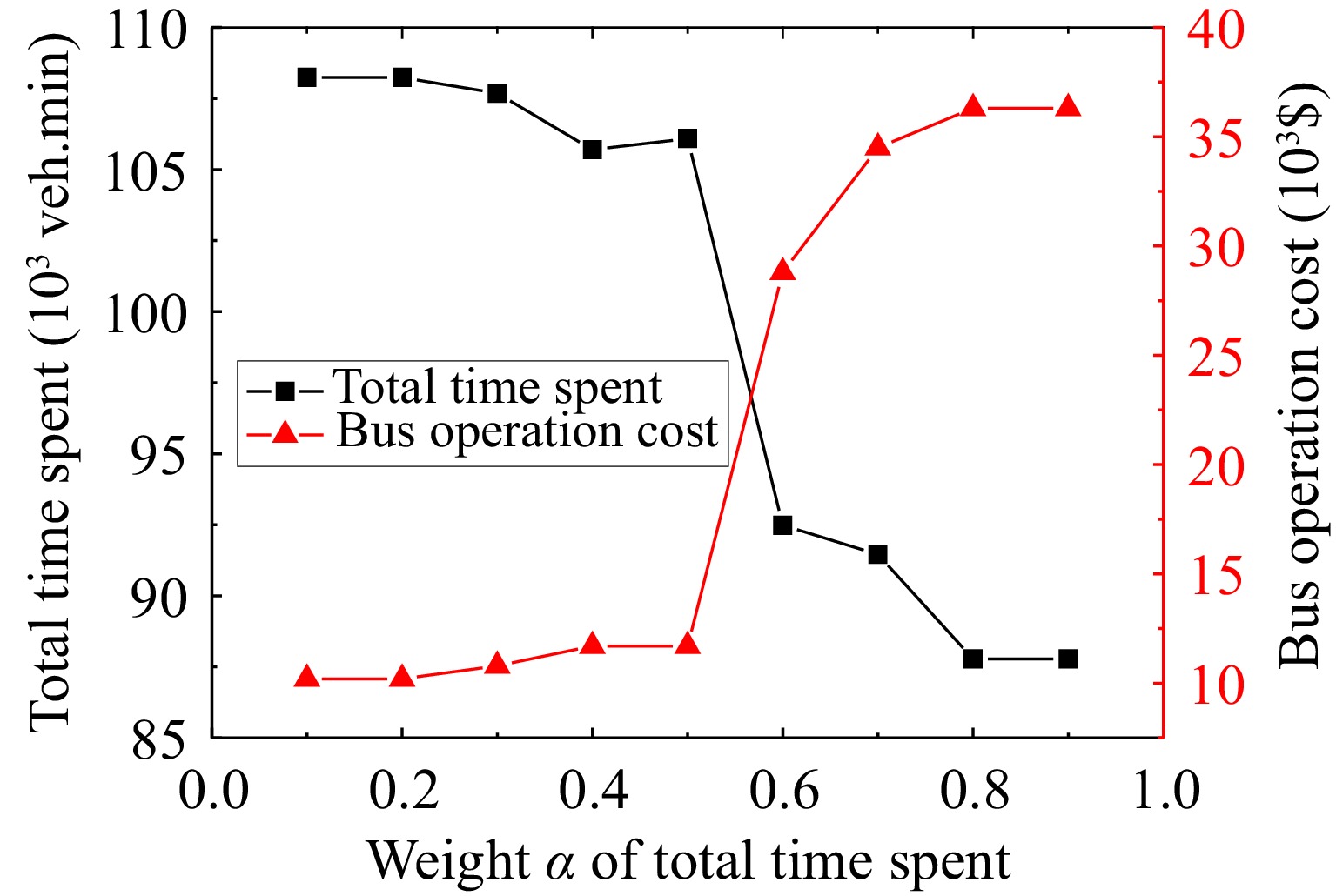
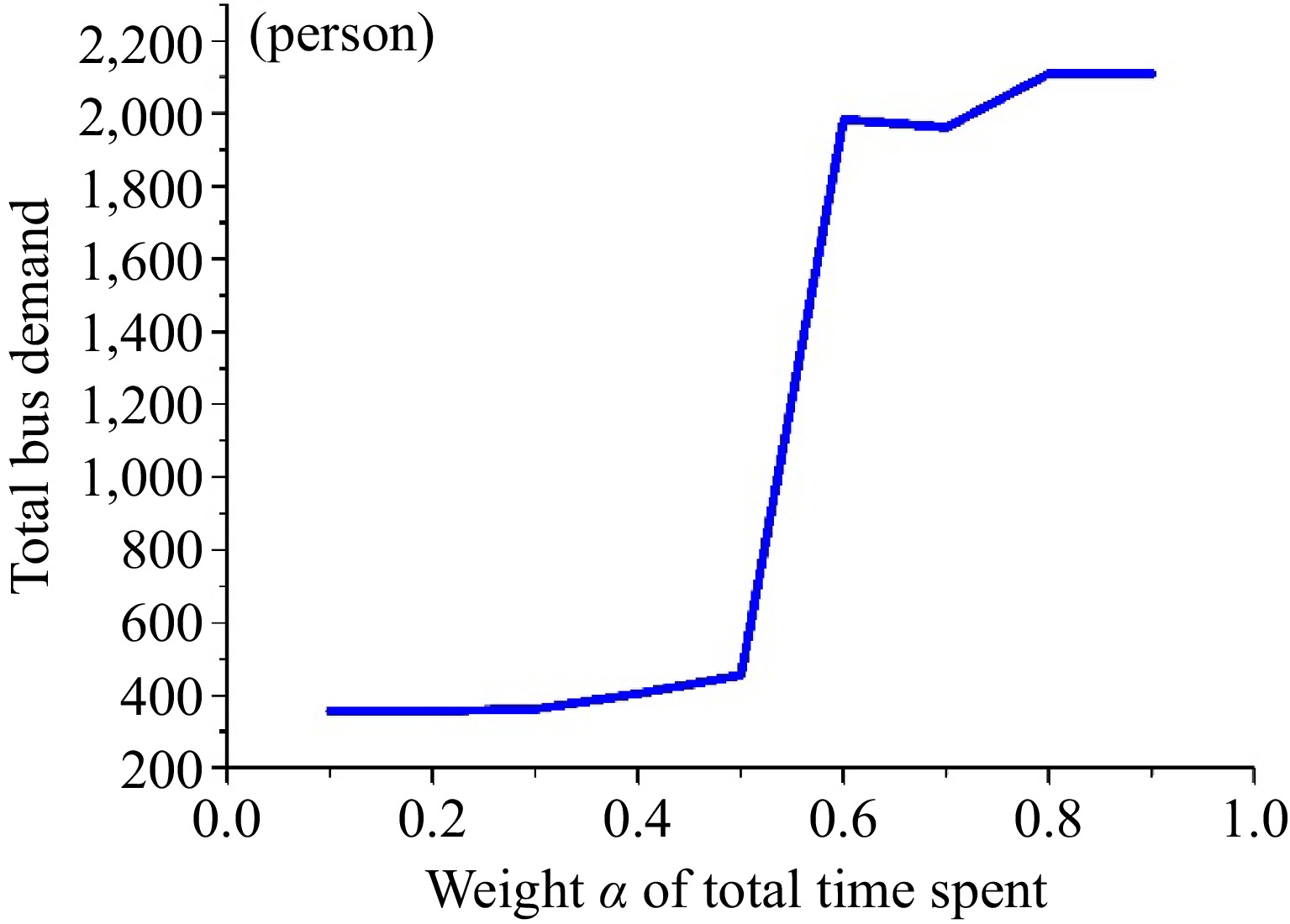
We also analyze the impact of varying the weight of total time spent on the studied system. In Fig. 7, we demonstrate how the weight of total time spent affects the delays and bus operation cost. As the weight (α) increases, , the total time spent decreases while the bus operation cost increases. Figure 8 depicts that the number of people opting for bus transportation increases as the weight (α) of total time spent increases. This suggests that we can encourage a shift towards bus travel by increasing the weight (α).

Figure 7. 

Changes in the total time spent and bus operation cost for different weight values (α).

Figure 8. 

The influence of the total time spent on the demand for bus travel.

Furthermore, we summarize the results of the optimal solution in 4 scenarios: 2D-MFD and 3D-MFD based models are considered under equilibrium and non-equilibrium conditions respectively. We denote ${Z_{\text{i}}}$ as the error in the optimal objective value in scenario $i$ compared to scenario 4. That is, $\Delta {Z_{\text{i}}} = \left[ {{Z_{\text{i}}} - {Z_{\text{4}}}} \right]/{Z_{\text{4}}}$. The results of this comparison are shown in Table 4.

In this paper, the dynamic traffic assignment model based on the 3D-MFD framework is used in the bi-level programming model to find the optimal bus frequency, that is, the bus departure interval is longer than other scenarios, seeing in Table 4, which will increase the waiting time of bus passengers, but in general, the upper level cost is smaller. The proposed bus frequency model integrating 3D-MFD and dynamic traffic assignment can achieve the best optimization results. The results reveal the value of the proposed model. And this new understanding of urban traffic network capacity is very important for formulating new strategies to improve traffic. In the future, we can integrate real-time traffic information or change the bus frequency to significantly improve the network performance.

We propose a bus frequency optimization framework, which considers impacts of traffic dynamics and travel mode choices. We formulate the bus frequency optimization problem as a bi-level programming problem. The upper-level problem minimizes the total time spent of passengers and bus operation cost. To achieve this, we incorporate a region-based dynamic traffic assignment model and a 3D-MFD based dynamics network loading model as the lower-level problem. Travelers determine their mode choices based on travel time, which is calculated using the network loading model. For bus travelers, the travel time comprises the time spent on roads and waiting at bus stops.

In the 3D-MFD based model, we utilize an accumulation-based model to represent car traffic dynamics, while a trip-based model is used for bus dynamics. The accumulation of buses determines an MFD, which relates the average car speed (and the outflow) to the accumulation of cars. The bus speed is dependent on the accumulation of both buses and cars. Whenever a trip distance is completed within a reservoir, the bus exits that reservoir.

To optimize computation time, we employ a double projection algorithm for solving the lower-level multi-modal DUE problem. Additionally, we have developed a surrogate model-based algorithm to solve the proposed bi-level programming problem.

By incorporating these techniques, our framework offers a novel approach to bus frequency optimization that considers traffic dynamics and travel mode choices. Numerical results display the convergence result of two algorithms and the evolution of speed and accumulation in the reservoirs. We also study the bus frequency setting problem in case of multi-modal traffic networks and analyze the influence of the optimal frequency when the weight of passenger total time spent and that of bus operator's cost are changed. Then, we analyze the different optimization results between the 2D-MFD and 3D-MFD based models and equilibrium type and non-equilibrium type of assignment models. Finally, we compare the results of the optimal solution in four scenarios: 2D-MFD and 3D-MFD based model are considered under equilibrium and non-equilibrium conditions respectively. The results reveal the value of considering multimodal interactions and dynamic user equilibrium. This optimization framework ensures that determined bus frequency actually leads to efficient bus service in the transit network.

Promoting modal shift towards public transport, particularly buses, while minimizing the total delays of all travelers, remains a significant research question in practical implementation. To encourage modal shift towards public transport, we propose a bus frequency optimization framework that focuses on improving bus operations. Our model incorporates Dynamic Traffic Assignment (DTA) to analyze modal choices, enabling us to assess the impact of bus operations on the demand distribution between buses and cars. A model without DTA would underestimate the impacts of bus operation on the modal shift and its impacts on the road traffic system.

The proposed framework can be extended to a transportation system with a subway. The extension with a subway is in a straightforward way because it only affects the mode choices. To handle the large-scale problem, this work treats the studied city as a multi-reservoir system. To implement this aggregation approach in real life, we still need to address many other research questions, which would be the future research direction. We propose three research directions: (i) In each reservoir, several bus stops are aggregated as one virtual bus stop. An optimization approach to aggregate these bus stops is required. (ii) We assume the regional average trip length for cars is constant. But regional trip lengths vary over time^[34]. We will further study the impact of heterogeneity of trip length on optimal bus frequency. (iii) The calibration and verification of the model and the algorithms would also need more effort.

The authors confirm contribution to the paper as follows: study conception and design: Long J; analysis and interpretation of results: Cui D, Long J, and Yuan K; draft manuscript preparation: Yuan K, Cui D, and Long J. All authors reviewed the results and approved the final version of the manuscript.

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.