-
The level of development in a country is very much reflected by the quality and extent of its transportation systems[1]. In addition, the condition of roads within a country holds significant importance for its overall development. It serves as a significant indicator of the country's economic level and has been recognized by the World Bank as a criterion for assessing ratings[2]. Considered as a lifeline for a nation, considerable portions of the annual national budget are allocated towards the development and maintenance of road networks[3]. Pavements, as integral components of road networks, require continuous conservation. Over time, the condition of pavements undergoes changes as a result of various factors, including structural strength, traffic loading characteristics, environmental conditions, and maintenance efforts. There are gradual accumulations of damage over the years which are referred to as deterioration ultimately leading to the pavement reaching its serviceability limit. At this stage, the visible signs of internal damage such as cracking, rutting, and potholes, also known as distress, are the indicators of the pavement condition[4]. Research has shown that deteriorating pavement conditions significantly contribute to increased travel time and decreased road safety, leading to a higher number of accidents[5].
The Pavement Management System (PMS) is a valuable planning tool that aids in making decisions regarding the effective and economical maintenance of the road network. Its primary objective is to ensure the comfort and safety of road users while optimizing the allocation of resources in a timely manner[6,7]. By comprehending the process of pavement deterioration, it is possible to predict the necessary resources and operations for mitigating pavement deterioration. The allocation of adequate funding for pavement maintenance poses an ongoing challenge for decision-makers[8]. There is always an ideal time for maintenance and rehabilitation operations. Deterioration rate and maintenance costs will decrease if timely operations are carried out. Pavement performance prediction models are the best tools for the ideal time determination[9].
AASHTO, 2011 categorized pavement maintenance into: (i) reactive and (ii) proactive[10]. Reactive maintenance means conducting activities in response to a system failure[11]. Proactive maintenance is a strategic approach implemented to prevent or delay the occurrence of failures[12]. There are two proactive maintenance approaches: preventive and predictive. Preventive techniques involve scheduled activities aimed at extending the lifespan of an infrastructure. On the other hand, predictive methods rely on inspection analysis to anticipate system failures and schedule necessary maintenance actions accordingly. This type of maintenance aims to prevent those failures from occurring[13]. In recent years, predictive approaches have emerged as highly significant among maintenance strategies. This is primarily attributed to their potential in improving various aspects of maintenance objectives. These approaches help reduce costs over the lifespan of highways, enhance highway performance, enable optimal long-term planning, and incorporate risk management[10,14].
The traditional reactive approach involves replacing roads only after significant structural damage has already occurred. This reactive approach often leads to more extensive and costly rehabilitation measures, posing potential safety hazards for road users before any interventions are made[6,15,16]. The proactive approach prioritizes preservation by implementing minor and less invasive repairs on roads before significant structural degradation takes place. The objective is to minimize the necessity for extensive road reconstruction. In comparison to a reactive approach, a proactive strategy results in long-term cost savings, reduced traffic congestion, and prevents a significant decline in safety conditions[6,17]. The data collection and analysis phases play a critical role in implementing a proactive approach and are fundamental to the success of a Pavement Management System (PMS) implementation[18,19]. Early-stage pavement maintenance has been proven to result in significant cost savings by preventing further deterioration of the pavement. To ensure efficient decision-making by engineering pavement managers, funding is allocated in a manner that prioritizes efficiency and economic viability. An essential component of a robust pavement management system is the collection of extensive road condition data over time. This data is utilized in the development of pavement deterioration models, enabling accurate predictions. Continuous monitoring of pavement degradation forms the foundation of a pavement management system, facilitating the determination of asset degradation rates at both individual and network levels. Additionally, it assists in evaluating the remaining lifespan of the pavement and facilitates the scheduling of future maintenance activities[20,21].
This study reviewed predictive techniques from existing literature to improve the effectiveness and efficiency of maintenance planning. The limitations of these models and their potential impact on accuracy and applicability were also explored. Moreover, an investigation was conducted into the various factors that influence the accuracy of predictive analytics.
-
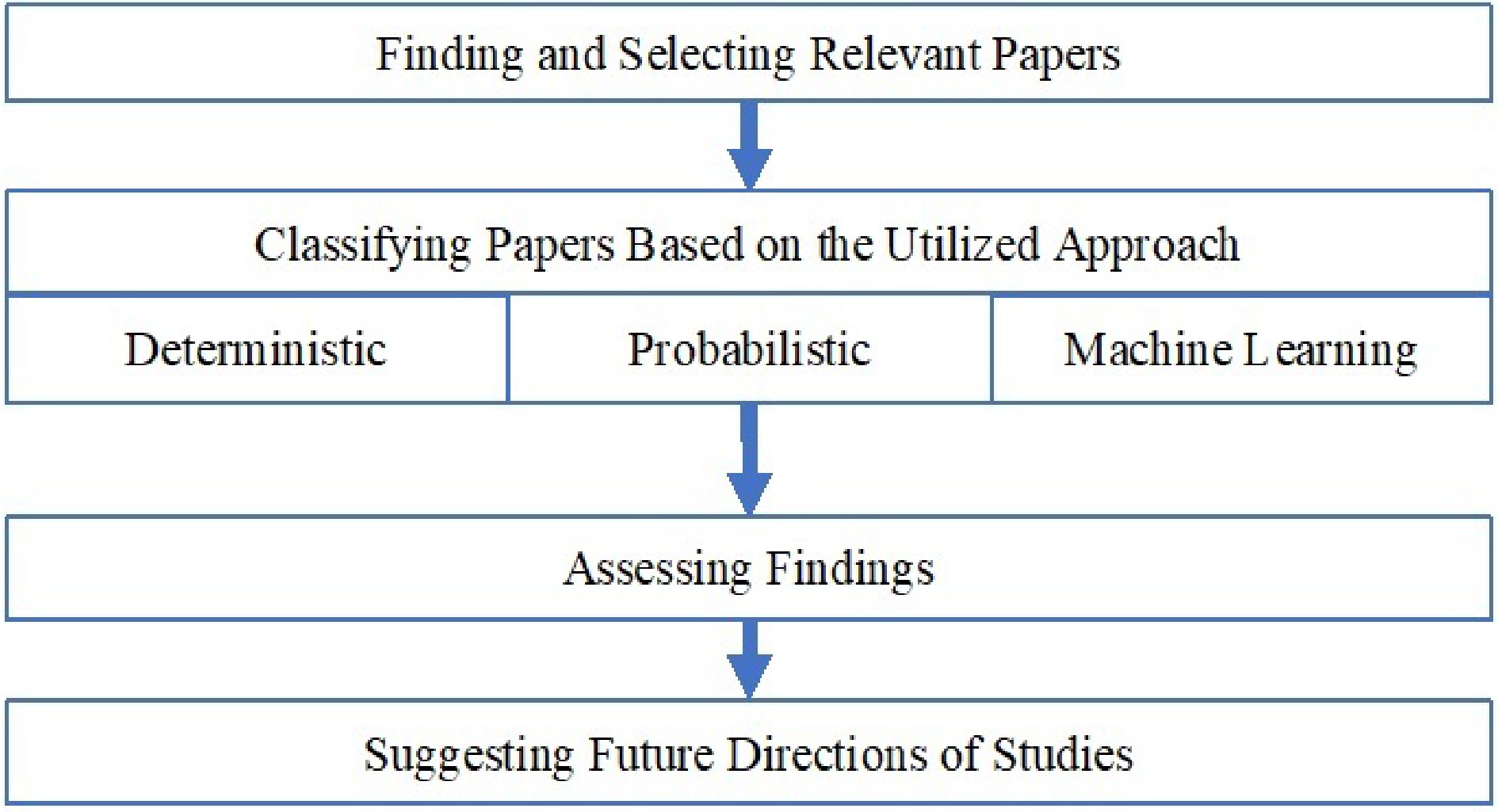
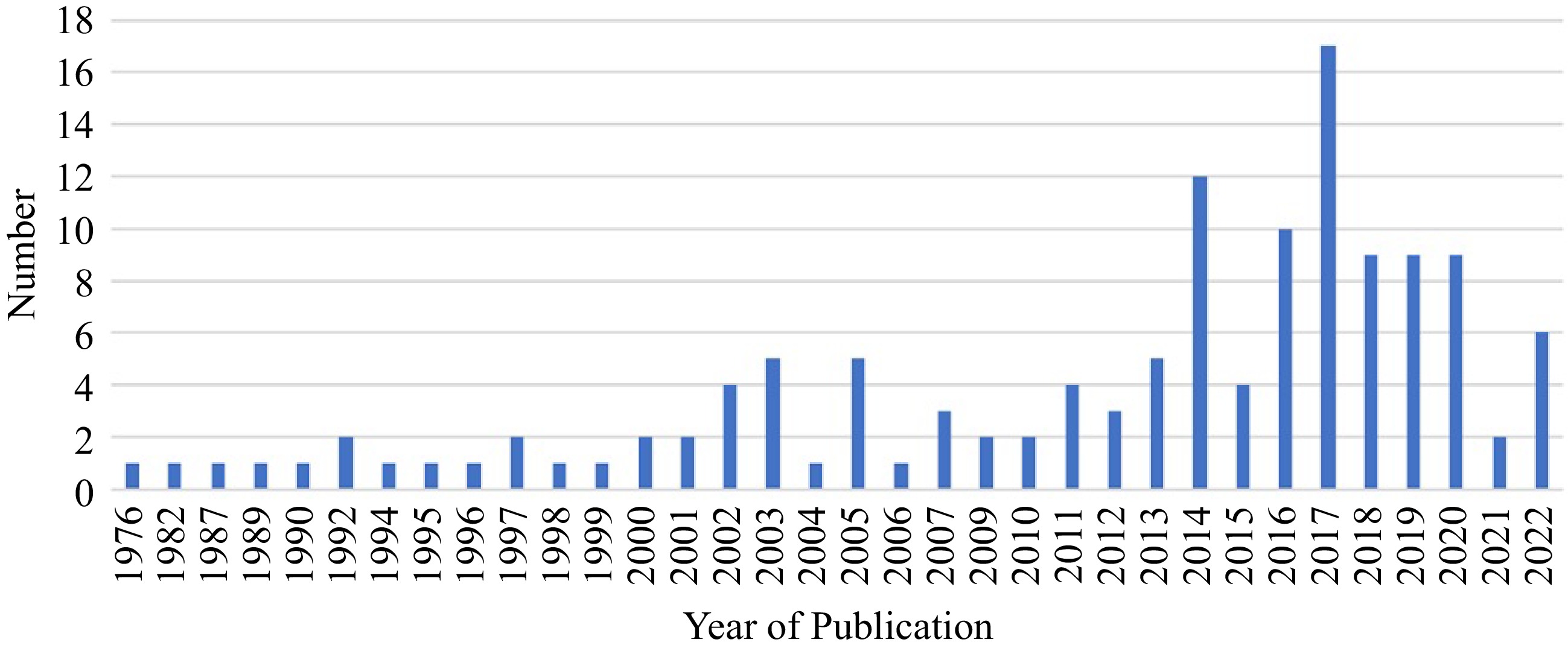
The methodology for the review consisted of several steps, including the selection of relevant papers, categorization of the utilized prediction methods, and evaluation of their limitations and drawbacks. The papers were further analysed based on the algorithms employed to develop prediction models, which were classified into three sub-categories: deterministic, probabilistic, and machine learning. The framework of the methodology is illustrated in Fig. 1. The primary focus was on reviewing papers published within the last 20 years. In this work, a majority of the significant studies that have applied predictive analytics have been covered. Figure 2 provides a visual representation of the total number of papers investigated per year of publication.
-
Deterioration models are utilized to forecast the future condition, performance, or level of service of an asset item. Deterministic models are represented by mathematical functions, whereas probabilistic models employ probability distributions to predict a range of potential conditions or the likelihood of a specific condition occurring in the future[22−24]. Figure 3 illustrates the classification of reviewed prediction models.
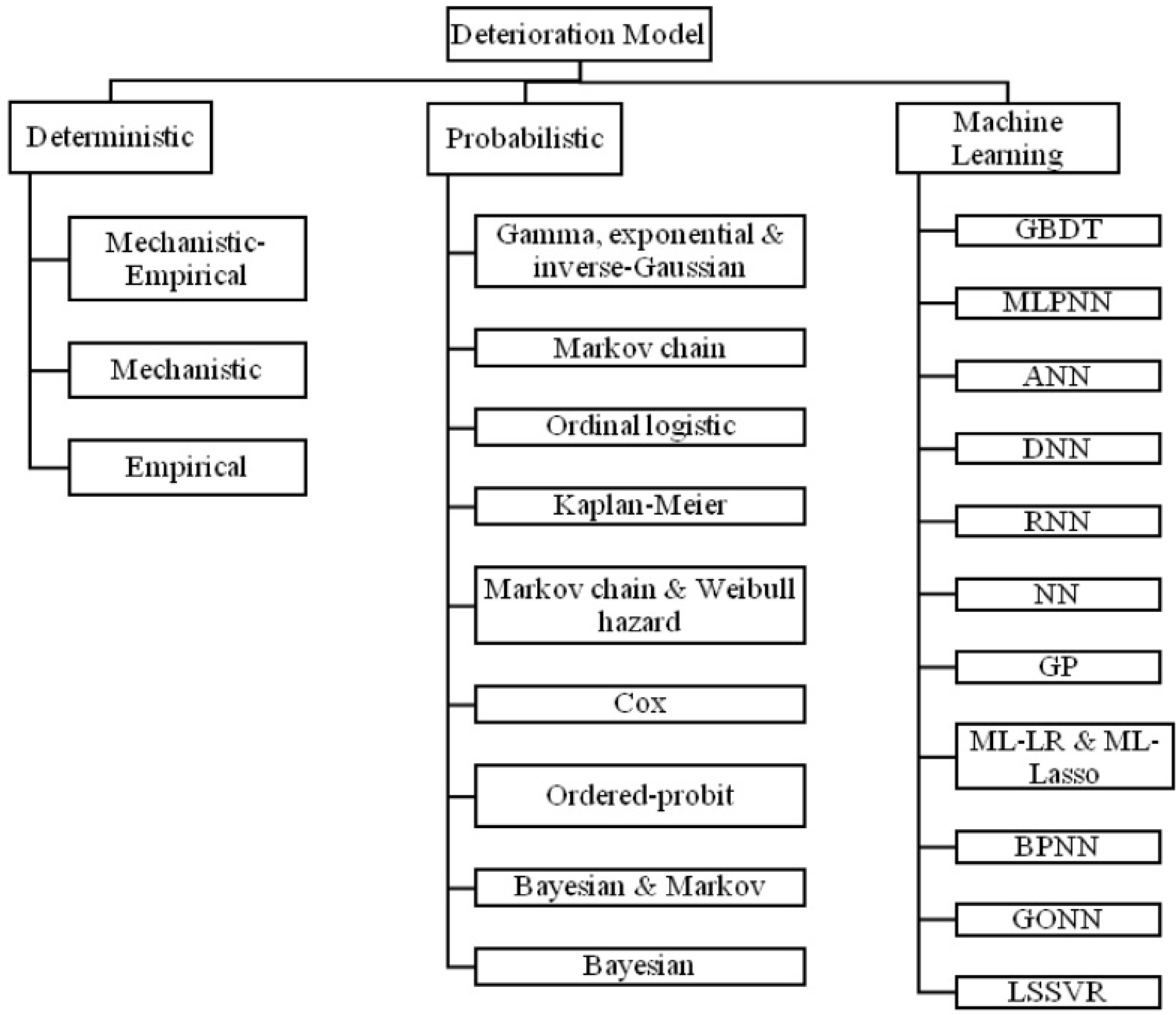
Figure 3.
Classification of reviewed prediction models. ANN: Artificial Neural Network, BPNN: Back Propagation Neural Network, DNN: Deep Neural Network, GBDT: Gradient Boostine Decision Tree, GONN: Genetically Optimized Neural Network, GP: Genetic Programming, LSSVR: Least Squares Support Vector Regression, ML-Lasso: Machine Leaming regularzed regression with Lasso, ML-LR: Machine Leaming Liear Regression, MLPNN: Machine Leaming Propagation Neural Network, RNN: Recurrent Neural Network.
Deterministic models
-
The condition of a pavement is impacted by multiple factors. One such factor is pavement roughness, which serves as an indicator for assessing pavement quality. Various elements influence pavement roughness, including initial roughness, pavement age, climatic variables, structural characteristics of the pavement, traffic load, subgrade specifications, drainage type, drainage condition, as well as past treatment and maintenance activities[25−31]. Deterministic models are extensively employed by transportation agencies to establish a connection between pavement condition and contributing deterioration factors. These models are preferred due to their simplicity and user-friendliness. Pavement deterministic models are typically classified into three groups: mechanistic, empirical, and mechanistic-empirical.
Condition prediction using a mechanistic approach is based on the mechanical and structural characteristics of pavements[24]. Mechanistic models assess the condition of assets by analysing mechanistic responses, such as stresses, strains, and deflections. For example, the load exerted by vehicle wheels is used to estimate the stresses and strains within a pavement layer. These estimations are then incorporated into mechanistic functions to quantify condition values[32,33]. Mechanistic models provide in-depth understanding of the relationship between mechanical responses and the condition of an asset. However, ensuring the accuracy of results from these models is challenging because it requires accounting for numerous parameters that can potentially impact the asset's condition[23].
Empirical methods utilize statistical analysis and take into account significant factors that contribute to deterioration, such as pavement age and traffic load[24]. Empirical methods often employ linear and non-linear regression. The regression analysis performed with a single variable is referred to as univariable regression, while using multiple variables is known as multivariable regression. Since multiple factors can affect the degradation of assets, univariable regression techniques often fail to produce accurate results.
Mechanistic-empirical procedures combine mechanistic functions with historical observations to create prediction models. By using mechanistic methods, these models establish the functional forms and descriptive variables required for accurate predictions[23,24]. These models are typically implemented at the project level and are less commonly used at the network level. Nevertheless, they can be applied in a wider range of situations compared to empirical methods[34]. However, it is important to note that calibration is a crucial step in ensuring the validity of these models across different scenarios[24]. The primary challenge associated with mechanistic-empirical models is the lack of adequate structural data necessary for their application.
Table 1 illustrates the summary of reviewed papers that utilized deterministic models for prediction of the pavement condition.
Table 1. Summary of deterministic prediction models in the reviewed papers.
Reference Pavement types Findings Approach Ramadan & Beckedahl, 2017[35] Asphalt Highlights discrepancies between lab and real-world asphalt pavement performance. Evolving properties due to traffic and environment pose challenges. Current methods fall short. A new incremental approach is proposed, addressing material variations over time. Mechanistic Norouzi et al, 2017[36] Asphalt Development of a Layered Viscoelastic Critical Distresses (LVECD) model to predict fatigue performance. This study applied the LVECD program to 18 pavements in the US and Canada. Comparing simulations with field observations, the study found strong agreement in fatigue damage trends, validating LVECD's accuracy in predicting crack initiation and propagation. Shah et al., 2013[37] Flexible pavements Overall Pavement Condition Index (OPCI) for a selected network of urban roads in Noida city (India). Four key performance indices were calculated, including distress, roughness, structural capacity, and skid resistance. By combining these indices, the OPCI was created, offering a reliable indicator of pavement condition. Albuquerque et al., 2022[38] Flexible pavements Urban Pavement Condition Index (UPCI) was developed using multiple regression with pavement defects and Current Serviceability Value (CSV). The UPCI was compared with other PCIs, showing variability and analyzed through statistical tests. Empirical Al-Suleiman et al., 2020[39] Flexible pavements Relationship between maintenance costs and pavement deterioration rate studying 1.5 years' data to understand the link between maintenance costs and pavement deterioration Joni et al., 2020[40] Flexible pavements Strong model for predicting pavement roughness (IRI) based on visible pavement distress data from 83 flexible pavement sections. Factors such as polished aggregate, potholes, alligator cracking, patching, raveling, and corrugation were considered. The model, created through stepwise multiple linear regression in SPSS. Harikeerthan et al., 2020[41] Flexible pavements Developed Pavement Deterioration Models and a Relative Deterioration Index using data from Automated and Manual Field Evaluation methods on Bangalore city roads (India). Findings highlighted the dominant impact of roughness on road deterioration in selected categories. Alaswadko et al., 2019[42] Sealed granular pavements Developed robust multilevel roughness models for sealed granular pavements using data from 40 highways (2300 km). Key predictors included traffic loading, subgrade soil potential, climate, drainage, and initial pavement strength. Time was the most significant predictor, followed by initial pavement strength and traffic loading. Mamlouk et al., 2018[43] Flexible pavements Relationship between pavement ride quality (roughness) and rut depth and accident rate on highways. Found that the accident rate remained stable until pavement roughness exceeded 210 inches/mile or rut depth reached 0.4 inches. Beyond these thresholds, the crash rate increased significantly. Hassan et al., 2017[44] Chip/spray seal, Geotextile seal, Stone mastic asphalt, Open graded asphalt,
Ultra-thin asphaltEnhancing the identification and prioritization of resurfacing needs through comparative analysis of deterioration models for five types of bituminous surfaces. Surface condition data, transformed into Surface Inspection Rating (SIR), was analyzed using regression, logistic regression, and Markov chains. Results showed similar predictions and deterioration rates across the approaches for most surfacing types. Sylvestre et al., 2019[45] Flexible pavements Incorporating frost heave in long-term roughness performance prediction models. The result presented illustrate that a significant increase in long-term IRI deterioration rate, usually caused by a more variable subgrade soil, is likely to contribute to the rehabilitation of the pavements up to four years before the end of the pavement service life. Wang et al., 2017[23] Jointed plain concrete pavement (JPCP) Comparative analysis of multivariate non-linear regression, artificial neural network and Markov chain models for faulting-based pavement performance prediction. MNLR needs recalibration, ANN requires more data, and MC, though promising for limited data, lacks quantitative correlation. Future research should blend model strengths for improved accuracy. Sultana et al., 2016[46] Flexible pavements Examined flood-affected roads' data and proposed a model showing rapid post-flood pavement deterioration. Findings align with observations post-Hurricanes Katrina and Rita in New Orleans (US). Ziari et al., 2016[47] Flexible pavements Comparative analysis of group method of data handling and ANN in terms of their capabilities. Nine input variables were studied, focusing on traffic, environmental changes, and pavement structures, with IRI. Results showed that ANNs accurately predicted pavement condition in short and long terms, while Group Method of Data Handling (GMDH) models did not achieve acceptable accuracy. Luo, 2014[48] Flexible pavements Predictive models and a composite distress index for pavement management and preservation projects. Using MLR and ANN models, the research recommends MLR models due to their simplicity and robust performance. An Analytic Hierarchy Process (AHP) was utilized to create a composite distress index, helping Kentucky Transportation Cabinet (KYTC) prioritize projects based on 11 distress indices. Shahini et al., 2014[49] Flexible pavements Integrating the impact of severe events like snow storms and floods on road infrastructures achieving over 90% accuracy using LTPP and National Oceanic and Atmospheric Administration (NOAA) data. Sreedevi et al., 2014[4] Flexible pavements Maintenance Priority Index (MPI) for six sections of State Highway SH-1, considering factors like pavement condition, riding quality, traffic, and land use. Significant relationships between pavement distress and roughness were established using MLR. Anyala et al., 2014[24] Asphalt Predictive model considering climate, traffic, materials, and pavement design factors to assess the impact of climate change on road pavement rutting. Developed using Bayesian regression and Monte Carlo simulations, the model provides probabilistic estimates for rut depth progression and maintenance costs. Prasad et al., 2013[50] Rural Roads
(Flexible Pavement)Relationship between pavement roughness and surface distresses focusing on roughness and its relation to safety and driving ease using IRI to measure roughness. Bump Integrator, calibrated with MERLIN, collected roughness data. Owolabi et al., 2012[51] Flexible pavements Pavement performance models for Nigeria (Africa) and similar developing countries to predict deterioration rates. Key parameters affecting Pavement Condition Score (PCS) and IRI were identified using Stepwise Regression. Depth of ruts and area of potholes impacted PCS, while number of patches, length of cracks, and depth of ruts affected IRI. Chen & Zhang, 2011[52] Asphalt Exploring the suitability of four IRI-based deterministic deterioration prediction models including the NCHRP and Dubai models, using NMDOT PMS and LTPP data in New Mexico (US). NCHRP and Dubai models prove effective, while Al-Omari—Darter and NMDOT models lack statistical reliability. Additionally, a survival curve probabilistic model for pavement service life prediction is introduced, with traffic loading approach yielding the most accurate results. Sidess et al., 2022[53] Flexible pavements Predictive model for IRI deterioration, calibrated using pavement structural factors like structural number, asphalt thickness, subgrade strength, and environmental conditions. Results, compared with road measurements in diverse climate zones managed by Netivei Israel (NETI), exhibit strong correlation. Mechanistic-Empirical Gupta, 2019[54] Rural Hilly Roads Development of Rural Road Maintenance Priority Index (RRMPI) for rural road networks in hilly terrain areas of India on a scale of 0-100, which efficiently assesses pavement conditions. RRMPI was used to select maintenance strategies for 12 rural road stretches in Himachal Pradesh, ensuring cost-effective and targeted maintenance efforts. Katicha et al., 2016[55] Flexible pavements Considering pavement age and Modified Structural Index (MSI) and accurately predicts average critical condition index of pavement sections. The model with MSI was 50,000 times more accurate. Lowering MSI from 1 to 0.6 for a 7-year-old pavement reduced the Critical Condition Index (CCI) from 79 to 70. Hasan et al., 2016[56] Flexible pavements Compared empirical and mechanistic-empirical approaches in flexible pavement design across 76 locations in 13 US states. Findings revealed significant impacts of mean annual temperature and precipitation on various pavement distresses, except for the IRI, which remained unaffected. Jung & Zollinger, 2011[57] Jointed plain concrete pavement Faulting model calibrated using a erosion test involving the Hamburg wheel-tracking device and Long-Term Pavement Performance (LTPP) data. The review found that people often use empirical methods to predict pavement conditions in the future. However, these methods can be limited because there isn't always enough data. Also, they often only look at a few important factors in the road's deterioration because of data issues or limitations in their analysis. Another problem is that the equations used to describe how these factors affect the road condition can be really complicated[58].
Mechanistic and mechanistic-empirical performance models can predict pavement performance. Although these models require more data for calibration, they offer useful simplifications compared to other prediction models such as empirical models[59]. However, the process of selecting suitable prediction equations holds great importance in the development of an optimal performance model[60]. Creating empirical models requires a sizable dataset with pavement conditions and clear mathematical and physical boundaries identification. These steps are vital for precise modelling and to avoid substantial errors[61].
Regression models provide a straightforward approach for analysis, allowing the utilization of various equations. The effectiveness of the assumed functions or equations in constructing regression models can be assessed using statistical metrics, aiding in the evaluation of their capacity to accurately conform to observed data[62]. While the coefficient of determination is a widely employed metric for appraising predictive models, some researchers contend that alternative statistical measures rooted in error percentages can also be applied to gauge the quality of fit[62−64].
Probabilistic models
-
By utilizing the probability concept, these models estimate the likelihood of an asset's future condition or life expectancy, either as a range of potential outcomes or a specific probability value[32,65]. These models provide a more comprehensive understanding of risks and can assist asset managers in mitigating risks associated with their decision-making[22,66].
Markov chain algorithms utilize the stochastic concept of the Markov process, which calculates the probability of each potential event in a sequence based on its likelihood. The probability of an event is influenced solely by the preceding event's state. By examining the transition of an asset item's condition between two consecutive inspections, a transition matrix is created. This matrix is then used to predict future condition values[67].
Distribution models serve the purpose of predicting an asset's future state and its associated likelihood by employing a predefined probability distribution. Nevertheless, when the available data is insufficient, these models must make simplifications and select a probability distribution, which can introduce inaccuracies since the chosen distribution might not perfectly align with the real-world data. Commonly utilized probability distribution models include Weibull, Markov-Weibull, Kaplan-Meier, and Bayesian. The Weibull-based analysis involves modelling an asset item's survival time distribution using the Weibull probability distribution. In the Markov-Weibull approach, it combines the Markov transition matrix with the Weibull survival distribution to predict future condition possibilities. Bayesian analysis, on the other hand, incorporates prior knowledge of condition measurements along with information gathered from historical observations to construct a probabilistic predictive model[22,23,68].
Table 2 illustrates the summary of reviewed papers that utilized probabilistic prediction models. After conducting a review, it was found that the Markov chain is the most commonly used probabilistic method for predicting pavement performance.
Table 2. Summary of probabilistic prediction models in the reviewed papers.
Reference Pavement types Findings Approach Pantuso et al., 2021[69] Flexible pavements Improve prediction accuracy by combining the model's degradation estimate with real-world observations using negative binomial regression based on pavement age. Various road type models were compared with traditional methods, and the linear empirical. Results showed substantial improvements, reducing mean square error by 33% (interstate), 36% (primary), and 41% (secondary roads) compared to measured conditions without additional modeling. Bayesian Issa& Abu Eisheh, 2019[70] Flexible pavements Create a predictive model for pavement condition to optimize road maintenance and rehabilitation plans. By assessing pavement sections visually and using the Pavement Condition Index (PCI), the study suggests early prediction (within 5-10 years) enables cost-effective preventive maintenance actions, like crack sealing and overlay, optimizing limited budgets for road maintenance. Markov chain Gursoy, 2019[71] General Develop network-level pavement deterioration prediction models in the absence of key input variables like traffic loading, freeze-thaw cycles, snow plowing, construction quality, pavement thickness, and age. Markov chain Rose et al., 2018[72] Low volume roads Include uncertainties in low-volume road pavement behavior that deterministic models overlook. Focused on distresses like raveling, potholes, and edge failures. Rare load-associated distresses indicated drainage and construction quality issues as main deterioration causes. The study analyzed distress progression with age and established probabilities for distress occurrences. Gamma, exponential & inverse-Gaussian Soncim et al., 2018[73] Asphalt Suggest a method to predict IRI when historical pavement condition data is lacking. Transition probability matrices, incorporating factors like traffic density and climate, were established. The models, based on the International Roughness Index, highlighted variations in pavement behavior tied to factors such as traffic and climate, as per expert experiences. Markov chain Saha et al., 2017[74] General Enhance Colorado DOT's deterioration prediction methods by factoring in degradation process uncertainties alongside deterministic techniques. Longitudinal, fatigue, and rut indices deteriorated slowly, while transverse and ride indices showed faster deterioration. The models achieved high accuracy (R2 > 0.84). Markov chain Abaza, 2017[75] Rehabilitated pavement Introduces two empirical Markovian models for predicting transition probabilities in rehabilitated pavements: one for staged-homogeneous transitions and another for non-homogeneous transitions. These models calculate deterioration probabilities based on original pavement data and adjust for increased traffic loads and decreased pavement strength. Markov chain Abaza, 2016[76] Flexible pavements Simplified Markov model predicted future pavement conditions efficiently by dividing the analysis period into staged-time periods. Deterioration probabilities, influenced by increasing traffic and pavement degradation, were estimated using C constants, determined through a trial-and-error approach. Markov chain Moghaddass et al., 2015[77] General Predicting remaining useful life in mechanical systems, vital for cost-effective maintenance which focuses on multistate degradation, common in real-world scenarios. Addressing interval-censored data at fixed inspection points, the research develops accurate methods for parameter estimation and essential reliability measures. Markov chain D. Chen et al., 2014[78] Flexible pavements Developed a precise data cleansing method for pavement condition data and established the superiority of the sigmoidal model in predicting pavement performance. It introduced an innovative approach for constructing piecewise linear distress models. Despite a reduced dataset, the study met analytical requirements due to meticulous data merging. Ordinal logistic Khan et al., 2014[79] General Discusses various methods, including non-homogeneous transition probability matrices, for deriving Road Deterioration (RD) models. The study presents new RD models considering flooding effects and optimal Maintenance (M) and Rehabilitation (R) strategies. Markov chain Anyala et al., 2014[24] General Predictive model considering climate, traffic, materials, and pavement design factors to assess the impact of climate change on road pavement rutting. Developed using Bayesian regression and Monte Carlo simulations, the model provides probabilistic estimates for rut depth progression and maintenance costs. Bayesian Thomas &Sobanjo, 2013[80] Flexible pavements Presents a flexible semi-Markov model for pavement deterioration, utilizing Weibull distribution for condition state durations which accommodates non-exponential durations. Monte Carlo simulations reveal the semi-Markov model's superiority in capturing actual flexible pavement deterioration patterns compared to the Markov model in specific cases Markov chain Gao et al., 2012[81] Flexible pavements Include a random term in the hazard function to enhance fatigue cracking estimates by accounting for unobserved variations. The model's efficiency is demonstrated using the LTPP database. Bayesian C. Chen & Zhang, 2011[52] General Exploring the suitability of four IRI-based deterministic deterioration prediction models including the NCHRP and Dubai models, using NMDOT PMS and LTPP data in New Mexico (US). NCHRP and Dubai models prove effective, while Al-Omari—Darter and NMDOT models lack statistical reliability. Additionally, a survival curve probabilistic model for pavement service life prediction is introduced, with traffic loading approach yielding the most accurate results. Kaplan-Meier Abaza, 2011[82] Flexible pavements Stochastic approach to estimate flexible pavement thickness, integrating traditional and stochastic factors, notably initial and terminal transition probabilities. A discrete-time Markov model used these probabilities to predict pavement distress ratings. Empirical models for low volume roads were developed, considering relevant design factors and employing indicators like the area under the performance curve and average distress rating. Markov chain Kobayashi et al., 2010[83] General Method for predicting road section deterioration using Markov transition probability models and hazard models. Road states are categorized into ranks, and deterioration processes are analyzed through exponential hazard models, considering non-uniform inspection intervals. Markov chain & Weibull hazard Abaza et al. 2009[84] General Predict pavement remaining strength by adjusting initial strength using layer capacity factors. Initial strength is determined by indicators like gravel equivalent or structural number. Markov chain Pulugurta et al., 2009[85] General Markov prediction model using ODOT's pavement condition database in which transition matrices were modified through imputation techniques. Markov chain Abaza et al., 2007[86] General Predicts pavement conditions using initial and transition probabilities which creates long-term restoration plans balancing performance and budget. Markov chain Ortiz-García et al., 2006[87] General Three methods, based on historical data, regression curves, and yearly condition distributions. Despite minor deviations, the third method consistently produced distributions similar to the original data. Empirical and Markov chain Yang et al., 2005[88] General Dynamic Markov chain approach, incorporating a logistic model for explicit transition probabilities. By capturing crack state transitions and randomness, it provides a more suitable and efficient method for pavement deterioration modeling. Markov chain Shahin, 2005[89] General Practical guidance for cost-effective pavement management, covering project and network-level strategies, cost analysis, equipment selection, and rehabilitation techniques with a focus on the PCI procedure. Markov chain Abaza, 2005[90] Flexible Pavement Overlay design models for flexible pavements by assessing surface conditions over time. Performance curves link surface condition to service life or load applications, allowing compensation for performance loss. Markov chain Abaza et al., 2003[91] Flexible Pavement Approach to flexible pavement design has been developed, considering anticipated performance and life-cycle cost. By optimizing the terminal serviceability index, this method ensures cost-effective designs, challenging existing AASHTO recommendations. Markov chain Hong et al., 2003[92] General Novel probabilistic approach for predicting pavement performance, considering uncertainties in traffic, environment, material properties, and pavement geometry whish aligns well with established pavement deterioration models (OPAC and AASHTO). Markov chain Ferreira et al., 2002[93] General Cost-effective pavement management model using deterministic performance estimates for cracking, rutting, disintegration, and roughness. The approach employs a modified PSI and genetic algorithms for optimization. Genetic algorithm Mishalani et al., 2002[94] General Alternative approach using probabilistic duration models to capture condition evolution over time. The method estimates state transition probabilities from these duration models, addressing the shortcomings of existing techniques. Markov chain Ferreira et al., 1999[95] General Detailed comparison of numerous pavement performance models such as regression analysis, Bayesian methodology, Markov process, nonhomogeneous Markov process, and semi-Markov process. Regression, Markov, Semi-Markov, Bayesian Li et al., 1996[96] General Method for accurate pavement deterioration prediction, vital for repair planning using advanced techniques, avoiding subjective opinions or extensive data and calculates transition probability matrices and pavement condition probabilities for various stages. Markov chain Madanat et al., 1995[97] General Robust econometric method based on ordered probit techniques to estimate infrastructure deterioration models and transition probabilities from condition rating data which treats facility deterioration as a latent variable, addresses the discrete nature of condition ratings, and explicitly links deterioration to relevant variables, Markov chain Wang et al., 1994[98] General Refined Network Optimization System (NOS) by developing new matrices using current data and employing the Chapman-Kolmogorov method to establish long-term pavement behavior. The modified matrices, incorporating accessibility rules, enhanced prediction accuracy. Markov-process-based transition Butt et al. 1987[99] General Pavement Condition Index (PCI) and age-based model, dividing PCI into ten states over 6-year. Transition matrices, determined through nonlinear programming, enable accurate prediction. Markov chain Golabi et al. 1982[100] General PMS to produce optimal maintenance policies. The model integrates management policy decisions, budgetary policies, environmental factors, and engineering decisions. Markov chain Karan et al. 1976[101] General Method to prioritize urban pavement improvements which outlines a management framework and introduces a serviceability performance concept validated through street testing. The study suggests criteria for necessary improvements, a performance prediction method, and a network priority programming scheme for urban pavements. Markov chain The Markov chain model is commonly used to predict condition values, especially when there isn't enough data for all contributing factors. This model focuses on transition probabilities and the reasons behind these transitions, using historical data from roadways' operation and maintenance. In the literature, Markov chain models are divided into two types: homogeneous and non-homogeneous. Homogeneous models assume that an asset's condition at a specific time only depends on its previous condition, and transition probabilities remain constant over time. However, these assumptions can lead to prediction inaccuracies. Non-homogeneous models, on the other hand, consider different transition probabilities at different times, taking all previous stages into account when forecasting an asset's future condition. Still, some studies have found inaccuracies in the results of non-homogeneous models[102].
Deterministic and probabilistic methods are ways of figuring out how things are connected. But sometimes, to make it easier, we simplify things too much. These methods rely on personal guesses and making things simpler when trying to find patterns. The deterministic way has often been too narrow because it only looks at a few things that make something get worse. This is because we don't always have all the information, and we don't fully understand why things get worse. So, these methods might not work well in all situations. Also, when experts use deterministic methods, their personal opinions can affect the results, making them less accurate. Some studies have tried to fix this by combining personal opinions with math, but the problem of simplifying things too much still exists[103].
Machine learning models
-
Machine learning, first proposed by Arthur Samuel in 1959, is about computers learning and improving their performance through experience, without needing detailed programming for each task. Recently, researchers have shown increasing interest in using machine learning to predict maintenance tasks[104]. Machine learning methods delve into complex data relationships and patterns with little human involvement. These methods learn from data, improving predictive accuracy without relying on subjective assumptions. This has sparked growing interest among researchers in using machine learning to predict maintenance tasks. Artificial Neural Networks (ANNs) are a prominent machine learning tool in highway asset management. Yet, ANN has drawbacks, such as lengthy training and the risk of getting stuck in local minimum points during training. Additionally, selecting the right neural network structure and training algorithms can be challenging when building an ANN model[23].
Table 3 illustrates the summary of reviewed papers that utilized machine learning prediction models. After reviewing existing literature on machine learning models for predicting pavement conditions, it was discovered that most studies predominantly employed ANNs.
Table 3. Summary of machine learning prediction models in the reviewed papers.
Reference Pavement types Findings Approach Guo et al., 2022[105] Asphalt Enhance pavement performance estimation, offering a dependable maintenance reference. GBDT Alatoom& Al-Suleiman, 2022[106] Asphalt ANN models outperform regression models in accurately predicting IRI. ANN Haddad et al., 2022[107] Flexible pavements Predictive rutting curves to estimate road deformations based on traffic, climate, and performance factors. DNN Issa et al., 2022[108] General A cost-effective model utilizing machine learning techniques was developed to assess Palestinian pavement conditions. Traditional visual inspections were replaced with a hybrid model, combining classical machine learning and neural networks. ANN Sudhan et al., 2020[109] Flexible pavements Pavement deterioration prediction models for low-volume roads in Kerala, India, using system dynamics and Powersim Studio version 10. Fourteen roads were analyzed, and the models were validated against field data. Results show that system dynamics is effective for developing accurate pavement deterioration prediction models. Powersim Studio Choi & Do, 2020[110] Flexible pavements An algorithm was developed to predict the condition of road sections for a year based on time series data. Optimized sequence lengths reduced errors by 58.3-68.2%, achieving high prediction accuracy (0.71-0.87). RNN Hussan et al., 2019[111] Asphalt Non-linear regression and artificial neural networks effectively modeled permanent strain, with temperature as the most significant factor. ANN outperformed regression, accurately predicting strain for SP-B graded mixtures (R2 = 0.99) and showing high overall prediction performance. ANN Rezaei-Tarahomi et al., 2019[112] Rigid airfield
pavementsCompared critical tensile stresses predicted by ANNs with 3D-FE solutions for large aircraft which demonstrated that ANNs accurately assessed top-down critical tensile stress sensitivity, suggesting their potential for airport pavement failure analysis. MLPNN Yao et al., 2019[113] Asphalt Models to predict pavement deterioration (rutting, roughness, skid-resistance, transverse cracking, and surface distress) achieving an average testing R-square of 0.8692. Traffic loads affected skid-resistance and transverse cracking, while pavement treatments had a high impact on crack prediction models. NN Chopra et al., 2018[114] Flexible pavements Genetic Programming (GP) models to predict pavement distress on urban roads in Patiala City, Punjab, India. These models accurately forecasted cracking, raveling, pothole, rutting, and roughness progression using data from 16 roads collected between 2012 and 2015. GP Okuda et al., 2017[115] General Method to predict rutting depth using NN and applied dropout and gradient clipping techniques to enhance accuracy. Compared to MLR and Multi-Layer Perceptron (MLP), RNN showed superior prediction ability, with lower RMSE and higher correlation coefficient (R) with measured values RNN Marcelino et al., 2017[116] Asphalt Used scikit-learn, a Python machine learning library, to predict asphalt pavement friction using data from 113 sections of asphalt concrete pavement across the US. Two machine learning models were developed, showing similar performance. The research emphasized the significance of initial friction in the evolution of friction over time. ML-LR &ML-Lasso Hamdi et al., 2017[117] Flexible pavements Creating an ANN model for SDI prediction based on parameters like crack area, crack width, pothole, rutting, patching, and depression. The model, applied to Integrated Road Management System (IRMS) data, achieved a high correlation (R2 = 0.996%). Rutting (59.8%), crack width (29.9%), and crack area (5.0%) were identified as the most influential parameters. ANN Sanabria et al., 2017[22] Flexible pavements Compared Probabilistic Neural Networks Model (PNNM) and Ordered-Probit Models (OPM) using traffic data in which PNNM proved more accurate, identifying peak hour volume and single heavy commercial average volume as significant predictors. ANN Amin & Amador-Jiménez, 2017[118] Flexible and rigid pavements Applied a Backpropagation Neural (BPN) network to improve PCI predictions for Montreal City's roads. Key factors like AADT, ESALs, Structural Number (SN), pavement age, slab thickness, and ΔPCI were considered. BPNN Ziari et al., 2016[119] General Explores Support Vector Machine (SVM) methods to predict pavement condition using five kernels and nine input variables. Results demonstrate the effectiveness of the Pearson VII Universal kernel in accurately forecasting pavement performance over its life cycle. SVM Karlaftis & Badr, 2015[120] Asphalt Used a genetically optimized Neural Network model to accurately predict alligator crack initiation following pavement treatments. Utilizing data from LTPP and SPS-5, the approach established links between external factors and cracking probability. ANN Kargah-Ostadi & Stoffels, 2015[121] Asphalt Creating a framework to compare pavement performance modeling techniques and improving parameterization robustness, comparing machine-learning techniques using Federal Highway Administration data. Key principles were considered, and models like artificial neural networks and support vector machines were tested. ANN Sirvio & Hollmén, 2014[122] General Comparing three prediction model for road condition.
Least Squares Support Vector Regression outperforms Radial Basis Function networks and multiple linear regression, demonstrating superior accuracy in road condition predictions.LSSVR Lee et al., 2014[123] Flexible pavements Three ANN models were developed using deflection databases. The model considering all key parameters proved most accurate and required less training time. Complex models didn't improve results significantly. Integrating engineering and statistical knowledge led to accurate predictions, minimizing time and effort. ANN Chandra et al., 2013[124] Flexible pavements Nonlinear regression models are outperformed by ANNs in predicting pavement roughness. The ANN model shows 18% lower Mean Absolute Error (MAE) than the linear model and 11% lower than the nonlinear model, demonstrating its superior forecasting capability based on distress parameters. ANN Bosurgi et al., 2007[125] General Showcased the effectiveness of a neural network-based Sideway Force Coefficient (SFC) prediction model for an Italian motorway, proving its superiority over traditional linear regression methods in analyzing road problems. ANN Yang et al., 2003[126] Flexible pavements ANN models to forecast pavement conditions like crack rating, ride rating, and rut rating. These models, based on Florida Department of Transportation data, accurately predict pavement conditions for up to five years. ANN Huang et al., 1997[127] General Assessed pavement condition prediction in Kansas Department of Transportation's (KDOT) system using multiple regression and ANN. ANNs proved more effective due to the binary nature of the data, outperforming multiple regression methods. ANN ANN: Artificial Neural Network, BPNN: Back Propagation Neural Network, DNN: DeepNeural Network, GBDT: Gradient Boosting Decision Tree, GONN: Genetically Optimized Neural Network, GP: Genetic Programming, LSSVR: Least Squares Support Vector Regression, ML-Lasso: Machine Learning regularized regression with Lasso, ML-LR: Machine Learning Linear Regression, MLPNN: Machine Learning Propagation Neural Network, RNN: Recurrent Neural Network. Neural network models for predicting pavement performance have certain limitations, such as the requirement for data related to traffic levels, climate conditions, and other pavement condition indicators in the long term[128]. A significant drawback of utilizing neural network models for pavement performance prediction is the necessity for numerical verification and statistical tests to validate the accuracy of the models, especially for artificial neural networks and neuro-fuzzy models. Additionally, obtaining pavement condition data, particularly data related to Pavement Condition Index (PCI), poses a challenge for model developers. Furthermore, finding a suitable flexible pavement with complete service life information can also be difficult[119]. Since the 1990s, ANNs have been extensively used as a machine-learning algorithm for predicting the condition or life expectancy of highway assets. However, selecting appropriate training algorithms and finding the optimal model architecture can be challenging. Additionally, the performance of traditional ANNs can be limited by the time-consuming training process and the instability of the model in local minimum points[23,129].
Comparison between deterministic, probabilistic, and machine learning models
-
In summary, each prediction model has its specific features, strengths, and limitations. Therefore, choosing an appropriate prediction model is crucial for developing a high-quality prediction performance system.
The paper is focused on the input/output of deterministic, probabilistic, and machine learning pavement performance prediction approaches. Furthermore, comparison between the pavement performance models in terms of the advantages, disadvantages, and potential applications is presented in Table 4.
Table 4. Comparison between deterministic, probabilistic, and machine learning models.
Models Advantages Disadvantages Potential applications Deterministic models • User-friendly and straightforward
• Uses well-defined equations and models, making them transparent and understandable
• Utilizes material properties closely tied to real pavement performance
• Offers dependable performance forecasts
• Considers environmental factors, varying loads, and material aging effects
• Yields highly accurate predictions when the conditions, materials, and loads are well-known
• Provide insights into which factors contribute to pavement performance
• Generally stable and do not rely on probabilistic assumptions• Limited to predicting performance within its specific development setting
• Offers an impractical estimation for long-term performance prediction
• Solely relies on the mechanics of materials theory for predictions
• Sensitive to the quality and accuracy of the input data, and minor errors in material properties, traffic loads, or environmental factors can lead to inaccurate predictions
• Hardly accounts for real-world conditions which are often subject to significant variability that can lead to conservative predictions.
• Often simplify or ignore complex interactions between different factors affecting pavement performance
• Are inflexible and do not adapt well to changing conditions• Useful in the initial design phase of pavements, especially when the conditions and loads are well-understood
• Valuable for quality control during pavement construction
• Can assist in planning maintenance and rehabilitation activities based on the predicted deterioration rate
• Provides a clear way to illustrate the fundamental mechanics of pavement behavior
• Suitable for predicting pavement performance on simple road networks or specific sections of roads with constant traffic loads and materialsProbabilistic models • Well-suited to handle the inherent variability in pavement performance due to factors such as traffic loads, material properties, and environmental conditions
• Allows for quantifying risks associated with pavement performance which is valuable for decision-makers in understanding the likelihood of different performance outcomes
• They can adapt to different scenarios and changing conditions, making them suitable for a wide range of pavement types and locations
• Can effectively integrate data from various sources, including historical performance data, material testing, and environmental monitoring, to improve predictions• Often more complex than deterministic models, requiring advanced statistical and mathematical techniques
• A significant amount of data is often needed to build reliable models
• Outputs of models may be less intuitive for non-technical stakeholders due to their reliance on statistical distributions and probabilities
• Models require extensive computational resources, which can be a limitation for some applications, especially when real-time predictions are needed• Models are crucial for asset management in pavement networks helping to prioritize maintenance and rehabilitation efforts based on the likelihood of pavement distress and performance degradation.
• Models can be used for life-cycle cost analysis, allowing agencies to evaluate the cost-effectiveness of different pavement design and maintenance strategies over the long term
• Can be used to develop performance-based specifications that set performance targets meeting the specific performance criteria
• Models can help in assessing the vulnerability of pavements and plan for adaptation strategies based on probabilistic scenarios in environmental conditions
• Used in research to better understand the uncertainties and variability associated with pavement performanceMachine learning models • Uncovers complex, data-driven patterns and relationships that might not be captured by traditional analytical methods and can lead to more accurate predictions.
• Adapts changing conditions and continuously improve their predictions as new data becomes available
• Effectively handles and integrates various types of data, including sensor data, images, and textual information, providing a holistic view of pavement performance
• Models can be trained, hence can automate the prediction process, reducing the need for manual intervention and potentially saving time and resources
• Can scale to handle large datasets and can be used for predicting performance across entire pavement networks• Require a substantial amount of high-quality training data, and the availability and quality of such data can be a limiting factor for their application
• Some machine learning algorithms can be complex and difficult to interpret
• Models are prone to overfitting, where they perform well on training data but generalize poorly to new, unseen data
• Developing and fine-tuning machine learning models can be time-consuming and resource-intensive, requiring expertise in data science and machine learning
• Models often lack a direct physical understanding of the underlying pavement mechanics, which may limit their utility for some engineering applications• Predicts the timing and type of maintenance or repair needed for specific pavement sections based on data such as distress measurements, traffic loads, and environmental conditions
• Forecasts the future condition and performance of pavements, helping agencies plan and budget for maintenance and rehabilitation activities
• Can be used to optimize pavement designs by analyzing various design parameters and their impact on performance, leading to cost-effective design decisions.
• Quantifies the risks associated with different pavement scenarios, helping agencies make informed decisions about asset management and funding allocation
• Assesses the environmental impact of pavements, including energy consumption, emissions, and sustainability, by considering various design and maintenance strategies
• Processes a real-time sensor data to monitor pavement performance, detect distress early, and trigger maintenance actions when necessaryMarkovian-based models are a valuable tool in pavement management systems when historical data is available. Moreover, it is useful when a simplified probabilistic approach to pavement performance prediction is sufficient for decision-making. Markovian-based models are found extensively being used for pavement performance prediction in asset management systems to predict when maintenance or rehabilitation is necessary for a pavement section, in allocating budgets for pavement maintenance and rehabilitation projects by estimating which sections are likely to deteriorate in the near future, in assessing the impact of different maintenance and rehabilitation strategies on the long-term condition of pavements and in real-time pavement monitoring systems to assess current and future pavement conditions. However, the choice between deterministic, probabilistic, or machine learning approaches depends on the specific application, the availability of data, the level of uncertainty in the problem, and the desired level of prediction. Often, a hybrid approach that combines elements of these different approaches can provide the most accurate and comprehensive pavement performance predictions.
-
The increase in the number of road users has led to the degradation of pavement surfaces, resulting in safety and comfort issues for road users. Researchers have extensively studied the current state of pavement degradation and made efforts to predict future changes in pavement structure. Pavement Management Systems (PMS) are instrumental in developing performance models that estimate pavement condition and degradation severity over time. Previous studies have focused on creating performance prediction models using various datasets and indices, including the Long-Term Pavement Performance (LTTP) database. Machine learning (ML) algorithms and artificial neural network (ANN) modelling have been widely employed, with researchers generally acknowledging their accuracy in estimating pavement condition considering factors like traffic, pavement age, and weather conditions. Regression models have also exhibited high accuracy in detecting and classifying pavement damages. However, it is important to acknowledge that each prediction model possesses its own strengths and weaknesses. Some models excel in multi-prediction and multi-classification tasks, such as ANN, ML, and RE models. Deterministic models, on the other hand, may have limitations in predicting the actual condition of pavement surfaces. Therefore, selecting an appropriate prediction model is crucial for achieving a high-quality prediction performance system. By considering the specific features, strengths, and weaknesses of each model, researchers and practitioners can make informed decisions in implementing prediction models that best suit their needs. The advancement of prediction models and the integration of innovative technologies will continue to contribute to improved pavement management and the overall safety and comfort of road users.
Furthermore, the prominent aspects missing in the prediction models are extreme climate events and climatic conditions, which have impacts on performance of pavements. Climate change consequences like droughts, floods, temperature changes, wind variations, hurricanes, and freezing-thawing cycles affect roadway assets. Buckling, washed-out shoulders, and pavement cracks become more common due to the climate. Thus, consideration of climatic conditions in prediction models is necessary to improve pavement resilience in further studies of predictive techniques.
-
The authors confirm contribution to the paper as follows: study conception and design: Basnet KS, Shrestha JK, Shrestha RN; data collection: Basnet KS; analysis and interpretation of results: Basnet KS, Shrestha JK; draft manuscript preparation: Basnet KS, Shrestha JK. All authors reviewed the results and approved the final version of the manuscript.
-
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
-
The authors declare that they have no conflict of interest.
- Copyright: © 2023 by the author(s). Published by Maximum Academic Press, Fayetteville, GA. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
-
About this article
Cite this article
Basnet KS, Shrestha JK, Shrestha R. 2023. Pavement performance model for road maintenance and repair planning: a review of predictive techniques. Digital Transportation and Safety 2(4):253−267 doi: 10.48130/DTS-2023-0021
Pavement performance model for road maintenance and repair planning: a review of predictive techniques
- Received: 16 September 2023
- Accepted: 09 November 2023
- Published online: 28 December 2023
Abstract: This paper provides a review of predictive analytics for roads, identifying gaps and limitations in current methodologies. It explores the implications of these limitations on accuracy and application, while also discussing how advanced predictive analytics can address these challenges. The article acknowledges the transformative shift brought about by technological advancements and increased computational capabilities. The degradation of pavement surfaces due to increased road users has resulted in safety and comfort issues. Researchers have conducted studies to assess pavement condition and predict future changes in pavement structure. Pavement Management Systems are crucial in developing prediction performance models that estimate pavement condition and degradation severity over time. Machine learning algorithms, artificial neural networks, and regression models have been used, with strengths and weaknesses. Researchers generally agree on their accuracy in estimating pavement condition considering factors like traffic, pavement age, and weather conditions. However, it is important to carefully select an appropriate prediction model to achieve a high-quality prediction performance system. Understanding the strengths and weaknesses of each model enables informed decisions for implementing prediction models that suit specific needs. The advancement of prediction models, coupled with innovative technologies, will contribute to improved pavement management and the overall safety and comfort of road users.
-
Key words:
- Road Maintenance /
- Prediction Model /
- Deterministic Model /
- Probabilistic Model /
- Machine Learning Model