Loading [MathJax]/jax/output/SVG/jax.js
Search
Submit Manuscript
Advanced Search
MAP  >  Technology in Horticulture
2022 Volume 2
Article Contents
Abstract
Introduction
Materials and methods
Source of liquid whey proteins
Materials
Methods
Preparation of indigenous fruit juices
Preparation of whey protein beverages
Chemical analysis
Microbiological examination
Sensory evaluation
Statistical analysis
Results and dissection
The chemical composition of whey proteins beverages
Microbiological findings of whey proteins beverages
Sensory attributes of whey protein beverages
Conclusions
Author contributions
Data availability
Acknowledgments
Conflict of interest
Supplementary information
Rights and permissions
References
About this article
Next Previous
ARTICLE   Open Access    

Salt tolerance of seven genotypes of zoysiagrass (Zoysia spp.)

  • 1.

    Texas A&M AgriLife Research and Extension Center, 17360 Coit Rd, Dallas, TX 75252, USA

  • 2.

    Biosystems Engineering Department, University of Arizona, 1951 E. Roger Road, Tucson, AZ 85719, USA

  • 3.

    Texas A&M AgriLife Research, 1380 A&M Circle, El Paso, TX 79927, USA

  • 4.

    Department of Agriculture, Collin College, 391 Country Club Road, Wylie, TX 75098, USA

More Information
  • Seven zoysiagrass genotypes were evaluated for salt tolerance in a greenhouse study. The plant materials included Zoysia matrella 'Diamond', Z. japonica 'Palisades', three Z. matrella × Z. japonica hybrids DALZ 1701, DALZ 1713, and 'Innovation', and two Z. minima × Z. matrella hybrids (DALZ 1309 and 'Lazer'). Treatments included a control (nutrient solution) and two saline treatments representing moderate and high salt levels. The electrical conductivity (EC) was 1.3 dS m−1 for control and moderate (EC5) and high salinity (EC10) were 5.0 and 10.0 dS m−1, respectively. At the end of eight-weeks of treatment, the relative (percent control) shoot dry weight (DW) was greatest in 'Diamond' in EC10, and the relative root DW was greatest in DALZ 1309 in EC5. A cluster analysis based on the relative tissue dry weight identified 'Diamond', DALZ 1309, and DALZ 1713 as the most salt tolerant genotypes. Additionally, the green leaf area (GLA) index of 'Diamond' and DALZ 1713 were 98.8% and 100%, respectively, indicating excellent visual appearance under high salt levels. Bi-weekly clipping DW showed that 'Diamond' continued to produce biomass throughout the duration of the study under the EC10 treatment. Sodium (Na+) and chloride (Cl−) content in the shoot tissue of the seven turfgrass genotypes indicated that lower concentrations corresponded to greater salt tolerance indicating exclusion of Na+ and Cl− from the shoot tissue. Taken together, the genotypes 'Diamond' and DALZ 1713 were determined to be the most salt tolerant and recommended for use in areas with high soil or water salinity.

  • Introduction

    Milk proteins are the best protein source because of their essential amino acid score that helps in improving the protein digestibility corrected amino acids scores. The high quality protein content of both whey proteins (20%) and caseins (80%) are satisfying the requirements of human amino acid needs in addition to their digestibility and bioavailability[1].

    Whey proteins are precious watery nutrients as they contain about half of the milk total solids that remain after the caseins are curdled during cheese making, it is a rich source of lactose, whey proteins, some milk salt and water-soluble vitamins[2]. Whey proteins are well-documented as valuable milk ingredients and are highly nutritious food[3]. Moreover, the nutraceutical properties that are derived from the metabolic hydrolysis of milk, its whey proteins, and their peptides include antimicrobial and antioxidant activities[4]. Additionally, the preventive and curative effects that the protein possess have practical applications in the treatment of anemia, liver complaints, and arthritis[5].

    During cheese making, the valuable whey proteins that are lost while separating the whey from the milk[3], could be converted into attractive fermented or non-fermented products for human utilization and consumption[6]. For example, the use of advanced filtration techniques for valorization of whey cheese was found to recover these high value proteins[7,8].

    Baobab (Adansonia digitata L.) is a grossly indigenous fruits[9]. Baobab fruit pulp obtained from the different regions of Sudan were found to contain high vitamin C (358.44 mg/100 g), calcium (393.55 mg/100 g) and phosphorus (91 mg/100 g) levels, in addition to their high protein content (5.2%)[10]. Baobab fruit pulp exhibits higher antioxidant properties[11]. Dry Baobab pulp in Sudan, is either eaten fresh, ground to prepare a refreshing drink, added to gruel during its cooling[10] or as flavor to ice cream[12,13].

    Roselle (Hibiscus sabdariffa L.) belongs to the family Malvaceae, an annual shrub that is grown in many tropical or subtropical countries including Sudan. Moreover, the red calyces of Roselle are usually used for preparing a flavorful and tart beverage either cold or hot to utilize their rich content of the numerous beneficial bioactive compounds[14]. In Sudan, Roselle is grown extensively in Darfur and Kordofan states under rained conditions[15]. Roselle has antimicrobial antispasmodic and hypotensive effects as well as for uterine muscle relaxation[16]. The phytochemical content of Rosella that are reflected in the health of consumers enables its use in many functional food[17].

    Doum palm (Hyphaene thebaica) is a palm tree adapted to the desert and it has edible oval fruit with a potent antioxidants activity due to its high content of polyphenols[18]. The fruits of Doum palm (Hyphaene thebaica) are rich in dietary fibers and carbohydrates and it contains anti-hypertension substances[19]. Moreover, the edible portion of Doum fruits showed good values for dietary fiber and vitamins B1, B3, and B6, besides the total phenolic and flavonoid contents and its antioxidant activity that encourage its use in the formula of some functional foods[20]. Therefore, the objectives of the present study are the utilization of whey proteins produced by the dairy industry to develop whey-based beverages using some of the Sudanese indigenous fruits (Roselle, Baobab, and Doum palm) and test the quality of the obtained products. The gross chemical composition and the levels of vitamin C, calcium and phosphorus were compared within different whey proteins based beverages. Also the microbial content and some sensory attributes were compared for the different produced whey proteins beverages

    Materials and methods

    Source of liquid whey proteins

    The liquid whey remaining after the processing of Mozzarella cheese were obtained from the Dairy Production Department, Faculty of Animal Production, University of Khartoum, Sudan.

    Materials

    Roselle (Hibiscus sabdariffa L.) powder, Baobab (Adansonia digitata L.) powder, Doum palm (Hyphaene thebaica) powder, sugar and Gum Arabic were bought from the markets of Khartoum, Sudan.

    Methods

    Three liters of whey proteins were obtained after making Mozzarella cheese and sieved before being subjected to heating for 15 min at 75 °C. They were left to cool at a temperature of 10 °C. After that, they were filtrated using a clean cheesecloth and stored at room temperature.

    Preparation of indigenous fruit juices

    Sixty grams of Roselle (Hibiscus sabdariffa L.) powder was socked into 200 mL distilled water for 24 h and then filtrated. Meanwhile, 15 g of each Baobab (Adansonia digitata L.) and Doum (Hyphaene thebaica) powder were separately dissolved in 200 mL of clean distilled water. Then the three prepared juices were added to make different whey proteins beverages.

    Preparation of whey protein beverages

    During this experiment, 10 different whey proteins beverages were developed based on 3 different treatments in addition to the control (Plain whey proteins). The three treatment utilized 30:70%, 50:50%, and 70:30% of the heated liquid whey proteins that were added to the selected fruit juices. After making all the mixtures of the whey proteins and the fruits juices, about 15 g of sugar and 2.5 g of Gum Arabic were added to each of the prepared fruit juices and each was blended separately.

    Chemical analysis

    The chemical composition of whey protein beverages was performed according to the methods of the AOAC[21].

    The fat content was extracted by taking 10.94 mL of the whey proteins beverages sample and 10 mL sulfuric acid (density 1.815 gm/mL at 20 °C) into a clean dry Gerber. Then 1 mL of amyl alcohol (density 0.814–0.816 gm/mL at 20 °C) were added and the contents were thoroughly mixed till no white particles could be seen. After the centrifugation of the Gerber tubes (1,100 revolution per min) for 3 min, they were transferred into a water bath at 65 °C for 3 min and then the fat percent was taken directly from the fat column[21].

    The total protein content of the whey protein beverages was determined using the Kjeldahl method[21]. In a clean and dry Kjeldahl flask, 10 mL of the whey proteins beverages sample was placed followed by the addition of catalyst powder (Na2SO4 and the equivalent of 0.1 mg Hg). Then 25 mL concentrated sulfuric acid (density 1.86 gm/mL at 20 °C) was added to the flask and the mixture was then digested on a digestion heater until a clear solution was obtained (3 h). The flasks were then removed and left to cool and the digested samples were poured into volumetric flasks (100 mL) and diluted to 100 mL with distilled water. About 5 mL were taken and neutralized using 10 mL of 40% NaOH. The distillate was received into a conical flask containing 25 mL of 2% boric acid and 3 drops of 0.1 of bromocresol green and methyl red) indicator. This distillation was continued until the volume in the flask was 75 mL. The flasks were then removed from the distillates and titrated against HCl (0.1N) until the endpoint was obtained (red color). The protein content was calculated as follows:

    Nitrogen(%)=T×0.1×20×0.014Weightofsample×100
    Protein(%)=Nitrogen(%)×6.38

    Where, T: itration figure; 0.1: Normality of HCl; 0.014: Atomic weight of nitrogen; 20: Dilation factor.

    The content of lactose was determined using the anthrone method[22]. The reagent was added to the clear filtrate from precipitation of a sodium bicarbonate solution of the whey protein beverages with 0·1 n-sulphuric acid. The reagent consists of 0.15% (w/v) anthrone in 70% (v/v) sulphuric acid. Ten mL of the ice-cold anthrone solution was added, with cooling, to 1 mL of the ice-cold solution containing 0–100 µg of lactose. The mixture was heated at 100 °C for 6 min and then cooled for 30 min. The optical density of the colored solution was then measured at 625 nn using spectrophotometer (UV mini 1240), Shimadzo, Japan.

    The titratable acidity of whey proteins beverages was determined by taking 10 mL of the sample into a white porcelain dish and then 0.5 mL of phenolphthalein indicator was added. The titration was conducted using 0.1 N NaOH until a faint pink color that lasted for 30 s was obtained. The titration figures were then divided by 10 to get the percentage of the lactic acid[21].

    The ash content was determined according to the AOAC method[21] by weighing 5 mL of whey protein beverages sample into a suitable clean dry crucible and evaporating to dryness on a steam bath. The crucibles were placed in a muffle furnace at 550 °C for 1.5–2 h. It was cooled in a desiccator and weighted. The ash content was then calculated as follows:

    Ash(%)=W1W2×100

    Where, W1= Weight of ash; W2= Weight of sample.

    The solid's non-fat content where then calculated mathematically by adding the sum of lactose, protein, and ash content.

    Vitamin C content of the whey protein beverage samples (in duplicate) was determined by the method developed previously[23] using a UV/VIS Spectrophotometer (UNICAM, 8625).

    For the determination of calcium and phosphorus of whey proteins beverages samples, the residual of the ash extract was used. The phosphorus was determined by spectrophotometer (UV mini 1240), Shimadzo, Jaban. The estimation of phosphorous content was conducted using the vanadate-molybdate yellow calorimetric method[24]. Also the the calcium content was performed as was described previously[24]. The calcium content was determined by taking 5 mL of the ash extract solution into a 50 mL conical flask and the volume was completed to 25 mL by distilled water. Then 50 mg of meroxide indicator, 3−5 drops of sodium hydroxide were added, and the mixture was titrated against 0.01 N (EDTA). After calibration, the solution changed from pink to purple.

    Ca+Mgmmol/L=(V×N×1000)/5mL
    Cammol/L=(V×N×1000)/5mL

    Where, N: normality of EDTA; V: volume.

    Microbiological examination

    Plate count agar (Biomark, B 298) medium was used to determine the total bacterial count at 32 °C for 48 h. It was obtained in a dehydrated form and each rehydrated liter of the medium was composed of casein enzymic hydrolysate (5.0 g), yeast extract (2.5 g) dextrose (1.0 g), and agar (15.0 g). According to the manufacturers' instructions, 23.5 g were suspended in 1,000 mL distilled water; it was boiled until dissolved completely and sterilized

    The M17 broth media (HIMEDIA, M1029-500G) medium was obtained in dehydrated form and it was used for the enumeration of the lactic acid bacterial count after solidifying with the agar. This medium consists of casein enzymic hydrolysis 2.50 g/L, peptic digest of animal tissue 2.50 g/L, peptic digest of soyabean meal 5.00 g/L, yeast extract 2.50 g/L, beef extract 5.00 g/L, ascorbic acid 0.50 g/L, magnesium sulphate 0.25 g/L, lactose 5.00 g/L and disodium-B-glycerophosphate 19.00 mg/L. The final pH was adjusted to 7.1 ± 0.1 at 25 °C. About 42.25 g were suspended in 1,000 mL distilled water. The medium was dissolved completely and 13 g of the agar was added before the sterilization.

    The manufacturer' instructions were followed carefully for the preparation of both media, they were sterilized using the autoclave (15-pound pressure for 15 min)[25]. Similarly, the mixer, tips, and distilled water were sterilized using the autoclave (15 min at 121 °C)[25]. However, sterilization of glassware; Petri- dishes, test tubes, pipettes, flasks, and bottles; were done using dry heat (hot oven) at 160 °C for 1 h.

    The plate count agar medium was incubated at 32 °C for 48 h[26] and the lactic acid bacterial count was determined at 37 °C anaerobically for 24 h on M17 agar[27]. A colony counter was used to count the different types of colonies and the results were present as cfu/mL.

    Sensory evaluation

    The sensory evaluation was conducted according to a previously described method[28]. All the obtained data were evaluated using the penal test sheets.

    Statistical analysis

    The obtained data were subjected to Statistical Analysis Systems (SAS). A comparison of means was performed using Duncan Multiple Range test (p ≤ 0.05)[29]. A Microsoft Excel sheet was used to plot the figures.

    Results and dissection

    The chemical composition of whey proteins beverages

    The data obtained for the chemical composition of whey proteins beverages (Table 1) showed that the fat content in the different juices used was less than that obtained for the plain whey proteins. However, significantly (p ≤ 0.05) higher fat content was found in the whey enriched with Doum juice (0.93%) compared to other juices. This might be because the fruits of Doum palm have a slightly high content of fat (2.57%)[30]. Moreover, the functional properties of the essential nutrients that are possessed and provided by Doum fruits have an important role in addressing many problems related to food in patients with diabetic and hypertensive conditions[31]. The low values of the fat in the Baobab fruit pulp is the reason for the lowest mean obtained for fat content in whey proteins enriched with Baobab[13].

    Table 1.  Effect of fruits type on the chemical composition of whey proteins beverages.
    ParametersPlain whey proteinsWhey enriched with Baobab juiceWhey enriched with Roselle juiceWhey enriched with Doum juice
    Fat (%)1.03a0.71b0.36c0.93a
    Protein (%)4.45b1.41c5.79a5.33ab
    SNF (%)8.59c17.98a15.40b16.39ab
    Lactose (%)4.78d16.36a8.30c9.99b
    Acidity (%)0.48b0.38c0.30d0.58a
    Means with the same superscripts letters in the same column are not significantly different (p > 0.05).
     | Show Table
    DownLoad: CSV

    Significantly (p ≤ 0.05) higher protein content was obtained in whey proteins enriched with Roselle juice (5.79) followed by that enriched by Doum juice (5.33%) compared to the plain whey proteins (Table 1). Moreover, the proportion of protein content (6.46% and 6.29%) was found to increase with increasing of Doum juice (70% and 50%, respectively) as shown in Table 2 and this might be due to the protein content of Doum palm, which revealed 7.05%[30]. Also, the plain whey proteins revealed 4.45% proteins (Tables 1 & 2). Whey proteins contain highly nutritious food ingredients[3].

    Table 2.  Comparison of the chemical composition of whey proteins beverages using different type and concentration of fruits.
    ParametersConcentrations (%)Fat (%)Protein (%)SNF (%)Lactose (%)Acidity (%)
    Plain whey proteins−1.034.458.594.480.48
    Whey enriched with Baobab juice30:70−0.1718.4817.930.50
    50:502.130.3618.0017.160.37
    70:30−3.6917.1413.980.28
    Whey enriched with Roselle juice30:700.235.818.318.430.19
    50:500.175.8112.318.310.33
    70:300.145.7415.388.250.34
    Whey enriched with Doum juice30:700.266.4617.099.240.28
    50:500.256.2916.268.420.17
    70:300.083.2415.818.250.10
     | Show Table
    DownLoad: CSV

    The solid non-fat content of whey protein beverages revealed significantly (p ≤ 0.05) higher values for the whey protein beverages enriched with Baobab pulp (17.98%), followed by that enriched with Doum juice (16.39%) and Roselle juice (15.40%) compared to the plain whey proteins (8.59%). This could be because the Baobab fruit has a high content of carbohydrates (21.09%)[32]. Moreover, the carbohydrate content of dry Baobab fruit pulp is relatively high[33]. The reason could be because the total solids content of Baobab pulp are high[13].

    The significant (p ≤ 0.05) high lactose content (16.36%) was reported for the whey proteins enriched using Baobab juice (Table 1). This could be justified by the fact that the dry fruit pulp of Baobab is a rich source of carbohydrates[33].

    The titratable acidity in the whey enriched with Baobab revealed the highest significant (p ≤ 0.05) value (0.58%) followed by that obtained for the plain whey proteins (0.48%). The obtained higher value justified the use of Baobab in the fermentation of some foods. The obtained titratable acidity (0.38%−0.42%) in yogurt was found to comply with the required minimum standard (0.6%) stated for commercial yogurt[34].

    Table 3 showed significant (p ≤ 0.05) variations in the values of vitamin C in the different whey protein beverages. The significant (p ≤ 0.05) high content of vitamin C was found for Baobab enriched whey proteins (140.93 mg/100 mL). The obtained higher levels of vitamin C demonstrated the antioxidant properties of the three used fruit juices (Tables 3 & 4). Moreover, vitamin C content was found to increase with the increasing proportion of the Baobab juice extracts (167.22 and 166.39 mg/100 mL for 70% and 50%, respectively). The high vitamin C content of the raw Baobab fruit pulp justified these findings[10,11,33,34]. The value of vitamin C was found to increase with the increasing fortification level of Baobab pulp into yogurt[34]. Moreover, the high natural content of vitamin C in the pulp of Baobab fruit, enables its good antioxidant activity[35]. Vitamin C and A in Baobab fruit pulp were estimated as 236 and 80 mg/100 mL, respectively[36].

    Table 3.  Effect of fruit types on vitamin C and some minerals contents of whey proteins beverages.
    ParametersWhey enriched with Baobab juiceWhey enriched with Roselle juiceWhey enriched with Doum juice
    Vitamin C (mg/100 mL)140.93a91.28c129.28b
    Phosphorus (mg/100 mL)0.90b1.29a0.94b
    Calcium (mg/100 mL)1.23b8.50a0.93c
    Means bearing similar superscripts letters in the same column are not significantly different (p > 0.05).
     | Show Table
    DownLoad: CSV
    Table 4.  Effect of fruits type and concentration on the vitamin C and some minerals contents of whey proteins beverages.
    ParametersConcentrations
    (%)    		Vitamin C
    (mg/
    100 mL)    		Phosphorus
    (mg/
    100 mL)    		Calcium
    (mg/
    100 mL)
    Whey enriched with Baobab juice30:70167.220.870.70
    50:50166.390.591.40
    70:3089.190.551.60
    Whey enriched with Roselle juice 30:7056.241.232.30
    50:50101.231.852.30
    70:30116.252.110.90
    Whey enriched with Doum juice30:70156.170.731.30
    50:50139.440.980.80
    70:3092.221.130.70
     | Show Table
    DownLoad: CSV

    High level of vitamin C in Doum juice extract (129.28 mg/100 g) was also found during this study (Table 3). However, a lower value (31.74 mg/100 g) was reported for Doum fruit nectar samples[37]. This supported the fact that Doum fruit contains potent antioxidants[18]. Moreover, in a different product, it was reported that adding various percentages of powdered Doum fruit resulted in a proportional increase in the content of the total phenol as well as the antioxidant of the low-fat frozen yogurt compared with the control[38]. Also, the fermented milk of camel that was flavored using concentrated extracts of Doum was found to cause a significant increase in the content of phenolic components that showed correlation with the concentrations of the added levels of the juices[39]. On the other hand, the red pigment of Roselle showed a higher antioxidant activity when the fruit is consumed as beverages and the added Roselle extract resulted in more increase of the total phenolic content of yogurt fortified with different levels of Roselle extract and carrot juice[40].

    The calcium content that was obtained in the whey proteins enriched with the Roselle juice (8.50 mg/100 mL) revealed significantly (p ≤ 0.05) higher values (Tables 3 & 4). This might be because the Roselle extract is slightly higher in calcium content as was reported previously[41]. Similarly, high calcium content was obtained for the whey proteins enriched with the Baobab fruit juice extract supported the report, which stated that the fruit pulp of dry Baobab has a high content of calcium and vitamin C[33]. The Baobab fruit pulp contains about 295 mg/100 g of calcium[10]. The range of calcium in the Baobab was 4.10−4.30 mg/100 g[36]. The calcium requirements during growth, pregnancy, and lactation are increased[42]. Therefore, yogurt enriched the Baobab as a drink would be beneficial in maintaining the high calcium requirements for pregnant women, lactating mothers, children, and the elderly[34]. On the other hand, powdered Doum fruit contains adequate K, Ca, Na, and Mg[20,31,38]. Utilization of Doum palm (Hyphaene thebaica) powdered fruit showed useful application in food products because of its fiber and mineral content and its potential in health[43].

    The content of phosphorus reported for the whey proteins enriched with Roselle juice (1.29 mg/100 mL) showed significant (p ≤ 0.05) high values (Table 3). The phosphorus content was found to increase with increasing the used proportion of Roselle juice (Table 4). This reflected the richness of Roselle juice in its phosphorus content (2.78 mg/100 mL)[44]. However, the Baobab fruit content for phosphorus was in a range of 1.70−1.90 mg/100 g[36]. Among humans, a high content of phosphorus is desirable for increasing bone health[41].

    Microbiological findings of whey proteins beverages

    The microbial analysis of whey beverages (Table 5; Fig. 1) showed a high count for the total viable bacteria in the whey protein before heat treatment (log 5.10 vs 2.58), which matches very well with the objectives of heat treatment as a preservation method. The whey proteins enriched with Doum juice showed the lowest result for the total viable bacteria count (Table 5; Fig. 1). It was reported that Doum nectar did not show any viable bacteria during the storage period at the ambient and refrigeration temperatures[37]. Also, the antimicrobial activity of Hibiscus extracts against many bacteria was reported. Hence the extracts of H. sabdariffa have the potential to be used as antimicrobials in a food beverage system[14]. Information on microflora associated with the dried calyx of H. sabdariffa and its Zobo juice will help in designing appropriate techniques for the preservation of the juice[45]. The Hibiscus extracts have a potential use in the prevention of pathogenic growth in foods and beverages[14].

    Table 5.  Effect of fruits type and concentration on the microbiological loads of whey proteins beverages.
    ParametersConcentrations (%)Total violet bacterial countLactic acid bacterial count
    Whey proteins
    before heat
    treatment
    (Control A)    		5.103.72
    Whey proteins
    after heat
    treatment
    (Control B)    		2.582.49
    Whey enriched with Baobab juice30:703.692.99
    50:504.243.06
    70:303.263.00
    Whey enriched with Roselle juice30:703.283.17
    50:504.653.12
    70:303.273.07
    Whey enriched with Doum juice30:702.672,53
    50:503.093.48
    70:302.672.53
     | Show Table
    DownLoad: CSV
    Figure 1.  Variations of the microbiological loads of whey proteins beverages using different types and concentrations of fruits.
    DownLoad: Full-Size Img PowerPoint

    The total viable account was intermediate in whey proteins enriched with Baobab (Table 5; Fig. 1). Similarly, the 5% Baobab ice cream revealed a low total bacterial count compared to that made using 3% Baobab, which is indictive of its antimicrobial action[12]. This might be because its fruit pulp has higher values of vitamin C in addition to its antioxidant activity that play a positive role in reducing the microbial loads and hence extending the shelf-life of foods and beverages[32,35]. The microbial levels in formulated fruit juices should be 102 to 103 cfu/mL) according to the standards of the Sudanese Standards and Meteorology Organization[46].

    The lactic acid bacteria were higher in whey proteins enriched with Roselle fruit juice (Table 5; Fig. 1). This might be because the Roselle fruit juice extract is slightly higher in acidity content than other fruits used (Tables 1 & 2), which supported a previous findings[44]. Also, the present findings supported the previous report, which stated that the use of Doum palm extracts in the aqueous form will lead to the increase of both viability and activity of probiotics dairy starter cultures that are used in the manufacture of some special dairy products[47]. Moreover, the whey proteins drawn from cheese and buttermilk provide a suitable matrix for enhancing the growth and viability of probiotic microorganisms for the potential development of probiotic dairy-based beverages[48].

    In this study the base of the whey protein beverages is the Mozzarella cheese, hence some of the estimated useful lactic acid bacteria in the different whey proteins enriched juices are rich. This also supported the functional properties of the prepared juices as the health benefits of the starter cultures as a probiotic is well documented. The dairy-based whey proteins beverages display many health benefits because of their high contents of the antioxidant activity, bioactive peptides and the essential amino acids present in the whey[48,49]. In addition to their role in the mitigation of blood glucose and decreased appetite[50]. Thus, consuming dairy products enriched with probiotics provide anti-hyperglycemic effect and many other health benefits that depend upon the type of probiotic culture used and the consumed dairy products[51].

    Sensory attributes of whey protein beverages

    The sensory organoleptic evaluation of whey proteins beverages (Table 6; Fig. 2) showed that the whey proteins enriched with Roselle juice showed significantly (p ≤ 0.05) high acceptable score for color and this is because of its red color, which is due to the anthocyanins present in Roselle fruit[52]. When the extracts of Hibiscus are made into beverages or juice, its red color gained the desirability of the consumers[14]. The addition of Roselle extract (0.2%–0.4%) to carrot juice was found to improve the functional properties of yogurt and increased its sensory scores for up to 21 d[40]. Moreover, the US Food and Drug Administration has accepted H. sabdariffa as a natural flavoring substance because their calyces are extracted in water[14]. However, the whey enriched with Doum juice was significantly (p ≤ 0.05) high acceptable for its taste followed by Baobab. Similarly, higher scores were estimated for the sensory attributes with the addition of up to 33% powdered Doum fruit[38].

    Table 6.  Comparison of the sensory characteristics of whey proteins beverages using different types and concentrations of fruits.
    Fruit juiceConcentrations (%)ColorFlavorTaste
    Whey proteins enriched with Baobab juice30:701.702.602.30
    50:501.502.202.50
    70:302.502.601.60
    Whey proteins enriched with Roselle juice30:702.101.802.25
    50:501.802.452.45
    70:301.952.252.25
    Whey proteins enriched with Doum juice30:701.202.252.65
    50:501.452.253.00
    70:302.302.102.50
     | Show Table
    DownLoad: CSV
    Figure 2.  Variations of the sensory characteristics of whey proteins beverages using different fruits.
    DownLoad: Full-Size Img PowerPoint

    Significantly (p ≤ 0.05) higher scores were reported in the flavor of whey proteins enriched with Baobab (Table 6; Fig. 2). This is in line with the conclusion stating that adding 3% Baobab to camel milk ice cream resulted in an improvement of its flavor[12]. The significantly (p ≤ 0.05) high acceptability of Doum juice could be because using Doum palm fruit gave the product a sweet taste, special flavour, and colour[53]. Hence, there is a possibility of producing high quality fermented milk from camel with good appearance, colour, flavour, body and texture when adding Doum extract[39].

    Conclusions

    Variations reported for some of the compositional contents of the obtained whey protein beverages might be due to the different chemical composition of fruits used. The sensory evaluation showed the best result of the whey proteins enriched with the fruits of Doum palm (Hyphaene thebaica). The possibility of using some of the valuable Sudanese local fruits should be promoted and utilized for enriching the whey protein. This will help in improving the nutritional content and acceptability of the selected fruit juices and the whey proteins and thus contribute globally to obtain functional foods.

    Author contributions

    The contribution of the authors regarding this paper was as follows: study conception and design: Saied MNAM, El Zubeir IEM; collection of data: Saied MNAM; analysis and interpretation of the results: Saied MNAM; draft manuscript preparation: Saied MNAM, El Zubeir IEM. Both authors reviewed and approved the final version of the manuscript.

    Data availability

    The data generated and analyzed during the current study are available from the corresponding author (Ibtisam E. M. El Zubeir) on reasonable request.

    Acknowledgments

    The authors would like to extend their acknowledgments to the staff members in the Department of Dairy Production, Faculty of Animal Production, U. of K. for their technical help during the laboratory work.

  • The authors declare that they have no conflict of interest.

  • Supplemental Fig. S1 Photos of the seven genotypes that were treated for 8 weeks: control (left), EC5 (middle), and EC10 (right). The genotype arrangement in each treatment was randomized. Photos were taken right after trimming.
  • [1]

    Chavarria M, Wherley B, Thomas J, Chandra A, Raymer P. 2019. Salinity tolerance and recovery attributes of warm-season turfgrass cultivars. HortScience 54:1625−31

    doi: 10.21273/hortsci13963-19

    CrossRef   Google Scholar

    [2]

    Chaudhary J. 2019. Application of reclaimed water for irrigation: A review. (Accessed 9 Nov. 2022) https://soils.ifas.ufl.edu/media/soilsifasufledu/sws-main-site/pdf/technical-papers/Chaudhary_Juhi_Immediate_Release.pdf

    [3]

    United States Environmental Protection Agency (EPA). 2012. Guidelines for water reuse. EPA/600/R-12/618. (Accessed 10 Oct. 2022) https://www.epa.gov/sites/default/files/2019-08/documents/2012-guidelines-water-reuse.pdf
    [4]

    Chen W, Lu S, Jiao W, Wang M, Chang AC. 2013. Reclaimed water: A safe irrigation water source. Environmental Development 8:74−83

    doi: 10.1016/j.envdev.2013.04.003

    CrossRef   Google Scholar

    [5]

    Wu S, Sun Y, Niu G, Altland J, Cabrera R. 2016. Response of 10 aster species to saline water irrigation. HortScience 51:197−201

    doi: 10.21273/HORTSCI.51.2.197

    CrossRef   Google Scholar

    [6]

    Qian YL, Fu JM, Wilhelm SJ, Christensen D, Koski AJ. 2007. Relative salinity tolerance of turf-type saltgrass selections. HortScience 42:205−9

    doi: 10.21273/HORTSCI.42.2.205

    CrossRef   Google Scholar

    [7]

    Kronzucker HJ, Britto DT. 2011. Sodium transport in plants: a critical review. New Phytologist 189:54−81

    doi: 10.1111/j.1469-8137.2010.03540.x

    CrossRef   Google Scholar

    [8]

    Parida AK, Das AB. 2005. Salt tolerance and salinity effects on plants: a review. Ecotoxicology and Environmental Safety 60:324−49

    doi: 10.1016/j.ecoenv.2004.06.010

    CrossRef   Google Scholar

    [9]

    Flowers TJ, Munns R, Colmer TD. 2015. Sodium chloride toxicity and the cellular basis of salt tolerance in halophytes. Annals of Botany 115:419−31

    doi: 10.1093/aob/mcu217

    CrossRef   Google Scholar

    [10]

    Munns R, Tester M. 2008. Mechanisms of salinity tolerance. Annual Review of Plant Biology 59:651−81

    doi: 10.1146/annurev.arplant.59.032607.092911

    CrossRef   Google Scholar

    [11]

    Bernstein L, François LE, Clark RA. 1972. Salt tolerance of ornamental shrubs and ground covers. Journal of the American Society for Horticultural Science 97:550−56

    doi: 10.21273/JASHS.97.4.550

    CrossRef   Google Scholar

    [12]

    Niu G, Cabrera RI. 2010. Growth and physiological responses of landscape plants to saline water irrigation: A review. HortScience 45:1605−9

    doi: 10.21273/HORTSCI.45.11.1605

    CrossRef   Google Scholar

    [13]

    Marcum KB, Pessarakli M, Kopec DM. 2005. Relative salinity tolerance of 21 turf-type desert saltgrasses compared to bermudagrass. HortScience 40:827−29

    doi: 10.21273/HORTSCI.40.3.827

    CrossRef   Google Scholar

    [14]

    Wu Y, Chandra A, Genovesi AD, Meeks M. 2017. Freezing tolerance of field-and growth chamber-acclimated zoysiagrass hybrids. International Turfgrass Society Research Journal 13:421−26

    doi: 10.2134/itsrj2016.05.0427

    CrossRef   Google Scholar

    [15]

    Patton AJ, Schwartz BM, Kenworthy KE. 2017. Zoysiagrass (Zoysia spp.) history, utilization, and improvement in the United States: A review. Crop Science 57:S37−S72

    doi: 10.2135/cropsci2017.02.0074

    CrossRef   Google Scholar

    [16]

    Meeks M, Kong ST, Genovesi AD, Smith B, Chandra A. 2022. Low-input golf course putting green performance of fine-textured inter- and intra-specific zoysiagrass (Zoysia spp.). International Turfgrass Society Research Journal 14:610−21

    doi: 10.1002/its2.63

    CrossRef   Google Scholar

    [17]

    Marcum KB, Anderson SJ, Engelke MC. 1998. Salt gland ion secretion: A salinity tolerance mechanism among five zoysiagrass species. Crop Science 38:806−10

    doi: 10.2135/cropsci1998.0011183X003800030031x

    CrossRef   Google Scholar

    [18]

    Maeda Y. 2019. Effects of calcium application on the salt tolerance and sodium excretion from salt glands in zoysiagrass (Zoysia japonica). Grassland Science 65:189−96

    doi: 10.1111/grs.12234

    CrossRef   Google Scholar

    [19]

    Marcum KB, Murdoch CL. 1994. Salinity tolerance mechanisms of six C4 turfgrasses. Journal of the American Society for Horticultural Science 119:779−84

    doi: 10.21273/JASHS.119.4.779

    CrossRef   Google Scholar

    [20]

    Qian YL, Engelke MC, Foster MJV. 2000. Salinity effects on zoysiagrass cultivars and experimental lines. Crop Science 40:488−92

    doi: 10.2135/cropsci2000.402488x

    CrossRef   Google Scholar

    [21]

    Cavins TJ, Whipker BE, Fonteno WC. 2008. PourThru: A method for monitoring nutrition in the greenhouse. Acta Horticulturae 779:289−98

    doi: 10.17660/actahortic.2008.779.35

    CrossRef   Google Scholar

    [22]

    Havlin JL, Soltanpour PN. 1980. A nitric acid plant tissue digest method for use with inductively coupled plasma spectrometry. Communications in Soil Science and Plant Analysis 11:969−980

    doi: 10.1080/00103628009367096

    CrossRef   Google Scholar

    [23]

    Isaac RA, Johnson WC. 1975. Collaborative study of wet and dry ashing techniques for the elemental analysis of plant tissue by atomic absorption spectrophotometry. Journal of Association of Official Analytical Chemists 58:436−40

    Google Scholar

    [24]

    Gavlak RG, Horneck DA, Miller RO. 1994. Plant, Soil, and Water Reference Methods for the Western Region. Corvallis, OR, USA: Western Regional Extension Publication.
    [25]

    Grismer ME. 1990. Leaching fraction, soil salinity, and drainage efficiency. California Agriculture 44:24−26

    doi: 10.3733/ca.v044n06p24

    CrossRef   Google Scholar

    [26]

    Franco JA, Martínez-Sánchez, JJ, Fernández JA, Bañón S. 2006. Selection and nursery production of ornamental plants for landscaping and xerogardening in semi-arid environments. The Journal of Horticultural Science and Biotechnology 81:3−17

    doi: 10.1080/14620316.2006.11512022

    CrossRef   Google Scholar

    [27]

    Sainju UM, Allen BL, Lenssen AW, Ghimire RP. 2017. Root biomass, root/shoot ratio, and soil water content under perennial grasses with different nitrogen rates. Field Crops Research 210:183−191

    doi: 10.1016/j.fcr.2017.05.029

    CrossRef   Google Scholar

    [28]

    Beard JB, Green RL. 1994. The role of turfgrasses in environmental protection and their benefits to humans. Journal of Environmental Quality 23:452−60

    doi: 10.2134/jeq1994.00472425002300030007x

    CrossRef   Google Scholar

    [29]

    Marcum KB, Pessarakli M. 2006. Salinity tolerance and salt gland excretion efficiency of bermudagrass turf cultivars. Crop Science 46:2571−74

    doi: 10.2135/cropsci2006.01.0027

    CrossRef   Google Scholar

    [30]

    Fu JM, Koski AJ, Qian YL. 2005. Responses of creeping Bentgrass to salinity and mowing management: growth and turf quality. HortScience 40:463−67

    doi: 10.21273/HORTSCI.40.2.463

    CrossRef   Google Scholar

  • Cite this article

    Hooks T, Masabni J, Ganjegunte G, Sun L, Chandra A, et al. 2022. Salt tolerance of seven genotypes of zoysiagrass (Zoysia spp.). Technology in Horticulture 2:8 doi: 10.48130/TIH-2022-0008
    Hooks T, Masabni J, Ganjegunte G, Sun L, Chandra A, et al. 2022. Salt tolerance of seven genotypes of zoysiagrass (Zoysia spp.). Technology in Horticulture 2:8 doi: 10.48130/TIH-2022-0008
    shu

Figures(4)  /  Tables(3)

Download PDF

Article Metrics

Article views(5001) PDF downloads(752)

Other Articles By Authors

ARTICLE   Open Access    

Salt tolerance of seven genotypes of zoysiagrass (Zoysia spp.)

  • 1.

    Texas A&M AgriLife Research and Extension Center, 17360 Coit Rd, Dallas, TX 75252, USA

  • 2.

    Biosystems Engineering Department, University of Arizona, 1951 E. Roger Road, Tucson, AZ 85719, USA

  • 3.

    Texas A&M AgriLife Research, 1380 A&M Circle, El Paso, TX 79927, USA

  • 4.

    Department of Agriculture, Collin College, 391 Country Club Road, Wylie, TX 75098, USA

  • Received: 06 October 2022
  • Accepted: 24 November 2022
  • Published online: 13 December 2022
Technology in Horticulture  2,  Article number: 8  (2022)  |  Cite this article

Abstract: Seven zoysiagrass genotypes were evaluated for salt tolerance in a greenhouse study. The plant materials included Zoysia matrella 'Diamond', Z. japonica 'Palisades', three Z. matrella × Z. japonica hybrids DALZ 1701, DALZ 1713, and 'Innovation', and two Z. minima × Z. matrella hybrids (DALZ 1309 and 'Lazer'). Treatments included a control (nutrient solution) and two saline treatments representing moderate and high salt levels. The electrical conductivity (EC) was 1.3 dS m−1 for control and moderate (EC5) and high salinity (EC10) were 5.0 and 10.0 dS m−1, respectively. At the end of eight-weeks of treatment, the relative (percent control) shoot dry weight (DW) was greatest in 'Diamond' in EC10, and the relative root DW was greatest in DALZ 1309 in EC5. A cluster analysis based on the relative tissue dry weight identified 'Diamond', DALZ 1309, and DALZ 1713 as the most salt tolerant genotypes. Additionally, the green leaf area (GLA) index of 'Diamond' and DALZ 1713 were 98.8% and 100%, respectively, indicating excellent visual appearance under high salt levels. Bi-weekly clipping DW showed that 'Diamond' continued to produce biomass throughout the duration of the study under the EC10 treatment. Sodium (Na+) and chloride (Cl−) content in the shoot tissue of the seven turfgrass genotypes indicated that lower concentrations corresponded to greater salt tolerance indicating exclusion of Na+ and Cl− from the shoot tissue. Taken together, the genotypes 'Diamond' and DALZ 1713 were determined to be the most salt tolerant and recommended for use in areas with high soil or water salinity.

    HTML

    INTRODUCTION

    • Turfgrass is an important landscape groundcover that is widely used, not only for its aesthetics, but also for its function, such as in lawns, parks, athletic fields, and golf courses. However, in arid and semi-arid regions of the United States where fresh water sources are limited, reclaimed water sources that typically have elevated salt levels are increasingly being used for landscape irrigation[1,2]. Reclaimed water, also known as recycled or reused water, is non-potable wastewater from a variety of sources, including residential, industrial, or stormwater runoff[2]. Reclaimed water can be treated to varying degrees to be suitable for a wide range of uses, including agricultural and landscape irrigation, that effectually relieves the demand from freshwater sources[3]. Because of these benefits, reclaimed water is increasingly being used for irrigation in arid and semi-arid regions, particularly for turfgrass areas[4]. However, reclaimed water sources are typically saline, with high concentrations of sodium and chloride, which can be detrimental to the growth and aesthetic quality of salt-sensitive plants[5]. Therefore, there is a continued need for salt tolerant turfgrasses for sustainable landscaping in arid or semi-arid regions in order to utilize saline, reclaimed water sources and conserve fresh water sources, especially in the Southwestern U.S.[6].

      Sodium and chloride are the two major soluble salts that can be detrimental to glycophytes at high concentrations[7]. When these salts accumulate in the rhizosphere, they can impose osmotic stress on the plant, which leads to the inhibition of water uptake and can rapidly reduce plant growth and even lead to mortality[8]. If salts are taken up by the roots and translocated to the shoots, then ionic stress can occur which can result in metabolic disruption in the cytosol of cells, as well as damage to chloroplasts by reactive oxygen species (ROS)[9]. Ionic stress can lead to leaf burn, which appears as brown and necrotic tissue[10] and can significantly degrade the quality of landscape and ornamental plants[11]. For turfgrasses, it is important that salt tolerant cultivars are not susceptible to ionic stress and leaf burn and can maintain an appearance that is aesthetically appealing under saline conditions[12].

      Traditionally, bermudagrasses (Cynodon spp.) have been used as warm season turfgrasses for landscaping in arid and semi-arid regions, although they are considered high water consumption plants[13]. Alternatively, zoysiagrasses (Zoysia spp.) are warm season turfgrasses that are moderately tolerant to salinity and have good potential for the selection and development of new salt tolerant cultivars that can be irrigated with saline, reclaimed water sources[14,15]. Both bermudagrasses and zoysiagrasses are being used as breeding material for new cultivars with the aim of having warm season, salt tolerant varieties that can grow well and maintain high visual quality, or greenness, when irrigated with saline water.

      Zoysiagrass was originally introduced to the U.S. in 1892, from East Asia, and have since been very influential in the turfgrass industry with more than 50 cultivars that have been developed, particularly for stress and pest tolerances. Two major species, Z. japonica and Z. matrella, readily hybridize with each other and are known for high quality turfgrasses primarily used in residential and commercial lawns, and golf courses[15]. Another species, Z. minima, is native to New Zealand and has a diminutive growth habit that has potential for use in golf course putting greens[16]. The recognized salt tolerance of zoysiagrasses is largely based on their ability to excrete salt out of their leaves through specialized salt glands[17,18]. However, differences in salt tolerance have been noted among species and cultivars. Marcuum & Murdoch[19] reported greater salt tolerance in Z. matrella compared to Z. japonica under solution culture up to 400 mM (approximately 30 dS m−1) NaCl. Qian et al.[20] reported differences in relative salt tolerance among 29 zoysiagrass experimental lines and cultivars under solution culture up to 42.5 dS m−1.

      In the present study, seven genotypes of zoysiagrass (Zoysia spp.), including several hybrids, were selected for evaluation for salt tolerance in a greenhouse study. The seven genotypes were developed by the turfgrass breeding program at Texas A&M AgriLife (Texas, USA). The parent species for these seven genotypes represent different leaf morphologies and traits: Z. japonica, wide leaf blade with drought and cold tolerance; Z. matrella, fine leaf blade with salt and shade tolerance; and Z. minima, very fine leaf blade with shade tolerance and good visual quality. The objectives of the study were to identify salt tolerant genotypes for the continued improvement of salt tolerance in turfgrass breeding programs, and for the potential use of these genotypes for landscaping under saline conditions in arid and semi-arid regions of the US.

    MATERIALS AND METHODS

      Plant material and culture

    • Seven turfgrass genotypes were acquired from the Texas A&M AgriLife Turfgrass Breeding Program and used in this study, including a Z. matrella cultivar 'Diamond', a Z. japonica 'Palisades', three Z. matrella × Z. japonica hybrids DALZ 1701 ([(Z. matrella × Z. matrella) × Z. japonica] × Z. japonica), DALZ 1713 ([Z. japonica × (Z. matrella × Z. matrella)], and 'Innovation' (Z. matrella × Z. japonica), and two Z. minima × Z. matrella hybrids (DALZ 1309 and 'Lazer'). Approximately 10 rhizomes were transplanted into 10-cm (top diameter) round plastic pots (volume: 450 mL, height: 8.5 cm) filled with potting mix (Sun Gro, Agawam, MA, USA) and fertigated through the surface of the pot with 20-10-20 (N-P2O5-K2O) Peters Excel fertilizer (ICL, Sommerville, SC, USA) at a rate of 150 mg L−1 N, on an as-needed basis (when the substrate surface became dry). The nutrient solution was made by mixing 1.0 g of the above fertilizer to 1 L of tap water. The final electrical conductivity (EC) and pH was 1.3 dS m−1 and 6.5, respectively. Turfgrass cuttings were established and rooted for four weeks in a greenhouse at the Texas A&M AgriLife Research Center in Dallas, Texas (USA). A total of 24 pots with uniform growth of each genotype were selected. The genotypes were randomized on a greenhouse bench for the initiation of the saline treatments.

      Saline treatments

    • Two saline treatments were used, in addition to a non-saline control, in this experiment. In the control group, plants were irrigated with the nutrient solution as mentioned above. The two saline treatments were prepared by the addition of NaCl to the nutrient solution to achieve EC levels of 5.0 dS m−1 (EC5) and 10.0 dS m−1 (EC10). These two salinity levels were chosen based on available information in the literature on salt tolerance of other turfgrasses. The treatment solution for EC5 or EC10 was prepared by adding 230 g or 550 g of NaCl to 100 L nutrient solution. The actual EC and pH were recorded each time. Treatments were applied to the plants overhead on an as-needed basis. Approximately 200 mL was applied to each plant/pot per treatment application which provided a leaching fraction of approximately 35% to reduce the accumulation of salts in the substrate throughout the experiment. The experiment was arranged in a split-plot design with treatments randomized in greenhouse benches and genotypes randomized within treatments. There were eight pots (replicates) per treatment. Weekly measurements of the leachate EC and pH were recorded to track the salinity level in the substrate and rhizosphere. The leachate was collected via the 'Pourthru' method as described by Cavins et al.[21]. The treatments were initiated on 06 May 2020 and lasted eight weeks and was terminated on 02 July 2020.

      Greenhouse environment

    • The experiment was conducted in a greenhouse at the Texas A&M AgriLife Research Center in Dallas, TX, USA (32°59'13.2" N 96°45'59.8" W; elevation 131 m). The greenhouse air temperature was controlled by an evaporative cooling wall and two exhaust fans. A 50% shade fabric was used throughout the experiment to reduce sunlight and heat in the greenhouse. Throughout the experiment, greenhouse air temperature and photosynthetic active radiation (PAR) were recorded by a datalogger (Campbell Scientific, Logan, UT, USA). The air temperature and quantum sensor (for PAR measurement) were installed right above the bench to capture the actual air temperature and light intensity near the plant canopy. The daily average air temperature during the experiment was 26.0 ± 3.56 °C (mean ± standard deviation) and the average daily light integral (DLI) was 12.0 ± 2.98 mol m−2 d−1.

      Data collection

    • Throughout the experiment, the plants were clipped on a biweekly schedule and the clippings were collected and dried in a drying oven at 70 °C for dry weight determination. Clipping was accomplished by hand with scissors and a ruler, following a treatment application. The turfgrass was clipped to a 2-cm height and the perimeter of the pots were also trimmed. Additionally, after each biweekly trimming, the percent canopy green leaf area (GLA) was determined visually by two persons to assess the quality of the plants under the saline treatments. At harvest, shoot and root tissue were separated and dried in a drying oven at 70 °C for biomass determination. Roots were washed of substrate and rinsed briefly in reverse osmosis water before being placed in paper bags and dried in the drying oven. Following dry weight determination, three shoot samples from each treatment were ground in a Wiley mill (Thomas Scientific, Swedesboro, NH, USA) to pass a 40-mesh screen. Shoot tissue mineral contents were analyzed using inductively coupled plasma mass spectrometry (ICP-MS) using the methods described by Havlin & Soltanpour[22] and Isaac & Johnson[23]. Shoot tissue chloride content was determined by extraction with 2% acetic acid and analyzed using an M926 Chloride Analyzer (Cole Parmer Instrument Company, Vernon Hills, IL, USA) according to the methods described by Gavlak et al.[24]

      Statistical analysis

    • There was a total of three treatments and seven genotypes with eight replications each (N = 168). Data were analyzed as a two-way analysis of variance (ANOVA) with an alpha of 0.05 using JMP 15 (SAS, Cary, NC, USA). Means were separated using Tukey's Honest Significant Difference (HSD) test with an alpha of 0.05. Relative shoot dry weight (DW) was calculated as the shoot DW in the saline treatment/average shoot DW in control × 100%. Relative root DW and relative total DW in percentage were calculated in a similar fashion compared to control. Student's t-test was used for comparing the relative growth parameters between the two saline treatments.

    RESULTS

      Leachate Electrical conductivity (EC)

    • Throughout the duration of the study, leachate EC of the control, moderate, and high salt treatments averaged 1.7, 7.4, and 14.2 mS cm−1, respectively (Fig. 1). Although leachate EC increased steadily in the moderate and high salt treatments throughout most of the study due to a buildup of salts in the substrate, the averages of the treatments were significantly different, as expected. The maximum EC of the salt treatments peaked during week six, at 11.2 and 18.8 dS m−1 for the moderate and high salt treatments, respectively. During weeks seven and eight, the EC of the salt treatments started to decline which was attributed to the retention of moisture in the substrate due to reduced water uptake by the osmotically stressed grasses, which ultimately lead to increased leaching fractions during irrigation.

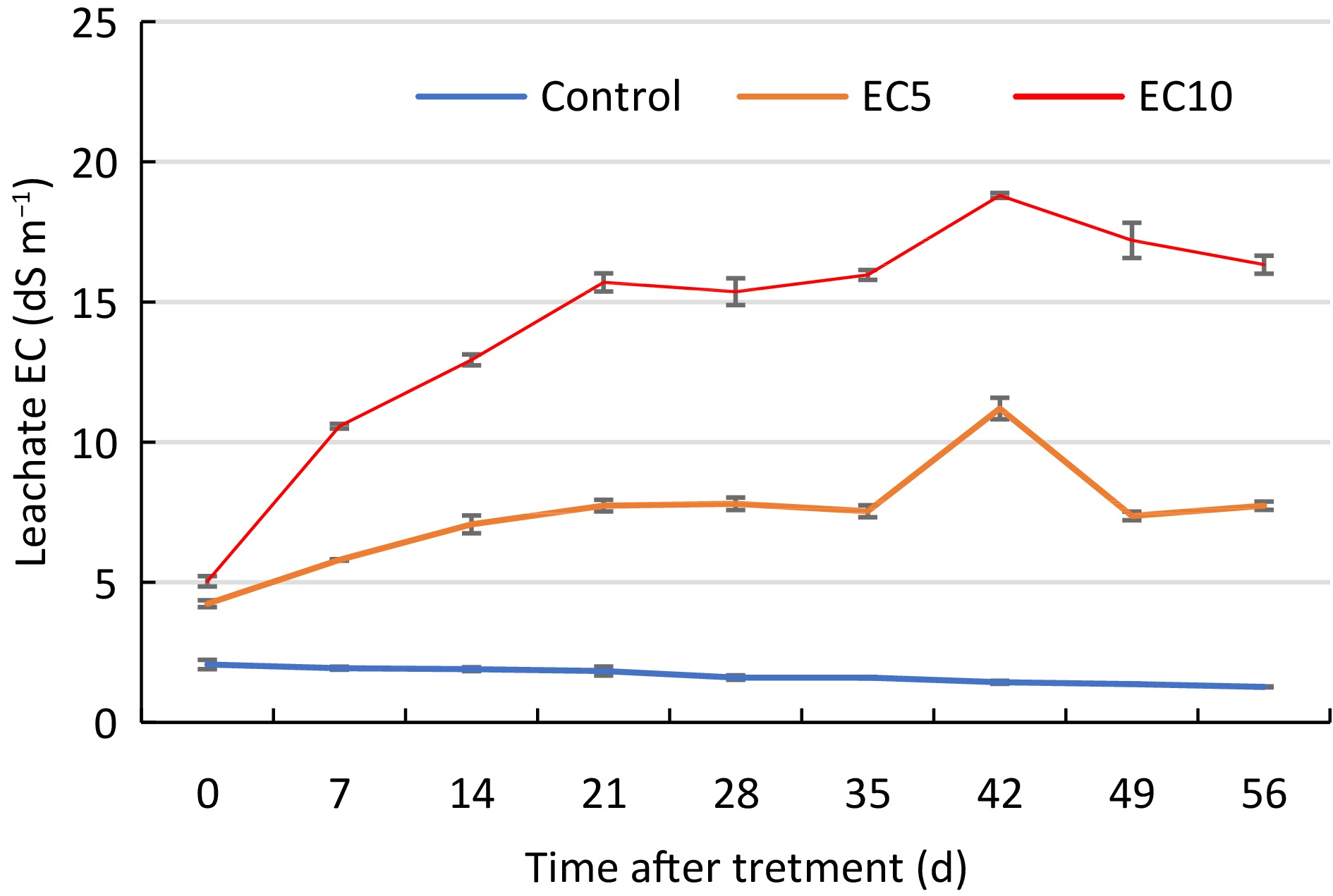
      Figure 1. 

      Electrical conductivity (EC) of leachate collected from seven turfgrass genotypes treated with control or saline solutions (EC5 or EC10) for a total of eight weeks. Vertical bars indicate standard error (n = 5).

      Relative tissue dry weight (DW)

    • For relative (percent control) shoot DW, there were no treatment differences but there were significant genotype differences in the EC10 treatment (Table 1), as expected, with Diamond showing the greatest increase of 130% compared to the control (Fig. 2). For relative root DW, there were significant treatment differences in Lazer and DALZ 1713, with reductions of 20% and 40%, respectively, in the EC10 treatment. There were genotypic differences in the EC5 treatment only, with DALZ 1309 showing the greatest increase of 130% compared to the control, while DALZ 1701 and Palisades decreased by 15% and 17%, respectively, compared to the control. Overall, for total DW, there were significant treatment differences in Lazer and DALZ 1713, with reductions of 20% and 22%, respectively, in the EC10 treatment. Both salt treatments had significant genotype differences, with DALZ 1309, DALZ 1713, and Diamond showing the greatest increases of 120%, 122%, 118%, respectively, in the EC5 treatment compared to the control, while Diamond showed the greatest increase of 121% in the EC10 treatment.

      Table 1.  ANOVA summary of the response variables of the seven zoysiagrass genotypes irrigated with a nutrient solution (control) or saline solution at electrical conductivity (EC) of 5 dS m−1 or 10 dS m−1 for eight weeks. The response variables are shoot DW (dry weight), root DW, total DW, relative shoot DW (R. shoot DW), relative root DW (R. root DW), relative total DW (R. total DW), green leaf area (GLA), cumulative clipping DW, shoot sodium (Na) and chloride (Cl) concentration.

      SourceShoot DWRoot DWTotal DWR. Shoot DWR. Root DWR. Total DWGLAClipping DWShoot Na+Shoot Cl−
      Model0.0004< 0.0001< 0.00010.00030.0001<.0001< 0.0001< 0.0001< 0.0001< 0.0001
      Treatment (T)0.0080.00010.001NS0.00020.0013< 0.0001< 0.0001< 0.0001< 0.0001
      Genotype (G)0.0006< 0.0001< 0.0001< 0.00010.0014< 0.0001< 0.0001< 0.0001< 0.0001< 0.0001
      T × GNS0.04240.0109NSNSNS< 0.0001< 0.0001< 0.0001< 0.0001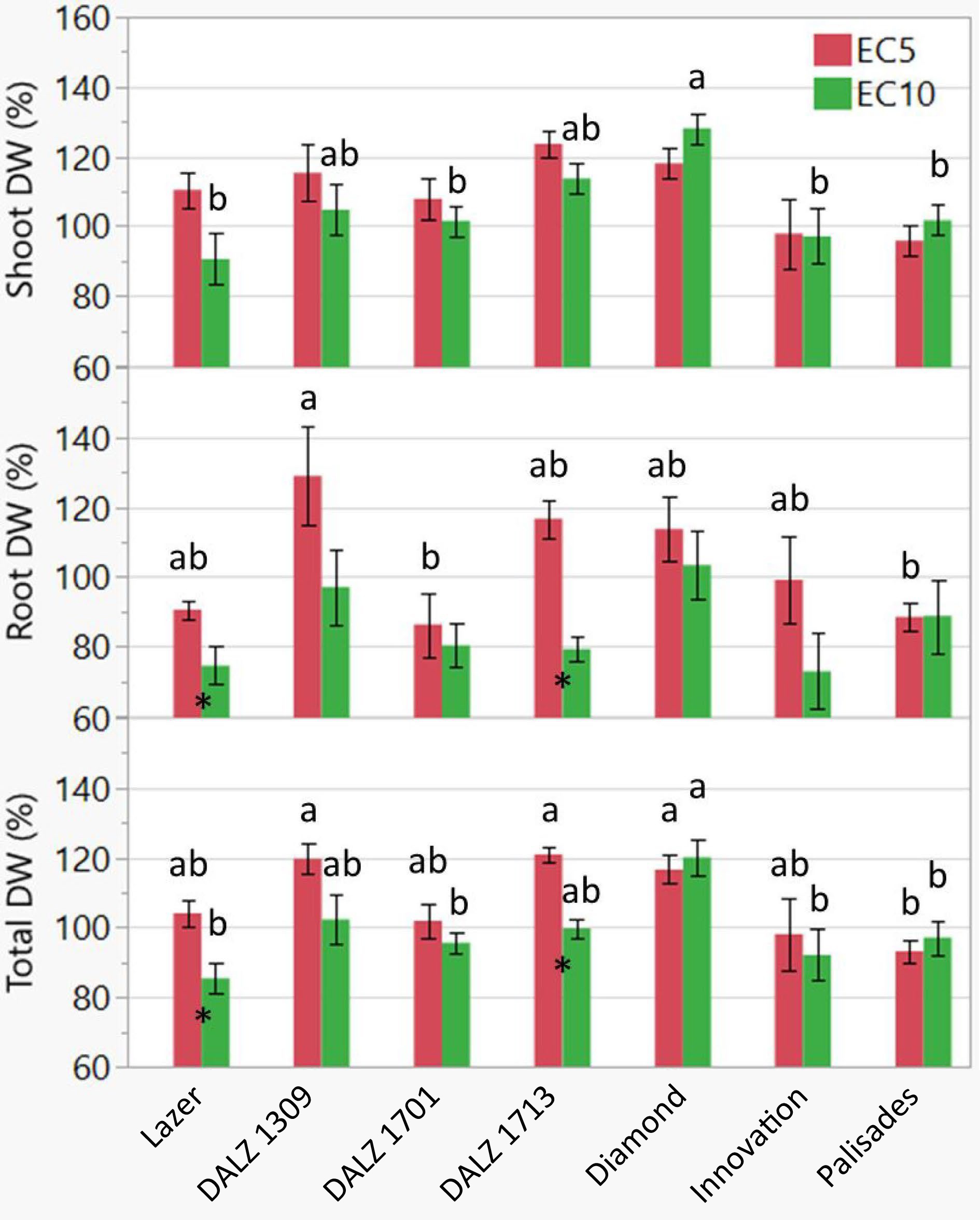

      Figure 2. 

      Relative (percent of control) dry weight (DW) of shoot and root tissue, and the total (shoot + root) of the seven turfgrass genotypes treated with control or saline solutions (EC5 or EC10) for a total of eight weeks. Bars represent standard error (n = 8). Different letters indicate significant differences among genotypes for the same treatment according to Tukey's HSD test (P < 0.05). That is, the comparison was made for EC5 (red bars) or EC10 (green bars) separately. For those without any letters such as EC5 for shoot DW, no difference was observed. Asterisks indicate significant differences between treatments (EC5 and EC10) according to Student's t-test (P < 0.05). No asterisks mean no differences.

      Hierarchal cluster analysis

    • A cluster analysis was performed on the relative shoot and root DW of the seven turfgrass genotypes treated with moderate and high salinity and found two distinct clusters as indicated by the distance graph (Fig. 3). Cluster 1 (red) indicates the least salt tolerant genotypes (based on lowest relative tissue DW) and included Lazer, DALZ 1701, Innovation, and Palisades. Cluster 2 (green) indicates the most salt tolerant genotypes (based on greatest relative tissue DW) and included DALZ 1309, DALZ 1713, and Diamond.

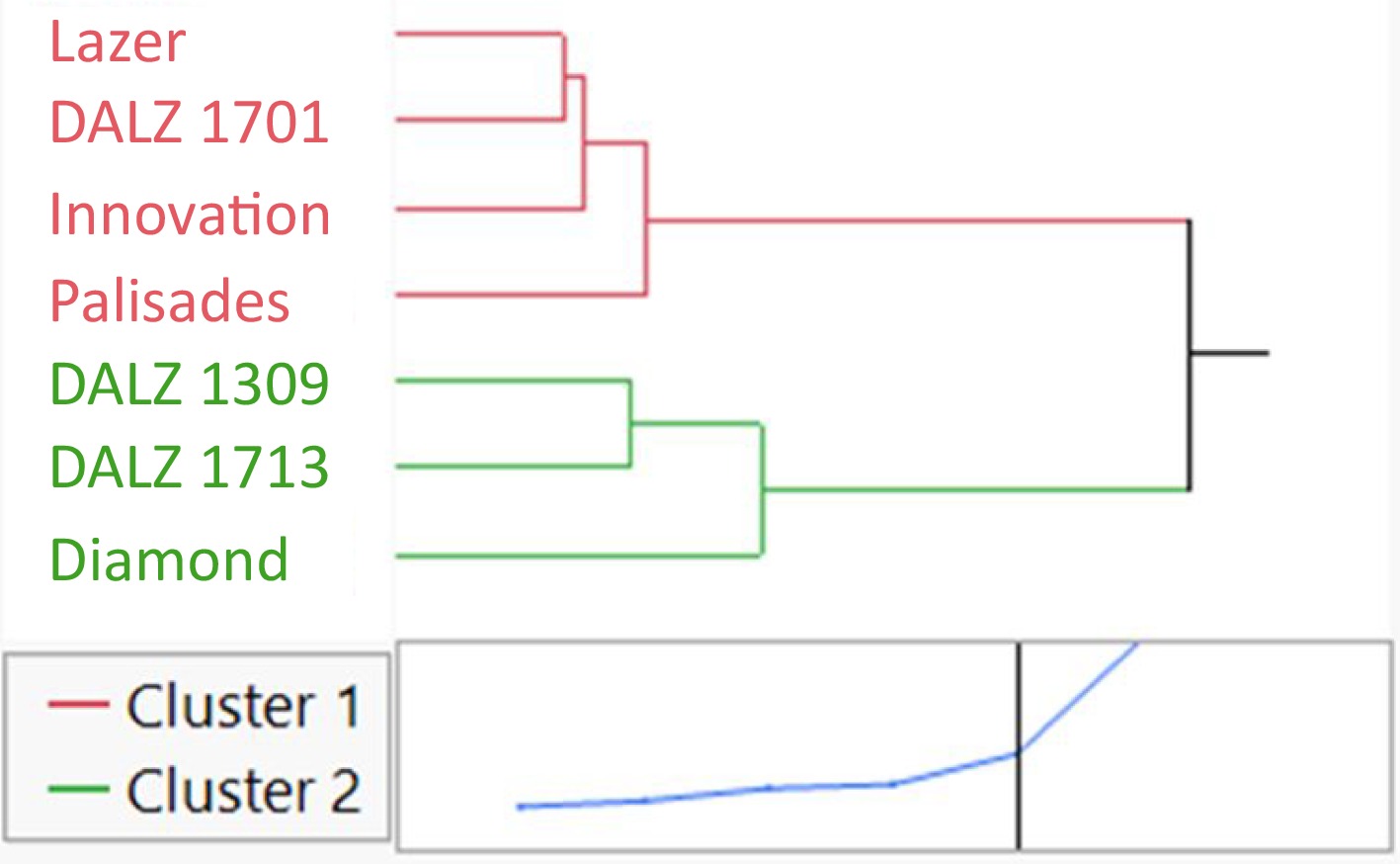
      Figure 3. 

      Hierarchal cluster analysis based on relative (percent of control) tissue dry weight (DW) of the seven turfgrass genotypes treated with control or saline solutions (EC5 or EC10) for a total of eight weeks. Cluster 1 (red) indicates the least salt tolerant genotypes and Cluster 2 (green) indicates the most salt tolerant genotypes. The two clusters were determined by the distance graph at the bottom of the figure that shows the best separation between clusters.

      Green Leaf Area (GLA) index

    • The GLA Index averaged 98.7 in the control, 96.7 in the EC5 treatment, and 92.4 in the EC10 treatment (Table 2, Supplemental Fig. S1). There were significant treatment, genotype, and treatment × genotype interactions in GLA (Table 1). The interactions were attributed to DALZ 1309 showing substantial reductions in GLA in the EC10 treatment, while other genotypes such as DALZ 1713, showing no reductions. In fact, DALZ 1309 showed the greatest reductions in GLA in all treatments, specifically 95.6, 88.8, and 69.4 in the control, EC5, and EC10 treatments, respectively. In contrast, DALZ 1701, DALZ 1713, Diamond, and Palisades showed no significant differences in GLA among the treatments and maintained excellent scores under the saline irrigation treatments.

      Table 2.  Green Leaf Area (GLA) index of the seven turfgrass genotypes treated with control or saline solutions (EC5 or EC10: electrical conductivity at 5 or 10 dS m−1) for a total of eight weeks. Means and standard errors are presented (n = 8). The GLA was assessed visually following a clipping.

      GenotypeControlEC5EC10
      Lazer100.0 ± 0.0Aa99.4 ± 0.6Aab95 ± 2.1Ab
      DALZ 130995.6 ± 2.0Ba88.8 ± 3.0Ca69.4 ± 6.4Bb
      DALZ 170198.1 ± 0.9ABa99.4 ± 0.6Aa97.5 ± 0.9Aa
      DALZ 1713100.0 ± 0.0Aa99.4 ± 0.6Aa100.0 ± 0.0Aa
      Diamond99.4 ± 0.6ABa100.0 ± 0.0Aa98.8 ± 1.3Aa
      Innovation98.1 ± 1.3ABa91.9 ± 2.5BCab88.1 ± 3.3Ab
      Palisades100.0 ± 0.0Aa98.1 ± 0.9ABa98.1 ± 0.9Aa
      Different letters indicate significant differences Tukey's HSD test; uppercase among genotypes and lowercase among treatments.

      Clipping Dry Weight (DW)

    • For Clipping DW, there were significant treatment, genotype, and treatment × genotype interactions (Table 1). The interactions can be explained by some genotypes showing an increase in clipping DW in all treatments throughout the study, while other genotypes showed a decrease, particularly in the EC10 treatment during the final weeks of the study (Fig. 4). There were significant treatment differences as early as week 2 in DALZ 1701 and Palisades, and in all genotypes for the remaining weeks of the study. Overall, clipping DW was greatest in the control, followed by the EC5 and then EC10 treatment. By the end of the study, clipping DW in EC5 and EC10 plateaued or declined in all genotypes except for Lazer, DALZ 1309, DALZ 1701 (EC5), and Diamond (EC10), which still showed increases despite the high saline conditions as indicated by the leachate EC. Declines in the control treatment towards the end of the study in DALZ 1713, Innovation, and Palisades can be attributed to the plants exceeding the growth capacity of the containers.

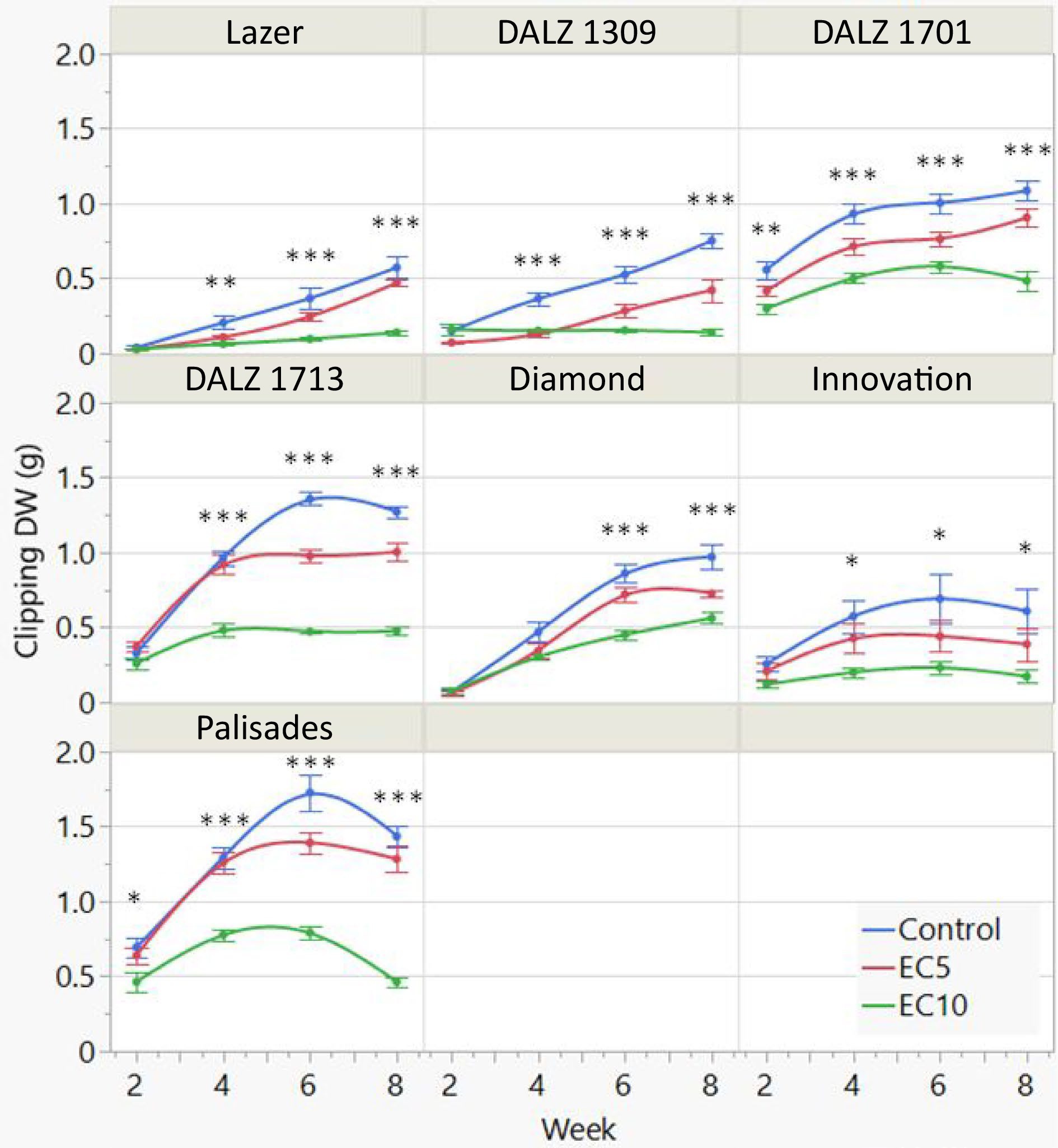
      Figure 4. 

      Bi-weekly clipping dry weight (DW) of the seven turfgrass genotypes treated with control or saline solutions (EC5 or EC10: electrical conductivity at 5 or 10 dS m−1) for a total of eight weeks. The plants were clipped to a height of 2-cm. Bars represent standard error (n = 8). Significant differences among treatments per week are indicated by asterisks (*, P < 0.05; **, P < 0.01; and ***, P < 0.001).

      Tissue sodium and chloride content

    • There were significant treatment, genotype, and treatment x genotype interactions for both sodium (Na+) and chloride (Cl−) concentrations in the shoot tissue (Table 1). Overall, the Na+ and Cl− concentrations in the shoot tissue increased in the salt treatments compared to the control, as expected due to the higher amount of Na+ and Cl− ions in the salt treatments (Table 3). The average Na+ concentration in the tissue of plants treated with control, EC5, and EC10 was 2.00, 8.49, and 12.04 mg g−1, respectively. For Cl−, the average amount was 6.41, 12.53, and 18.54 mg g−1 in the tissue of plants treated with control, EC5, and EC10, respectively. For Na+ there were no significant differences among genotypes in the EC5 treatment, although in the EC10 treatment genotype DALZ 1309 had the greatest concentration (15.68 mg g−1) while DALZ 1701 had the least (7.92 mg g−1). For Cl− in the EC5 treatment, the genotype Palisades had the greatest concentration (15.97 mg g−1) while Lazer and DALZ 1701 had the least (9.72 and 9.68 mg g−1, respectively). In the EC10 treatment, the genotypes DALZ 1309 and Innovation had the greatest concentrations (23.97 and 25.18 mg g−1), while Lazer, DALZ 1701, and Diamond, had the least (14.00, 13.25, 15.38 mg g−1, respectively). Regarding the significant interaction, this can be explained by most genotypes showing substantial increases of Na+ and Cl− between the EC5 and EC10 treatments, while certain genotypes showed no differences, such as Lazer in the EC5 treatment and Palisades in the EC10 treatment.

      Table 3.  Sodium (Na+) and chloride (Cl−) content in the tissue of the seven turfgrass genotypes that were treated with control or saline solutions (EC5 or EC10: electrical conductivity at 5 or 10 dS m−1) for a total of eight weeks.

      GenotypeControlEC5EC10
      Na+
      Lazer1.70 ± 0.04BCb8.76 ± 0.90Aa9.90 ± 0.42CDa
      DALZ 13092.07 ± 0.24ABCc8.89 ± 0.13Ab15.68 ± 1.43Aa
      DALZ 17011.39 ± 0.06Cc6.58 ± 0.41Ab7.92 ± 0.07Da
      DALZ 17132.79 ± 0.19Ac9.33 ± 0.28Ab12.86 ± 0.72ABCa
      Diamond1.81 ± 0.02BCc7.58 ± 0.33Ab10.78 ± 0.36CDa
      Innovation1.77 ± 0.15BCc9.46 ± 1.02Ab14.92 ± 0.56ABa
      Palisades2.45 ± 0.37ABc8.84 ± 1.12Ab12.19 ± 0.30BCa
      Cl−
      Lazer7.55 ± 0.30Ac9.72 ± 0.56Db14.00 ± 0.28Ba
      DALZ 13095.65 ± 0.23Ab12.20 ± 0.02BCDb23.97 ± 2.84Aa
      DALZ 17015.67 ± 0.22Ac9.68 ± 0.68Db13.25 ± 0.77Ba
      DALZ 17136.55 ± 0.10Ac13.75 ± 0.31ABCb19.15 ± 0.40ABa
      Diamond6.43 ± 0.10Ac11.52 ± 0.10CDb15.38 ± 0.15Ba
      Innovation5.72 ± 0.41Ac14.88 ± 0.75ABb25.18 ± 1.45Aa
      Palisades7.27 ± 0.99Ab15.97 ± 1.36Aa18.87 ± 0.96ABa
      Means and standard errors are presented (n = 8). Different letters indicate significant differences Tukey's HSD test; uppercase among genotypes and lowercase among treatments.
    DISCUSSION

    • Throughout the study, although the salt treatments remained fixed, salt accumulation occurred in the substrate as indicated by the increase in leachate EC of the salt treatments. Salt accumulation in the substrate depends on many factors, including salinity of the irrigation water, irrigation frequency, leaching fraction, and substrate type. The leaching fraction, simplified, is the percent of irrigation that drains out of the substrate[25]. Higher leaching fractions can flush ions, including Na+ and Cl−, away from the root zone and out of the substrate. In this study, a leaching fraction of approximately 35% was applied to slow down the accumulation of salts in the substrate without wasting too much irrigation. Despite this, leachate EC increased throughout the study, most notably in the EC10 treatment. This imposed additional osmotic and/or ionic stress on the grasses beyond the fixed treatment salinities of 5.0 and 10 dS m−1. Nevertheless, this is representative of irrigation regiments in arid landscaping, where low irrigation volumes and leaching fractions are commonly applied[26].

      Biomass was reduced by the high salt treatment more notably in the root tissue compared to the shoot tissue. In fact, shoot tissue increased marginally relative to the control in most genotypes when treated with salt, which is indicative of salt tolerance and halophytes[24]. However, root tissue sensitivity to salt stress is rather unique, since typically shoot tissue is more sensitive[10]. Chavarria et al.[1] observed both increases and reductions in root mass among eight turfgrass genotypes when treated with 15 and 30 dS m−1 salinity, when compared to the control. Additionally, in the present study the cluster analysis based on shoot and root tissue biomass identified the genotypes DALZ 1309, DALZ 1713, and Diamond as the most salt tolerant, which corresponds with the relative root tissue DW in the EC5 treatment. Therefore, our results indicate that root tissue biomass in turfgrasses might be a greater indication of salinity tolerance than shoot tissue biomass. This could be because grasses have relatively small leaf surface area and large root/shoot ratios compared to other plants[27].

      Salt tolerance for ornamental crops not only depends on growth under saline conditions, but also visual appearance, as salinity can impose ionic stress to plants which can lead to leaf burn[12]. For turfgrasses, this is especially true due to its primary use for aesthetics and environmental benefits in residential, recreational, or commercial landscaping[28]. For turfgrass managers, greenness can be a more important trait than shoot yield. Marcumm & Pessarakli[29] reported GLA ranges of 7% to 84% in eight Distichlis spicata turfgrass genotypes treated with up to 1.0 mol L−1 (58.5 g L−1) NaCl for one week. In the present study, our results indicate relatively high GLA and hence, excellent visual quality in most genotypes even when treated with high (EC10) salinity for eight weeks. In contrast, the significant reductions in GLA in the genotype DALZ 1309 in the EC10 treatment indicates less salt tolerance and susceptibility to ionic stress.

      Continued growth under saline conditions is another desirable trait in turfgrasses, indicating long-term establishment. However, mowing is a necessary management practice for turfgrass and has been shown to affect the salinity tolerance of turfgrass varieties. For example, clipping yield of creeping bentgrass (Agrostis palustris) was reduced the most under low mowing height (6.4 mm) compared to high mowing height (25.4 mm), when treated with salinity ranging from 5 to 15 dS m−1[30]. Similarly, our results showed that high salinity (EC10) reduced clipping DW compared to the control at a mowing height of 2.0 cm. However, at the end of the study, clipping DW tended to decline in the EC10 treatment in the genotypes DALZ 1701, Innovation, and Palisades, indicating less tolerance to salinity at this mowing height, whereas the remaining genotypes showed marginal gains in clipping DW, most notably Diamond, indicating greater tolerance to salinity at the respective mowing height.

      A key mechanism of salt tolerance in plants is the ability to exclude Na+ and Cl− from the leaf tissue by various means, such as sequestration in the cell vacuole or excretion through specific glands in the leaf[6]. Therefore, concentration of salts in the shoot tissue can be an indication of salt tolerance and/or mechanisms of salinity tolerance in a specific plant. In the present study, Na+ and Cl− concentrations in the shoot tissue increased in all genotypes when treated with high salt (EC10), indicating salt accumulation in the shoot tissue. However, our results also showed genotypic variation in salt accumulation, indicating different mechanisms for dealing with the salts. For example, genotype DALZ 1701 had the lowest concentration of Na+ which correlated with its excellent visual and growth parameter, and a potential explanation for this is it could more affectively exclude Na+ or excrete it from the leaves, which could contribute to its excellent visual quality (high GLA) and overall good salt tolerance in the present study. Chavarria et al.[1] reported Na+ concentrations in the shoot tissue ranging from 7.2 to 22.4 mg g−1 of eight warm-season turfgrasses when treated with 15 dS m−1, which were comparable values to those reported here considering the higher salt treatment. However, they also reported that salt excretion correlated with salt tolerant genotypes. Nevertheless, the ability to maintain high Na+ and Cl− concentrations in the shoot tissue while maintaining good visual quality and growth, indicates tolerance to osmotic and ionic salinity stress, which our results demonstrated.

    CONCLUSIONS

    • Our results primarily indicated genotypic variation present within zoysiagrasses for the improvement of salt tolerance. The genotypes Zoysia matrella 'Diamond', Z. japonica 'Palisades', three Z. matrella x Z. japonica hybrids (DALZ 1701, DALZ 1713, and 'Innovation'), and two Z. minima × Z. matrella hybrids (DALZ 1309 and 'Lazer') showed variation in potential for use in landscaping with saline irrigation in arid regions for the purpose of conserving freshwater resources and maintaining aesthetic and environmental benefits of green groundcover. Based on the growth, visual quality (GLA), and physiological results of this study, the genotypes Diamond and DALZ 1713 exhibited superior salt tolerance across multiple growth and physiological traits evaluated while DALZ 1701 expressed potential for improved salinity tolerance from its ability to exclude salt and maintain high visual quality.

      Acknowledgments

      • Funding for this project is provided by USDA NIFA to Project No. 2017-68007-26318, through the Agriculture and Food Research Initiative, Water for Agricultural Challenge Area, and hatch project TEX07726.

      Conflict of interest

      • The authors declare that they have no conflict of interest.

      Supplementary information
      • Supplemental Fig. S1 Photos of the seven genotypes that were treated for 8 weeks: control (left), EC5 (middle), and EC10 (right). The genotype arrangement in each treatment was randomized. Photos were taken right after trimming.
      Rights and permissions
      • Copyright: © 2022 by the author(s). Published by Maximum Academic Press, Fayetteville, GA. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
    Figure (4)  Table (3) References (30)
  • About this article
    Cite this article
    Hooks T, Masabni J, Ganjegunte G, Sun L, Chandra A, et al. 2022. Salt tolerance of seven genotypes of zoysiagrass (Zoysia spp.). Technology in Horticulture 2:8 doi: 10.48130/TIH-2022-0008
    Hooks T, Masabni J, Ganjegunte G, Sun L, Chandra A, et al. 2022. Salt tolerance of seven genotypes of zoysiagrass (Zoysia spp.). Technology in Horticulture 2:8 doi: 10.48130/TIH-2022-0008
    shu

Catalog

  • Html

  • Introduction
  • Materials and methods

  • Plant material and culture

  • Saline treatments

  • Greenhouse environment

  • Data collection

  • Statistical analysis

  • Results

  • Leachate electrical conductivity (ec)

  • Relative tissue dry weight (dw)

  • Hierarchal cluster analysis

  • Green leaf area (gla) index

  • Clipping dry weight (dw)

  • Tissue sodium and chloride content

  • Discussion
  • Conclusions
  • Acknowledgments
  • Conflict of interest
  • Supplementary information
  • Rights and permissions
  • About this article
logo

Contents

Policies

Services

Partnerships

© 2025 Maximum Academic Press, except Open Access articles. MAP is a member of ALPSP, COPE, CrossRef, cOAlition S, OASPA and STM.

Privacy Policy  |  Site Map  |  Terms and Conditions

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return