Search
Submit Manuscript
2.8CiteScore
Advanced Search
MAP  >  Emergency Management Science and Technology
2024 Volume 4
Article Contents
Abstract
Introduction
Materials and methods
Results
Discussion
Conclusions
Author contributions
Data availability
Acknowledgments
Conflict of interest
Rights and permissions
References
About this article
Next Previous
ARTICLE   Open Access    

Experimental study on the influence of material width on discrete fire spread in open space

  • 1.

    School of Safety Engineering, China University of Mining and Technology, Xuzhou 221116, China

  • 2.

    Yunlong Lake Deep Earth Science and Engineering Laboratory , Xuzhou 221116, China

  • 3.

    School of Safety Engineering, Changzhou University, Changzhou 213164, China

More Information
  • This study addresses the significant fire hazards associated with using thermoplastic materials, particularly PMMA (poly methyl methacrylate), which are prone to flammability and high calorific values. By employing a methodology that combines small-scale experiments and theoretical analysis, this paper investigates the impact of material width on the behavior of discrete flames in open spaces, using specimens ranging from 5 to 10 cm in width. The findings indicate that an increase in specimen width positively affects the burning area and brightness, while the dimensionless flame height and heat release rate per unit width exhibit a negative power law decay with increasing width. This suggests that beyond a critical width, further increases in width have little influence on flame propagation. The results of this study contribute to a better understanding of fire dynamics in thermoplastics and provide valuable insights that could lead to enhanced fire safety standards and material designs. The originality of this research lies in its detailed analysis of how material dimensions influence flame behavior, a topic that has not been extensively explored before, offering significant practical value in applications where fire safety is crucial.

  • Introduction

    Scale insects (Hemiptera: Coccomorpha) with hypogeic habits are considered of high phytosanitary relevance for coffee crops (Rubiaceae: Coffea spp.) in Colombia[1]. A total of 65 species of scale insects associated with coffee roots have been recorded in Colombia[2−4]. The most species-rich family is the Pseudococcidae with 28 species distributed in nine genera: Dysmicoccus Ferris, 1950 (13 spp.), followed by Pseudococcus Westwood, 1840 (four spp.), Phenacoccus Cockerell, 1893 (three spp.), Planococcus Ferris, 1950, and Spilococcus Ferris, 1950 (two spp. each), and Chorizococcus McKenzie, 1960, Distichlicoccus Ferris, 1950, Ferrisia Fullaway, 1923, and Paraputo Laing, 1929 (one sp. each). For the family Rhizoecidae, 19 species have been recorded in six genera, namely, Rhizoecus Kunckel d'Herculais, 1878 (13 spp.), Pseudorhizoecus Green, 1933 (two spp.), and Capitisetella Hambleton, 1977, Coccidella Hambleton, 1946, Geococcus Green, 1902, and Ripersiella Tinsley, 1899 (one sp. each). Other minor families include Coccidae and Ortheziidae (five spp. in each family), Xenococcidae (three spp.), and Putoidae and Diaspididae (two spp. in each family) and Margarodidae (one sp.). For this study all previous records were re-analysed with the purpose of providing an accurate list of species

    The taxonomic identification of scale insects by a morphological approach is particularly difficult, mainly for two reasons. First, they are small insects (usually < 5 mm) that require the preparation of slide-mounted specimens. Second, the taxonomic keys needed for morphological identifications are primarily designed for adult female specimens[5]. Differing from other insect orders (e.g., Coleoptera, Diptera and Hymenoptera), female scale insects lack well-defined tagmata, as well as sclerites, sutures, or discernible areas. Characters of taxonomic value in scale insects include cuticular processes, such as pores, ducts and, setae[5]. Recognizing these cuticular structures on such small bodies poses a difficult task for non-expert entomologists. To facilitate accessible identification, this manuscript offers an illustrated taxonomic key to scale insect species associated with coffee roots in Colombia and is aimed at users with basic knowledge of scale insect morphology.

    Materials and methods

    A careful revision of the specimens studied by Caballero et al.[2], preserved in the Scale Insect Collection at the Entomological Museum 'Universidad Nacional Agronomía Bogota' UNAB (Bogotá, Colombia), was carried out to exclude species that are doubtfully recorded from coffee roots in Colombia. This re-assessment allowed the compilation of an accurate list of species that could be included in the taxonomic key. Additional species and information from Caballero[3] and Caballero et al.[4] also were used for construction of the key. List of species recorded for Colombia and c ollection data of specimens analized are in Supplemmental Table S1 and S2 respectivately.

    The illustrated taxonomic key (Table 1) is based on the external morphology of the adult female with a dichotomous structure. Each couplet after the first one is numbered followed by the number of the preceding couplet in parenthesis, e.g. 12(7) means that couplet 12 is derived from couplet 7; the numbers at the end of the couplet indicate the next couplet in order to arrive at the species name that best matches the character states selected by the user. It is illustrated in most of the steps using microphotographs. Acquisition and analysis of images were done with a Lumenera 1-5C camera and the software Image Pro Insight 8.0. Designs were performed with Affinity Photo V 2.1 and Affinity Designer V 2.1 software. The taxonomic keys were structured with some adaptations of published taxonomic keys[6−15]. The general morphological terminology follows Kondo & Watson[5] with specific terminology for Coccidae[6,16], Margarodidae[17], Ortheziidae[7], Diaspididae[18], Pseudococcidae, Putoidae[8,9], and Rhizoecidae[10,11]. The abdominal segmentation is given as SabdI for abdominal segment 1 to SabdVIII for abdominal segment 8. All microphotographs are of adult female scale insects or their taxonomically important morphological structures.

    Table 1.  Illustrated taxonomic key.
    No.DetailsRef.
    1Abdominal spiracles present (Fig. 1a)2
    −Abdominal spiracles absent (Fig. 1b)7
    Fig. 1 Abdominal spiracles (sp) on margin (a) present on Eurhizococcus colombianus, (b) absent on Distichlicoccus takumasai.
    2(1)Anal aperture without pores and setae (Fig. 2a); legs shorter than half of the transversal diameter of body (Fig. 2b); eyespots and mouthparts absentEurhizococcus colombianus

    Jakubski, 1965
    −Anal aperture forming a well-developed anal ring with pores and setae (Fig. 2c); legs longer than transversal diameter of body; eyespots and mouthparts present (Fig. 2d)
    3
    Fig. 2 Eurhizococcus colombianus: (a) Anal aperture without pores and setae in the border, (b) section of mid body showing the length of hind leg (lel) and transversal body line (btl). Insignorthezia insignis: (c) Anal aperture with pores (po) and setae (st), (d) section of head with protruding eyespot (es) and labium (lb).
    3(2)Antennae each with eight segments (Fig. 3a)4
    −Antennae each with fewer than five segments (Fig. 3b)5
    Fig. 3 (a) Eight-segmented antenna. (b) Four-segmented antenna.
    4(3)Transversal bands of spines absent in ventral region surrounded by an ovisac band (Fig. 4a); dorsal interantennal area without sclerosis (Fig. 4b)Insignorthezia insignis (Browne, 1887)
    −Transversal bands of spine plates present in ventral region surrounded by an ovisac band (Fig. 4c); longitudinal sclerosis on dorsum in interantennal area (Fig. 4d)Praelongorthezia praelonga (Douglas, 1891)
    Fig. 4 Insignorthezia insignis: (a) Abdomen without transversal clusters of wax plates, (b) Dorsal interantennal area without sclerosis. Praelongorthezia praelonga: (c) Abdomen with transversal clusters of wax plates marked by dash lines, (d) dorsal interantennal area with a longitudinal sclerotic plate (ep).
    5(3)Antennae each with three segments (Fig. 5a)Newsteadia andreae Caballero, 2021
    −Antennae each with four segments (Fig. 5b)6
    Fig. 5 (a) Three-segmented antenna of Newsteadia andreae. Note the presence of pseudosegmentation which gives the appearance of additional segments in the last antennal segment. (b) Four-segmented antenna of Mixorthezia minima.
    6(5)Dorsal area anterior to anal ring with simple pores on protuberances (Fig. 6a); ventral areas surrounding each coxa with a row of wax plate spines (Fig. 6b)Mixorthezia minima Koczné Benedicty & Kozár, 2004
    −Dorsal area anterior to anal ring without simple pores or protuberances (Fig. 6c); ventral areas posterior to each coxa without wax plate spines (Fig. 6d)Mixorthezia neotropicalis (Silvestri, 1924)
    Fig. 6 Mixorthezia minima: (a) Dorsum of area anterior to anal ring with close-up of simple pores on protuberances (dash box); (b) ventral area posterior to each coxa with a row of wax plate spines (dash box). Mixorthezia neotropicalis: (c) Close-up of dorsum of area anterior to anal ring lacking simple pores on protuberances (dash box); (d) ventral area posterior to each coxa without associated wax plate spines.
    7(1)Anal plates present (Fig. 7a)8
    −Anal plates absent (Fig. 7b)12
    Fig. 7 (a) Anal apparatus of Saissetia coffeae with anal plates (ap) covering the anal aperture (aa). (b) Anal apparatus of Pseudococcus sp. with anal aperture lacking anal plates.
    8(7)Antennae and legs with length similar to or shorter than spiracles (Fig. 8a)9
    −Antennae and legs with length at least twice as long as spiracles (Fig. 8b)11
    Fig. 8 (a) Antenna (an) and foreleg (lg) (green lines), and anterior spiracle (sp) (yellow line) of Toumeyella coffeae showing their relative length. Note the similar size of the limbs and spiracle. (b) Antenna (an) and leg (lg) (green lines), and anterior spiracle (sp) (yellow line) of Coccus viridis showing their relative length. Note the relatively smaller size of the spiracle.
    9(8)Ventral tubular macroducts present (Fig. 9)Toumeyella coffeae
    Kondo, 2013
    −Ventral tubular macroducts absent10
    Fig. 9 Ventral tubular macroducts (dash box) and close-up of macroducts (photo on right side).
    10(9)Orbicular pores (Fig. 10a) and cribriform platelets present (Fig. 10b); dorsal setae absent; opercular pores absentCryptostigma urichi (Cockerell, 1894)
    −Orbicular pores and cribriform platelets absent; dorsal setae present (Fig. 10c); numerous opercular pores present throughout mid areas of dorsum (Fig. 10d)Akermes colombiensis Kondo & Williams, 2004
    Fig. 10 Cryptostigma urichi: (a) Orbicular pore and (b) close-up of a cribriform platelet. Akermes colombiensis: (c) Close-up of a dorsal body setae (dash box) and (d) close-up of opercular pores (arrows).
    11(8)Band of ventral tubular ducts in lateral and submarginal regions absent, ventral tubular ducts of one type; anal plates without discal setae (Fig. 11a); dorsal body setae capitate or clavate (Fig. 11b); perivulvar pores with seven or eight loculi, rarely with 10 loculi (Fig. 11c)Coccus viridis
    (Green, 1889)
    −Band of ventral tubular ducts in lateral and submarginal regions present, submarginal region with two types of tubular ducts (Fig. 11d); anal plates with discal setae (Fig. 11e); dorsal body setae spine-like, apically pointed (Fig. 11f); perivulvar pores mostly with 10 loculi (Fig. 11g)Saissetia coffeae
    (Walker, 1852)
    Fig. 11 Coccus viridis: (a) Anal plates without discal setae; (b) dorsal body setae capitate (top) or clavate (below); (c) multilocular disc pores mostly with eight loculi. Saissetia coffeae: (d) Ventral submarginal region with two types of tubular ducts; (e) each anal plate with a discal seta; (f) dorsal body setae acute; (g) multilocular disc pores with mostly 10 loculi.
    12(7)Cerarii present on body margin, at least a pair on each anal lobe (Fig. 12a)13
    −Cerarii absent on body margin (Fig. 12b)38
    Fig. 12 Abdominal body margin of (a) Pseudococcus sp. with three cerarii (dash box) and (b) Rhizoecus sp. (dash box) without cerarii.
    13(12)Enlarged oral collar tubular ducts composed of a sclerotized area surrounding the border and a set of flagellated setae (Ferrisia-type oral collar tubular ducts) (Fig. 13a)Ferrisia uzinuri
    Kaydan & Gullan, 2012
    −Oral collar tubular ducts simple, not as above (Fig. 13b) or absent14
    Fig. 13 (a) Ferrisia-type oral collar tubular ducts with aperture of tubular duct (ad) surrounded by a sclerotized area (sa) and associated flagellate setae (fs). (b) Oral collar tubular ducts simple (arrows).
    14(12)Antenna with nine segments (Fig. 14a)15
    −Antenna with eight segments (Fig. 14b) or fewer (Fig. 14c)19
    Fig. 14 Antenna with (a) nine segments, (b) eight segments and (c) seven segments.
    15(14)Cerarii with more than five conical setae (Fig. 15a); hind trochanter with six sensilla, three on each surface (Fig. 15b)16
    −Cerarii with two lanceolate setae (Fig. 15c); hind trochanter with four sensilla, two on each surface (Fig. 15d)17
    Fig. 15 Puto barberi: (a) upper and lateral view of a cerarius, (b) close-up of the surface of trochanter with three sensilla (arrows). Phenacoccus sisalanus: (c) cerarius, (d) trochanter with two sensilla (arrows) on single surface.
    16(15)Cerarii with tubular ducts (Fig. 16a)Puto antioquensis
    (Murillo, 1931)
    −Cerarii without tubular ducts (Fig. 16b)Puto barberi
    (Cockerell, 1895)
    Fig. 16 (a) Cerarius associated with tubular ducts (arrows). (b) Cerarius without tubular ducts.
    17(15)Oral collar tubular ducts absentPhenacoccus sisalanus Granara de Willink, 2007
    −Oral collar tubular ducts present, at least on venter (Fig. 17)18
    Fig. 17 Ventral surface with oral collar tubular ducts (dash circles).
    18(17)Oral collar tubular ducts restricted to venterPhenacoccus solani
    Ferris, 1918
    −Oral collar tubular ducts present on dorsum and venterPhenacoccus parvus Morrison, 1924
    19(14)Oral rim tubular ducts present (Fig. 18)20
    −Oral rim tubular ducts absent26
    Fig. 18 Oral rim tubular ducts in upper view (dash circles) and close-up of lateral view.
    20(19)Oral rim tubular ducts present on venter onlyPseudococcus landoi (Balachowsky, 1959)
    −Oral rim tubular ducts present on both dorsum and venter21
    21(20)Cerarii restricted to anal lobes (Fig. 19a)Chorizococcus caribaeus Williams & Granara de Willink, 1992
    −Cerarii present, at least on the last five abdominal segments (Fig. 19b)22
    Fig. 19 Location of cerarii (dash boxes) on abdominal margin with close-up of cerarius (a) restricted to anal lobes (dash boxes) and (b) cerarii present on the last five abdominal segments.
    22(21)Circulus absent (Fig. 20a)23
    −Circulus present (Fig. 20b)24
    Fig. 20 Ventral mid area of abdominal segments III and IV (dash box) of (a) Distichlicoccus takumasai without circulus and (b) Pseudococcus jackbeardsleyi with circulus.
    23(22)Multilocular disc pores present on venter of SabdIV and posterior segments (Fig. 21a); hind coxa with translucent pores and hind femur without translucent pores (Fig. 21b)Spilococcus pressus
    Ferris, 1950
    −Multilocular disc pores absent, if some present, not more than three around vulvar opening (i.e. venter of SabdVII or SabdVIII); hind coxa without translucent pores (Fig. 21c) and hind femur with translucent pores (Fig. 21d)Distichlicoccus takumasai Caballero, 2021
    Fig. 21 Spilococcus pressus: (a) Ventral section of abdomen with multilocular disc pores (arrows); (b) hind leg with close-up of coxa with translucent pores (arrows). Distichlicoccus takumasai: (c) Hind coxa without translucent pores; (d) hind femur with translucent pores (arrows).
    24(22)Eyes without discoidal pores nor sclerotized surrounding area (Fig. 22a); circulus with transversal diameter 40 to
    60 µm (Fig. 22b)    		Pseudococcus luciae Caballero, 2021
    −Eyes with discoidal pores and sclerotized surrounding area (Fig. 22c); circulus diameter 100 to 200 µm (Fig. 22d)26
    25(24)Oral rim tubular ducts on dorsal abdominal segments numbering three to eight; area between posterior ostiole and cerarius of SabdVII without oral rim tubular ducts (Fig. 23a)Pseudococcus elisae Borchsenius, 1947
    −Oral rim tubular ducts on dorsal abdominal segments numbering 14 to 27; area between posterior ostiole and cerarius of SabdVII with an oral rim tubular duct (Fig. 23b)Pseudococcus jackbeardsleyi Gimpel & Miller, 1996
    Fig. 22 Pseudococcus luciae: (a) Eyespot without surrounding sclerotized area nor associated pores; (b) circulus ca. 58 µm wide. Pseudococcus jackbeardsleyi: (a) Eyespot with sclerotized area (sa) and associated pores (po); (d) circulus ca. 154 µm wide.
    Fig. 23 (a) Dorsal margin of abdominal segments VI to VIII, between cerarius of anal lobe (C1), cerarius of SabdVII (C2) and posterior ostiole (os) without oral rim tubular ducts. (b) Dorsal margin of abdominal segments VI to VIII, between cerarius of anal lobe (C1), cerarius of SabdVII (C2) and posterior ostiole (os) with an oral rim tubular duct and/or cerarius adjacent to SabdVII.
    26(19)Oral collar tubular ducts (Fig. 24) on both dorsum and venter27
    −Oral collar tubular ducts restricted to venter28
    Fig. 24 Oral collar tubular duct in lateral view.
    27(26)Hind coxa with translucent pores (Fig. 25a); anal lobe with sclerotized bar, not on a sclerotized area (Fig. 25b); multilocular disc pores present posterior to fore coxaPlanococcus citri-minor complex
    −Hind coxa without translucent pores (Fig. 25c); anal lobe without sclerotized bar, on a sclerotized area (Fig. 25d); multilocular disc pores absent posterior to fore coxaDysmicoccus quercicolus (Ferris, 1918)
    28(27)Oral collar tubular ducts absent on venter of both head and thorax.29
    −Oral collar tubular ducts present on either head or thorax, but not on both areas (Fig. 26)30
    Fig. 25 Planococcus citri-minor complex: (a) Hind coxa with translucent pores (dash box) and (b) anal lobe with a sclerotization forming a bar (ab). Dysmicoccus quercicolus: (c) Hind coxa without translucent pores and (d) anal lobe with irregular broad sclerotized area (sa).
    Fig. 26 Marginal area of Dysmicoccus grassii, lateral to posterior spiracle (ps), with close-up of oral collar tubular ducts (oc) (left side).
    29(28)Translucent pores present on hind coxa, trochanter, femur and tibia (Fig. 27a); marginal clusters of oral collar tubular ducts on venter of SabdVI and SabdVIIDysmicoccus caribensis Granara de Willink, 2009
    −Translucent pores restricted to hind femur and tibia (Fig. 27b); marginal clusters of oral collar tubular ducts present on venter of SabdIV to SabdVIIParaputo nasai
    Caballero, 2021
    Fig. 27 (a) Hind leg of Dysmicoccus caribensis with translucent pores on coxa (cx), trochanter (tr) and femur (fm), and tibia (tb). (b) Hind leg of Paraputo nasai with translucent pores restricted to femur (fm) and tibia (tb).
    30(28)Hind coxa with translucent pores (Fig. 28a)Dysmicoccus sylvarum
    Williams & Granara de Willink, 1992
    −Hind coxa without translucent pores (Fig. 28b)31
    Fig. 28 (a) Translucent pores on hind coxa. (b) Translucent pores absent on hind coxa.
    31(30)Hind trochanter with translucent pores (Fig. 29a)Dysmicoccus varius
    Granara de Willink, 2009
    −Hind trochanter without translucent pores (Fig. 29b)32
    Fig. 29 Translucent pores (a) on hind trochanter, (b) absent from hind trochanter.
    32(31)Oral collar tubular ducts present on margin of thorax (Fig. 30)33
    −Oral collar tubular ducts absent from margin of thorax34
    Fig. 30 Prothorax margin of Dysmicoccus grassii with close-up of oral collar tubular ducts.
    33(32)Multilocular disc pores absent on SabdV; dorsal area immediately anterior to anal ring with tuft of flagellate setae; longest flagellate seta as long as diameter of anal ring (Fig. 31a), and discoidal pores larger than trilocular pores (Fig. 31b)Dysmicoccus radicis
    (Green, 1933)
    −Multilocular disc pores present on SabdV; dorsal area immediately anterior to anal ring without a tuft of flagellate setae; flagellate setae much shorter than diameter of anal ring (Fig. 31c) and discoidal pores smaller than trilocular pores (Fig. 31d)Dysmicoccus grassii (Leonardi, 1913)
    34(32)Oral collar tubular ducts absent in interantennal area35
    −Oral collar tubular ducts present in interantennal area (Fig. 32)36
    35(34)Translucent pores on hind leg restricted to tibia (Fig. 33a)Dysmicoccus perotensis
    Granara de Willink, 2009
    −Translucent pores on hind leg present on tibia and femur (Fig. 33b)Dysmicoccus joannesiae-neobrevipes complex
    Fig. 31 Dysmicoccus radicis: (a) Area anterior to anal ring with a cluster of flagellate setae (fs) and anal ring (ar) showing the diameter of the different pores (dash box); (b) discoidal pores (dp) and trilocular pores (tp). Dysmicoccus grassii: (c) Area anterior to anal ring with scattered short flagellate setae (fs) contrasted with anal ring (ar) diameter (dash box); (d) discoidal pores (dp) and trilocular pores (tp) with similar diameter.
    Fig. 32 Interantennal area (dash box) of Dysmicoccus brevipes with close-up of oral collar tubular ducts.
    Fig. 33 (a) Hind leg of Dysmicoccus perotensis with close-up of femur and tibia with translucent pores on tibia only (arrows). (b) Hind leg of Dysmicoccus joannesiae-neobrevipes complex with close-up of femur and tibia with translucent pores (arrows).
    36(34)Hind coxa with translucent pores (see Fig. 28a)Dysmicoccus mackenziei
    Beardsleyi, 1965
    −Hind coxa without translucent pores (see Fig. 28b)37
    37(36)Dorsal SabdVIII setae forming a tuft-like group, each seta conspicuously longer than remaining dorsal abdominal setae (Fig. 34a) and setal length similar to anal ring diameter (60–80 µm long)Dysmicoccus brevipes (Cockerell, 1893)
    −Dorsal SabdVIII setae evenly distributed, each setae as long as remaining dorsal abdominal setae (Fig. 34b) and length less than half diameter of anal ringDysmicoccus texensis-neobrevipes complex
    38(12)Tritubular ducts absent39
    −Tritubular ducts present (Fig. 35a-b)46
    Fig. 34 (a) Abdomen of Dysmicoccus brevipes with dorsal setae on SabdVIII (lfs) longer than setae on anterior segments (sfs). (b) Abdomen of Dysmicoccus texensis-neobrevipes complex with dorsal setae (ufs) along the abdominal segments of uniform length and scattered distribution.
    Fig. 35 (a) Tritubular duct in upper (left) and lateral view (right) with the border of the cuticular ring attached to tubules. (b) Tritubular duct with the border of the cuticular ring widely separated from tubules (arrows).
    39(38)Anal lobes strongly protruded, bulbiform (Fig. 36a) jutting out from margin for a distance equivalent to diameter of anal ring40
    −Anal lobes shallow, if protruded, their length never more than half of diameter of anal ring (Fig. 36b)42
    Fig. 36 (a) Abdomen of Neochavesia caldasiae with anal lobes (al) protruding beyond the anal aperture (aa). (b) Abdomen of Ripersiella sp. with anal lobes (al) at the same level as the anal aperture (aa).
    40(39)Anal aperture located at the same level as the base of anal lobes (Fig. 37a); antennae located on ventral margin of headNeochavesia caldasiae (Balachowsky, 1957)
    −Anal aperture located anterior to bases of anal lobes (Fig. 37b); antennae located on dorsum of head41
    Fig. 37 (a) Abdomen of Neochavesia caldasiae with anal aperture (aa) positioned between the anal lobes (al), at the same level as the bases of anal lobes (dash line). (b) Abdomen of Neochavesia eversi with anal aperture (aa) situated anterior to the bases of the anal lobes (al) (dash line).
    41(40)Antennae each with five segments, situated on a membranous base (Fig. 38a); length of hind claw less than length of hind tarsus (Fig. 38b)Neochavesia trinidadensis (Beardsley, 1970)
    −Antennae each with four segments, situated on a sclerotized base (Fig. 38c); hind claw longer than hind tarsus (Fig. 38d)Neochavesia eversi (Beardsley, 1970)
    Fig. 38 (a) Antenna with four segments and a membranous base (mb). (b) Hind tarsus (green line) longer than the hind claw (red line). (c) Antenna with four segments and a sclerotized base (sb). (d) Hind tarsus (green line) shorter than hind claw (red line).
    42(39)Body setae capitate, at least on one surface (Fig. 39a)43
    −Body setae never capitate (Fig. 39b)44
    Fig. 39 (a) Capitate setae. (b) Flagellate setae.
    43(42)Anal aperture without associated cells (Fig. 40a); three-segmented antennae (Fig. 40b); ventral setae in median
    and submedian regions capitate    		Capitisitella migrans
    (Green, 1933)
    −Anal aperture surrounded by cells (Fig. 40c); six-segmented antennae (Fig. 40d); ventral setae in medial and submedial regions flagellateWilliamsrhizoecus coffeae
    Caballero & Ramos, 2018
    44(42)Three-segmented antennae (Fig. 41a); circulus present (Fig. 41b)Pseudorhizoecus bari
    Caballero & Ramos, 2018
    −Five-segmented antennae (Fig. 41c); circulus absent45
    Fig. 40 Capitisitella migrans: (a) Anal aperture of surrounded only by setae; (b) antenna composed of three segments. Williamsrhizoecus coffeae: (c) Anal aperture of surrounded by setae and cells (flesh); (d) antenna composed of six segments.
    Fig. 41 Pseudorhizoecus bari: (a) Antenna composed of three segments and (b) circulus. (c) Antenna of Pseudorhizoecus proximus composed of five segments.
    45(44)Multilocular disc pores absent; anal aperture ornamented with small protuberances and two to five short setae, each seta never longer than 1/3 diameter of anal aperture, without cells (Fig. 42a)Pseudorhizoecus proximus
    Green, 1933
    −Multilocular disc pores present (Fig. 42b); anal aperture not ornamented with small protruberances, ring with well-developed cells and six long setae, each seta as long as diameter of anal ring (Fig. 42c)Ripersiella andensis (Hambleton,
    1946)
    Fig. 42 (a) Anal aperture of Pseudorhizoecus proximus surrounded by protuberances (pr) and a few short setae (st). Ripersiella andensis: (b) Ventral section of abdomen with multilocular disc pores (mp); (c) anal aperture with a ring of cells and six long setae (se).
    46(38)Anal lobes strongly protruded, conical, each one with a stout spine at apex (Fig. 43a)Geococcus coffeae
    Green, 1933
    −Anal lobes flat or barely protruded, without spines at apex (Fig. 43b)47
    47(46)Venter of abdomen with clusters of trilocular pores in medial region (Fig. 44a)Coccidella ecuadorina Konczné Benedicty & Foldi, 2004
    −Venter of abdomen with trilocular pores evenly dispersed, never forming clusters in medial region (Fig. 44b)48
    Fig. 43 (a) Abdomen of Geococcus coffeae with protruding anal lobe (al) with a stout spine at the apex (sp). (b) Abdomen of Rhizoecus sp. with anal lobe (al) flat, with numerous flagellate setae (fs) at the apex.
    Fig. 44 (a) Ventral surface of Coccidella ecuadorina with clusters of trilocular pores (tc) (dash box) on medial region of abdomen. (b) Ventral surface of Rhizoecus sp. with trilocular pores (tr) scattered on venter of abdomen.
    48(47)Antennae with six well-developed segments (Fig. 45a)51
    −Antennae with five well-developed segments (Fig. 45b), apical segment sometimes partially divided (Fig. 45c)49
    Fig. 45 (a) Six-segmented antenna. (b) Five-segmented antenna. (c) Five-segmented antenna with partially divided apical segment (pd). Note: antennal segments numbered in Roman numerals.
    49(48)Antennae length more than 140 µm (Fig. 46a); tritubular ducts of similar diameter to trilocular pores (± 2 µm variation) (Fig. 46b); tritubular ducts with space between ductules and edge as wide as the ductules (Fig. 46c); slender ductule, width/length ratio 1:6Rhizoecus coffeae
    Laing, 1925
    −Antennae length less than 130 µm (Fig. 46d); tritubular ducts of diameter nearly twice diameter of trilocular pores (Fig. 46e); tritubular ducts with reduced space or without space between ductules and edge (Fig. 46f); stout ductule, width/length ratio 1:350
    50(49)Tubular ducts present (Fig. 47a); each anal lobe with around 28 dorsal setae of similar length, greater than 30 µm (Fig. 47b, al); and dorsal marginal clusters of setae on SabdVII 20–30 µm long (Fig. 47b, SabdVII)Rhizoecus setosus (Hambleton, 1946)
    −Tubular ducts absent; each anal lobe with around 14 dorsal setae, with length less than 15 µm (Fig. 47c, al); dorsal marginal clusters of setae on SabdVII with length less 15 µm (Fig. 47c, SabdVII)Rhizoecus compotor
    Williams & Granara de Willink, 1992
    Fig. 46 (a) Antenna ca. 207 µm long. (b) Tritubular ducts (td) and trilocular pores (tp) with similar diameter. (c) Close-up of a tritubular duct indicating the space between the cuticular ring (mg) and the ductule (dt). (d) Antenna ca. 105 µm long. (e) Each tritubular duct (td) twice the diameter of a trilocular pore (tp). (f) Close-up of tritubular duct without a space between the cuticular ring (mg) and the ductule (dt).
    Fig. 47 Rhizoecus setosus: (a) Tubular ducts (td); (b) anal lobe (al) and abdominal segment (SabdVII) with marginal clusters of setae longer than 30 µm. (c) Abdomen of Rhizoecus compotor with marginal cluster of setae shorter than 20 µm on anal lobe (al) and abdominal segment (SabdVII).
    51(48)Fore tibia with at least one of two internal preapical setae spine-like (Fig. 48a-b)52
    −Fore tibia with both internal preapical setae flagellate (Fig. 48c)56
    Fig. 48 Fore legs with preapical setae on tibia (ft): (a) one flagellate (fs) and one spine seta (ss), (b) with a pair of spine setae (ss), (c) with a pair of flagellate setae (fs).
    52(51)Fore tibia with one internal preapical spine-like setae and other seta flagellate (Fig. 48a); anal ring composed of spine-like setae (Fig. 49a); circulus absentRhizoecus spinipes (Hambleton, 1946)
    −Fore tibia with both internal preapical setae spine-like (Fig. 48b); anal ring composed of flagellate-like setae (Fig. 49b); at least, one circulus present (Fig. 49c)53
    Fig. 49 (a) Anal ring (ar) of Rhizoecus spinipes with spine-like setae (ss). (b) Anal ring (ar) of Rhizoecus arabicus with flagellate setae (fs). (c) Circulus of Rhizoecus cacticans.
    53(52)Claw digitules setose and short, length less than half length of claw (Fig. 50a)54
    −Claw digitules capitate and long, as long as claw (Fig. 50b)55
    Fig. 50 Claw with claw digitule: (a) setose (sd), (b) flagellate (fd).
    54(53)Anal ring with external row composed of 35 cells or more (Fig. 51a, ext); anal ring with external and internal rows separated by a space as wide as a cell of the external row (Fig. 51a, spc); anal ring cells without spicules (Fig. 51a, sp)Rhizoecus variabilis Hambleton, 1978
    −Anal ring with external row composed of less than 30 cells (Fig. 51b, ext); anal ring with external and internal rows separated by a narrow space, as wide as half (or less) a cell of the external row (Fig. 51b, spc); anal ring cells with spicules (Fig. 51b, sp)Rhizoecus arabicus Hambleton, 1976
    Fig. 51 (a) Anal ring of Rhizoecus variabilis with external row (ext) of anal ring consisting of over 35 cells; external row separated from the internal row (int) by a similar width as the diameter of a cell (spc). (b) Anal ring of Rhizoecus arabicus with external row (ext) of anal ring with less than 30 cells; external row separated from the internal row (int) by a width less than half the diameter of a cell (spc); cells of the external row with spicules (sp).
    55(53)More than 80 tritubular ducts; circulus with basal diameter at least five times greater than apical diameter (Fig. 52a); stick-like genital chamber, parallel borders and all of similar width and structure, length across about two abdominal segments (169–175 µm long) (Fig. 52b)Rhizoecus atlanticus (Hambleton, 1946)
    −Less than 50 tritubular ducts; circulus with basal diameter less than three times the apical diameter (Fig. 52c); genital chamber with basal third two times wider than anterior two-thirds, length across one abdominal segment (43–52 µm long) (Fig. 52d)Rhizoecus cacticans (Hambleton, 1946)
    Fig. 52 Rhizoecus atlanticus: (a) Circulus with diameter at base five times the apical diameter, (b) genital chamber tubular shape, length ca. 150 µm long. Rhizoecus cacticans: (c) Circulus with diameter at base about two times the apical diameter, (d) genital chamber with proximal section basiform and distal section tubular, with arms, length ca. 45 µm long.
    56(51)Multilocular disc pores absent on dorsumRhizoecus mayanus (Hambleton, 1946)
    −Multilocular disc pores present on dorsum57
    57(56)Marginal prothoracic setae length greater than 50 µm (Fig. 53a); marginal SabdVII setae length greater than 45 µm (Fig 53b)Rhizoecus colombiensis Ramos-Portilla & Caballero, 2016
    −Marginal prothoracic setae length less than 25 µm (Fig. 53c); marginal SabdVII setae length less than 30 µm (Fig. 53d)58
    Fig. 53 Rhizoecus colombiensis: (a) Body margin with a long seta (pts) (> 40 µm), longer than remaining setae in prothorax; (b) margin of abdominal segment VII (SabdVII) (st). with a long seta (pts) (> 40 µm), longer than remaining setae in abdomen. Rhizoecus americanus: (c) Margin of prothorax (pts) with setae of uniform length, shorter than 30 µm; (d) margin of abdominal segment VII (SabdVII) with setae (st) shorter than 30 µm.
    58(57)Tritubular ducts of two sizesRhizoecus caladii
    Green, 1933
    −Tritubular ducts of three sizesRhizoecus americanus (Hambleton, 1946)
     | Show Table
    DownLoad: CSV

    Results

    The following illustrated taxonomic key (Table 1) is a tool for the identification of adult female scale insects (Hemiptera : Sternorrhyncha : Coccomorpha) associated with coffee roots in Colombia, which includes 59 species from seven families (see Supplemental Table S1).

    Discussion

    The taxonomic key includes 59 species associated with coffee roots. Hemiberlesia sp., Odonaspis sp., Rhizoecus stangei McKenzie, 1962, Spilococcus mamillariae (Bouche, 1844), Planococcus citri (Risso, 1813) and Planococcus minor (Maskell, 1897) were excluded from the key. In the case of the two armoured scale insects, the specimens were found in Berlese funnel samples associated with coffee roots[2], however, there is no evidence of these species feeding on the roots and there are no previous records of association of Hemiberlesia nor Odonaspis species with coffee roots.

    Previous records of single specimens of R. stangei and S. mamillariae by Caballero et al.[2] were determined as misidentifications of Rhizoecus caladii Green, 1933 and Spilococcus pressus Ferris, 1950, respectively. Spilococcus mamillariae is considered as an oligophagous species, but mainly associated with Cactaceae plants and feeding on the aerial parts of plants[19,20]. There are no records of S. mamillariae being found on any plant species of the family Rubiaceae, and hence we have removed this species from the list of species associated with coffee roots. The species R. stangei, which has been recorded only from Mexico and lacks information on its host plant[21] has apparently not been found since its original description[8].

    Planococcus citri and Pl. minor were listed also by Caballero et al.[2] as literature records. the morphological identification of P. citri and P. minor needs to be complemented with molecular and geographical analysis to be more accurate[22]. Therefore, the present key considers only identification to the Planococcus citri-minor complex.

    Furthermore, many specimens of Dysmicoccus collected from coffee roots in Colombia have morphological character states that overlap with Dysmicoccus neobrevipes Beardsley, 1959, Dysmicoccus joannesiae (Costa Lima, 1939) and Dysmicoccus texensis (Tinsley, 1900). The first case is a mix of character states of D. texensis and D. neobrevipes. The number of setae in the abdominal cerarii and the size of oral collar tubular ducts are the most important characters used to differentiate the adult females of Dysmicoccus species[8,23]. Adult females of D. texensis have a consistent pattern of only two setae in all thoracic and abdominal cerarii, along with a uniform size of oral collar tubular ducts (OC). On the other hand, D. neobrevipes varies in the number of setae in the cerarii, ranging from two to seven, accompanied by two distinct sizes of OC. These character states are generally constant among specimens found on the aerial parts of plants. However, among the specimens examined here, while the anal lobe cerarii consistently have two setae on the specimens of D. texensis found on the roots, the remaining cerarii display a variable number of setae, notably ranging from two to five, particularly within the abdominal cerarii. Furthermore, the OC of these specimens all are the same size. Regarding the differences in number of setae in the cerarii, Granara de Willink[23] underlined the need of more comprehensive studies to definitively separate these species.

    The second case involves D. joannesiae and D. neobrevipes. These species exhibit similarities in the number of setae on each cerarius (ranging from two to seven setae per cerarius) and differences in the number of clusters of OC along the abdominal margin; D. joannesiae has more than 25 clusters of OC and D. neobrevipes has fewer than 10 clusters of OC[8]. Granara de Willink also separated these two species by the presence of OC on the thorax and head[23] (present in D. neobrevipes and absent in D. joannesiae). Within the specimens of putative D. neobrevipes studied here, a few had clusters of OC numbering 15 to 20 along the abdominal margin and OC on the thorax and head. The primary challenge with addressing this dilemma lies in the fact that D. joannesiae has only been reported on Joannesia princeps Vell., 1798 (Euphorbiaceae) in Brazil and on Annona muricata (Annonaceae) intercepted in London from Saint Lucia[8,24]. Moreover, there has been no additional morphological variations recorded in the new records of D. joannesiae since its initial description in 1932 by Costa Lima. Therefore, the character states defining D. joannesiae are based on six type specimens. Based on these arguments, the following taxonomic key considers two species complex groups, namely the Dysmicoccus texensis-neobrevipes complex and the D. joannesiae-neobrevipes complex.

    Following article 31.1.2 of the International Commission of Nomenclature (ICZN), herein we make a change in nomenclature for Distichlicoccus takumasae Caballero, 2021. The ending -ae for takumasae is incorrect because the species was dedicated to Dr. Takumasa Kondo (a male coccidologist), and thus the correct ending is -i, hence the species epithet is herein amended to 'takumasai'. The corrected name is Distichlicoccus takumasai Caballero, 2021.

    Conclusions

    After reviewing the species of scale insects associated with coffee roots in Colombia, we have compiled a list of 59 species (Supplemental Table S1). Although this study did not focus on the effect of habit (aerial vs underground) or host plant on the morphology of scale insects, we detected significant morphological variation within facultative hypogeal species. Until further studies allow an understanding of the overlap of character states between D. texensis – D. neobrevipes and D. joannesiae – D. neobrevipes, we suggest considering these species as a morphological complex for hypogeal specimens. Further ecomorphological studies should be conducted to determine whether the morphology of a species may differ when feeding on the aerial parts compared when feeding on the underground parts of a host and to try to elucidate what factors trigger those changes, especially in species associated with coffee plants. As for the species complex, further collecting, morphological, and molecular studies should help elucidate these taxonomic problems.

    During the literature review performed for this study, we realized that most of the records of species are limited to mentioning the host but not the plant part on which collections were made, however, it is suspected that most species are normally collected from the aerial parts of the plant host. Although this taxonomic key is limited to root-associated species recorded in Colombia, this key could be useful for identifying scale insects associated with coffee in other tropical regions, extending also to species collected from the aerial parts of the hosts.

    Author contributions

    The authors confirm contributions to the paper as follows: study conception and design: Caballero A, Kondo T; data collection: Caballero A, Kondo T; analysis and interpretation of results: Caballero A, Kondo T; draft manuscript preparation: Caballero A, Kondo T. Both authors reviewed the results and approved the final version of the manuscript.

    Data availability

    The data (microscopy slides of specimens) that support the findings of this study are available in the Scale insect repository of the entomological museum Universidad Nacional Agronomia Bogota – UNAB, Facultad de Ciencias Agrarias, Colombia. All data generated or analyzed during this study are included in this published article and its supplementary information files.

    Acknowledgments

    The authors thank Dr. Andrea Ramos-Portilla for clarifying some aspects of the morphological variations of Rhizoecus species and Dr. Penny Gullan (Australian National University, Canberra, Australia) for reviewing an earlier version of the manuscript. Many thanks to Erika Valentina Vergara (AGROSAVIA) and Dr. Francisco Serna (Universidad Nacional de Colombia) for their help to access the Museum UNAB. Special thanks to Dr Giuseppina Pellizzari (University of Padova, Italy) for advice on scientific nomenclature. This study was financed by Colciencias (Programa Nacional de Ciencias Básicas [National Program on Basic Sciences]), code 110165843233, contract FP44842-004-2015), by the entomological museum UNAB (Facultad Ciencias Agrarias, Universidad Nacional de Colombia, sede Bogotá) and by Federación Nacional de Cafeteros.

  • The authors declare that they have no conflict of interest.

  • [1]

    Li J, Stoliarov SI. 2013. Measurement of kinetics and thermodynamics of the thermal degradation for non-charring polymers. Combustion and Flame 160(7):1287−97

    doi: 10.1016/j.combustflame.2013.02.012

    CrossRef   Google Scholar

    [2]

    Fang J, Tu R, Guan JF, Wang JJ, Zhang YM. 2011. Influence of low air pressure on combustion characteristics and flame pulsation frequency of pool fires. Fuel 90(8):2760−66

    doi: 10.1016/j.fuel.2011.03.035

    CrossRef   Google Scholar

    [3]

    Xia Y. 2016. Henan Pingdingshan "5·25" particularly serious fire accident. Production safety in China 11(4):48−49

    Google Scholar

    [4]

    Ozlem S, Aslan-Gürel E, Rossi RM, Hacaloglu J. 2013. Thermal degradation of poly(isobornyl acrylate) and its copolymer with poly(methyl methacrylate) via pyrolysis mass spectrometry. Journal of Analytical and Applied Pyrolysis 100:17−25

    doi: 10.1016/j.jaap.2012.10.024

    CrossRef   Google Scholar

    [5]

    CABR. 2012. Technical Guidelines for External Insulation and Fire Isolation Belts for Building Exterior Walls. www.mohurd.gov.cn/gongkai/zhengce/zhengcefilelib/201212/20121206_224429.html#:~:text
    [6]

    Tsai KC. 2011. Influence of sidewalls on width effects of upward flame spread. Fire Safety Journal 46(5):294−304

    doi: 10.1016/j.firesaf.2011.03.006

    CrossRef   Google Scholar

    [7]

    Tsai KC. 2009. Width effect on upward flame spread. Fire Safety Journal 44(7):962−67

    doi: 10.1016/j.firesaf.2009.06.003

    CrossRef   Google Scholar

    [8]

    Jiang L, He JJ, Sun JH. 2018. Sample width and thickness effects on upward flame spread over PMMA surface. Journal of Hazardous Materials 342:114−20

    doi: 10.1016/j.jhazmat.2017.08.022

    CrossRef   Google Scholar

    [9]

    Jiang L, Miller CH, Gollner MJ, Sun JH. 2017. Sample width and thickness effects on horizontal flame spread over a thin PMMA surface. Proceedings of the Combustion Institute 36(2):2987−94

    doi: 10.1016/j.proci.2016.06.157

    CrossRef   Google Scholar

    [10]

    Jiang L, Xiao H, An W, Zhou Y, Sun J. 2014. Correlation study between flammability and the width of organic thermal insulation materials for building exterior walls. Energy and Buildings 82:243−49

    doi: 10.1016/j.enbuild.2014.06.013

    CrossRef   Google Scholar

    [11]

    Rangwala AS, Buckley SG, Torero JL. 2007. Upward flame spread on a vertically oriented fuel surface: The effect of finite width. Proceedings of the Combustion Institute 31(2):2607−15

    doi: 10.1016/j.proci.2006.07.235

    CrossRef   Google Scholar

    [12]

    Gollner MJ, Xie Y, Lee M, Nakamura Y, Rangwala A. 2012. Burning behavior of vertical matchstick arrays. Combustion Science and Technology 184:585−607

    doi: 10.1080/00102202.2011.652787

    CrossRef   Google Scholar

    [13]

    Leventon IT, Stoliarov SI. 2013. Evolution of flame to surface heat flux during upward flame spread on poly(methyl methacrylate). Proceedings of the Combustion Institute 34(2):2523−30

    doi: 10.1016/j.proci.2012.06.051

    CrossRef   Google Scholar

    [14]

    Emmons HW. 1956. The film combustion of liquid fuel. Journal of Applied Mathematics and Mechanics 36(1-2):60−71

    doi: 10.1002/zamm.19560360105

    CrossRef   Google Scholar

    [15]

    Liu X, Zhu GQ, Chu TW, Zhang XJ. 2022. Effect of fuel coverage on vertical fire spread of discontinuous solid. Fire Science and Technology 41(2):201−205

    Google Scholar

    [16]

    Cai ML. 2021. Effect of material inclination angle and concave vertical channel on discontinuous fire propagation and its mechanism. Thesis. China University of Mining and Technology, Jiangsu, China.
    [17]

    Williams FA. 1985. Combustion theory. 2nd Edition. Boca Raton: CRC Press. https://doi.org/10.1201/9780429494055
    [18]

    An W, Huang X, Wang Q, Zhang Y, Sun J, et al. 2015. Effects of sample width and inclined angle on flame spread across expanded polystyrene surface in plateau and plain environments. Journal of Thermoplastic Composite Materials 28(1):111−27

    doi: 10.1177/0892705713486132

    CrossRef   Google Scholar

    [19]

    Zhang Y. 2012. Study on flame spread characteristics of typical carbonizable solid materials. Thesis. University of Science and Technology of China, Anhui, China.
    [20]

    Incropera FP, Dewitt DP, Bergman TL, Lavine AS. 1985. Fundamentals of heat and mass transfer. 2nd Edition. Hoboken, NJ: John Wiley & Sons. pp. 939−40.
    [21]

    Hu L, Tang F, Wang Q, Qiu Z. 2013. Burning characteristics of conduction-controlled rectangular hydrocarbon pool fires in a reduced pressure atmosphere at high altitude in Tibet. Fuel 111:298−304

    doi: 10.1016/j.fuel.2013.04.032

    CrossRef   Google Scholar

    [22]

    Luo S, Xie Q, Tang X, Qiu R, Yang Y. 2017. A quantitative model and the experimental evaluation of the liquid fuel layer for the downward flame spread of XPS foam. Journal of Hazardous Materials 329:30−37

    doi: 10.1016/j.jhazmat.2017.01.028

    CrossRef   Google Scholar

    [23]

    Zhao LY. 2019. Effects of gas convection and sample width on typical solid ignition and downwind fire propagation. Thesis. University of Science and Technology of China, Anhui, China.
    [24]

    Pizzo Y, Consalvi JL, Querre P, Coutin M, Porterie B. 2009. Width effects on the early stage of upward flame spread over PMMA slabs: Experimental observations. Fire Safety Journal 44(3):407−14

    doi: 10.1016/j.firesaf.2008.09.003

    CrossRef   Google Scholar

  • Cite this article

    Wu Z, Zhu G, Peng M, Chen F, Chai G, et al. 2024. Experimental study on the influence of material width on discrete fire spread in open space. Emergency Management Science and Technology 4: e014 doi: 10.48130/emst-0024-0014
    Wu Z, Zhu G, Peng M, Chen F, Chai G, et al. 2024. Experimental study on the influence of material width on discrete fire spread in open space. Emergency Management Science and Technology 4: e014 doi: 10.48130/emst-0024-0014
    shu

Figures(15)  /  Tables(3)

Download PDF

Article Metrics

Article views(2239) PDF downloads(375)

Other Articles By Authors

ARTICLE   Open Access    

Experimental study on the influence of material width on discrete fire spread in open space

  • 1.

    School of Safety Engineering, China University of Mining and Technology, Xuzhou 221116, China

  • 2.

    Yunlong Lake Deep Earth Science and Engineering Laboratory , Xuzhou 221116, China

  • 3.

    School of Safety Engineering, Changzhou University, Changzhou 213164, China

  • Received: 12 March 2024
  • Revised: 03 May 2024
  • Accepted: 22 May 2024
  • Published online: 08 July 2024
Emergency Management Science and Technology  4,  Article number: e014  (2024)  |  Cite this article

Abstract: This study addresses the significant fire hazards associated with using thermoplastic materials, particularly PMMA (poly methyl methacrylate), which are prone to flammability and high calorific values. By employing a methodology that combines small-scale experiments and theoretical analysis, this paper investigates the impact of material width on the behavior of discrete flames in open spaces, using specimens ranging from 5 to 10 cm in width. The findings indicate that an increase in specimen width positively affects the burning area and brightness, while the dimensionless flame height and heat release rate per unit width exhibit a negative power law decay with increasing width. This suggests that beyond a critical width, further increases in width have little influence on flame propagation. The results of this study contribute to a better understanding of fire dynamics in thermoplastics and provide valuable insights that could lead to enhanced fire safety standards and material designs. The originality of this research lies in its detailed analysis of how material dimensions influence flame behavior, a topic that has not been extensively explored before, offering significant practical value in applications where fire safety is crucial.

    HTML

    Introduction

    • Thermoplastic materials are characterized by light weight, easy processing, good thermal insulation performance, low price, etc., and are widely used in building exterior wall insulation materials, pipes, and floor curtain wall decoration materials. Among them, PMMA (Poly methyl methacrylate), a common thermoplastic with good transparency, optical properties, weather resistance, chemical resistance and hardness is widely used in daily life and high-tech industries[1]. The wide range of applications and good prospects of thermoplastic materials have led researchers around the world to invest great efforts in related research fields, but the lower glass transition temperature, pyrolysis temperature, and oxygen index, the larger calorific value of combustion and smoke production and other characteristics make the material a greater flame hazard. For example, the color steel plate with a core filled with thermoplastic insulation material is widely used in temporary rooms at construction sites for building projects because of its light weight, high strength, good heat preservation, and convenient installation. However, several flames have occurred in recent years due to combustible thermoplastics wrapped inside its steel plate sandwich.[2] In Henan, Lushan County (China) on May 2015, a particularly significant flame accident occurred, Kang Leyuan's elderly apartment room inside an electrical wiring failure, the flame quickly in the polystyrene material filled with color steel plate sandwich spread, resulting in a total of 39 deaths, six people were injured, as well as more than 20 million yuan of direct economic losses[3].

      PMMA is a flame combustion field that commonly uses thermoplastic polymers. It has advantages of good combustion performance, complete combustion, low ignition temperature, slow burning speed, low carbonization, and good reproducibility[4], and its combustion and flame spread characteristics can represent real flame scenes. Shanghai's 'Technical Guidelines for Flame Barrier for External Wall Insulation of Buildings' stipulates[5] that the horizontal flame barrier for external wall insulation of buildings should not be less than 300 mm in height, and the vertical flame barrier should not be less than 200 mm wide, but the maximum width of the material in the specific construction has not been stipulated. In the actual flame scenario, the width of the material is an important factor affecting the spread of solid surface flame.

      Tsai[6,7] and Jiang et al.[8−10] investigated the effect of specimen width on the spread of unilateral downstream flame, and the results showed that when the specimen width is less than the critical width, the rate of downstream flame spread increases with the increase of width, and when the specimen width is greater than the critical width, the effect of width effect on the spread of downstream flame is not obvious. For narrower specimens, the reduction of pyrolysis near the edge of the specimen is more obvious. Rangwala et al.[11] investigated the width effect in vertical downstream flame propagation and found that in laminar flame, the diffusion loss effect of pyrolysis gases to the two sides increases gradually with the increase of the width of the material and established a theoretical model. Gollner et al.[12] investigated the behavioral patterns of corrugated paper in the early stage of vertical downstream flame propagation and found that the pyrolysis front loss effect is gradually enhanced with the increase of the width of the material. Leventon et al.[13] measured the thermal feedback of PMMA samples of different heights in the process of vertical flame spreading, and found that the total heat flow of the bottom of the fuel was much larger than that of the upper part due to the laminar flame at the bottom position of the flame spreading stationary distance being much smaller. Jiang et al.[8] carried out experiments in vertical downstream flame spreading on PMMA and investigated the sample width effect and developed a global mass loss rate prediction model with coupled fuel width based on Emmons' assumption[14].

      From the above studies, it can be seen that the current research on the width effect on flame-spreading behavior mostly focuses on the study of downstream continuous flame spreading, while in fact in real life, most of the materials are in a non-continuous state and there is no definitive conclusion on the effect of width on flame spreading. Combined with a previous study[15], in the discrete flame spread rate research process with combustible material coverage of 62.55%, the flame height and mass loss rate have reached the peak of the conclusion, this paper selects the discrete state of the solid size of a height of 6 cm and 4 cm of air spacing length, the conditions of the fuel coverage of 60%, can maximize the acceleration of flame propagation. By selecting discrete PMMA sizes with different widths, how the flame growth phase and flame stabilization phase of discrete flame propagation are affected by the width of the material in open space is analyzed.

      This paper aims to investigate the characteristics of flame spread on the surface of PMMA under varying widths, providing an in-depth analysis of the influence of material width on the mechanism of flame spread on discretely distributed solid surfaces. This not only advances the fundamental research on the evolution of fire behavior in discrete solid distributions but also offers significant guidance for fire prevention design and firefighting strategies in scenarios such as building exterior insulation fires.

    Experiments

    • Investigating the vertical flame spread process of discrete polymethyl methacrylate (PMMA) involved a series of experiments conducted under controlled indoor conditions, including ambient temperature and the absence of wind. The objective was to explore the influence of confined space on flame spread characteristics across different widths. This study focused on comprehending the flame spread mechanism through close observation, documentation of experimental phenomena, and analyzing flame parameters during growth and stabilization.

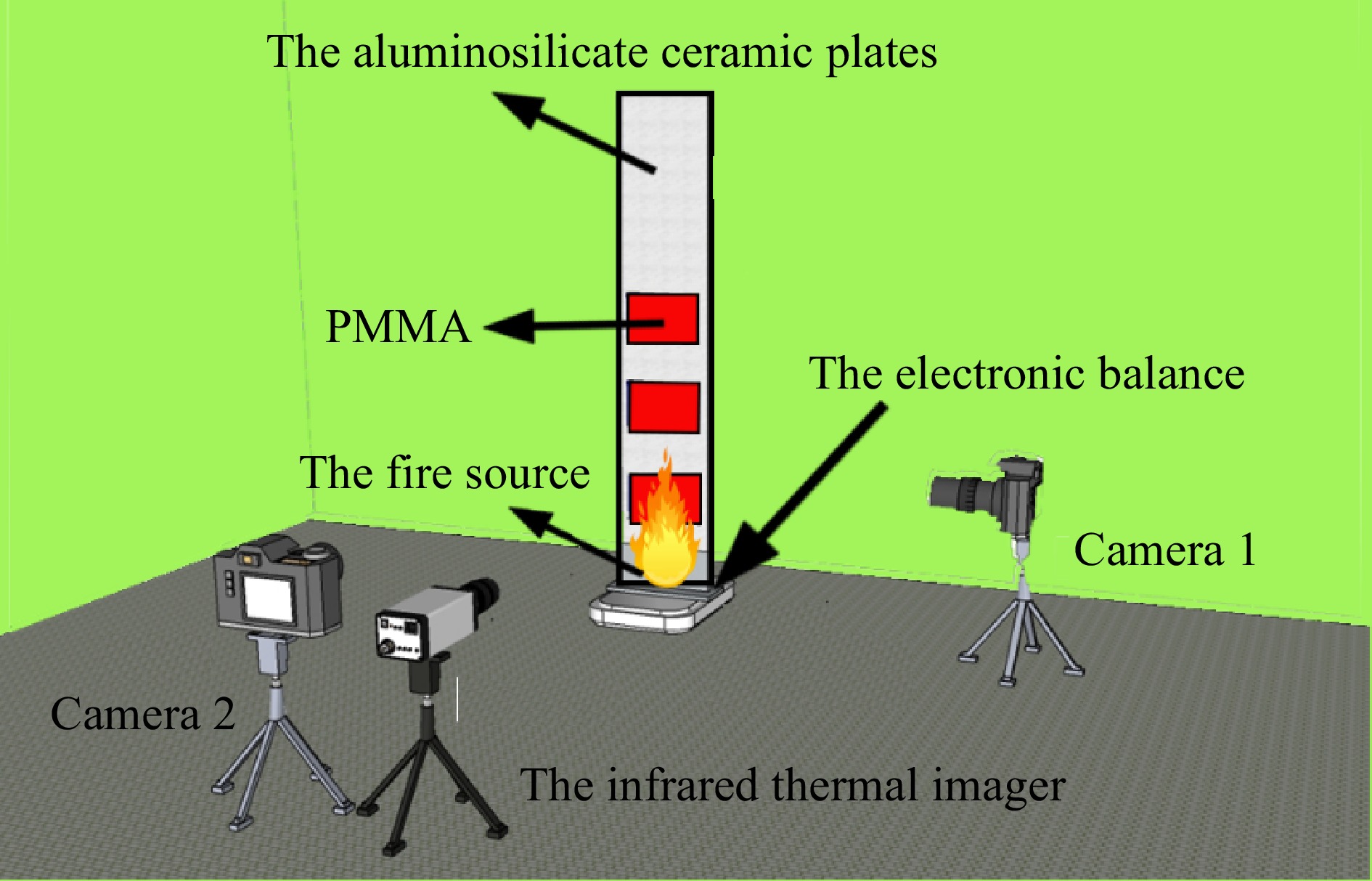
      A comprehensive experimental system, depicted in Fig. 1, comprised a specimen fixation device and a data acquisition device. A green fireproof cloth served as a background curtain to enhance flame morphology clarity and ensure experimental safety. The camera used was the XT-3 model, featuring a magnification of 0.75 times, a display delay of 0.005 s, and a refresh rate of approximately 100 frames per second (fps). Flame characteristics were assessed by decomposing the video footage into frame-by-frame grayscale images, and the brightness value of each pixel was calculated using Matlab. A suitable grayscale threshold was set to distinguish between flame and non-flame areas.

      Figure 1. 

      Experimental apparatus.

      In the experiment, the PMMA sample was positioned above the base and ignited using a DREMEL 2200-4 multi-function gas burner, which initiated spontaneous combustion of the PMMA array. To mitigate the influence of heat from the igniter on the fuel array, a fire-retardant board measuring 30 cm long, 10 cm wide, and 2 cm thick was employed as a baffle. This setup effectively blocked the upward transfer of external heat during the ignition process, ensuring that the observed effects were solely attributable to the material properties of the PMMA.

      The mass sensor utilized was the ES-30001TS model, capable of measuring up to 30 kg with a precision of 0.1 g. The thermal imager employed was the MAG30 model, operating within a measurement wavelength range of 7.5 to 14 μm, featuring a pixel size of 17 μm. The acquisition frame rate was set at 50 Hz, while the output frame rate was maintained at 25 Hz.

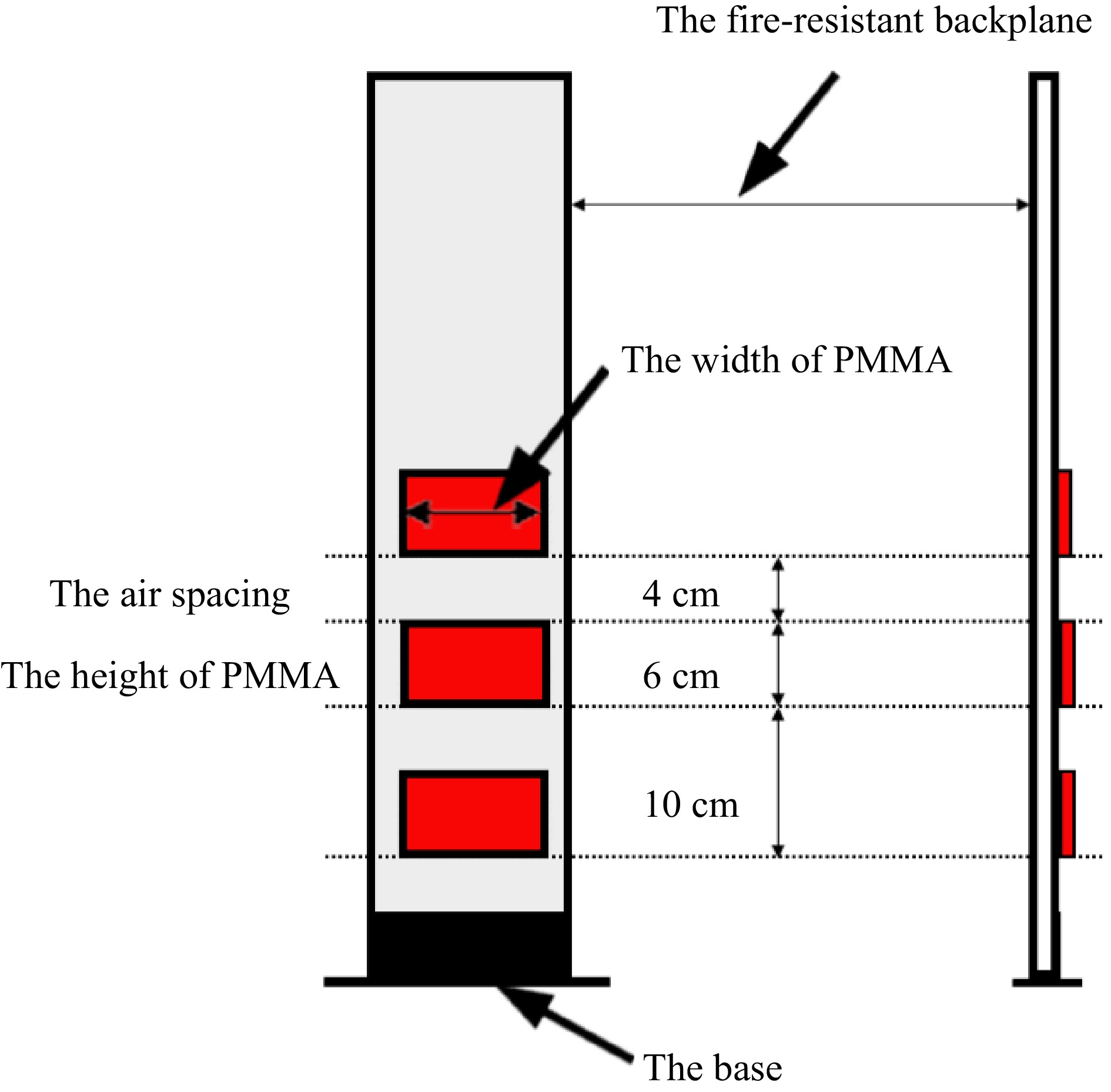
      This paper employs a vertical flame spread system to simulate the flame propagation process on a discretely distributed solid surface, as illustrated in Fig. 2. The system consists of a base and a fire-resistant backplane. The base securely positions the fire backing plate perpendicular to the ground, while the fire-resistant backplane accommodates discrete material blocks made of aluminosilicate ceramic plates known for their low thermal conductivity, high stability, and corrosion resistance. The dimensions of the fire-resistant backplane used in this study are 50 cm × 15 cm × 2 cm.

      Figure 2. 

      Experimental device for PMMA.

      In this study, a discrete PMMA block measuring 6 cm in height, with an air spacing of 4 cm and a thickness of 1 cm, was selected as the specimen to examine the effects of different specimen widths and restricted distances. Furthermore, considering the thermal penetration thickness of PMMA is only 0.2 cm, while the specimen thickness employed in this study is 1 cm, the material can be regarded as thermally thick. Lastly, a silicone-free high-temperature sealant was used to affix the PMMA block onto the fire-resistant backplane, composed of a polymer material exhibiting excellent elasticity, adhesion, sealing properties, as well as remarkable resistance to high temperatures, making it suitable for long-term use below 800 °C and fire resistance up to 1,280 °C.

      PMMA single sample height and air spacing distance are fixed, respectively, 6 cm and 4 cm, the width of the specimen is selected as a range of 5−10 cm, and a total of 18 conditions are designed, as shown in Table 1, to facilitate experimental comparisons, the specimen in a single piece, two pieces, and three pieces, respectively, correspond to the letters A, B, and C. For the sake of experimental comparison, the single block, two blocks and three blocks in the specimen correspond to the letters A, B and C, respectively, and the numbers behind the letters represent the corresponding widths of conditions (cm). To ensure the repeatability and validity of the experiment, at least three experiments were repeated under each condition.

      Table 1.  Table of conditions for discrete solids of different widths.

      Width (cm) 5 6 7 8 9 10
      Single piece of PMMA A-5 A-6 A-7 A-8 A-9 A-10
      Two pieces of PMMA B-5 B-6 B-7 B-8 B-9 B-10
      Three pieces of PMMA C-5 C-6 C-7 C-8 C-9 C-10
    Results and discussion

      Analysis of the influence of width on discrete flame morphology

    • Flame morphology is a visual parameter that reflects the flame propagation process. In this section, discrete flame propagation characteristics and the effect of material width on flame morphology in open spaces will be analyzed based on frontal and lateral flame morphology diagrams.

      Width affects flame morphology

    • A schematic diagram of the stable combustion stage of a single PMMA sheet under different width conditions is shown in Fig. 3. As can be seen from the figure, with the increase in the width of the material, the flame-burning area increases, and the flame width also increases. In comparative analysis, the latter three diagrams consistently demonstrate markedly greater flame brightness than the initial trio. This observation is primarily attributable to the wider widths of the specimens tested, which increase the combustion area. As a result, there is a corresponding uptick in the release of flammable gases, intensifying the combustion process. Consequently, flames from broader specimens exhibit a heightened luminosity relative to those from narrower counterparts.

      Figure 3. 

      Schematic diagram of the front side of a single piece of PMMA burning with different widths.

      Figure 4 shows the front view of the stabilized combustion stage of two PMMA plates under different widths. It can be seen that under different fuel widths, the discrete fuels all present roughly the same flame morphology during the stable combustion process: the flame presents stable laminar combustion on the surface of the first PMMA plate; turbulent combustion on the surface of the second PMMA plate, and the flame presents a more violent pulsation phenomenon and intermittent phenomenon above the material, which is due to the flame body of the second PMMA is subject to the first PMMA plate burning flame body's buoyancy drive and flame superposition, resulting in the flame body shaking violently.

      Figure 4. 

      Schematic diagram of the burning front side of two pieces of PMMA with different widths.

      At the same time, in the frontal schematic, the flames in the material air spacing all present a concave tendency from both sides to the middle, which is because the flame front presents an inverted V tendency in the process of the flame burning uniformly, which is the same flame morphology as that presented by the flame front above the second piece. That is to say, the discrete flame spreads are roughly the same in longitudinal morphology and the differences are in the transverse flame width and flame brightness, the wider the width, the greater the flame brightness.

      Figure 5 shows the front view of the stable combustion of three PMMA plates under different widths. It can be seen that the three PMMA plate's combustion presents the same law with single and two PMMA plates, i.e., the flame width increases with the increase of the fuel width, and the flame tends to converge from the two sides to the center at the air spacing, which is consistent with the inverted V shape presented by the flame front. Meanwhile, it is the same as the schematic diagram of the front of the two PMMA panels, i.e., the first PMMA panel presents a stable laminar flow combustion state, while the first and second PMMA panels are affected by the bottom flame buoyancy drive and the flames present obvious jittering and intermittent phenomena.

      Figure 5. 

      Schematic diagram of the burning front side of three PMMA plates with different widths.

      Comprehensive analysis

    • According to the above flame pattern, when the flame spreads on the discrete distribution solid surface, the flame shows stable laminar combustion in the A layer, and B and C layers are subjected to violent flame jitter and intermittent phenomenon at the bottom and show the tendency to concave from both sides to the middle in the frontal air spacing, and the flame peak shows obvious inverted V phenomenon as shown in the frontal schematic diagram. The flame shows the tendency to concave inward in the air spacing and shows wall-to-wall phenomena in the air spacing and the upper part of the wall.

      The flame shows a tendency of inward concavity at the air interval and wall sticking phenomenon at the air interval and the upper part of the wall, while the flame thickness at the effective solid surface shows a tendency to increase from the bottom to the upper part of the flame, as shown in the side schematic diagrams. Under different widths, the flame pattern in the discrete distribution of the solid surface shows the same pattern, but the flame pattern in the direction of the width of the difference is more obvious, the strongest contrast is the 5 and 10 cm width of the conditions, the larger the width, the more fully pyrolyzed the material, the flame brightness is brighter. At the same time, the flame in different conditions shows the thickness in the center line is larger than the two sides of the characteristics, this is because part of the combustion vapors to the material on both sides of the diffusion of the flame width is greater than the width of the sample, and the phenomenon from the center line to the two sides of the decreasing step by step.

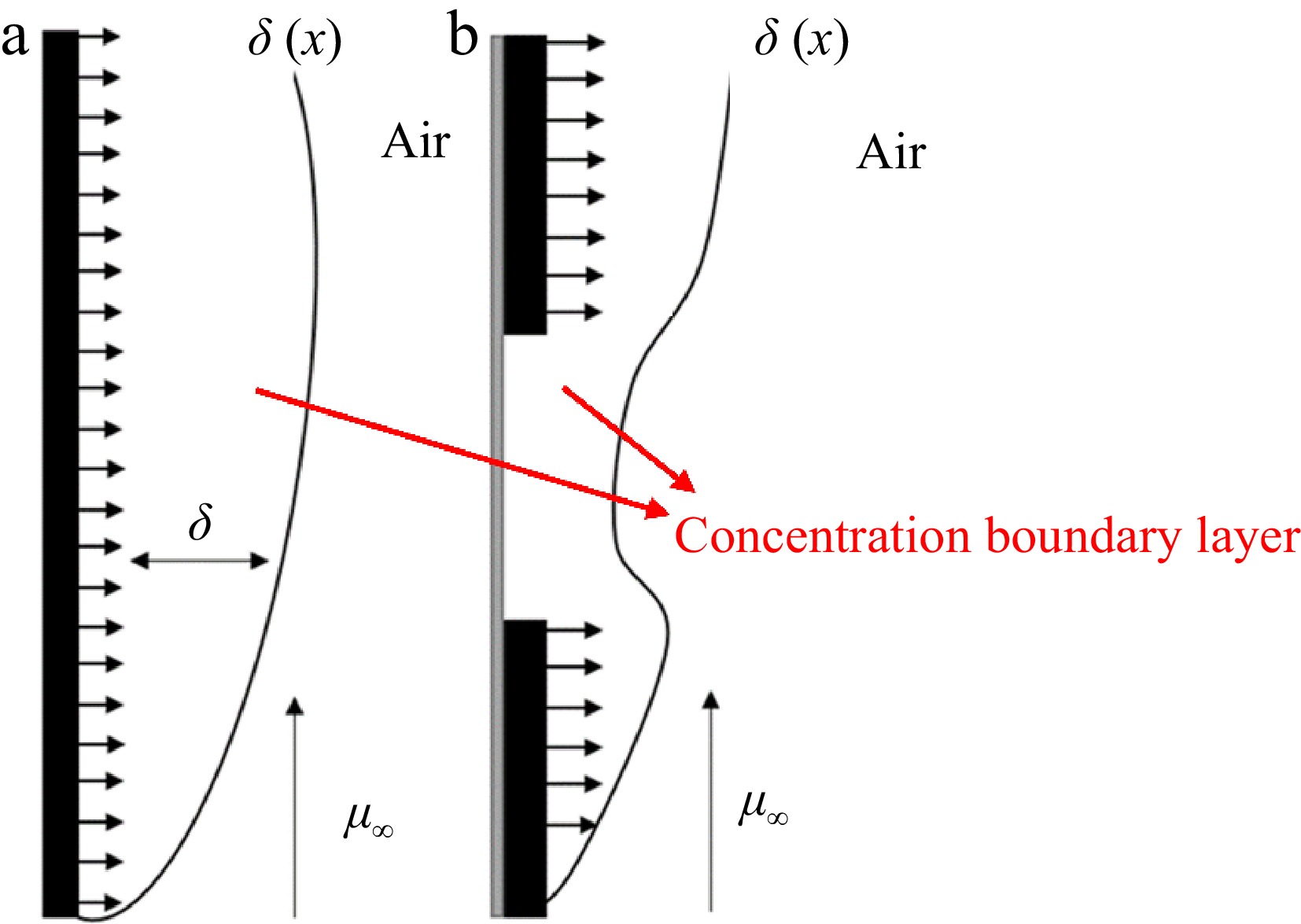
      For a solid that is burning, to effectively explain the heat and mass transfer process between the solid and the airflow flowing over the solid surface, according to the flame spreading pattern process, Cai[16] established the concept of the boundary layer on the surface of solid materials to divide the boundary layer into three layers: velocity boundary layer, thermal boundary layer, and concentration boundary layer.

      Figure 6 shows a schematic diagram of the continuous and discrete concentration boundary layer. As can be seen from the figure: for continuous solids, the thermal decomposition of solids to generate combustible gases driven by buoyancy to form a concentration boundary layer, with continuous development of the pyrolysis front, the thickness of the concentration boundary layer is also gradually increased in the formation of a concentration gradient on the surface of solids in the fluid region; for discrete solids, the concentration boundary layer in the air interval at the inward trend of depression, which is due to the absence of pyrolysis gases generated at the air interval, and this is because no pyrolysis gas is generated at the air gap, and the pyrolysis gas generated by the combustion of the lower material plate is entrained by the air at the gap, resulting in the phenomenon that the overall concentration thickness decreases.

      Figure 6. 

      Concentration boundary layer (a) continuous, and (b) discontinuous.

      Analysis of the influence of width on the stability stage of discrete flame spread

    • In this section, experimental samples of different widths are set up and the parameters of flame height, mass loss rate, and heat release rate are analyzed. By processing and fitting the experimental data, the relationship between the parameters in the stabilization stage with width is derived.

      Flame height

    • The study of the flame height in the stable stage is of great significance to the discrete flame-spreading behavior. Since the solid material shows turbulence after complete combustion in the experimental process, the fluctuation is large, so this paper selects the average value of the flame height of the stable combustion stage of the material as the flame height in this experiment.

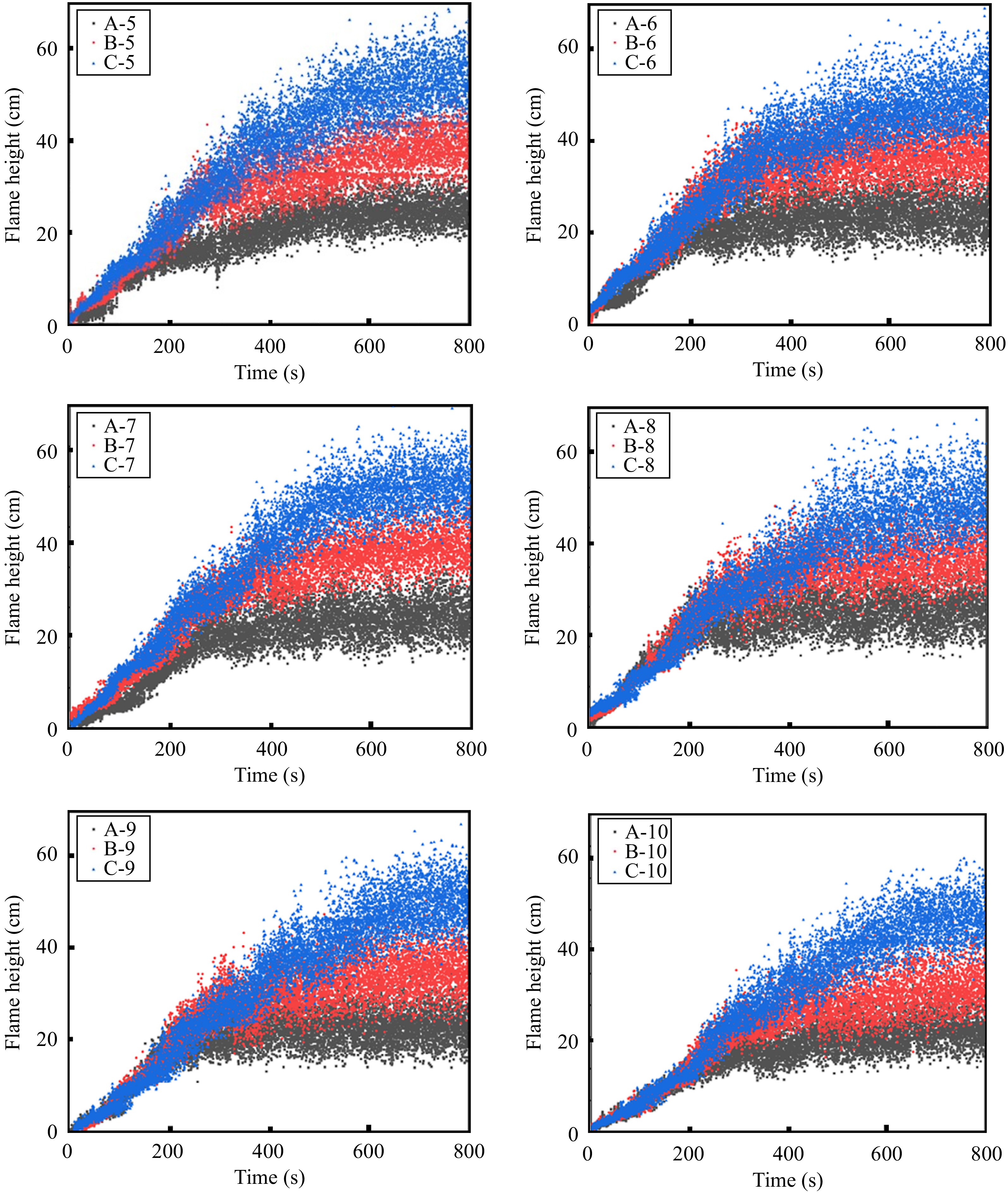
      Figure 7 shows a schematic diagram of the flame height under different working conditions. As can be seen from the figure, in the initial stage of combustion of the material, the flame height is small, and the flame moves up and down more gently, with the continued development of the flame, the flame burns sufficiently, the flame height shows a stabilizing trend, the flame height fluctuates up and down within the average value, which tends to stabilize the situation. This is mainly because: in the initial stage of combustion, due to the flame pyrolysis area being small, the PMMA plate pyrolysis gas release is small, the combustion is not sufficient, so the flame height is small; with the rise of the flame top, the unburned area of more material being heated causes the release of flammable gases, when the material is uniformly burned, pyrolysis release of gases tends to stabilize the rate of loss of quality of the material stabilized at this time and the flame height change tends to stabilize.

      Figure 7. 

      Schematic diagram of flame height at the steady stage.

      From Fig. 7, the average height of the flame, and the average height of conditions A-5, A-6, A-7, A-8, A-9, and A-10 are 25.46, 25.60, 27.24, 29.31, 30.63, and 32.85 cm, respectively. From the section on flame morphology, the first layer of the PMMA plate combustion at the bottom of the combustion presents laminar combustion and combustion stability, in the upper part of the flame due to the bottom flame buoyancy dominated by a turbulent state. Combustion is stable, in the upper part of the flame due to the bottom flame buoyancy dominated by the turbulence state, it is known from the flame height that the width effects in the combustion of the first PMMA plate is more obvious, i.e., the larger the width, the higher the flame height. The flame heights of conditions B-5, B-6, B-7, B-8, B-9, and B-10 are 40.17, 42.26, 43.81, 45.19, 46.73, and 47.18 cm, and from the data, it can be seen that the larger the width, the higher the flame height, and the difference between the flame heights of the conditions with 5 and 10 cm widths is further increased by the presence of the air spacing. further becomes larger. This means that the effect of the presence of air spacing on the width is more pronounced. The flame heights for conditions C-5, C-6, C-7, C-8, C-9 and C-10 are 54.83, 56.18, 59.83, 63.17, 65.86, and 68.86 cm. This further proves that the presence of an air spacer further increases the width effect. Combined with the change of pyrolysis front position and flame spreading speed in the previous section, it can be seen that although the speed of the 6 cm width flame will be reduced during the spreading process, the height of the flame stabilization stage will be greater than that of the 5 cm width specimen when the material is fully burned. Therefore, the larger the width, the higher the flame height in the stabilization stage.

      The average flame height during the stabilization phase was plotted as shown in Fig. 8.

      Figure 8. 

      The relationship between average flame height and width.

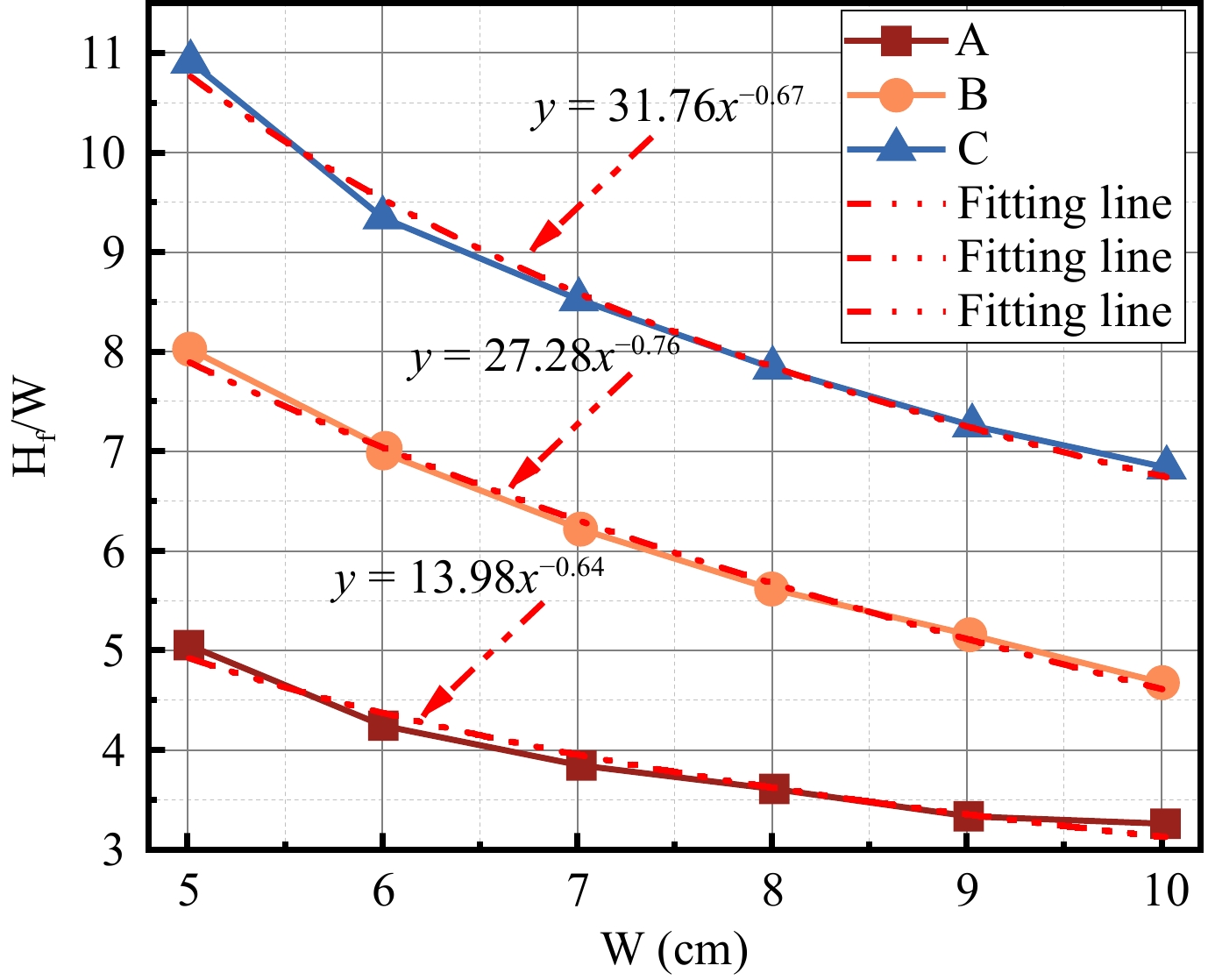
      Dimensionless flame height is the ratio of the average flame height to the width of the material (H/W)[17]. In the width effect, the dimensionless flame height decreases with increasing specimen width. The diffusion flame height is mainly determined by the buoyancy and inertia forces, and a dimensionless number, the Froude number is usually introduced to describe the magnitude relationship between the buoyancy and inertia forces, defining the Froude number as: Fr=u20/Wg . When the Fr number is small, the flame height is controlled by the buoyancy force, and the dimensionless flame height satisfies Hf/W Frn. Therefore, the dimensionless flame height and width have the following relationship[17]:

      Hf/W∼W−n (1)

      An et al.[18] obtained 0.7 < n < 0.9; Zhang et al.[19] obtained 1/5 < n < 1/3. After converting the above obtained average flame height to dimensionless flame height, the relationship between the width and dimensionless flame height is plotted in Fig. 9, and the image is fitted by applying Eqn (1). It can be seen that the dimensionless flame height is well fitted to the width of the specimen, and with the increase of the width, the dimensionless flame height shows the tendency to decay as a negative power law, which is shown from the figure that the value of n ranges from 0.6 to 0.8. In general, the width effect still exists with the increase in the number of discrete blocks, and the more the number of blocks is, the more obvious the tendency to decrease is 0.6~0.8. In general, with the increase of the number of discrete blocks, the width effect still exists, and the more the number of blocks, the more obvious the trend of decreasing dimensionless flame height.

      Figure 9. 

      The relationship between dimensionless flame height and sample width.

      Rate of mass loss

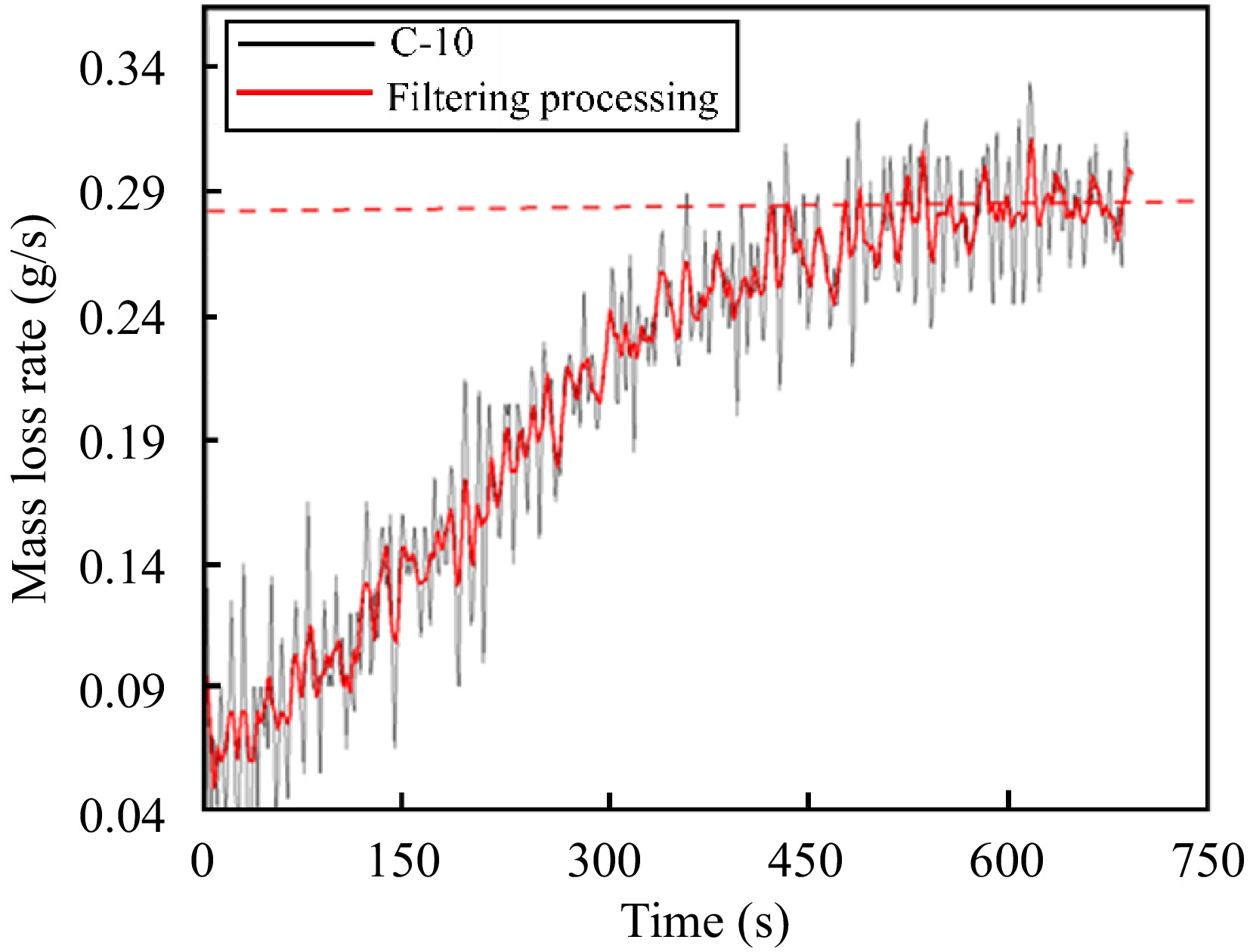
    • The material mass loss rate in the stabilization stage can be obtained by the first-order derivation of the mass loss curve. However, in the experimental process, the data acquisition time of the computer is smaller than the response time of the mass sensor, which leads to large noise interference in the process of deriving the mass loss curve, so it is necessary to filter the mass loss rate curve to get a smoother curve. Take the C-10 condition as an example, draw the mass loss rate processing diagram, as shown in Fig. 10, and do the mean value processing for the mass loss rate in the stabilization stage to get the average mass loss rate at the stabilization moment is 0.286 g/s.

      Figure 10. 

      C-10 Mass loss rate processing diagram.

      Equivalent treatment as described above for the other conditions yields the instantaneous mass loss rate at the moment of the stabilization phase as shown in Table 2.

      Table 2.  Rate of material mass loss (g/s).

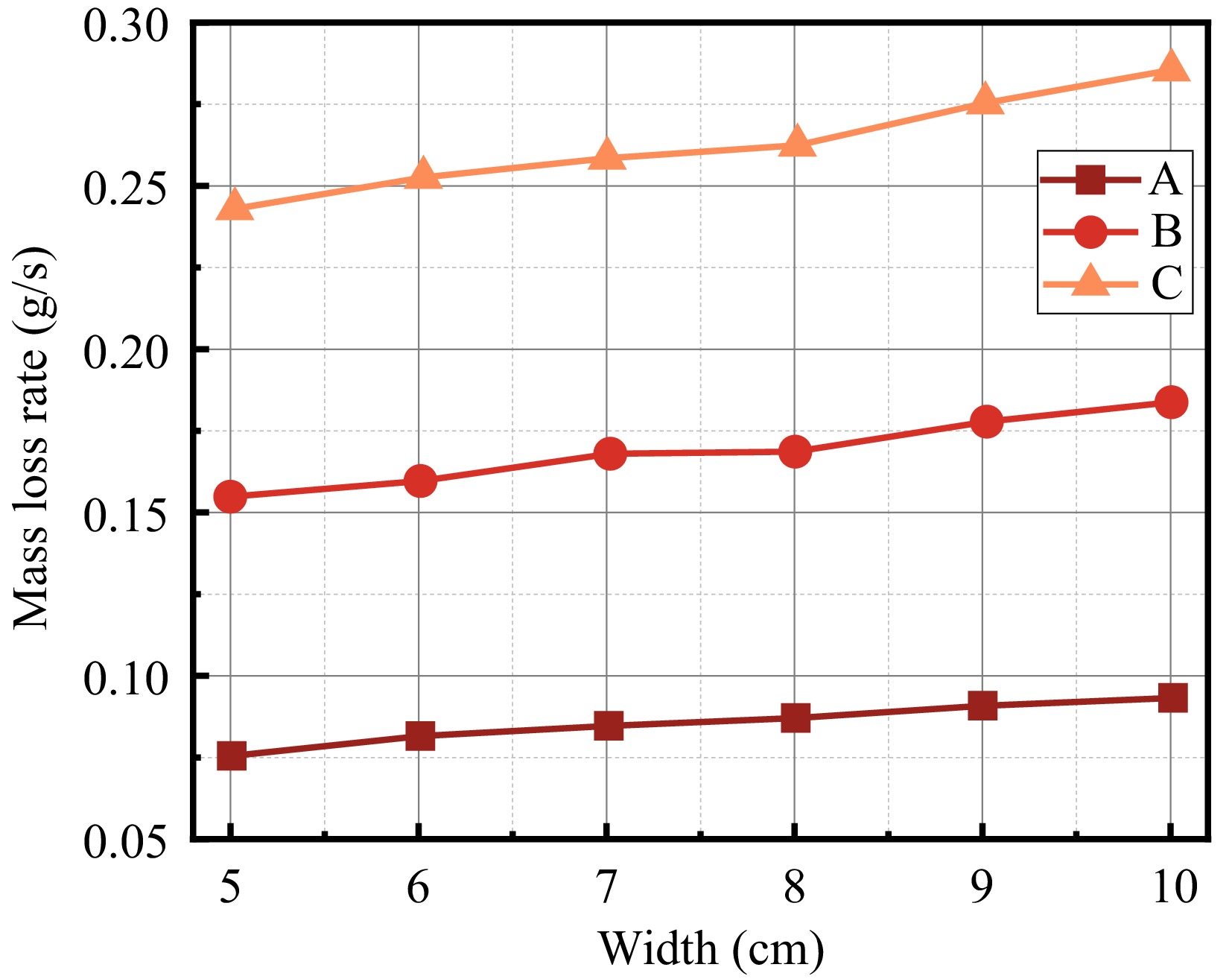
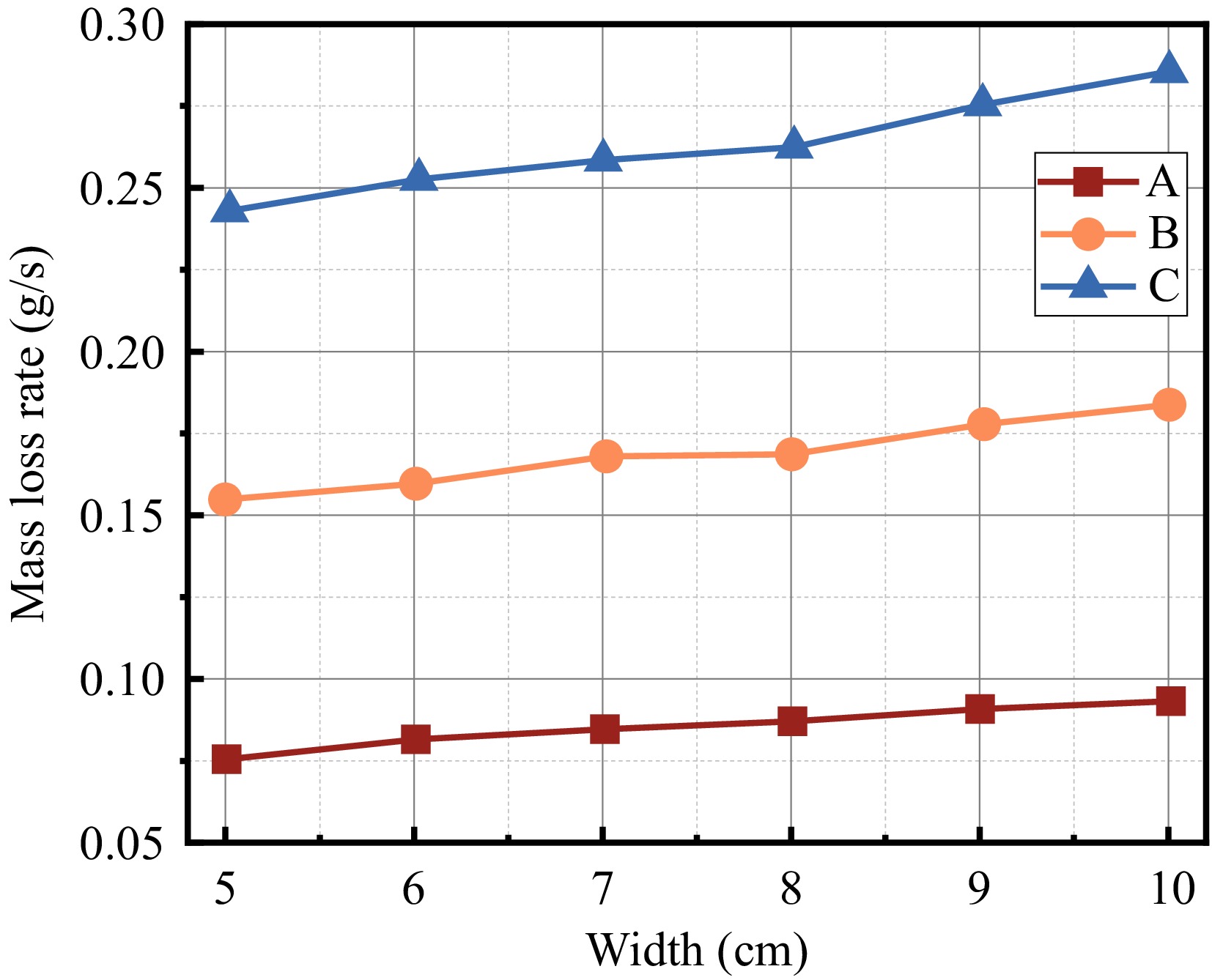
      Conditions Height
      5 6 7 8 9 10
      A 0.076 0.082 0.085 0.087 0.091 0.093
      B 0.155 0.160 0.169 0.170 0.179 0.184
      C 0.243 0.253 0.260 0.263 0.276 0.286

      Table 3.  Physical parameters of PMMA in Eqn (2)[8].

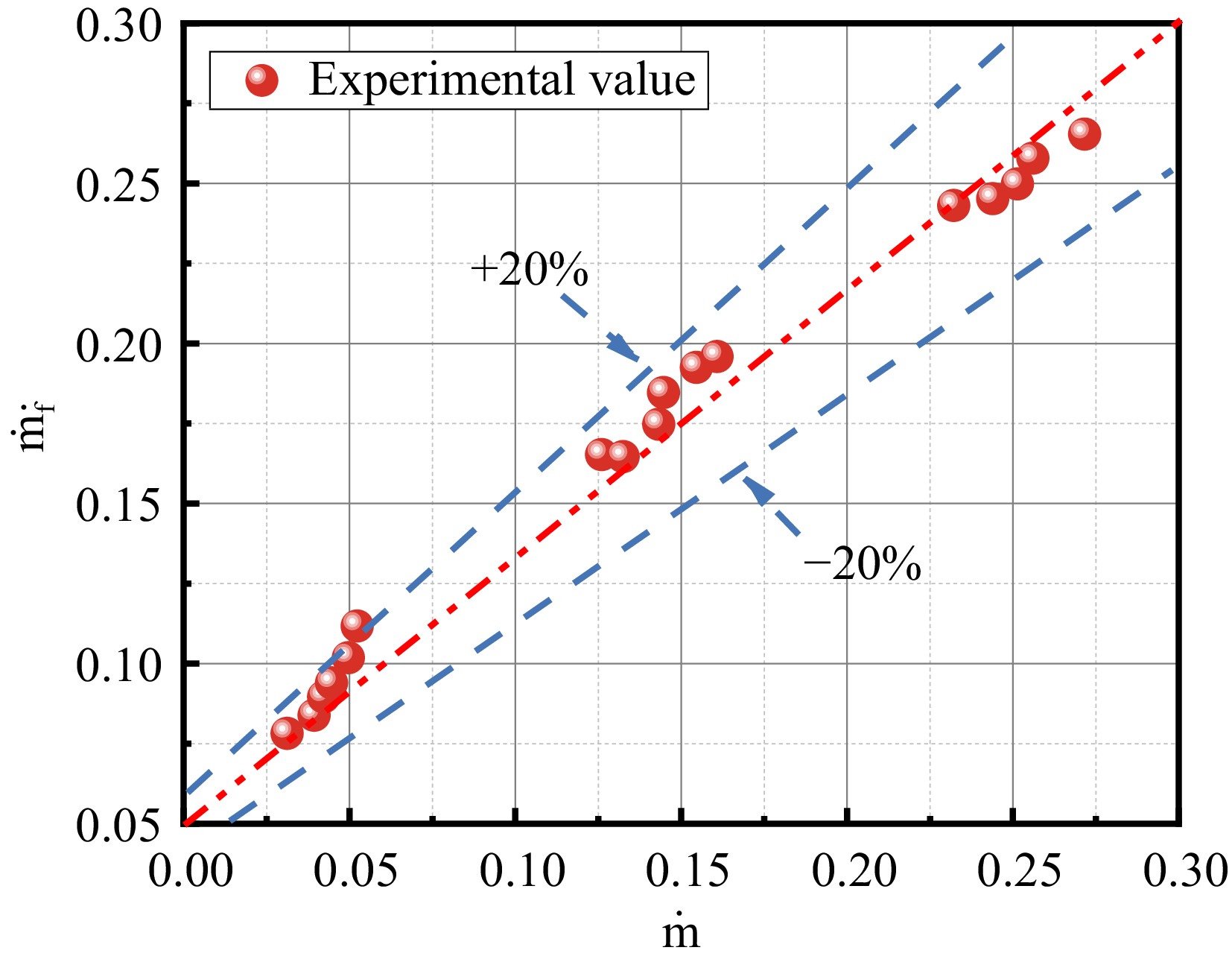
      Parameters Characteristic Numerical value
      B Atomic weight of an element 1.32
      cp Specific heat capacity 1.207 kJ/(kg-K)
      kw Heat conductivity 0.091 W/(m-K)
      Pr Prandtl (math.) 0.073
      Tf Flame temperature 1,400 K
      Tp Pyrolysis temperature 623 K
      α Thermal diffusivity 168 × 10 m−62 /s
      v Kinematic viscosity 121 × 10 m−62 /s

      The mass loss rate vs sample width is shown in Fig. 11, and the results are all for the flame in the stabilization phase, as shown in Fig. 10 after 450 s. The mass loss rate is the average value of the curve. For the same conditions, the mass loss rate shows an increasing trend with the increase of the sample width, which is because the increase of the sample width increases the area of the flame of the material in contact with the air, increasing the mass loss rate. Jiang et al.[8] summarized the mass loss rate ˙mf (g/s) prediction formula, i.e:

      Figure 11. 

      The relationship between mass loss rate and width.

      ˙mf=BkwScpD{0.825+0.387Ra1/6L[1+(0.492/Pr)9/16]8/27}2 (2)

      In addition to what is in the Table 3, the Ra Reynolds number[20] in the above equation can be expressed as:

      RaL=gβ(Tf−T∞)D3vα (3)

      β is the coefficient of thermal expansion (CTE). During the upward spread of the flame, the entire surface of the material burns, and the area of the material exposed to the flame consists of two parts, one of which is the front surface, and the other is the four regions at the edges of the material block, which can be expressed by the following equation:

      Stotal=3 × (WL+2TL+2TW) (4)

      In the above equation, the Stotal is the area of the solid surface region, and W is the width of the material, and T is the material thickness, and L is the material length, as shown in Fig. 12.

      Figure 12. 

      Schematic diagram of solid area parameters.

      In the field of flame, for irregular fuel shapes, it is common to use a characteristic length transformation method to evaluate the flame dynamics behavior. The most commonly used method is the equivalent diameter method. This method typically converts rectangular and other irregularly shaped fuels to the equivalent diameter of a circle. However, this method is only applicable to conditions that have approximately the same length and width. The length of the material in this experiment is much larger than the width, so the equivalent diameter method is not applicable. The method of combining previous definitions of force diameters is used to solve the problem of irregular fuel shapes[21,22]:

      D=2L(W+2T)/L+W+2T (5)

      Substituting the above equations, we can find the ˙mf of the predicted equation, and compare it with the experimentally obtained stable combustion rate ˙m The comparison is shown in Fig. 13. From Fig. 13, it can be seen that the prediction curve is over-predicting the experimental value for condition A. The main reason is that the above equation does not take into account the mass flow rate of heat loss, which leads to a large calculated value. For condition C, the experimental value is larger than the predicted value, and the degree of deviation increases with the increase in the number of PMMA blocks. In this paper, it is argued that although the mass of heat loss is not accounted for in the calculation formula, the experimental values are larger than the predicted values because as the flame develops, the air spacing between the discrete materials provides more oxygen for combustion, and the heat transfer mechanism changes from being dominated by heat loss to being dominated by the air entrainment, which is further evidence that reasonable air spacing between the discrete solids accelerate the rate of the material's mass loss.

      Figure 13. 

      Comparison of predicted mass loss rate data with experimental data.

      Rate of heat release

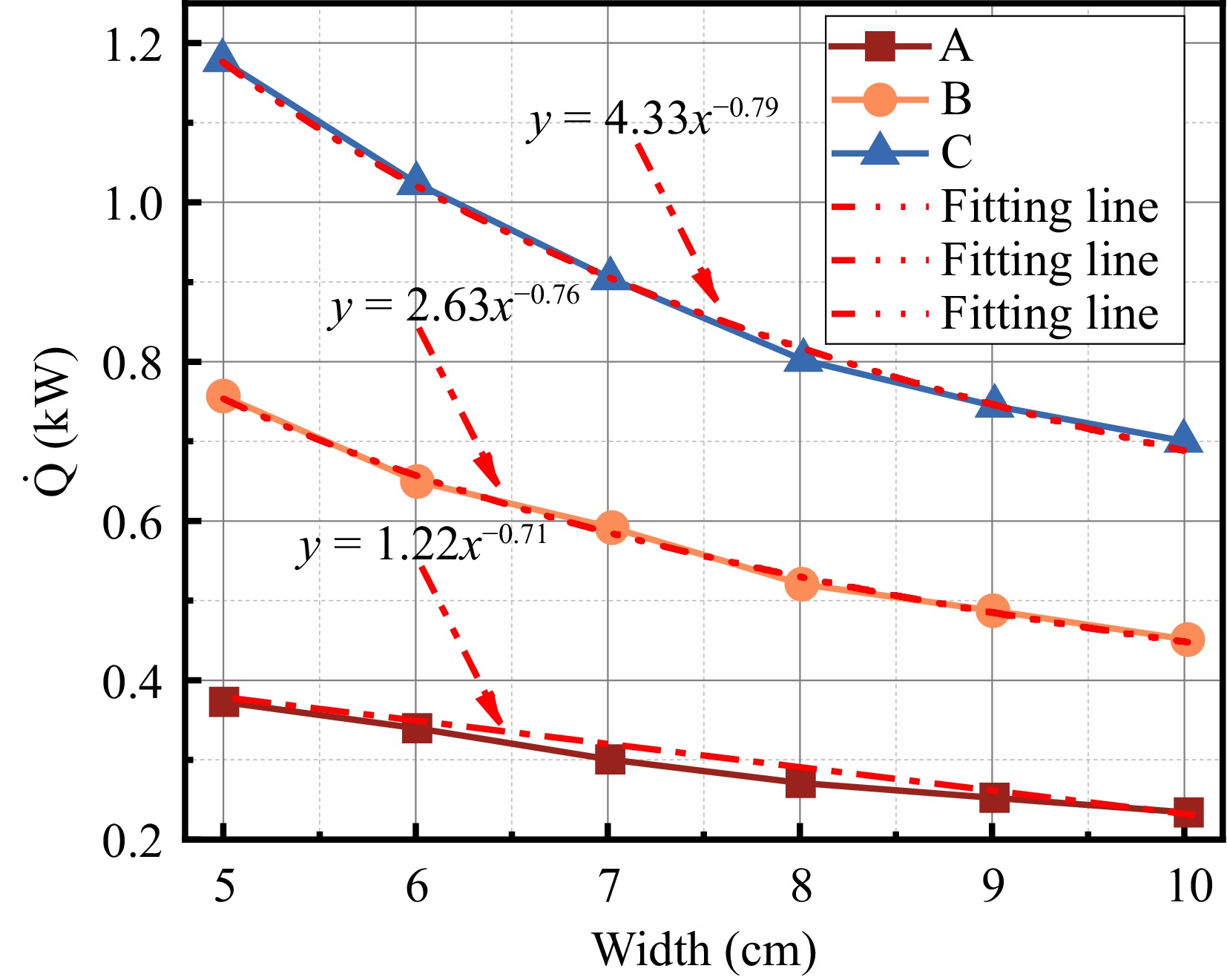
    • Width effects on flame spread include lateral diffusion of gaseous fuels, heat loss, and air entrainment. To better compare width effects on the discrete flame spread, this section focuses on analyzing the unit width heat release rate ˙Q of the flame. According to a previous research summary[23], the rate of heat release per unit width can be obtained from the rate of mass loss. ˙Q can be found from the mass loss rate, i.e.:

      ˙Q=(˙m/w)ΔHc (6)

      In the above equation, ˙m is the mass loss rate, g/s; w is the width of the material; ΔHc is the heat of combustion of the material, this paper takes 25.2 kJ/g. The calculated heat release rate per unit width ˙Q is exponentially fitted with the width W, ˙Q∼Wn.

      As can be seen from Fig. 14, the effect of width on the heat release rate shows approximately the same pattern as the effect of width on the average flame height in the previous section, i.e., the heat release rate decreases with increasing width in a negative power law relationship. Laterally, for increasing width, the heat release rate ˙Q The main reason for the decrease is due to the decrease in the lateral diffusion of fuel and heat; vertically, for the increase in the number of blocks, the increase in the rate of heat release of the material is mainly due to the full development of the flame spread of the discrete solids, so that the air convolutes more oxygen into the flame and pushes the unburned fuel to the center of the material, increasing the rate of combustion of the pyrolysis region.

      Figure 14. 

      The relationship between heat release rate and width.

      Theoretical analysis of material width in open space and discrete flame spread

    • Rangwala et al.[11] and Pizzo et al.[24] The theory proved by the study focuses on the laminar flame without sidewalls (width of 200 mm), which has relatively large pyrolysis products and heat loss around the sidewalls. Rangawala et al.[11] combined mathematical models and experimental results to analyze the effect of finite width on the flame-spreading tendency, and established a simplified physical model of laminar flames, as shown in Fig. 15. In Fig. 15, the X-axis is the direction of the flame spread, the Y-axis is the direction of flame thickness on the surface of the material, the Z-axis is the direction of the width of the material, the ˙m′f(x) is the mass released in unit time, and ˙m′z(x) is the mass lost within XY unit moment, and Xp is the length of pyrolysis, and δf is the flame thickness.

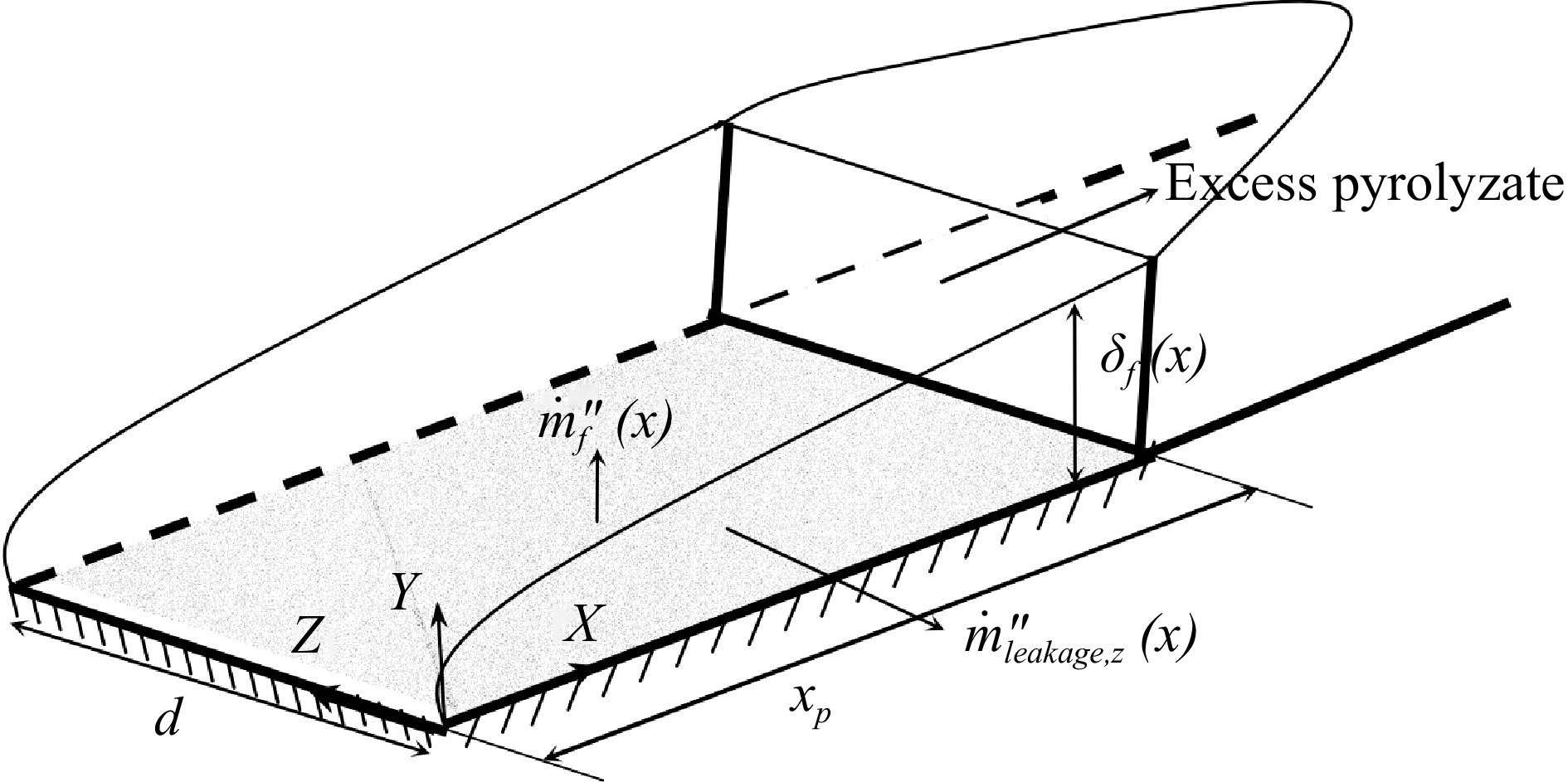
      Figure 15. 

      Physical model of width-influenced flame spread[24].

      Rangawala et al.[11], through theoretical analysis, has made the following statement about the effective rate of combustion ˙M′ is expressed as follows:

      ˙M′=˙M′f−xpw/2˙M′z (7)

      Where, ˙M′f is the solid fuel mass loss rate, and by integrating the ˙m′f(x) and the position of the pyrolysis front, the mass loss per unit area per unit time can be obtained and can be expressed as:

      ˙M′f=∫xp0˙m′f(x)dx (8)

      ˙M′z is the rate of heat loss, the total mass lost by diffusion in the z-direction (i.e., lateral diffusion) and can be obtained by integrating between the fuel surface and the flame position:

      M′z∫δf0˙m′z(x)dy=∫ηf0˙m′z(x)dη (9)

      It can be seen from the formula that when the width of the specimen is small, the heat loss of the specimen spreading to the transverse direction is large and becomes a non-negligible part, which not only reduces the number of gases involved in the combustion reaction but also reduces the transfer of heat to the center thickness region.

    Conclusions

    • In this study, an experimental platform was established to investigate the influence of material width on the behavior of discrete flame spread in open space. Utilizing discrete materials with widths ranging from 5 to 10 cm and fixed spacings, the stabilization phases of the flame spreading process were meticulously analyzed. Key metrics such as mass loss rate, flame height, pyrolysis front, flame-spreading rate, and heat release rate were measured under various conditions. These parameters helped elucidate the impact of specimen width on the dynamics of discrete flame spread. The findings confirm that the width of the material significantly affects the flame behavior, providing a quantifiable relationship between material dimensions and flame dynamics. The key conclusions drawn from the data are as follows:

      (1) The discrete flame spreading pattern shows that as the width of the specimen increases, the flame-burning area increases, the flame brightness becomes brighter, and the brightness of the edge region on both sides is larger than that of the center region; meanwhile, it is found that the width does not have much influence on the discrete flame frontal pattern, which all show the phenomenon of laminar flow at the bottom and turbulent flow at the top.

      (2) In the flame stabilization stage, the dimensionless flame height and the heat release rate per unit width show the same trend, i.e., they show a negative power-law decay relationship with the width, and from the experimental results, the value of the exponent n is in the range of 0.6 to 0.8. At the same time, since the air spacing of the discrete materials provides more oxygen for combustion, the mass loss rate in the stabilization stage is gradually higher than that predicted by the increase in the number of blocks of the discrete materials. predicted value.

      (3) Mathematical analysis of the effect of width on flame behavior led to the conclusion that the heat loss mass flow rate decreases as the width increases, and when the width is greater than the critical width, the width has a negligible effect on the flame spreading behavior. It was found that the 10 cm width did not reach the critical width.

    Author contributions

    • The authors confirm contribution to the paper as follows: study conception and design: Wu Z Peng M; data collection: Wu Z, Zhou J, Qin D, Ma P; analysis and interpretation of results: Wu Z, Chen F, Zhu G; draft manuscript preparation: Wu Z, Li D, Miao W. All authors reviewed the results and approved the final version of the manuscript.

    Data availability

    • All data generated or analyzed during this study are included in this published article.

      Acknowledgments

      • This work was supported by Key R & D programs (No. 2023YFC3009900); The National Natural Science Foundation of China (No. 52204254); The Natural Science Foundation of Jiangsu Province (No. BK20221124); Science and Technology Program of the National Fire and Rescue Administration (No. 2023XFCX33) [Research on high efficiency and environmental protection aerogel foam fire extinguishing agent and its supporting application technology]; Project of 'Double First-class' Construction and Enhancement of Self-innovation Capability: 'Safety Discipline Cluster - Fire and Public Safety' (2022ZZCX05K05); Jiangsu Science and Technology Program (No. SBE2023710026), and Shandong Key Technology Research and Development Program (No. 2021CXGC011303). National Fire and Rescue Service Science and Technology Plan Project 'Firefighters Occupational Health Protection Technology Research' (No. 2020XFLR43); 'Key technical research and application of the smart emergency rescue and management platform' funded by Jinan city (No. 202228052)

      Conflict of interest

      • The authors declare that they have no conflict of interest.

      Rights and permissions
      • Copyright: © 2024 by the author(s). Published by Maximum Academic Press on behalf of Nanjing Tech University. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
    Figure (15)  Table (3) References (24)
  • About this article
    Cite this article
    Wu Z, Zhu G, Peng M, Chen F, Chai G, et al. 2024. Experimental study on the influence of material width on discrete fire spread in open space. Emergency Management Science and Technology 4: e014 doi: 10.48130/emst-0024-0014
    Wu Z, Zhu G, Peng M, Chen F, Chai G, et al. 2024. Experimental study on the influence of material width on discrete fire spread in open space. Emergency Management Science and Technology 4: e014 doi: 10.48130/emst-0024-0014
    shu

Catalog

  • HTML

  • Introduction
  • Experiments
  • Results and discussion

  • Analysis of the influence of width on discrete flame morphology

  • Width affects flame morphology
  • Comprehensive analysis

  • Analysis of the influence of width on the stability stage of discrete flame spread

  • Flame height
  • Rate of mass loss
  • Rate of heat release

  • Theoretical analysis of material width in open space and discrete flame spread

  • Conclusions
  • Author contributions
  • Data availability
  • Acknowledgments
  • Conflict of interest
  • Rights and permissions
  • About this article
logo

Contents

Policies

Services

Partnerships

© 2025 Maximum Academic Press, except Open Access articles. MAP is a member of ALPSP, COPE, CrossRef, cOAlition S, OASPA and STM.

Privacy Policy  |  Site Map  |  Terms and Conditions

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return