-
When dealing with natural or technological risks and resilience, it is of major importance to be able to evaluate the residual capacity of a partially damaged structure (buildings of industrial facilities) in the aftermath of an extreme event, such as earthquakes, floods or explosions[1−6].
In the case of post-quake damage evaluation, this residual capacity evaluation is requested for decision-making. Actually, after inspection and evaluation of the buildings, the civil engineers (and trained technical staff and architects) have to classify the buildings damage into given categories: slight damage (buildings can remain in service), moderate or important damage (buildings need to be evacuated until more detailed evaluation and adequate strengthening take place), or very serious damage (buildings have to be demolished). In the present case, only structural component influences are investigated, regardless of the secondary elements, which influence also the reconstruction and repair costs[1−23].
In the first paper, a theoretical method was developed. The evaluation of the global damage relies on several steps:
● First step – Evaluate the individual damage at each story according to the damage suffered by its constitutive components (beams and columns): The damage of the k-th story, among Ns stories along the building height, becomes:
$ {D}_{s,k}=1-\left\{\prod _{i=1}^{{N}_{B}}{(1-{D}_{b,i})}^{{\alpha }_{b,i}}\right\}.\left\{\prod _{j=1}^{{N}_{C}}{(1-{D}_{c,j})}^{{\alpha }_{c,j}}\right\} $ (1) where, Ds = story damage; Db = beam damage; Dc = column damage; NB and NC = number of beams and columns at the k-th story, respectively; αb and αc = importance factors for the beams and columns, respectively.
● Second step – Global damage of the structure: The global damage of the structure depends then on the story's importance factor βk, so that:
$ {D}_{G}=1-\left\{\prod _{k=1}^{{N}_{S}}{(1-{D}_{s,k})}^{{\beta }_{k}}\right\} $ (2) where, DG = global damage of the building; β = importance factor for the current story, which depends on its location along the building height, since the lower levels have more influence than the upper levels in the case of similar damage levels.
In order to validate the methodology and the adopted values for the importance factors α and β, the present paper investigates the efficiency and accuracy of the theoretical prediction. The predicted values of the global damage are compared to those obtained by a mechanical analysis of the buildings response under real seismic inputs.
-
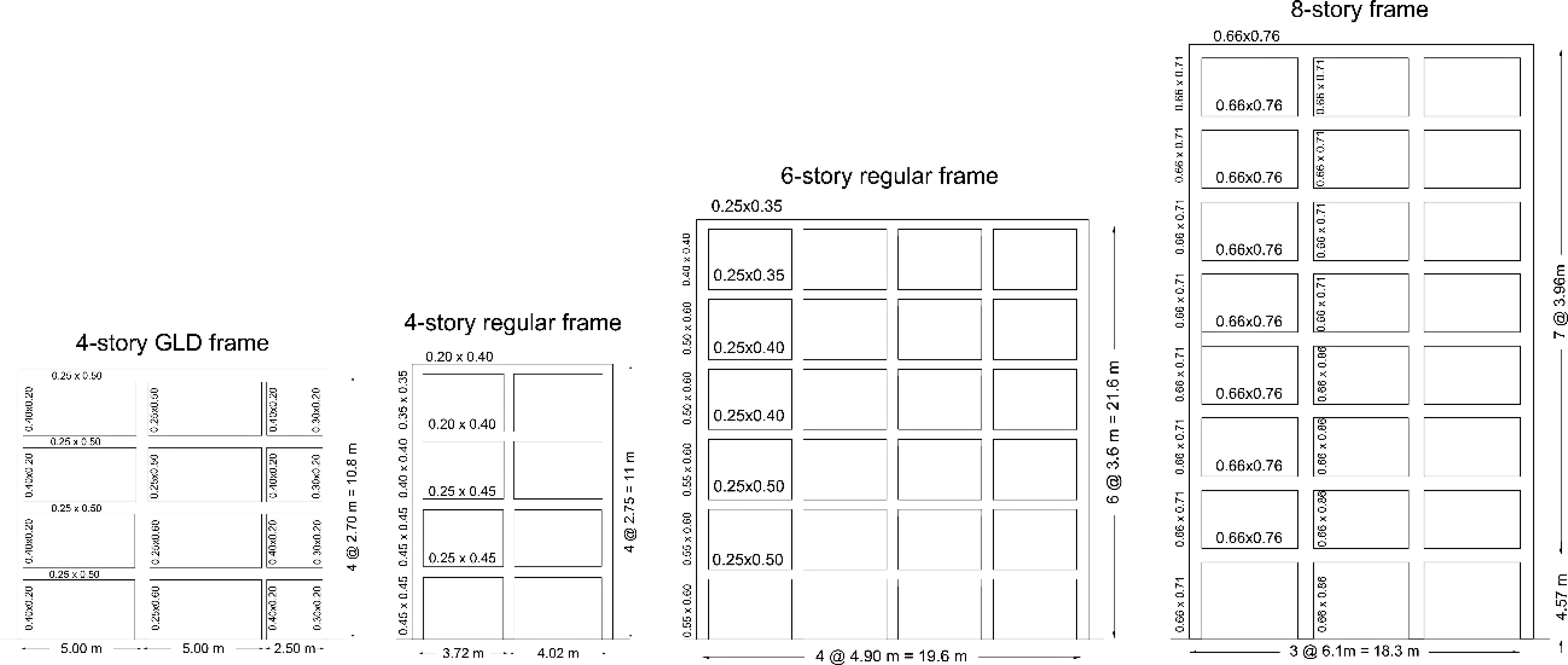
For validation purposes, various patterns of components damage in the case of four current RC frames typologies, regardless of their use limitations in some countries, are investigated, see Fig. 1:
● A 4-story GLD frame (Gravity Load Frame);
● 4- and 6-story buildings designed for seismic loads typical of high seismic risk areas;
● 8-story frame collected from a study about seismic collapse safety in modern RC buildings[16].
The numerical models are simulated using the OpenSees platform, under the following assumptions[17]:
● P-delta effects are considered.
● Soil-structure interaction is not taken into account. Hence, the supports are modelled as infinitely rigid.
● The nonlinear behaviour of the structural elements is modelled through an embedded distributed plasticity model, the 'nonlinear beam Column' element. The moment-curvature relationships are obtained from a fiber element analysis over each element. They are approximated by bilinear curves and modelled by an available hysteretic model.
After occurrence of earthquakes, the global damage are, in general, classified into five damage categories with some typical colors as tags: No damage (Light Green tag), Slight damage (Dark Green tag), Moderate damage (Light Orange tag), Severe damage (Dark Orange tag) up to Collapse/Complete damage (Red tag)[1−10,12].
To investigate the efficiency of the proposed methodology, the present study considers various damage patterns resulting from some potential combinations of column and beam damage. Thus, two levels of component damage are considered:
● Low-to-Medium level (LM), supposed to range between 0.10 and 0.40 (from green up to orange tags);
● Medium-to-High level (MH) supposed to range between 0.4 and 0.8 (from orange up to red tags).
-
To investigate the story effect, various values of the importance factor β are adopted as it expresses the story influence on the global damage. However, it is worth remembering that the columns and beams contributions are expressed through their influence factors, αb and αc at each story.
Of course, the role of the story in the global damage depends on both its location and number of upper stories. Intuitively, lower stories have a more important contribution on the global damage than the upper levels. Columns failing at the lowest story will produce immediate collapse of the whole building, whereas failure at the top story produces only local collapse, so that the lower stories can still remain under service.
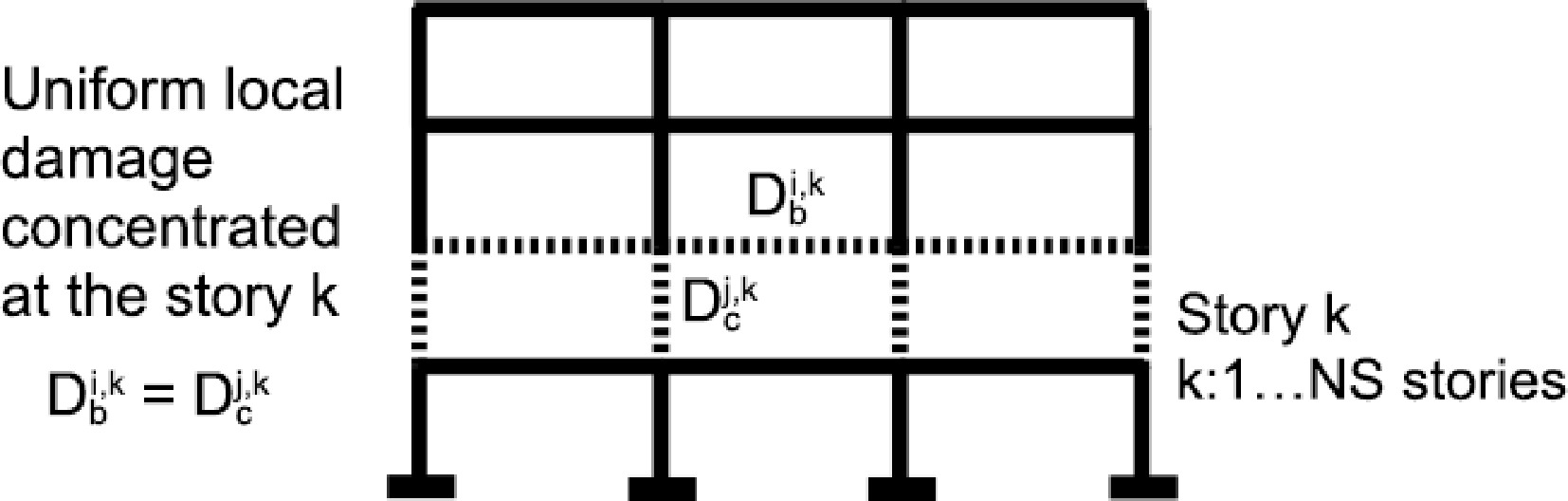
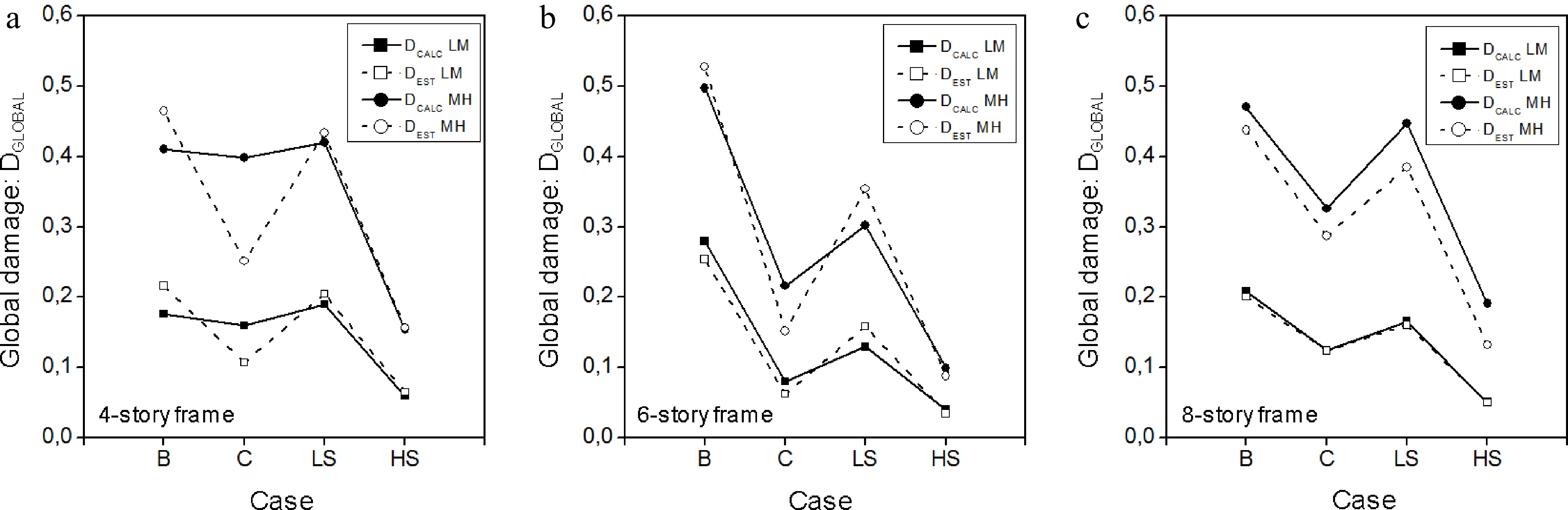
For the story sensitivity analysis, the following assumptions are adopted, see Fig. 2.
● All the beams and columns, at the considered story, are supposed to have the same damage, i.e. the damage level is uniform for the whole story components.
● The components damage at the story are then: Dc = Db = 0.30 for Low-to-Medium level (LM), and Dc = Db = 0.60 for Medium-to-High levels (MH) of damage, so that the story damage is, respectively, Ds = 0.30 and 0.60 at the current k-th story.
Analysis of influence factor β
-
The sensitivity analysis of the global structural damage due to the story damage is performed as follows:
● The damaged story location is successively considered for the lowest up to the highest level. The story at the current location is supposed to be damaged whereas the others are all supposed to suffer no damage, see Fig. 3.
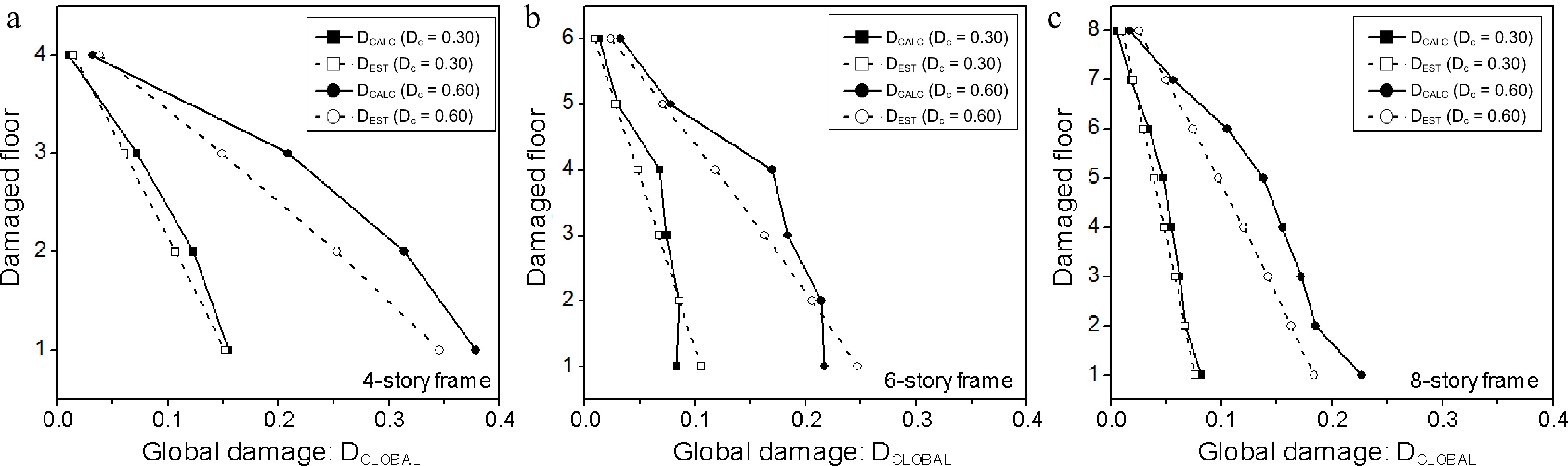
● At each location, the global damage (DEST), obtained by the methodology, is compared to the simulation results (DCALC) provided by the OpenSees run (Fig. 4).
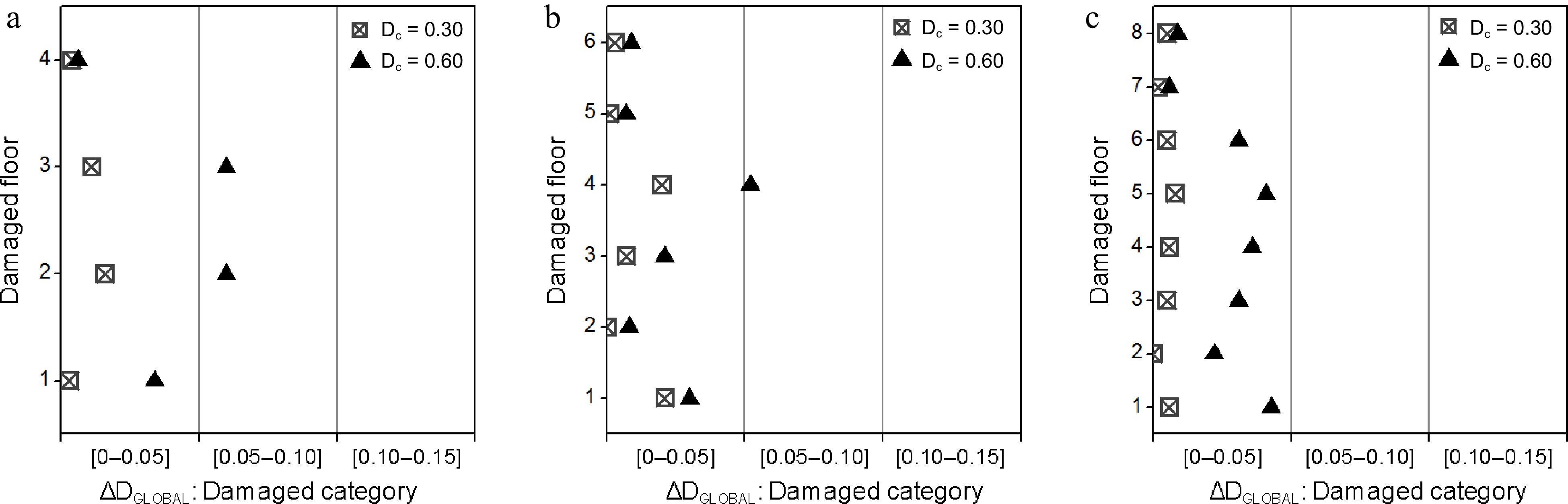
Figure 4.
Classification of ΔDGLOBAL according to the damage category: (a) 4-story; (b) 6-story; (c) 8-story frames.
The obtained results show that (Fig. 4):
● For Low-to-Medium levels of damage, the methodology prediction (DEST) is in good accordance with the simulation results (DCALC).
● For Medium-to-High levels of damage, the methodology prediction (DEST) underestimates the global damage as the simulation results (DCALC) are considered as the reference values. However, one could consider these results as acceptable since the hypothesis that damage is concentrated only in one story, whereas its neighbor stories are damage free may not be a common configuration in real situations. It might be expected that smooth variation from one story to the next would be more realistic.
Moreover, when using global damage values to classify structures according to the damage categories (e.g. Slight, Moderate, Severe, Complete damage), the associated damage ranges in these categories are normally wide enough, e.g. Slight damage is considered when the global damage value is between 0.0 and 0.10. Therefore, considering the differences between calculated and estimated damage (ΔDGLOBAL), one could observe that for most cases they do not differ by one damage category level (upper or lower), even for strict definition of a category, i.e. a difference of 0.05 of the damage values.
Except for three singular cases, the obtained results, i.e. both predicted and simulated, fall within the same category: a difference less than 0.05 of the damage values, see Fig. 4. It is worth noting that other existing methods, such as the probabilistic approach for instance, would have concluded that there is no change in the damage category for such a small difference between the predicted and simulated damages[1−4].
Therefore, it can be concluded that the β factor, adopted in the present study, seems to be relevantly defined and calibrated. It efficiently reflects the importance of the damaged story position on the global damage: the lowest stories have the highest effect.
Component beams and columns effects: analysis of their importance factors α
Damage patterns and operational procedure
-
Besides the story effect, which depends on its location within the building height, the story damage level is intimately depending on the damages suffered by its structural components, i.e. beams and columns. Their contributions, to the story damage, are expressed through their respective influence factors, αb and αc.
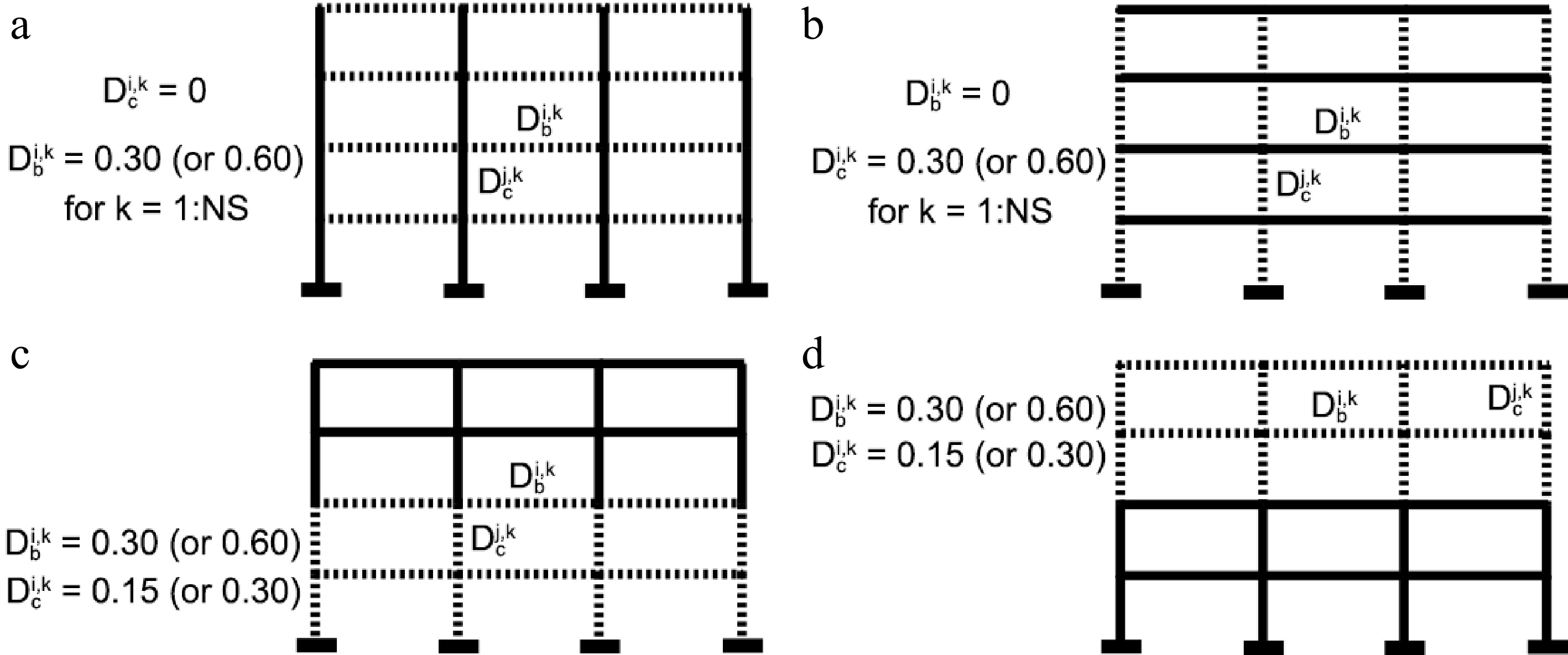
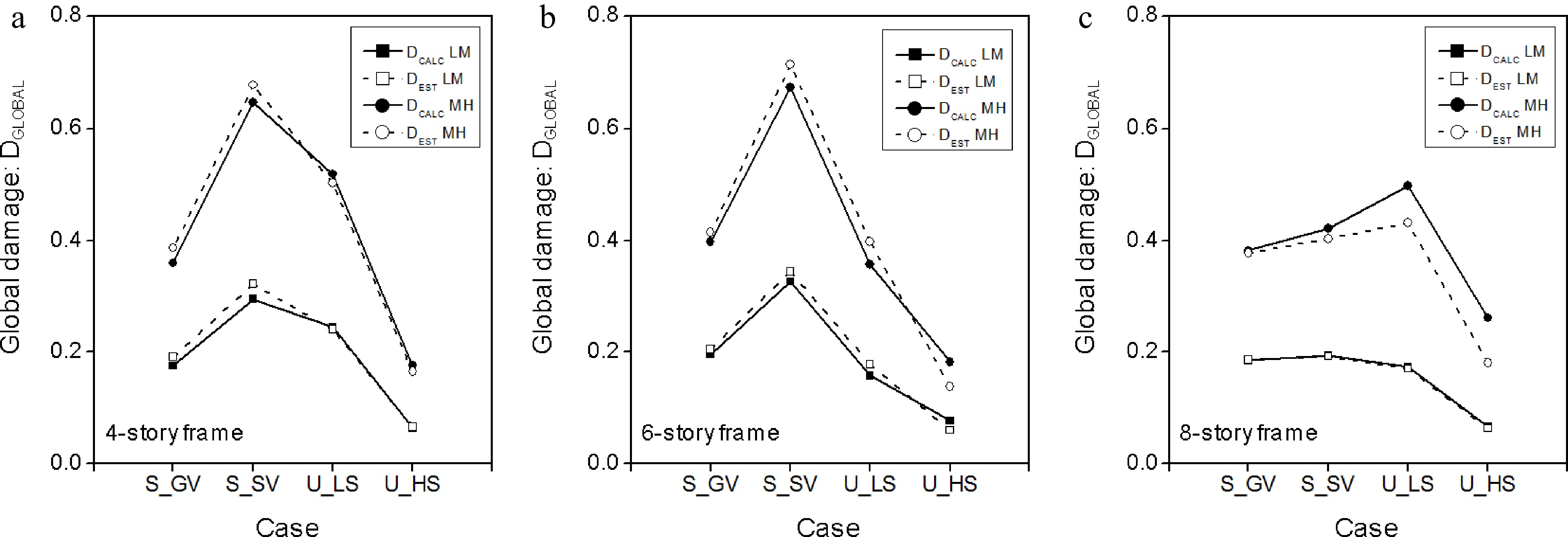
Four particular damage patterns are considered, for illustrative purposes. For the story sensitivity to its beams and columns damages, the following assumptions are thus adopted, see Fig. 5.
● Case 'a': All the beams are supposed to suffer the same damage value along the whole building: Db.
● Case 'b': All the columns are supposed to suffer the same damage value along the whole building: Dc.
● Case 'c' or 'LS': All the columns and beams are supposed to suffer the same damage value along the two lowest stories: Db = Dc.
● Case 'd' or 'HS': All the columns and beams are supposed to suffer the same damage value along the two highest stories: Db = Dc.
● For each of the four particular damage distributions within the building, two damage levels are adopted for the components: Dc = Db = 0.30 for Low-to-Medium level (LM), and Dc = Db = 0.60 for Medium-to-High levels (MH) of damage.
Analysis of influence factors α
-
Except for a singular configuration (case 'c' with Medium-to-High damage level) of the 4-story frame, the proposed approach estimates correctly the resulting global damage category, the analytical results provided by the simulation run (OpenSees) being the reference damage values, see Fig. 6. Furthermore, the differences range, once again, within acceptable limits, all being near the first damage category, except for the singular case (case 'c' for the 4-story frame), see Fig. 7.
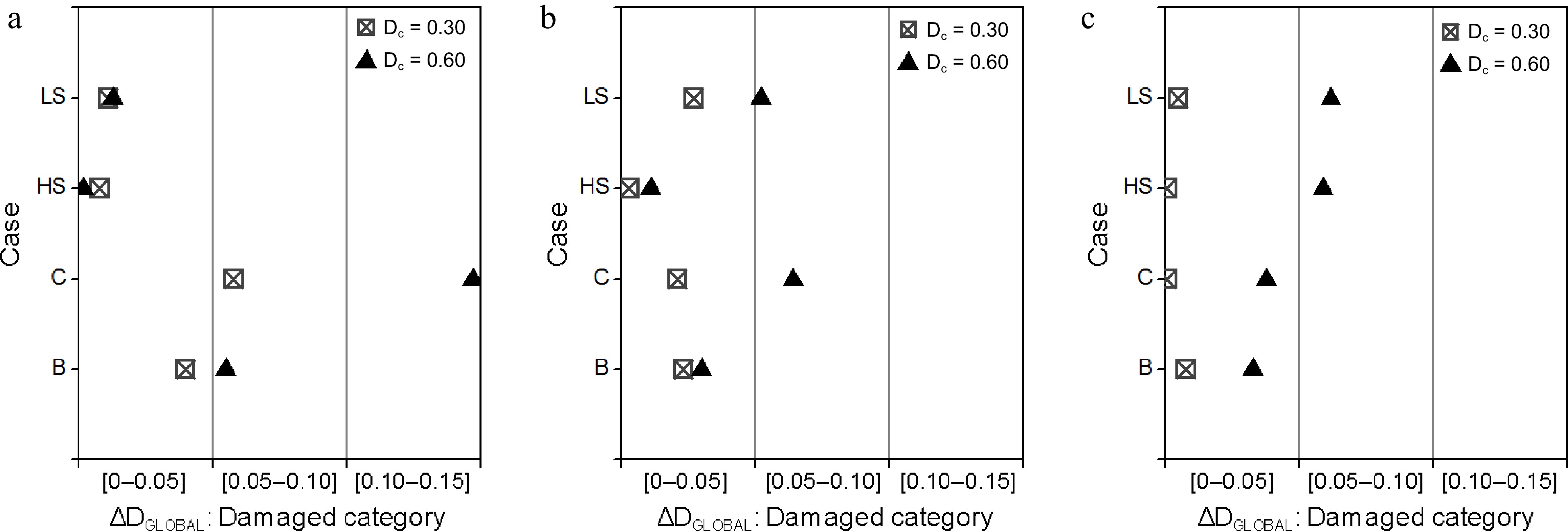
Figure 7.
Difference between DCALC and DEST according to the damage category: (a) 4-story; (b) 6-story; (c) 8-story frames.
Therefore, it can be concluded that the α factors, adopted in the present study, seems to be relevantly defined and calibrated. They efficiently reflect the influence of the beams and column damage story position on the global damage.
Combined beams, columns, and story location effects: global combination
Damage patterns and operational procedure
-
In real cases, it is seldom that the beams and columns will suffer the same damage level during an earthquake. Actually, due to the materials heterogeneity, the random values of the live and dead loads, as well as the stochastic seismic input and structure response, it is unlikely that the structural components as well as the connected secondary components (fillings, stairs, balconies, etc.) will be uniformly damaged, even at a the same story level[1−4].
Four scenarios for the damage patterns are investigated, for illustrative and validation purposes, see Table 1 for the case of a 6-story frame example.
Table 1. Damage pattern of the 6-story frame, for low-medium (LW) levels of damage.
Event Damage Story Beam Columns 1 2 3 4 1 2 3 4 5 S_GV 1 0.25 0.25 0.25 0.25 0.15 0.15 0.2 0.15 0.15 2 0.25 0.25 0.25 0.25 0.15 0.15 0.2 0.15 0.15 3 0.2 0.2 0.2 0.2 0.15 0.15 0.2 0.15 0.15 4 0.2 0.2 0.2 0.2 0.1 0.1 0.15 0.1 0.1 5 0.1 0.1 0.1 0.1 0.1 0.1 0.15 0.1 0.1 6 0.1 0.1 0.1 0.1 0.1 0.1 0.15 0.1 0.1 S_SV 1 0.4 0.4 0.4 0.4 0.2 0.2 0.2 0.2 0.2 2 0.4 0.4 0.4 0.4 0.2 0.2 0.2 0.2 0.2 3 0.4 0.4 0.4 0.4 0.2 0.2 0.2 0.2 0.2 4 0.3 0.3 0.3 0.3 0.1 0.1 0.1 0.1 0.1 5 0.3 0.3 0.3 0.3 0.1 0.1 0.1 0.1 0.1 6 0.3 0.3 0.3 0.3 0.1 0.1 0.1 0.1 0.1 U_LS 1 0.4 0.2 0.15 0.35 0.3 0.35 0.25 0.2 0.3 2 0.35 0.25 0.15 0.3 0.25 0.25 0.2 0.1 0.25 3 0.15 0.1 0.2 0.2 0.15 4 0.1 0.1 5 6 U_HS 1 2 3 0.1 4 0.2 0.1 0.2 0.25 0.2 0.25 0.25 5 0.35 0.2 0.3 0.2 0.3 0.3 0.3 0.2 0.1 6 0.15 0.15 0.2 0.15 0.15 0.25 0.2 0.15 ● Case 'S_GV': Symmetric distribution of the damages at a story and gradual variation from the lower to the upper stories. The beams have the same damage at the given story. For the columns, the central column may suffer different damage than the external columns. In general, it is observed that the lower stories suffer more damage than the upper levels.
● Case 'S_SV': Symmetric distribution of the damages at a story and sharp variation from lower to the upper stories. The beams have the same damage at the given story. The columns are also supposed to suffer a unique damage level either at the central or external position within a given story.
● Case 'U_LS': Unsymmetrical distribution of the damages at a story level. The beams as well as the columns have arbitrary damage levels. The damages are supposed to be located at the lower stories.
● Case 'U_HS': Unsymmetrical distribution of the damages at a story level. The beams as well as the columns have arbitrary damage levels. The damages are supposed to be located at the higher stories.
Concerning the damage distribution within the building, two ranges of the damage levels are investigated i.e. Low-to-Medium level (LM), i.e. Dc and Db range within the intervals [0.1 ... 0.4] and Medium-to-High level (MH), i.e. Dc and Db range within the intervals [0.4 ... 0.8].
Results and analysis
-
The obtained results show that the proposed methodology derives with acceptable accuracy the global damage from the damage of the structural components, i.e. the beams and columns located at any story being at upper as well as lower levels within the building, see Figs 8 & 9. Furthermore, the method efficiency is better for the case of uniform damage patterns at a story, which is typical of real situations.
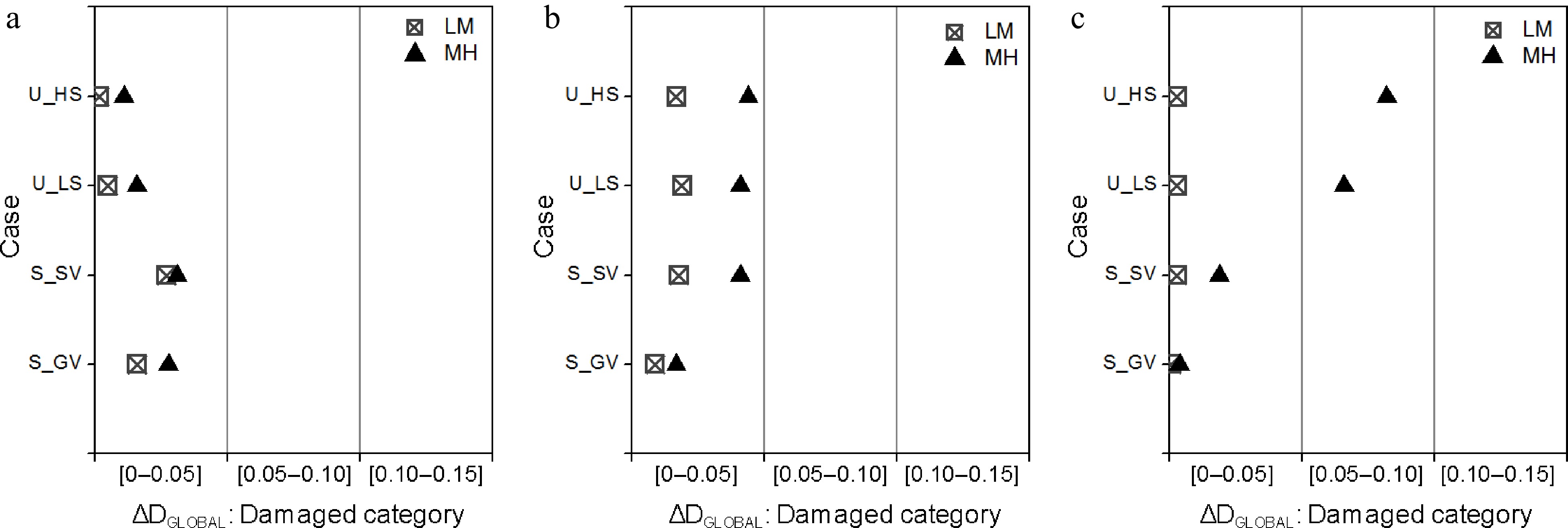
Figure 9.
Difference between DCALC and DEST according to the damage category: (a) 4-story; (b) 6-story; (c) 8-story frames.
Therefore, it can be concluded that the α as well as the β factor definition, adopted in the present study, seems to be relevantly defined and adequately calibrated. They efficiently reflect:
● the influence of the beam and column damage for the evaluation of the concerned story damage;
● the importance of the story position on the building global damage.
-
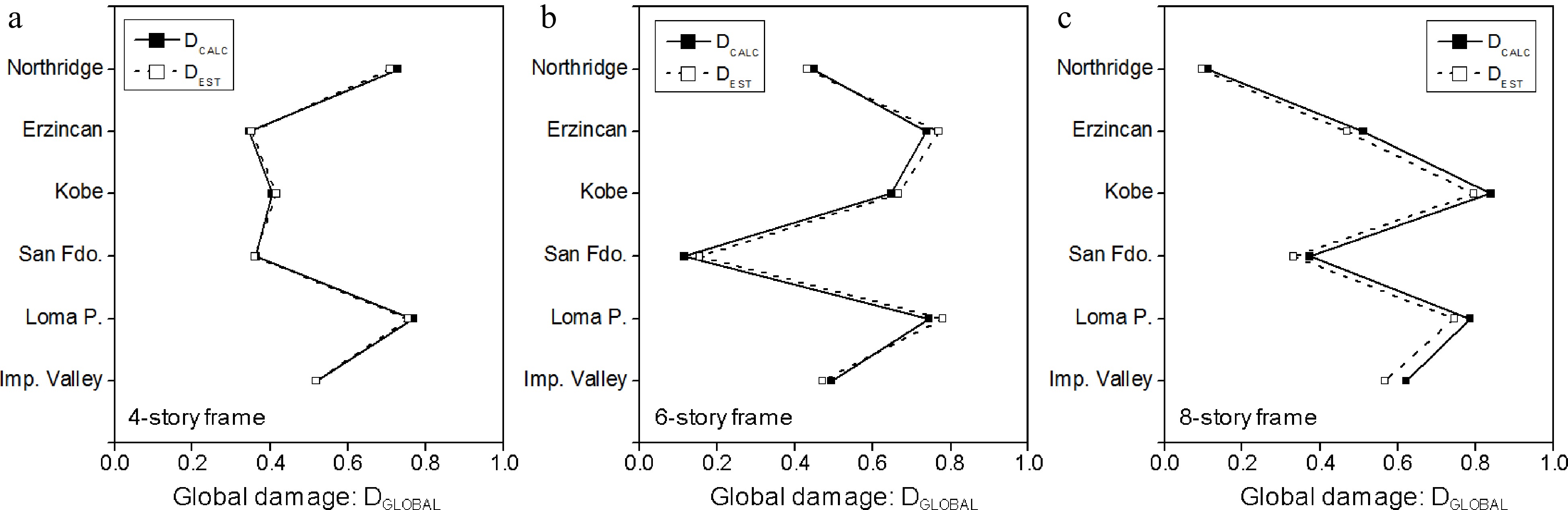
For final validation purposes, real seismic scenarios are considered, see Table 2. These six scenarios are arbitrarily chosen as they are used worldwide as historic references. Therefore, they are not normalized (to an equal PGA value, for instance) but are rather considered as they were recorded and available. Under each ground motion, the seismic response of each selected building is investigated. The dynamic analysis, run under OpenSees software, provides the damage at each of the beams and columns along the whole structure.
Table 2. Ground motion events selected for the validation analysis.
N Earthquake Year Station (component) Mw PGA (g) 1 Imperial Valley 1940 El Centro (180) 7.0 0.31 2 Loma Prieta 1989 Corralitos (000) 6.9 0.64 3 San Fernando 1971 Castaic (021) 6.6 0.32 4 Kobe 1995 Takaratzuka (000) 6.9 0.69 5 Erzincan 1992 Erzincan (NS) 6.9 0.52 6 Northridge 1994 Canyon country (270) 6.7 0.48 Seismic damage calculated for the selected buildings
-
After the simulation run, each component (either beam or column) is assigned the maximum damage observed along the considered component.
These damage distributions are, afterwards, used as input values, i.e. individual beam or column damage value, for the proposed methodology, as shown in Tables 3−5, for the 4-story, 6-story, and 8-story frames, respectively.
Results analysis and discussion
-
A wide variety of damage distributions has been obtained after simulation of the building’s seismic response. The structural behavior and the subsequent damage depend, obviously, on the input (ground motions) as well as the typology and materials of the buildings. For instance, for the 4-story building case, the patterns are, as expected, unsymmetrical and decreasing along with the building height, as shown in Table 3.
Table 3. Examples of damage arrangements obtained for the 4-story frame.
GM Damage Story Beam Colunm 1 2 1 2 3 Erzincan 1 0.68 0.51 0 0.32 0 2 0.59 0.18 0 0.48 0 3 0 0 0 0.21 0 4 0 0 0 0 0 Loma Prieta 1 0.8 0.84 0.61 0.78 0.62 2 0.85 0.82 0 0.86 0 3 0.79 0.66 0.47 0.89 0.35 4 0 0 0 0 0 In some cases, the damage is either concentrated on a particular section of the building or increases along the building height, as the ground motions may produce predominantly high mode responses. This is, for instance, the case of the 6-story frame, which presents a major change in stiffness between the 5th and the 6th stories, causing therefore a damage concentration at these zones, as illustrated in Table 4.
Table 4. Examples of damage arrangements obtained for the 6-story frame.
GM Damage Story Beam Colunm 1 2 3 4 1 2 3 4 5 San Fernando 1 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 5 0.87 0.87 0.87 0.87 0 0 0 0 0 6 0.52 0.44 0.46 0.55 0 0 0 0 0 Northridge 1 0 0 0 0 0 0 0 0 0 2 0.45 0.41 0.4 0.48 0 0 0 0 0 3 0.5 0.51 0.51 0.52 0 0 0 0 0 4 0.58 0.54 0.54 0.58 0 0 0 0 0 5 0.91 0.91 0.91 0.91 0 0 0 0 0 6 0.78 0.76 0.76 0.78 0 0 0 0 0 For the 8-story frame, various kinds of damage patterns have been observed, from uniform distributions under the Imperial Valley record to concentrations of damage on higher stories under the Northridge record, as shown in Fig. 10 and Table 5.
Table 5. Examples of damage arrangements obtained for the 8-story frame.
GM Damage Story Beam Column 1 2 3 1 2 3 4 Imperial Valley 1 0.78 0.78 0.77 0 0 0 0 2 0.72 0.73 0.7 0 0 0 0 3 0.62 0.67 0.6 0 0 0 0 4 0.74 0.75 0.7 0 0 0 0 5 0.83 0.81 0.8 0 0 0 0 6 0.85 0.84 0.82 0 0 0 0 7 0.8 0.8 0.76 0 0 0 0 8 0 0 0 0 0 0 0 Northridge 1 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 4 0 0.09 0 0 0 0 0 5 0 0.12 0.24 0 0 0 0 6 0.29 0.25 0.21 0 0 0 0 7 0.82 0.79 0.79 0 0 0 0 8 0.55 0.45 0.57 0 0.71 0.64 0 By being able to address a wide range of seismic motions and handle various damage distributions for real motions and current RC building typology, the proposed methodology has demonstrated its capacity in predicting efficiently, and with acceptable accuracy, the global building damage, see Fig.10.
These results confirm that the theoretical methodology as well as its importance factors expressions (α and β factors) are suitable for seismic damage evaluation. Such methodology can then be objectively used to improve the existing evaluation forms, used worldwide for a quick post-quake evaluation of buildings[1−10,12,13].
-
The methodology proposed in this paper aims to derive the global structural damage from the damages observed on its main structural constitutive components, i.e. beams and columns in the case of RC frame buildings.
Global damage refers to the reduction of the stiffness, which governs the global residual capacity of the buildings. The study investigates the effect of the components damages, i.e. beam damage (Db) and column damage (Dc), at each story level. The damage of the current story (Ds) is accordingly derived once the importance factors, αc and αb, are adequately calibrated for these beams and columns. The influence of the story damage depends also on its location along the building height, whose influence is expressed through the importance factor β related to the story location and number of upper stories.
For calibration and validation purposes, various frame buildings typologies (4-, 6-, and 8-story frames) and component damage distribution, Moderate-to-Medium and Medium-to-High damage levels, are considered. Symmetric as well as non-symmetric damage distribution at the current story are also investigated, these damages being located at upper or lower stories.
The methodology predictions are compared to the reference damage values, which are obtained thanks to mechanical simulation and seismic analysis performed by using OpenSees software. The obtained results show that α as well as β factors, adopted in the present study, seem to be relevantly defined and adequately calibrated. They efficiently reflect the influence of the beam and column damage for the evaluation of the concerned story damage, and the importance of the story position on the building global damage.
The validity and efficiency of the proposed method is also investigated in the case of different RC frame typologies (from 4 up to 8 story height) under real seismic motions, that are widely used as reference events in earthquake engineering (records from Erzincan, Loma Prieta, San Fernando, Northridge, Imperial Valley and Kobe worldwide investigated events). The corresponding component damage is non-symmetrically distributed and differently located along the building heights. For instance, some cause more damage at the upper stories whereas others affect the lower stories more.
The proposed method has shown its capacity to tackle a wide range of seismic motions and non-uniform damage distributions for real motions and current RC buildings typology. It efficiently predicts the global building damage with an acceptable accuracy.
The theoretical methodology as well as its importance factor expressions (α and β factors) are suitable for seismic damage evaluation. Such methodology can be helpful in improving the existing evaluation forms. Some existing evaluation forms used worldwide for quick post-quake evaluation of buildings do not differentiate the case of lower or upper story damage, and neither do they differentiate the separate cases of beams or columns, as well as the number of failed or damaged components.
-
The authors confirm contribution to the paper as follows: study supervision and coordination: Mebarki A; theoretical aspects development, methodology, case studies selection, results analysis, writing - draft manuscript preparation: Mebarki A, Jerez S; theoretical aspects validation, simulations (under Opensees and Matlab) run: Jerez S. All authors reviewed the results and approved the final version of the manuscript.
-
All data generated or analyzed during this study are included in this published article.
-
The authors declare that they have no conflict of interest. Ahmed Mebarki is the Editorial Board member of Emergency Management Science and Technology who was blinded from reviewing or making decisions on the manuscript. The article was subject to the journal's standard procedures, with peer-review handled independently of this Editorial Board member and the research groups.
- Copyright: © 2024 by the author(s). Published by Maximum Academic Press on behalf of Nanjing Tech University. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
-
About this article
Cite this article
Mebarki A, Jerez S. 2024. Emergency management and urban resilience under seismic risks. Part II: validation and sensitivity analysis for buildings seismic damage evaluation. Emergency Management Science and Technology 4: e026 doi: 10.48130/emst-0024-0025
Emergency management and urban resilience under seismic risks. Part II: validation and sensitivity analysis for buildings seismic damage evaluation
- Received: 01 August 2024
- Revised: 09 October 2024
- Accepted: 14 October 2024
- Published online: 20 December 2024
Abstract: The present paper follows the first part that aimed to develop a theoretical methodology able to derive building global damage from its structural components' damages: beams and columns in the case of RC frame buildings. This second part performs a validation and sensitivity study. It investigates the individual role of the beams and columns at the story level. It investigates afterwards the influence of the stories according to both their location along the height of the building, and their number. The theoretical predictions of the global damage are compared to reference values, which are obtained thanks to dynamic analysis performed on the OpenSees platform. Various damage distributions are tested: uniform as well as non-uniform damage for the whole components at a current story, symmetric, and non-symmetric damage distribution (at central or external columns), smooth or sharp variation from a story to its neighbors, concentration at upper or lower stories, and moderate or important damage level (low-to-medium or medium-to-high). Real ground motions are used as seismic input in order to investigate the method’s efficiency. The proposed method appears to be efficient, with acceptable accuracy, in the case of RC frame (from 4- up to 8-story height). Through the investigated cases, it can be pointed out that the adopted set of importance factor expressions (α and β factors) are relevant and suitable for seismic damage evaluation. It is worth noting that such methods can be helpful in calibrating and improving the current evaluation forms existing worldwide, for quick post-quake damage evaluation.
-
Key words:
- Emergency management /
- Seismic damage /
- Resilience /
- Buildings /
- Residual capacity /
- Seismic response