-
Malaria is a life-threatening disease that is particularly epidemic in sub-Saharan Africa and South-East Asia. According to the World Malaria Report, approximately 2.2 billion people were at the risk of malaria; of them, an estimated 219 million cases occurred worldwide, and consequently 435,000 people, mostly children, were killed by malaria (World Malaria Report 2018, WHO). Fortunately, artemisinin, a kind of sesquiterpene lactone, which was first found by Chinese scientists from a traditional Chinese herbal plant Artemisia annua, can effectively cure malaria[1]. To date, artemisinin-based combination therapies (ACTs) have been recommended as the first-choice treatment method for drug-resistant malaria by the World Health Organization (WHO)[2, 3]. Besides the anti-malarial effect, artemisinin also exhibits pharmaceutical activities in the treatment of diabetes[4], inflammatory response[5] and tumor[6].
Different strategies were applied for increasing artemisinin supply such as chemical synthesis, semi-synthesis from microbially sourced artemisinic acid, and metabolic engineering in A. annua. Chemical synthesis of artemisinin is difficult and costly. Although a concise synthesis of artemisinin from inexpensive cyclohexanone was reported, which reached the gram scale, there is still quite a lot to do before large-scale production can be achieved[7]. Semi-synthesis of artemisinin has achieved success. Artemisinic acid, the precursor for chemically synthesizing artemisinin, can be biosynthesized through successive enzymatic reactions in engineered yeast cells at 25 g/L, ensuring artemisinin production can reach an industrial scale[8−10]. But the semi-synthesis by yeast is still relatively high in cost and low in production, limiting its extensive application. Therefore, at present, Artemisia annua plants remain the primary source for obtaining artemisinin.
Artemisinin is mainly extracted from A. annua leaves, but its content in wild A. annua is low (0.1%–1% dry weight)[11, 12], unable to meet global demand. It is therefore of great importance to elevate artemisinin production in A. annua and develop new A. annua lines with high yield artemisinin by metabolic engineering and genetic breeding.
Over a decade ago, the artemisinin biosynthetic pathway has been completely elucidated at the molecular level. The precursor for artemisinin biosynthesis is farnesyl diphosphate (FDP) containing three isoprenyl 5-carbon (C5) units, which is formed by the condensation of three isopentenyl diphosphates (IPPs) through the catalysis of farnesyl diphosphate synthase (FPS). Isopentenyl diphosphate (IPP) and its isomer dimethylally diphosphate (DMAPP) are the general 5-carbon precursors for all terpenoids, including monoterpenes, sesquiterpenes, diterpenes and so on. IPP can be synthesized through two distinct pathways in the plant: the cytosolic mevalonate pathway (MVA) and the plastidial methylerythritol phosphate (MEP) pathway[13, 14]. In the MVA pathway, HMG-CoA reductase (HMGR) is the rate-limiting enzyme[15], while in the MEP pathway, DXR is the rate-limiting enzyme[16]. The two enzymes are the preferred target enzymes for metabolically engineering artemisinin biosynthesis in the upstream pathway of artemisinin biosynthesis.
After the formation of FDP, amorpha-4,11-diene synthase (ADS), which is believed to be the first committed step in artemisinin biosynthesis, catalyzes the cyclization of FDP into cyclic amorpha-4,11-diene as the unique precursor for artemisinin[17]. Then a multiple-function enzyme CYP71AV1 converts amorpha-4,11-diene into artemisinic alcohol, artemisinic aldehyde and artemisinic acid sequentially[18]. Subsequently, artemisinic aldehyde is reduced to dihydroartemisinic aldehyde under the catalysis of artemisinic aldehyde Δ11 (13) reductase (DBR2)[19]. Then dihydroartemisinic aldehyde is converted into dihydroartemisinic acid by aldehyde dehydrogenase (ALDH1)[20]. Dihydroartemisinic acid is the direct precursor for artemisinin, which is transformed into artemisinin by photo oxidative reaction without enzymes[21, 22]. Meanwhile, artemisinic acid can be converted into arteannuin B via a photo-oxidative non-enzymatic reaction[21, 22]. The four genes, including ADS, CYP71AV1, DBR2 and ALDH1, which are artemisinin-specific biosynthetic genes, are specifically expressed in glandular trichomes of A. annua[23, 24]. The complete elucidation of the artemisinin biosynthetic pathway provides the biosynthetic genes necessary for engineering artemisinin biosynthesis, and facilitates the development of new A. annua varieties with a high-yield of artemisinin.
Besides the elucidation of the artemisinin biosynthetic pathway, huge progress has been made in dissecting the complicated regulatory networks of artemisinin biosynthesis at the transcriptional and post-translational levels. Many transcription factors, which mediate different signaling pathways from plant hormones and other environmental factors like light, coldness etc, are involved in the regulation of artemisinin biosynthesis. To date, a variety of regulatory genes, such as those encoding transcription factors and kinases, have been characterized to play important parts in regulating artemisinin biosynthesis. These identified regulatory genes are valuable in developing A. annua plant lines with high-yield artemisinin and certain beneficial horticultural traits. In a recently published review, Zheng et al. made a comprehensive description of transcriptional regulatory network of artemisinin biosynthesis induced by diverse phytohormones and environmental factors, which would be helpful for better understanding the regulatory mechanism of artemisinin biosynthesis[25].
Moreover, as artemisinin is exclusively synthesized and stored in glandular trichomes (GT) of A. annua[23, 24], the density and number of GTs has a large effect on the content of artemisinin in A. annua plants. Therefore, it is also necessary to dissect the regulatory mechanism of glandular trichome formation and identify the regulatory factors involved.
In this review, we summarize the accomplishments in the study of the molecular regulation of artemisinin biosynthetic pathway and glandular trichome initiation, and also discuss biotechnological approaches toward higher artemisinin production in A. annua plants.
-
Plant hormones, like jasmonate (JA), abscisic acid (ABA), salicylic acid (SA) etc, and other environmental signals regulate artemisinin biosynthesis via the mediation of transcription factors (TF), and they form a cascade signaling network. Among the hormones, jasmonate (JA) signaling is most extensively studied. A number of transcription factors, which are responsive to these signals, have been identified to be involved in regulating artemisinin biosynthesis. These transcription factors belong to different TF families respectively, such as APETALA2/ethylene-response factors (AP2/ERF), WRKY, basic helix-loop-helix (bHLH), NAC and so on (Fig. 1).
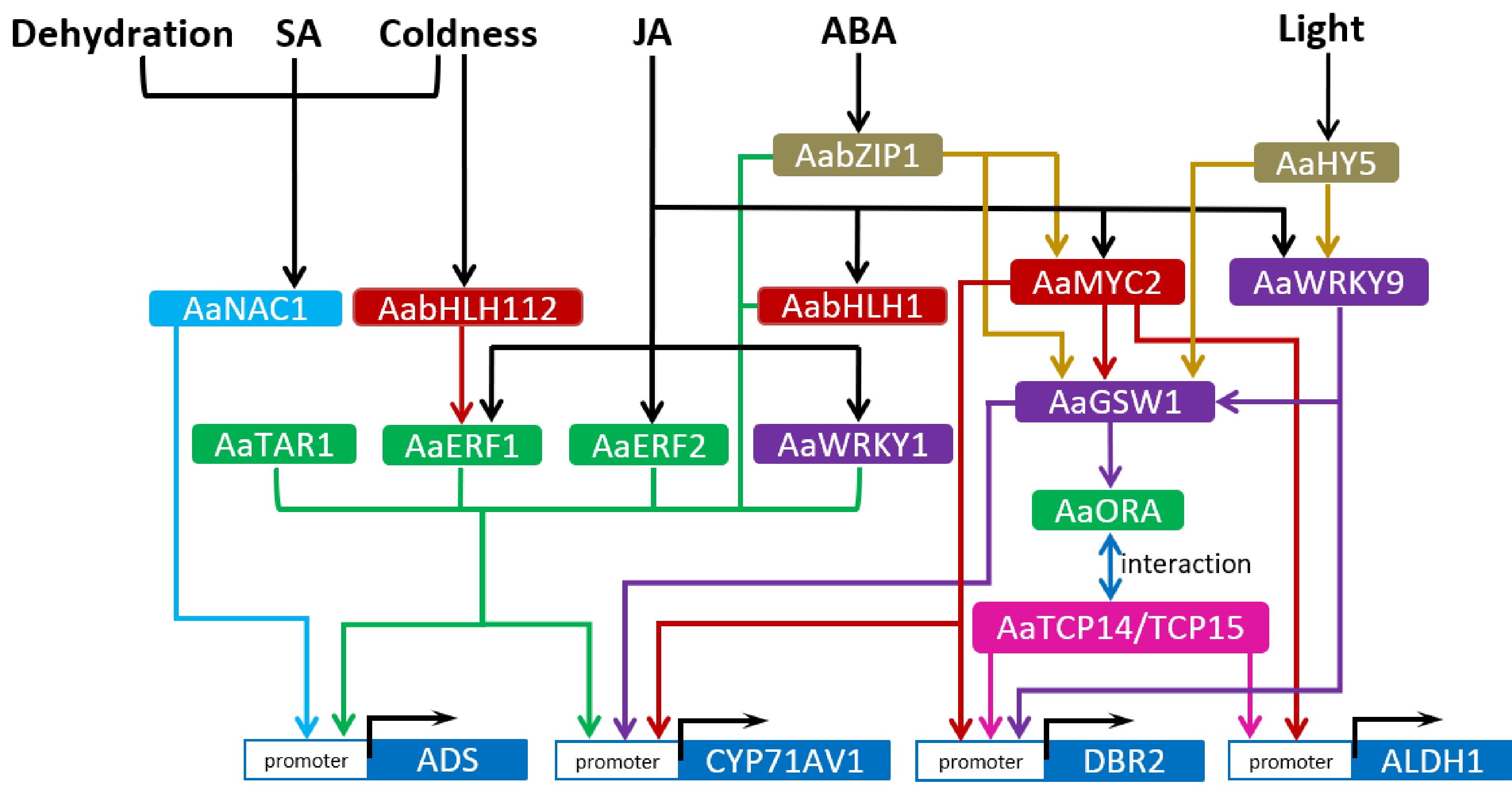
Figure 1.
Regulatory network of artemisinin biosynthetic pathway. The arrows represent direct upregulation of downstream targets. Arrows started from the common upstream regulators or directed toward the common downstream targets are in one colour. Transcription factors of the same family are marked with the same colour.
The AP2/ERF transcription factors
-
The APETALA2/Ethylene-Responsive Factors (AP2/ERFs) are one of the most important TF families that participate in stress response, developmental process and the regulation of secondary metabolism[26]. Some of them have been reported to regulate the biosynthesis of secondary metabolites, such as ORCA3 regulating the biosynthesis of monoterpenoid indole alkaloids (MIAs) in Catharanthus roseus[27] and NtERF32 regulating nicotine biosynthesis in tobacco[28]. In Artemisia annua, four AP2/ERF TFs (AaERF1, AaERF2, AaORA and AaTAR1) have been sequentially reported to be involved in regulating artemisinin biosynthesis[29−31]. Three of them, including AaERF1, AaERF2 and AaORA, are markedly induced by JA. AaERF1, AaERF2 and AaTAR1 are capable to bind to the CBF2 and RAA motifs in ADS and CYP71AV1 promoters, and activate the two genes’ expression[29, 31]. Besides, the trichome morphology/shape and cuticle composition are also regulated by AaTAR1 in A. annua[31]. AaORA is specifically expressed in the glandular and non-glandular T-shaped trichomes of A. annua, and positively regulates artemisinin biosynthesis and resistance to the fungal pathogen Botrytis cinerea[30]. However, AaORA was found not to directly bind to the promoters of the four artemisinin biosynthetic genes; rather, it interacts with AaTCP14 or AaTCP15, two Teosinte branched1/Cycloidea/Proliferating Cell Factors, to form a complex and enhance the transactivation activity of the two TCPs on their target genes such as DBR2 or ALDH1[32, 33], thereby promoting artemisinin biosynthesis.
WRKY transcription factors
-
WRKY transcription factors (TFs) make up a large family specific to plant species. WRKY TFs, with a conserved WRKY domain, regulate target genes’ expression through directly binding to their cis-elements called W-box[34]. AaWRKY1 is the first reported TF controlling artemisinin biosynthesis in A. annua[35]. AaWRKY1, highly expressed in GTs and induced by JA, could bind to the W-box of ADS and CYP71AV1 promoters and activate their expression[35, 36]. Then another WRKY TF, namely GLANDULAR TRICHOME-SPECIFIC WRKY 1 (AaGSW1), was identified to activate the expression of CYP71AV1 and AaORA by binding to their promoters, thus upregulating artemisinin biosynthesis[37]. AaGSW1 is responsive to both JA and ABA signals, and can be transactivated by AaMYC2 (a JA-responsive bHLH TF) and AabZIP1 (an ABA-responsive bZIP TF). Therefore, AaGSW1 integrates JA and ABA signaling pathways to regulate artemisinin biosynthesis. Furthermore, a recently reported AaWRKY9, which integrates JA and light signals, positively regulates artemisinin biosynthesis by activating the expression of AaGSW1 and DBR2[38]. Hence WRKY TFs are widely involved in mediating the regulation of artemisinin biosynthesis by diverse signals.
bHLH transcription factors
-
The basic helix-loop-helix (bHLH) TFs play an important part in the regulation of growth and development, secondary metabolism, stress response in plants[39−41]. So far many bHLH TFs have been functionally identified. AabHLH1, identified from A. annua, is responsive to JA and transactivates ADS and CYP71AV1 through binding to the E-box cis-elements in their promoters[42]. MYC2, another member of the bHLH family, plays a crucial role in regulating terpene biosynthesis in plants[43]. In A. annua, AaMYC2 is induced by JA and upregulates the expression of CYP71AV1, DBR2 and ALDH1 by binding to the G-box in their promoters[44, 45]. AaMYC2 could also directly activate AaGSW1 expression. At the post-translational level, the JASMONATE ZIM-DOMAIN (JAZ) proteins in JA signaling pathway and DELLA proteins in gibberellin signaling pathway could interact with AaMYC2, probably suppressing its transactivating function. Transgenic results indicated that AaMYC2 upregulated the biosynthesis of artemisinin and anthocyanins in A. annua plants[44]. Besides, AabHLH112, highly expressed in glandular trichomes of A. annua, is induced by coldness and upregulates the expression of AaERF1 by binding to its promoter, thus promoting artemisinin biosynthesis[46].
Other transcription factors
-
The NAC transcription factors are of a large plant-specific family that regulate stress response and cell development[47−49]. In A. annua, a NAC TF, AaNAC1, was identified to promote artemisinin production by enhancing ADS expression, as well as to enhance drought tolerance and resistance to Botrytis cinerea[50]. AaNAC1 can be induced by SA, JA, dehydration and coldness respectively, suggesting that this transcription factor may integrate diverse signaling pathways[50]. Moreover, AabZIP1, a transcription factor of basic leucine zipper (bZIP) family, is responsive to ABA signals and upregulates artemisinin biosynthesis through directly activating the expression of ADS, CYP71AV1 and AaMYC2[45, 51]. In addition, ETHYLENE-INSENSITIVE 3 (EIN3), a key TF involved in ethylene signaling, was found to negatively regulate the expression of artemisinin biosynthetic genes. Therefore, AaEIN3 is a negative regulator of artemisinin biosynthesis[52]. HY5, a key TF in light signaling, was found to transactivate AaWRKY9 and AaGSW1, thereby upregulating artemisinin biosynthesis[53]. These findings indicate that artemisinin biosynthesis can be regulated by diverse transcription factors that mediate diverse signaling pathways.
-
Artemisinin is specifically synthesized and stored in glandular secretory trichomes (GT) composed of 10 cells, due to GT-specific expression of artemisinin biosynthetic genes[23, 24]. The amount of GT has a determinative effect on the content of artemisinin in A. annua plants. So it is important to reveal the regulatory mechanism of glandular trichome formation, which would provide candidate regulatory factors valuable for increasing GT formation and elevating artemisinin production. So far, the identified regulatory factors involved in regulating GT formation in A. annua are mainly homeodomain-leucine zipper (HD-ZIP) IV and R2R3-MYB TFs (Fig. 2).
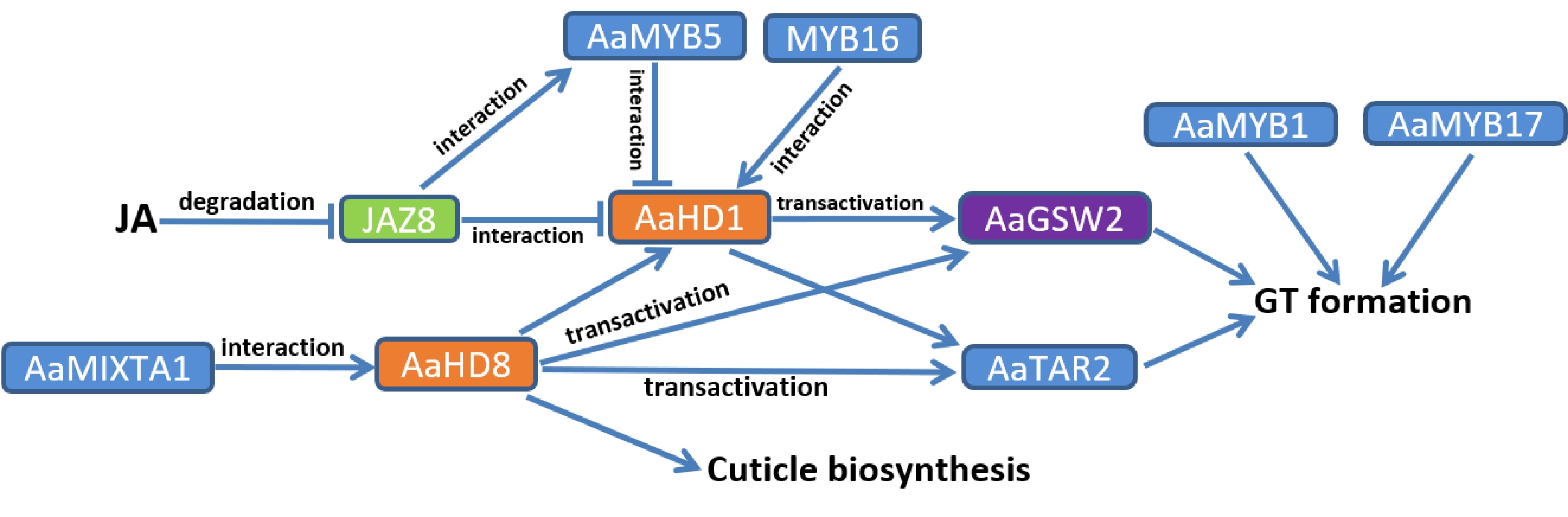
Figure 2.
Identified regulation of glandular trichome (GT) formation in A. annua. The arrows represent upregulation of downstream targets, while short lines represent inhibition or downregulation of downstream targets. Transcription factors of the same family are marked with the same colour.
HD-ZIP transcription factors
-
Homeodomain-leucine zipper (HD-ZIP) TFs, especially the IV (HD-ZIP IV) subfamily, were reported to regulate trichome development in plants[54, 55]. Two HD-ZIP IV transcription factors, AaHD1 and AaHD8, were sequentially identified to be positive regulators of trichome formation in A. annua. The JA-responsive AaHD1, specifically expressed in the basal cells of glandular and non-glandular trichomes of young A. annua leaves, positively regulates trichome formation through activating the expression of AaGSW2, a GT-specific WRKY TF that promotes GT initiation[56, 57]. Biochemical assays demonstrated that AaJAZ8 physically interacted with AaHD1 and suppressed its transactivating function[56]. AaHD8, highly expressed in trichomes, could bind to the L1-box of AaHD1 promoter and activate its expression; besides, it can activate the expression of cuticle biosynthesis genes[58]. AaMIXTA1 (a R2R3 MYB TF) interacted with AaHD8 and enhanced the function of AaHD8 in transactivating AaHD1 and cuticle biosynthesis genes[59]. These findings reflect the complicated associations between cuticle biosynthesis and trichome formation.
R2R3 MYB transcription factors
-
As the largest TF family in plants, the myeloblastosis (MYB) proteins regulate trichome development, root hair density, secondary metabolism, and stress response[60−63]. Among the MYB family, the R2R3 MYB TFs are of the largest subfamily, which contain two MYB domain repeats[64, 65]. Some R2R3 MYB TFs, including AaMYB1, AaMIXTA1, AaTAR2, AaMYB17, were sequentially identified to positively regulate glandular trichome formation, thereby elevating artemisinin content in A. annua[59, 63, 66, 67]. Overexpression of AaMYB1 led to an increase in the trichome density, probably by affecting gibberellin metabolism[63]. AaMIXTA1, mainly expressed in the GT basal cells of A. annua, positively regulated trichome initiation and cuticles biosynthesis through interacting with AaHD8 to strengthen its transactivation function[59]. AaTAR2 is mainly expressed in glandular and non-glandular trichome cells. Both AaHD1 and AaHD8 were found to be able to promote the expression of AaTAR2 by binding to its promoter[66]. Besides, two R2R3 MYB factors, AaMYB5 and AaMYB16, were reported to competitively interact with AaHD1 and affect its transactivation function on AaGSW2 promoter, thereby regulating GT initiation in A. annua[68]. AaMYB16 enhanced the transactivation function of AaHD1, while AaMYB5 weakened this function. Therefore, AaMYB16 is a positive regulator of GT initiation, while AaMYB5 is a negative regulator of GT formation[68]. These results show that the MYB proteins get involved in regulating GT initiation not only at the transcriptional level, but also at the post-translational level.
-
The elucidation of the artemisinin biosynthetic pathway as well as its regulatory network provided theoretical basis and potentially useful genes for engineering artemisinin production in A. annua. Based on these discoveries, several strategies are designed for promoting artemisinin production in A. annua, including: (1) overexpressing key enzymes in biosynthesis pathway, (2) repressing the competitive metabolic branch pathway, (3) making use of transcription factors (to regulate the biosynthetic pathway), and (4) increasing the glandular trichome density.
Engineering artemisinin biosynthetic pathway in A. annua
-
Generally, the common strategy for enhancing artemisinin production in A. annua is to overexpress rate-limiting enzymes in the biosynthetic pathway to break through the committed steps, in order for more metabolic flux to flow toward artemisinin biosynthesis. The cytosolic MVA pathway and the plastidial MEP pathway provide 5-carbon precursors (IPP and DMAPP) for artemisinin biosynthesis. HMGR is the rate-limiting enzyme in MVA pathway. When HMGR gene from Catharanthus roseus was overexpressed in A. annua, the transgenic lines displayed an increase of 22.5%–38.9% in artemisinin content, compared with wild-type plants[69, 70]. DXR is the rate-limiting enzyme in the MEP pathway, and overexpression of DXR caused a maximum of 1.3 fold increase of artemisinin content in A. annua[71]. Besides, overexpression of FPS, which catalyzes the condensation of IPPs to form FDP, led to a maximum of 1.5 fold increase in artemisinin level in A. annua[72, 73].
ADS is the first key enzyme in the artemisinin specific biosynthetic pathway. The content of artemisinin was increased by about 82% in ADS-overexpressing transgenic A. annua lines, compared to that in wild type plants[74]. Likewise, the genes of CYP71AV1 and its redox partner CPR were co-overexpressed in A. annua, and artemisinin content in transgenic lines was about 38% higher than that in the controls[71, 75].
Overexpressing a single pathway gene can enhance artemisinin accumulation only to a limited extent. Co-overexpression of two or more key enzyme genes in artemisinin biosynthetic pathway would be more effective to elevate artemisinin production. For example, co-overexpression of HMGR and ADS led to a maximum of 7.65 fold higher artemisinin content in transgenic A. annua lines than in the control lines[76]. Transgenic A. annua plants overexpressing the combination of FPS, CYP71AV1 and CPR had the artemisinin level 2.6 fold higher than that of the control plants[77]. In addition, co-overexpressing ADS, CYP71AV1 and CPR genes caused a maximum of 2.4 fold increase in artemisinin content in transgenic A. annua, compared to the control plants[78]. Meanwhile, co-overexpression of four genes including ADS, CYP71AV1, CPR and ALDH1 in A. annua caused an increase of artemisinin content by 2.4 fold at the most[79]. Exceptionally, co-overexpression of HMGR and FPS, which increased artemisinin level merely by 80% relative to the control[80], did not bring about a more significant elevation in artemisinin content compared with the single-gene (HMGR or FPS) overexpression in A. annua plants (Table 1). More combinations of target genes could be tried in the future for metabolic engineering of artemisinin production, and these combinations should be well evaluated and compared to identify the optimal one that can most effectively enhance artemisinin biosynthesis.
Table 1. Summary of genes used for metabolic engineering of artemisinin in A. annua.
Strategies for metabolic engineering of artemisinin Target genes used Artemisinin increment relative to control References Overexpressing key enzymes in artemisinin biosynthesis HMGR 22.5%−38.9% [69, 70] DXR 1.3 fold [71] FPS 1.5 fold [72, 73] ADS 82% [74] CYP71AV1/CPR 38% [71, 75] HMGR + FPS 80% [80] HMGR + ADS 7.65 fold [76] ADS + CYP71AV1/CPR 2.4 fold [78] FPS + CYP71AV1/CPR 2.6 fold [77] ADS + CYP71AV1/CPR+ ALDH1 2.4 fold [79] Repressing competitive pathways SQS 71% [82] CPS 77% [82] BFS 77% [82] GAS 1.03 fold [82] Overexpressing transcription factors AaERF1 68% [29] AaERF2 50% [29] AaORA 53% [30] AaTAR1 38% [31] AaTCP14 Nearly 1 fold [32] AaTCP15 Nearly 1 fold [33] AaTCP14+AaORA 1.8 fold [32] AaWRKY1 1.3-2 fold [36] AaGSW1 0.5-1 fold [37] AaWRKY9 0.6-1.2 fold [38] AaMYC2 23%−55% [44] AabHLH112 48%−70% [46] AaNAC1 46%−79% [50] AaEIN3(repression) About 35% [52] AabZIP1 0.7-1.5 fold [51] AaHY5 Nearly 1 fold [53] Increasing glandular trichome density AaHD1 50% [56] AaHD8 35% [58] AaMIXTA1 1 fold [59] AaMYB1 1 fold [63] AaTAR2 50% [66] AaMYB17 87% [67] AaMYB5(knockdown) 45%−84% [68] AaMYB16 43%−56% [68] AaGSW2 1 fold [57] Repressing the competitive metabolic branches
-
Farnesyl diphosphate (FDP) acts as a common precursor for the biosynthesis of artemisinin and other sesquiterpenes like β-farnesene, β-caryophyllene, squalene and so on[14, 81]. These diverse metabolic pathways are in competition for the same precursor. Repressing other sesquiterpenes' biosynthetic pathways would conduce to more metabolic flux into artemisinin biosynthetic pathway. For example, squalene synthase (SQS) is the key enzyme converting FDP into squalene, an intermediate in sterol biosynthesis[14]. Suppressing SQS expression by antisense technology in A. annua increased artemisinin biosynthesis by 71%. Repressing the expression of β-caryophyllene synthase (CPS), an enzyme converting FDP into β-caryophyllene, led to a 77% increase of artemisinin content in A. annua[82]. Likewise, repression of β-farnesene synthase (BFS), which converts FDP into β-farnesene, caused the artemisinin content to increase by 77% in A. annua. And repression of germacrene A synthase (GAS), an enzyme converting FDP into germacrene A, caused the artemisinin content to increase by 103%[82] (Table 1).
Overexpressing transcription factors
-
Transcription factors can usually regulate the expression of multiple genes in a certain pathway, and overexpression of these factors has been proposed as a promising way for efficiently upregulating a target metabolic pathway. At present, many transcription factors of different families have been identified to positively regulate artemisinin biosynthesis, which are potentially useful for engineering artemisinin production. For example, overexpression of AaORA in A. annua led to a maximum of 53% increase in artemisinin level, compared to wild type plants[30]; overexpressing AaMYC2 in A. annua increased artemisinin content by 23%–55% compared to the wild type[44]. The artemisinin level in AabHLH112-overexpression lines was 48%–70% higher than that in the control lines[46]. The artemisinin content in AabZIP1-overexpressing A. annua lines was increased by 0.7–1.5 fold compared with the wild-type[51]. In addition, transgenic lines overexpressing AaWRKY9 produced 0.6–1.2 fold more artemisinin than the control[38]. More examples of transcription factors overexpressed for elevating artemisinin yield are listed in Table 1.
Enhancing glandular trichome formation
-
Since artemisinin is exclusively synthesized and stored in glandular trichomes of A. annua, enhancing the formation of glandular trichomes would conduce to elevating artemisinin content in A. annua plants. Many regulatory factors related to glandular trichome formation have been identified, which are potentially useful for increasing glandular trichome density. For example, overexpression of AaHD1 in A. annua led to about 50% increase in glandular trichome density on mature leaves, with a concomitant increase of 50% in artemisinin content, compared to the control[56]. Overexpressing AaMYB17 in A. annua made the number of GTs on the adaxial leaf side increase by 30%–60% with a concomitant increase of artemisinin content, compared to the control[67]. The GT number on the leaf adaxial side in AaMIXTA1-overexpessing lines increased by approximately 50%, with the artemisinin content also rising by 1 fold, compared with that of the control[59]. Besides, overexpression of AaGSW2 in A. annua caused the GT density on the leaves to be double that of the wild type, with the artemisinin content also 2-fold that of wild-type controls[57]. More examples of regulatory factors used for increasing GT density are listed in Table 1.
-
Although artemisinin production by chemical synthesis or semi-synthesis in yeast has become successful, the A. annua plant remains the main commercial source of artemisinin. So it is of great importance to elevate artemisinin content in A. annua and develop new A. annua lines with high yield artemisinin by metabolic engineering and genetic breeding. To date, the artemisinin biosynthetic pathway has been completely elucidated, and many regulatory factors regulating artemisinin biosynthesis and glandular trichome formation have been identified. Many of these genes involved in artemisinin biosynthesis or its regulation have been used in the study for metabolic engineering of artemisinin production, and exhibited good potential for developing A. annua lines with high-yield artemisinin.
However, the complicated regulatory mechanism of artemisinin biosynthesis and GT initiation is still far from clear and requires further exploration. The majority of TFs identified to regulate artemisinin biosynthesis are related to JA signaling pathway. Those TFs involved in signaling pathways from other hormones like SA, ABA, ethylene, or environmental factors such as temperature, light, etc, have not been thoroughly characterized. Moreover, the presently identified regulators that regulate GT formation mostly lie upstream of the regulatory cascade pathways, and their targets downstream directly participating in the process of GT formation remain unknown. For example, what are the target genes downstream of AaGSW2? How do these genes function in the GT initiation process? The lack of such knowledge limits our comprehensive grasp of regulatory network of artemisinin biosynthesis and GT development. Elucidation of the above issues would provide more solid theoretical foundation for genetic engineering of artemisinin.
According to the present data, it appears that the single strategy adopted above for metabolic engineering have a relatively limited effect on the elevation of artemisinin content in A. annua. To further increase artemisinin production, the combination of multiple strategies could be tried, such as overexpressing multiple key enzyme genes in artemisinin biosynthetic pathway, combined with repressing competitive pathways and increasing the trichome number by genetic manipulation. Besides, it is also important to find out the optimal environmental parameters (such as light, temperature and humidity conditions) that are most suitable for A. annua growth. To conclude, more in-depth study is required to ultimately solve the shortage of artemisinin.
-
Zhihua Liao is the Editorial Board member of journal Medicinal Plant Biology. He was blinded from reviewing or making decisions on the manuscript. The article was subject to the journal's standard procedures, with peer-review handled independently of this Editorial Board member and his research groups.
- Copyright: © 2023 by the author(s). Published by Maximum Academic Press, Fayetteville, GA. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
-
About this article
Cite this article
Tang Y, Xiang L, Zhang F, Tang K, Liao Z. 2023. Metabolic regulation and engineering of artemisinin biosynthesis in A. annua. Medicinal Plant Biology 2:4 doi: 10.48130/MPB-2023-0004
Metabolic regulation and engineering of artemisinin biosynthesis in A. annua
- Received: 04 December 2022
- Accepted: 04 April 2023
- Published online: 08 May 2023
Abstract: Artemisinin is a potent anti-malarial sesquiterpene lactone that is naturally biosynthesized in glandular trichomes of a Chinese herbal plant, Artemisia annua. Although semi-synthesis of artemisinin in yeast has been feasible, at present the A. annua plant is still the main commercial source of artemisinin. The content of artemisinin however is low in A. annua, limiting its supply to malarial victims. So it's crucial to elevate artemisinin production in A. annua. Up to date artemisinin biosynthetic pathway has been completely elucidated. And many regulatory factors, mediating diverse plant hormone or environmental signaling routes, have been identified to get involved in the regulation of artemisinin biosynthesis and glandular trichome formation. Understanding the regulatory mechanisms of artemisinin biosynthesis and glandular trichome formation will be conducive to our practice for improving artemisinin production by metabolic engineering. In this review, the metabolic regulatory network with regard to artemisinin biosynthesis and glandular trichome formation is summarized, and the advance on metabolic engineering to increase artemisinin content in A. annua is also discussed.
-
Key words:
- Metabolic /
- Regulations /
- Engineering /
- Artemisinin












