Search
Submit Manuscript
Advanced Search
MAP  >  Circular Agricultural Systems
2024 Volume 4
Article Contents
Abstract
Introduction
Materials and methods
Plant materials
Chemicals and reagents
Preparation of Marselan juices and wines
Total polyphenols and flavonoid content determination
ABTS free-radical scavenging assay
FRAP free-radical scavenging assay
HS-GC-IMS analysis
Statistical data analysis
Results
Changes in total polyphenol and flavonoid contents and antioxidant activity during fermentation
Analysis of the change in volatile organic compounds (VOCs) during fermentation by GS-IMS
Fingerprint analysis of VOCs at different fermentation stages of Marselan wine
Multivariate statistical analysis
Conclusions
Author contributions
Data availability
Acknowledgments
Conflict of interest
Rights and permissions
References
About this article
Next Previous
ARTICLE   Open Access    

Optimizing the transplanting window for higher productivity of short and medium duration rice cultivars in Punjab, India using CERES-Rice model

  • Department of Climate Change and Agricultural Meteorology, Punjab Agricultural University, Ludhiana-141004, India

More Information
  • The CERES-Rice (V4.7.5) model was used to identify the optimum transplanting window for higher productivity of rice in Indian Punjab. The model was first sensitized for 11 genetic coefficients and then these values were used for calibrating and validating the model for rice cultivars. The Normalized Root Mean Square Error was in excellent range (< 10%) for all the parameters—the coefficient of determination (R2) for CVS. PR126 and PR127 for days taken to anthesis and maturity were 0.94 and 0.89−0.96, respectively while grain yield and LAI (leaf area index) were 0.89−0.98 and 0.87−0.89, respectively. The optimum transplanting window of 24−30 June for PR126 and 20−26 June for PR127 simulated the grain yield/LAI ranging from 8,425−8,473 kg·ha−1/4.23−4.24 for PR126 and 8,298−8,356 kg·ha−1/4.20−4.21 for PR127. The early transplantation of rice cultivars on 7th June resulted in the lowest yield/ LAI of 6,702 kg·ha−1/3.8 for PR126 and 6,865 kg·ha−1/3.9 for PR127. The deviation for the grain yield and HI (harvest index) of PR126 was between −14.2% to +8.2% and −15.1% to +10.5%, respectively, and of PR127 varied between −11.2% to +8.1% and −14.2% to +10.6%, respectively. The decline in the yield/HI from the average was observed during early transplantation in 2nd week of June (before the 15th of June for PR126 and the 13th of June for PR127) as well as late transplantation in the 1st week of July (after 11th July for PR126 and 6th July for PR127) for rice cultivars. The negative effect on yield and HI of both varieties during early and late transplantation could be due to unfavorable climatic conditions.

  • Introduction

    Starting in the early 2000s, China has experienced rapid growth as an emerging wine market. It has now established itself as the world's second-largest grape-growing country in terms of vineyard surface area. Furthermore, China has also secured its position as the sixth-biggest wine producer globally and the fifth-most significant wine consumer in terms of volume[1]. The Ningxia Hui autonomous region, known for its reputation as the highest quality wine-producing area in China, is considered one of the country's most promising wine regions. The region's arid or semiarid climate, combined with ample sunlight and warmth, thanks to the Yellow River, provides ideal conditions for grape cultivation. Wineries in the Ningxia Hui autonomous region are renowned as the foremost representatives of elite Chinese wineries. All wines produced in this region originate from grapes grown in their vineyards, adhering to strict quality requirements, and have gained a well-deserved international reputation for excellence. Notably, in 2011, Helan Mountain's East Foothill in the Ningxia Hui Autonomous Region received protected geographic indication status in China. Subsequently, in 2012, it became the first provincial wine region in China to be accepted as an official observer by the International Organisation of Vine and Wine (OIV)[2]. The wine produced in the Helan Mountain East Region of Ningxia, China, is one of the first Agricultural and Food Geographical Indications. Starting in 2020, this wine will be protected in the European Union[3].

    Marselan, a hybrid variety of Cabernet Sauvignon and Grenache was introduced to China in 2001 by the French National Institute for Agricultural Research (INRA). Over the last 15 years, Marselan has spread widely across China, in contrast to its lesser cultivation in France. The wines produced from Marselan grapes possess a strong and elegant structure, making them highly suitable for the preferences of Chinese consumers. As a result, many wineries in the Ningxia Hui Autonomous Region have made Marselan wines their main product[4]. Wine is a complex beverage that is influenced by various natural and anthropogenic factors throughout the wine-making process. These factors include soil, climate, agrochemicals, and human intervention. While there is an abundance of research available on wine production, limited research has been conducted specifically on local wines in the Eastern Foot of Helan Mountain. This research gap is of significant importance for the management and quality improvement of Chinese local wines.

    Ion mobility spectrometry (IMS) is a rapid analytical technique used to detect trace gases and characterize chemical ionic substances. It achieves this through the gas-phase separation of ionized molecules under an electric field at ambient pressure. In recent years, IMS has gained increasing popularity in the field of food-omics due to its numerous advantages. These advantages include ultra-high analytical speed, simplicity, easy operation, time efficiency, relatively low cost, and the absence of sample preparation steps. As a result, IMS is now being applied more frequently in various areas of food analysis, such as food composition and nutrition, food authentication, detection of food adulteration, food process control, and chemical food safety[5,6]. The orthogonal hyphenation of gas chromatography (GC) and IMS has greatly improved the resolution of complex food matrices when using GC-IMS, particularly in the analysis of wines[7].

    The objective of this study was to investigate the changes in the physicochemical properties of Marselan wine during the winemaking process, with a focus on the total phenolic and flavonoids content, antioxidant activity, and volatile profile using the GC-IMS method. The findings of this research are anticipated to make a valuable contribution to the theoretical framework for evaluating the authenticity and characterizing Ningxia Marselan wine. Moreover, it is expected that these results will aid in the formulation of regulations and legislation pertaining to Ningxia Marselan wine in China.

    Materials and methods

    Plant materials

    All the grapes used to produce Marselan wines, grow in the Xiban vineyard (106.31463° E and 38.509541° N) situated in Helan Mountain's East Foothill of Ningxia Hui Autonomous Region in China.

    Chemicals and reagents

    Folin-Ciocalteau reagent, (±)-6-Hydroxy-2,5,7,8-tetramethylchroman-2-carboxylic acid (Trolox), 2,20-azino-bis-(3-ethylbenzthiazoline-6-sulfonic acid) (ABTS), 2,4,6-tris (2-pyridyl)-s-triazine (TPTZ), anhydrous methanol, sodium nitrite, and sodium carbonate anhydrous were purchased from Shanghai Aladdin Biochemical Technology Co., Ltd. (Shanghai, China). Reference standards of (+)-catechin, gallic acid, and the internal standard (IS) 4-methyl-2-pentanol were supplied by Shanghai Yuanye Bio-Technology Co., Ltd (Shanghai, China). The purity of the above references was higher than 98%. Ultrapure water (18.2 MΩ cm) was prepared by a Milli-Q system (Millipore, Bedford, MA, USA).

    Preparation of Marselan juices and wines

    Stage 1−Juice processing: Grapes at the fully mature stage are harvested and crushed, and potassium metabisulfite (5 mg/L of SO2) was evenly spread during the crushing process. The obtained must is transferred into stainless steel tanks. Stage 2−Alcoholic fermentation: Propagated Saccharomyces cerevisiae ES488 (Enartis, Italy) are added to the fresh must, and alcoholic fermentation takes place, after the process is finished, it is kept in the tanks for 7 d for traditional maceration to improve color properties and phenolics content. Stage 3−Malolactic fermentation: When the pomace is fully concentrated at the bottom of the tanks, the wine is transferred to another tank for separation from these residues. Oenococcus oeni VP41 (Lallemand Inc., France) is inoculated and malic acid begins to convert into lactic acid. Stage 4−Wine stabilization: After malolactic fermentation, potassium metabisulfite is re-added (35 mg/L of SO2), and then transferred to oak barrels for stabilization, this process usually takes 6-24 months. A total of four batches of samples during the production process of Marselan wine were collected in this study.

    Total polyphenols and flavonoid content determination

    Total polyphenols were determined on 0.5 mL diluted wine sample using the Folin-Ciocalteu method[8], using gallic acid as a reference compound, and expressed as milligrams of gallic acid equivalents per liter of wine. The total flavonoid content was measured on 0.05 mL of wine sample by a colorimetric method previously described[9]. Results are calculated from the calibration curve obtained with catechin, as milligrams of catechin equivalents per liter of wine.

    ABTS free-radical scavenging assay

    The antioxidative activity was determined using the ABTS·+ assay[10]. Briefly, the ABTS·+ radical was prepared from a mixture of 88 μL of potassium persulfate (140 mmol/L) with 5 mL of the ABTS·+ solution (7 mmol/L). The reaction was kept at room temperature under the absence of light for 16 h. Sixty μL samples were mixed with 3 mL of ABTS·+ solution with measured absorption of 0.700 ± 0.200 at 734 nm. After 6 min reaction, the absorbance of samples were measured with a spectrophotometer at 734 nm. Each sample was tested in triplicate. The data were expressed as mmol Trolox equivalent of antioxidative capacity per liter of the wine sample (mmol TE/L). Calibration curves, in the range 64.16−1,020.20 μmol TE/L, showed good linearity (R2 ≥ 0.99).

    FRAP free-radical scavenging assay

    The FRAP assay was conducted according to a previous study[11]. The FRAP reagent was freshly prepared and mixed with 10 mM/L TPTZ solution prepared in 20 mM/L FeCl3·6H2O solution, 40 mM/L HCl, and 300 mM/L acetate buffer (pH 3.6) (1:1:10; v:v:v). Ten ml of diluted sample was mixed with 1.8 ml of FRAP reagent and incubated at 37 °C for 30 min. The absorbance was determined at 593 nm and the results were reported as mM Fe (II) equivalent per liter of the wine sample. The samples were analyzed and calculated by a calibration curve of ferrous sulphate (0.15−2.00 mM/mL) for quantification.

    HS-GC-IMS analysis

    The volatile compounds were analyzed on a GC-IMS instrument (FlavourSpec, GAS, Dortmund, Germany) equipped with an autosampler (Hanon Auto SPE 100, Shandong, China) for headspace analysis. One mL of each wine was sampled in 20 mL headspace vials (CNW Technologies, Germany) with 20 μL of 4-methyl-2-pentanol (20 mg/L) ppm as internal standard, incubated at 60 °C and continuously shaken at 500 rpm for 10 min. One hundred μL of headspace sample was automatically loaded into the injector in splitless mode through a syringe heated to 65 °C. The analytes were separated on a MxtWAX capillary column (30 m × 0.53 mm, 1.0 μm) from Restek (Bellefonte, Pennsylvania, USA) at a constant temperature of 60 °C and then ionized in the IMS instrument (FlavourSpec®, Gesellschaft für Analytische Sensorsysteme mbH, Dortmund, Germany) at 45 °C. High purity nitrogen gas (99.999%) was used as the carrier gas at 150 mL/min, and drift gas at 2 ml/min for 0−2.0 min, then increased to 100 mL/min from 2.0 to 20 min, and kept at 100 mL/min for 10 min. Ketones C4−C9 (Sigma Aldrich, St. Louis, MO, USA) were used as an external standard to determine the retention index (RI) of volatile compounds. Analyte identification was performed using a Laboratory Analytical Viewer (LAV) 2.2.1 (GAS, Dortmund, Germany) by comparing RI and the drift time of the standard in the GC-IMS Library.

    Statistical data analysis

    All samples were prepared in duplicate and tested at least six times, and the results were expressed as mean ± standard error (n = 4) and the level of statistical significance (p < 0.05) was analyzed by using Tukey's range test using SPSS 18.0 software (SPSS Inc., IL, USA). The principal component analysis (PCA) was performed using the LAV software in-built 'Dynamic PCA' plug-in to model patterns of aroma volatiles. Orthogonal partial least-square discriminant analysis (OPLS-DA) in SIMCA-P 14.1 software (Umetrics, Umeă, Sweden) was used to analyze the different volatile organic compounds in the different fermentation stages.

    Results

    Changes in total polyphenol and flavonoid contents and antioxidant activity during fermentation

    The results of the changes in the antioxidant activity of Marselan wines during the entire brewing process are listed in Table 1. It can be seen that the contents of flavonoids and polyphenols showed an increasing trend during the brewing process of Marselan wine, which range from 315.71−1,498 mg CE/L and 1,083.93−3,370.92 mg GAE/L, respectively. It was observed that the content increased rapidly in the alcoholic fermentation stage, but slowly in the subsequent fermentation stage. This indicated that the formation of flavonoid and phenolic substances in wine mainly concentrated in the alcoholic fermentation stage, which is consistent with previous reports. This is mainly because during the alcoholic fermentation of grapes, impregnation occurred to extract these compounds[12]. The antioxidant activities of Marselan wine samples at different fermentation stages were detected by FRAP and ABTS methods[11]. The results showed that the ferric reduction capacity and ABST·+ free radical scavenging capacity of the fermented Marselan wines were 2.4 and 1.5 times higher than the sample from the juice processing stage, respectively, indicating that the fermented Marselan wine had higher antioxidant activity. A large number of previous studies have suggested that there is a close correlation between antioxidant activity and the content of polyphenols and flavonoids[13−15]. Previous studies have reported that Marselan wine has the highest total phenol and anthocyanin content compared to the wine of Tannat, Cabernet Sauvignon, Merlot, Cabernet Franc, and Syrah[13]. Polyphenols and flavonoids play an important role in improving human immunity. Therefore, Marselan wines are popular because of their high phenolic and flavonoid content and high antioxidant capacity.

    Table 1.  GC-IMS integration parameters of volatile compounds in Marselan wine at different fermentation stages.
    No. Compounds Formula RI* Rt
    [sec]**    		 Dt
    [RIPrel]***    		 Identification
    approach    		 Concentration (μg/mL) (n = 4)
    Stage 1 Stage 2 Stage 3 Stage 4
    Aldehydes
    5 Furfural C5H4O2 1513.1 941.943 1.08702 RI, DT, IS 89.10 ± 4.05c 69.98 ± 3.22c 352.16 ± 39.06b 706.30 ± 58.22a
    6 Furfural dimer C5H4O2 1516.6 948.77 1.33299 RI, DT, IS 22.08 ± 0.69b 18.68 ± 2.59c 23.73 ± 2.69b 53.39 ± 9.42a
    12 (E)-2-hexenal C6H10O 1223.1 426.758 1.18076 RI, DT, IS 158.17 ± 7.26a 47.57 ± 2.51b 39.00 ± 2.06c 43.52 ± 4.63bc
    17 (E)-2-pentenal C5H8O 1129.2 333.392 1.1074 RI, DT, IS 23.00 ± 4.56a 16.42 ± 1.69c 18.82 ± 0.27b 18.81 ± 0.55b
    19 Heptanal C7H14O 1194.2 390.299 1.33002 RI, DT, IS 17.28 ± 2.25a 10.22 ± 0.59c 14.50 ± 8.84b 9.11 ± 1.06c
    22 Hexanal C6H12O 1094.6 304.324 1.25538 RI, DT, IS 803.11 ± 7.47c 1631.34 ± 19.63a 1511.11 ± 26.91b 1526.53 ± 8.12b
    23 Hexanal dimer C6H12O 1093.9 303.915 1.56442 RI, DT, IS 588.85 ± 7.96a 93.75 ± 4.67b 92.93 ± 3.13b 95.49 ± 2.50b
    29 3-Methylbutanal C5H10O 914.1 226.776 1.40351 RI, DT, IS 227.86 ± 6.39a 33.32 ± 2.59b 22.36 ± 1.18c 21.94 ± 1.73c
    33 Dimethyl sulfide C2H6S 797.1 193.431 0.95905 RI, DT, IS 120.07 ± 4.40c 87.a02 ± 3.82d 246.81 ± 5.62b 257.18 ± 3.04a
    49 2-Methylpropanal C4H8O 828.3 202.324 1.28294 RI, DT, IS 150.49 ± 7.13a 27.08 ± 1.48b 19.36 ± 1.10c 19.69 ± 0.92c
    Ketones
    45 3-Hydroxy-2-butanone C4H8O2 1293.5 515.501 1.20934 RI, DT, IS 33.20 ± 3.83c 97.93 ± 8.72b 163.20 ± 21.62a 143.51 ± 21.48a
    46 Acetone C3H6O 836.4 204.638 1.11191 RI, DT, IS 185.75 ± 8.16c 320.43 ± 12.32b 430.74 ± 3.98a 446.58 ± 10.41a
    Organic acid
    3 Acetic acid C2H4O2 1527.2 969.252 1.05013 RI, DT, IS 674.66 ± 46.30d 3602.39 ± 30.87c 4536.02 ± 138.86a 4092.30 ± 40.33b
    4 Acetic acid dimer C2H4O2 1527.2 969.252 1.15554 RI, DT, IS 45.25 ± 3.89c 312.16 ± 19.39b 625.79 ± 78.12a 538.35 ± 56.38a
    Alcohols
    8 1-Hexanol C6H14O 1365.1 653.825 1.32772 RI, DT, IS 1647.65 ± 28.94a 886.33 ± 32.96b 740.73 ± 44.25c 730.80 ± 21.58c
    9 1-Hexanol dimer C6H14O 1365.8 655.191 1.64044 RI, DT, IS 378.42 ± 20.44a 332.65 ± 25.76a 215.78 ± 21.04b 200.14 ± 28.34b
    13 3-Methyl-1-butanol C5H12O 1213.3 414.364 1.24294 RI, DT, IS 691.86 ± 9.95c 870.41 ± 22.63b 912.80 ± 23.94a 939.49 ± 12.44a
    14 3-Methyl-1-butanol dimer C5H12O 1213.3 414.364 1.49166 RI, DT, IS 439.90 ± 29.40c 8572.27 ± 60.56b 9083.14 ± 193.19a 9152.25 ± 137.80a
    15 1-Butanol C4H10O 1147.2 348.949 1.18073 RI, DT, IS 157.33 ± 9.44b 198.92 ± 3.92a 152.78 ± 10.85b 156.02 ± 9.80b
    16 1-Butanol dimer C4H10O 1146.8 348.54 1.38109 RI, DT, IS 24.14 ± 2.15c 274.75 ± 12.60a 183.02 ± 17.72b 176.80 ± 19.80b
    24 1-Propanol C3H8O 1040.9 274.803 1.11042 RI, DT, IS 173.73 ± 4.75a 55.84 ± 2.16c 80.80 ± 4.99b 83.57 ± 2.34b
    25 1-Propanol dimer C3H8O 1040.4 274.554 1.24784 RI, DT, IS 58.20 ± 1.30b 541.37 ± 11.94a 541.33 ± 15.57a 538.84 ± 9.74a
    28 Ethanol C2H6O 930.6 231.504 1.11901 RI, DT, IS 5337.84 ± 84.16c 11324.05 ± 66.18a 9910.20 ± 100.76b 9936.10 ± 101.24b
    34 Methanol CH4O 903.6 223.79 0.98374 RI, DT, IS 662.08 ± 13.87a 76.94 ± 2.15b 61.92 ± 1.96c 62.89 ± 0.81c
    37 2-Methyl-1-propanol C4H10O 1098.5 306.889 1.35839 RI, DT, IS 306.91 ± 4.09c 3478.35 ± 25.95a 3308.79 ± 61.75b 3313.85 ± 60.88b
    48 1-Pentanol C5H12O 1257.6 470.317 1.25222 RI, DT, IS 26.13 ± 2.52c 116.50 ± 3.71ab 112.37 ± 6.26b 124.17 ± 7.04a
    Esters
    1 Methyl salicylate C8H8O3 1859.6 1616.201 1.20489 RI, DT, IS 615.00 ± 66.68a 485.08 ± 31.30b 470.14 ± 23.02b 429.12 ± 33.74b
    7 Butyl hexanoate C10H20O2 1403.0 727.561 1.47354 RI, DT, IS 95.83 ± 17.04a 62.87 ± 3.62a 92.59 ± 11.88b 82.13 ± 3.61c
    10 Hexyl acetate C8H16O2 1298.6 524.366 1.40405 RI, DT, IS 44.72 ± 8.21a 33.18 ± 2.17d 41.50 ± 4.38c 40.89 ± 4.33b
    11 Propyl hexanoate C9H18O2 1280.9 499.577 1.39274 RI, DT, IS 34.65 ± 3.90d 70.43 ± 5.95a 43.97 ± 4.39b 40.12 ± 4.05c
    18 Ethyl hexanoate C8H16O2 1237.4 444.749 1.80014 RI, DT, IS 55.55 ± 5.62c 1606.16 ± 25.63a 787.24 ± 16.95b 788.91 ± 28.50b
    20 Isoamyl acetate C7H14O2 1127.8 332.164 1.30514 RI, DT, IS 164.22 ± 1.00d 243.69 ± 8.37c 343.51 ± 13.98b 365.46 ± 1.60a
    21 Isoamyl acetate dimer C7H14O2 1126.8 331.345 1.75038 RI, DT, IS 53.61 ± 4.79d 4072.20 ± 11.94a 2416.70 ± 49.84b 2360.46 ± 43.29c
    26 Isobutyl acetate C6H12O2 1020.5 263.605 1.23281 RI, DT, IS 101.65 ± 1.81a 15.52 ± 0.67c 44.87 ± 3.21b 45.96 ± 1.41b
    27 Isobutyl acetate dimer C6H12O2 1019.6 263.107 1.61607 RI, DT, IS 34.60 ± 1.05d 540.84 ± 5.64a 265.54 ± 8.31c 287.06 ± 3.66b
    30 Ethyl acetate dimer C4H8O2 885.2 218.564 1.33587 RI, DT, IS 1020.75 ± 6.86d 5432.71 ± 6.55a 5052.99 ± 9.65b 5084.47 ± 7.30c
    31 Ethyl acetate C4H8O2 878.3 216.574 1.09754 RI, DT, IS 215.65 ± 3.58a 38.29 ± 2.37c 71.59 ± 2.99b 69.32 ± 2.85b
    32 Ethyl formate C3H6O2 838.1 205.127 1.19738 RI, DT, IS 175.48 ± 3.79d 1603.20 ± 13.72a 1472.10 ± 5.95c 1509.08 ± 13.26b
    35 Ethyl octanoate C10H20O2 1467.0 852.127 1.47312 RI, DT, IS 198.86 ± 36.71b 1853.06 ± 17.60a 1555.51 ± 24.21a 1478.05 ± 33.63a
    36 Ethyl octanoate dimer C10H20O2 1467.0 852.127 2.03169 RI, DT, IS 135.50 ± 13.02d 503.63 ± 15.86a 342.89 ± 11.62b 297.28 ± 14.40c
    38 Ethyl butanoate C6H12O2 1042.1 275.479 1.5664 RI, DT, IS 21.29 ± 2.68c 1384.67 ± 8.97a 1236.52 ± 20.21b 1228.09 ± 5.09b
    39 Ethyl 3-methylbutanoate C7H14O2 1066.3 288.754 1.26081 RI, DT, IS 9.70 ± 1.85d 200.29 ± 4.21a 146.87 ± 8.70b 127.13 ± 12.54c
    40 Propyl acetate C5H10O2 984.7 246.908 1.48651 RI, DT, IS 4.57 ± 1.07c 128.63 ± 4.28a 87.75 ± 3.26b 88.49 ± 1.99b
    41 Ethyl propanoate C5H10O2 962.1 240.47 1.46051 RI, DT, IS 10.11 ± 0.34d 107.08 ± 3.50a 149.60 ± 5.39c 167.15 ± 12.90b
    42 Ethyl isobutyrate C6H12O2 971.7 243.229 1.56687 RI, DT, IS 18.29 ± 2.61d 55.22 ± 1.07c 98.81 ± 4.67b 104.71 ± 4.73a
    43 Ethyl lactate C5H10O3 1352.2 628.782 1.14736 RI, DT, IS 31.81 ± 2.91c 158.03 ± 2.80b 548.14 ± 74.21a 527.01 ± 39.06a
    44 Ethyl lactate dimer C5H10O3 1351.9 628.056 1.53618 RI, DT, IS 44.55 ± 2.03c 47.56 ± 4.02c 412.23 ± 50.96a 185.87 ± 31.25b
    47 Ethyl heptanoate C9H18O2 1339.7 604.482 1.40822 RI, DT, IS 39.55 ± 6.37a 38.52 ± 2.47a 28.44 ± 1.52c 30.77 ± 2.79b
    Unknown
    1 RI, DT, IS 15.53 ± 0.18 35.69 ± 0.80 12.70 ± 0.80 10.57 ± 0.86
    2 RI, DT, IS 36.71 ± 1.51 120.41 ± 3.44 198.12 ± 6.01 201.19 ± 3.70
    3 RI, DT, IS 44.35 ± 0.88 514.12 ± 4.28 224.78 ± 6.56 228.32 ± 4.62
    4 RI, DT, IS 857.64 ± 8.63 33.22 ± 1.99 35.05 ± 5.99 35.17 ± 3.97
    * Represents the retention index calculated using n-ketones C4−C9 as external standard on MAX-WAX column. ** Represents the retention time in the capillary GC column. *** Represents the migration time in the drift tube.
     | Show Table
    DownLoad: CSV

    Analysis of the change in volatile organic compounds (VOCs) during fermentation by GS-IMS

    This study adopted the GC-IMS method to test the volatile organic compounds (VOCs) in the samples from the different fermentation stages of Marselan wine. Figure 1 shows the gas phase ion migration spectrum obtained, in which the ordinate represents the retention time of the gas chromatographic peaks and the abscissa represents the ion migration time (normalized)[16]. The entire spectrum represents the aroma fingerprints of Marselan wine at different fermentation stages, with each signal point on the right of the relative reactant ion peak (RIP) representing a volatile organic compound detected from the sample[17]. Here, the sample in stage 1 (juice processing) was used as a reference and the characteristic peaks in the spectrum of samples in other fermentation stages were compared and analyzed after deducting the reference. The colors of the same component with the same concentration cancel each other to form a white background. In the topographic map of other fermentation stages, darker indicates higher concentration compared to the white background. In the 2D spectra of different fermentation stages, the position and number of peaks indicated that peak intensities are basically the same, and there is no obvious difference. However, it is known that fermentation is an extremely complex chemical process, and the content and types of volatile organic compounds change with the extension of fermentation time, so other detection and characterization methods are needed to make the distinction.

    Figure 1.  2D-topographic plots of volatile organic compounds in Marselan wine at different fermentation stages.
    DownLoad: Full-Size Img PowerPoint

    Fingerprint analysis of VOCs at different fermentation stages of Marselan wine

    To visually display the dynamic changes of various substances in the fermentation process of Marselan wine, peaks with obvious differences were extracted to form the characteristic fingerprints for comparison (Fig. 2). Each row represents all signal peaks selected from samples at the same stage, and each column means the signal peaks of the same volatile compound in samples from different fermentation stages. Figure 2 shows the volatile organic compounds (VOCs) information for each sample and the differences between samples, where the numbers represent the undetermined substances in the migration spectrum library. The changes of volatile substances in the process of Marselan winemaking is observed by the fingerprint. As shown in Fig. 2 and Table 2, a total of 40 volatile chemical components were detected by qualitative analysis according to their retention time and ion migration time in the HS-GC-IMS spectrum, including 17 esters, eight alcohols, eight aldehydes, two ketones, one organic acid, and four unanalyzed flavor substances. The 12 volatile organic compounds presented dimer due to ionization of the protonated neutral components before entering the drift tube[18]. As can be seen from Table 2, the VOCs in the winemaking process of Marselan wine are mainly composed of esters, alcohols, and aldehydes, which play an important role in the construction of aroma characteristics.

    Figure 2.  Fingerprints of volatile organic compounds in Marselan wine at different fermentation stages.
    DownLoad: Full-Size Img PowerPoint
    Table 2.  Antioxidant activity, total polyphenols, and flavonoids content of Marselan wine at different fermentation stages.
    Winemaking stage TFC (mg CE/L) TPC (mg GAE/L) FRAP (mM FeSO4/mL) ABTs (mM Trolox/L)
    Stage 1 315.71 ± 0.00d 1,083.93 ± 7.79d 34.82c 38.92 ± 2.12c
    Stage 2 1,490.00 ± 7.51c 3,225.51 ± 53.27c 77.32b 52.17 ± 0.95b
    Stage 3 1,510.00 ± 8.88a 3,307.143 ± 41.76b 77.56b 53.04 ± 0.76b
    Stage 4 1,498.57 ± 6.34b 3,370.92 ± 38.29a 85.07a 57.46 ± 2.55a
    Means in the same column with different letters are significantly different (p < 0.05).
     | Show Table
    DownLoad: CSV

    Esters are produced by the reaction of acids and alcohols in wine, mainly due to the activity of yeast during fermentation[19], and are the main components of fruit juices and wines that produce fruit flavors[20,21]. In this study, it was found that they were the largest detected volatile compound group in Marselan wine samples, which is consistent with previous reports[22]. It can be observed from Table 2 that the contents of most esters increased gradually with the extension of fermentation time, and they mainly began to accumulate in large quantities during the stage of alcohol fermentation. The contents of ethyl hexanoate (fruity), isoamyl acetate (banana, pear), ethyl octanoate (fruity, pineapple, apple, brandy), ethyl acetate (fruity), ethyl formate (spicy, pineapple), and ethyl butanoate (sweet, pineapple, banana, apple) significantly increased at the stage of alcoholic fermentation and maintained a high level in the subsequent fermentation stage (accounting for 86% of the total detected esters). These esters can endow a typical fruity aroma of Marselan wine, and played a positive role in the aroma profiles of Marselan wine. Among them, the content of ethyl acetate is the highest, which is 5,153.79 μg/mL in the final fermentation stage, accounting for 33.6% of the total ester. However, the content of ethyl acetate was relatively high before fermentation, which may be from the metabolic activity of autochthonous microorganisms present in the raw materials. Isobutyl acetate, ethyl 3-methyl butanoate, propyl acetate, ethyl propanoate, ethyl isobutyrate, and ethyl lactate were identified and quantified in all fermentation samples. The total contents of these esters in stage 1 and 4 were 255.28 and 1,533.38 μg/mL, respectively, indicating that they may also have a potential effect on the aroma quality of Marselan wine. The results indicate that esters are an important factor in the formation of flavor during the brewing process of Marselan wine.

    Alcohols were the second important aromatic compound in Marselan wine, which were mainly synthesized by glucose and amino acid decomposition during alcoholic fermentation[23,24]. According to Table 2, eight alcohols including methanol, ethanol, propanol, butanol, hexanol, amyl alcohol, 3-methyl-1-butanol, and 2-methyl-1-propanol were detected in the four brewing stages of Marselan wine. The contents of ethanol (slightly sweet), 3-methyl-1-butanol (apple, brandy, spicy), and 2-methyl-1-propanol (whiskey) increased gradually during the fermentation process. The sum of these alcohols account for 91%−92% of the total alcohol content, which is the highest content of three alcohols in Marselan wine, and may be contributing to the aromatic and clean-tasting wines. On the contrary, the contents of 1-hexanol and methanol decreased gradually in the process of fermentation. Notably, the content of these rapidly decreased at the stage of alcoholic fermentation, from 2,026.07 to 1,218.98 μg/mL and 662.08 to 76.94 μg/mL, respectively, which may be ascribed to volatiles changed from alcohols to esters throughout fermentation. The reduction of the concentration of some alcohols also alleviates the strong odor during wine fermentation, which plays an important role in the improvement of aroma characteristics.

    Acids are mainly produced by yeast and lactic acid bacteria metabolism at the fermentation stage and are considered to be an important part of the aroma of wine[22]. Only one type of acid (acetic acid) was detected in this experiment, which was less than previously reported, which may be related to different brewing processes. Acetic acid content is an important factor in the balance of aroma and taste of wine. Low contents of volatile acids can provide a mild acidic smell in wine, which is widely considered to be ideal for producing high-quality wines. However, levels above 700 μg/mL can produce a pungent odor and weaken the wine's distinctive flavor[25]. The content of acetic acid increased first and then decreased during the whole fermentation process. The content of acetic acid increased rapidly in the second stage, from 719.91 to 3,914.55 μg/mL reached a peak in the third stage (5,161.81 μg/mL), and decreased to 4,630.65 μg/mL in the last stage of fermentation. Excessive acetic acid in Marselan wine may have a negative impact on its aroma quality.

    It was also found that the composition and content of aldehydes produced mainly through the catabolism of amino acids or decarboxylation of ketoacid were constantly changing during the fermentation of Marselan wines. Eight aldehydes, including furfural, hexanal, heptanal, 2-methylpropanal, 3-methylbutanal, dimethyl sulfide, (E)-2-hexenal, and (E)-2-pentenal were identified in all stage samples. Among them, furfural (caramel bread flavor) and hexanal (grass flavor) are the main aldehydes in Marselan wine, and the content increases slightly with the winemaking process. While other aldehydes such as (E)-2-hexenal (green and fruity), 3-methylbutanol (fresh and malt), and 2-methylpropanal (fresh and malt) were decomposed during brewing, reducing the total content from 536.52 to 85.15 μg/mL, which might potently affect the final flavor of the wine. Only two ketones, acetone, and 3-hydroxy-2-butanone, were detected in the wine samples, and their contents had no significant difference in the fermentation process, which might not affect the flavor of the wine.

    Multivariate statistical analysis

    To more intuitively analyze the differences of volatile organic compounds in different brewing stages of Marselan wine samples, principal component analysis was performed[26−28]. As presented in Fig. 3, the points corresponding to one sample group were clustered closely on the score plot, while samples at different fermentation stages were well separated in the plot. PC1 (79%) and PC2 (18%) together explain 97% of the total variance between Marselan wine samples, indicating significant changes in volatile compounds during the brewing process. As can be seen from the results in Fig. 3, samples of stages 1, 2, and 3 can be distinguished directly by PCA, suggesting that there are significant differences in aroma components in these three fermentation stages. Nevertheless, the separation of stage 3 and stage 4 samples is not very obvious and both presented in the same quadrant, which means that their volatile characteristics were highly similar, indicating that the volatile components of Marselan wine are formed in stage 3 during fermentation (Fig. S1). The above results prove that the unique aroma fingerprints of the samples from the distinct brewing stages of Marselan wine were successfully constructed using the HS-GC-IMS method.

    Figure 3.  PCA based on the signal intensity obtained with different fermentation stages of Marselan wine.
    DownLoad: Full-Size Img PowerPoint

    Based on the results of the PCA, OPLS-DA was used to eliminate the influence of uncontrollable variables on the data through permutation test, and to quantify the differences between samples caused by characteristic flavors[28]. Figure 4 revealed that the point of flavor substances were colored according to their density and the samples obtained at different fermentation stages of wine have obvious regional characteristics and good spatial distribution. In addition, the reliability of the OPLS-DA model was verified by the permutation method of 'Y-scrambling'' validation. In this method, the values of the Y variable were randomly arranged 200 times to re-establish and analyze the OPLS-DA model. In general, the values of R2 (y) and Q2 were analyzed to assess the predictability and applicability of the model. The results of the reconstructed model illustrate that the slopes of R2 and Q2 regression lines were both greater than 0, and the intercept of the Q2 regression line was −0.535 which is less than 0 (Fig. 5). These results indicate that the OPLS-DA model is reliable and there is no fitting phenomenon, and this model can be used to distinguish the four brewing stages of Marselan wine.

    Figure 4.  Scores plot of OPLS-DA model of volatile components in Marselan wine at different fermentation stages.
    DownLoad: Full-Size Img PowerPoint
    Figure 5.  Permutation test of OPLS-DA model of volatile components in Marselan wine at different fermentation stages (n = 200).
    DownLoad: Full-Size Img PowerPoint

    VIP is the weight value of OPLS-DA model variables, which was used to measure the influence intensity and explanatory ability of accumulation difference of each component on classification and discrimination of each group of samples. In previous studies, VIP > 1 is usually used as a screening criterion for differential volatile substances[28−30]. In this study, a total of 22 volatile substances had VIP values above 1, indicating that these volatiles could function as indicators of Marselan wine maturity during fermentation (see Fig. 6). These volatile compounds included furfural, ethyl lactate, heptanal, dimethyl sulfide, 1-propanol, ethyl isobutyrate, propyl acetate, isobutyl acetate, ethanol, ethyl hexanoate, acetic acid, methanol, ethyl formate, ethyl 3-methylbutanoate, ethyl acetate, hexanal, isoamyl acetate, 2-methylpropanal, 2-methyl-1-propanol, and three unknown compounds.

    Figure 6.  VIP plot of OPLS-DA model of volatile components in Marselan wine at different fermentation stages.
    DownLoad: Full-Size Img PowerPoint

    Conclusions

    This study focuses on the change of volatile flavor compounds and antioxidant activity in Marselan wine during different brewing stages. A total of 40 volatile aroma compounds were identified and collected at different stages of Marselan winemaking. The contents of volatile aroma substances varied greatly at different stages, among which alcohols and esters were the main odors in the fermentation stage. The proportion of furfural was small, but it has a big influence on the wine flavor, which can be used as one of the standards to measure wine flavor. Flavonoids and phenols were not only factors of flavor formation, but also important factors to improve the antioxidant capacity of Marselan wine. In this study, the aroma of Marselan wines in different fermentation stages was analyzed, and its unique aroma fingerprint was established, which can provide accurate and scientific judgment for the control of the fermentation process endpoint, and has certain guiding significance for improving the quality of Marselan wines (Table S1). In addition, this work will provide a new approach for the production management of Ningxia's special wine as well as the development of the native Chinese wine industry.

  • The authors confirm contribution to the paper as follows: study conception and design: Gong X, Fang L; data collection: Fang L, Li Y; analysis and interpretation of results: Qi N, Chen T; draft manuscript preparation: Fang L. All authors reviewed the results and approved the final version of the manuscript.

  • The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

    • Acknowledgments

    This work were supported by the project of Hainan Province Science and Technology Special Fund (ZDYF2023XDNY031) and the Central Public-interest Scientific Institution Basal Research Fund for Chinese Academy of Tropical Agricultural Sciences in China (Grant No. 1630122022003).

  • The authors declare that they have no conflict of interest.

  • [1]

    Fukagawa NK, Ziska LH. 2019. Rice: importance for global nutrition. Journal of Nutritional Science and Vitaminology 65:S2−S3

    doi: 10.3177/jnsv.65.S2

    CrossRef   Google Scholar

    [2]

    United States Department of Agriculture (USDA), Foreign Agricultural Service. 2021. Livestock and poultry: world market and trade. https://fas.usda.gov/data/commodities/rice
    [3]

    Statista. 2022. Total area of cultivation for rice across India from financial year 2014 to 2020, with an estimate for 2021. www.statista.com/statistics/765691/india-area-of-cultivation-for-rice/#:~:text=At%20the%20end%20of%20fiscal,across%20the%20south%20Asian%20nation
    [4]

    Grover D, Singh JM, Kumar A, Kumar S. 2017. State Agricultural Profile - Punjab. pp. 1−74. http://dx.doi.org/10.13140/RG.2.2.29375.87203
    [5]

    Pathak H, Tripathi R, Jambhulkar NN, Bisen JP, Panda BB. 2020. Eco-regional rice farming for enhancing productivity, profitability and sustainability. NRRI Research Bull 22. ICAR-National Rice Research Institute, Cuttack, Odisha. pp 28.
    [6]

    Prabhjyot-Kaur, Sandhu SS, Dhillon BS, Singh H. 2021. Rice yield variability in Punjab – an overview of five decades. Paddy and Water Environment 19:673−81

    doi: 10.1007/s10333-021-00866-3

    CrossRef   Google Scholar

    [7]

    Anonymous. 2022. Package of practices for crops in Punjab (Kharif 2022). Centre for Communication and International Linkages, Punjab Agricultural University, Ludhiana, Punjab. www.pau.edu/content/ccil/pf/pp_kharif.pdf
    [8]

    Geng S, Hess CE, Auburn J. 1990. Sustainable agricultural systems: concepts and definitions. Journal of Agronomy and Crop Science 165:73−85

    doi: 10.1111/j.1439-037x.1990.tb00837.x

    CrossRef   Google Scholar

    [9]

    Chipanshi AC, Chanda R, Totolo O. 2003. Vulnerability assessment of the maize and Sorghum crops to climate change in Botswana. Climatic Change 61:339−60

    doi: 10.1023/B:CLIM.0000004551.55871.eb

    CrossRef   Google Scholar

    [10]

    Teng PPS, Caballero-Anthony M, Lassa JA. 2016. The future of rice security under climate change. Report. NTS Report No. 4. Centre for Non Traditional Security Studies(NTS), Singapore. www.rsis.edu.sg/wp-content/uploads/2016/10/NTS-Report4-July2016-ClimateChangeAndRice.Pdf
    [11]

    Satake T, Yoshida S. 1978. High temperature-induced sterility in indica rices at flowering. Japanese Journal of Crop Science 47:6−17

    doi: 10.1626/jcs.47.6

    CrossRef   Google Scholar

    [12]

    Gupta R, Mishra A. 2019. Climate change induced impact and uncertainty of rice yield of agro-ecological zones of India. Agricultural Systems 173:1−11

    doi: 10.1016/j.agsy.2019.01.009

    CrossRef   Google Scholar

    [13]

    Debnath S, Mishra A, Mailapalli DR, Raghuwanshi NS, Sridhar V. 2021. Assessment of rice yield gap under a changing climate in India. Journal of Water and Climate Change 12:1245−67

    doi: 10.2166/wcc.2020.086

    CrossRef   Google Scholar

    [14]

    Leakey ADB, Uribelarrea M, Ainsworth EA, Naidu SL, Rogers A, et al. 2006. Photosynthesis, productivity, and yield of maize are not affected by open-air elevation of CO2 concentration in the absence of drought. Plant Physiology 140:779−90

    doi: 10.1104/pp.105.073957

    CrossRef   Google Scholar

    [15]

    Hernández N, Soto F, Caballero A. 2009. Modelos de simulación de cultivos: Características y usos. Cultivos Tropicales 30(1):73−82

    Google Scholar

    [16]

    Jones JW, Antle JM, Basso B, Boote KJ, Conant RT, et al. 2017. Brief history of agricultural systems modeling. Agricultural Systems 155:240−54

    doi: 10.1016/j.agsy.2016.05.014

    CrossRef   Google Scholar

    [17]

    Jones JW, Hoogenboom G, Porter CH, Boote KJ, Batchelor WD, et al. 2003. The DSSAT cropping system model. European Journal of Agronomy 18:235−65

    doi: 10.1016/s1161-0301(02)00107-7

    CrossRef   Google Scholar

    [18]

    Thigpen J. 2018. Ongoing improvements and applications of the CERES-Rice model. https://agrilinks.org/post/ongoing-improvements-and-applications-ceres-rice-model
    [19]

    Xiong W, Balkovič J, van der Velde M, Zhang X, Izaurralde RC, et al. 2014. A calibration procedure to improve global rice yield simulations with EPIC. Ecological Modelling 273:128−39

    doi: 10.1016/j.ecolmodel.2013.10.026

    CrossRef   Google Scholar

    [20]

    Daggupati P, Pai N, Ale S, et al. 2015. A recommended calibration and validation strategy for hydrologic and water quality models. Transactions of the ASABE 58:1705−19

    doi: 10.13031/trans.58.10712

    CrossRef   Google Scholar

    [21]

    Ahmed M, Akram MN, Asim M, Aslam M, Hassan FU, et al. 2016. Calibration and validation of APSIM-Wheat and CERES-Wheat for spring wheat under rainfed conditions. Computers and Electronics in Agriculture 123:384−401

    doi: 10.1016/j.compag.2016.03.015

    CrossRef   Google Scholar

    [22]

    Prabhjyot-Kaur, Singh H, Hundal SS. 2018. Application of CERES- and GRO-models as a research and agronomic tool in irrigated plains of Punjab, India. Journal of Agricultural Physics 18(1):58−67

    Google Scholar

    [23]

    Vijayalaxmi G, Sreenivas G, Leela Rani P. 2016. Evaluation of CERES-rice model under various plant densities and age of seedlings in transplanted rice in southern Telangana zone of Telangana State, India. International Journal of Current Microbiology and Applied Sciences 5:667−74

    doi: 10.20546/ijcmas.2016.504.076

    CrossRef   Google Scholar

    [24]

    Chandrvavanshi R, Kar G, Upadhyay S, Kumar Sinha P, Rohit. 2019. Simulation of crop growth and productivity using simulation model for short duration rice. International Journal of Current Microbiology and Applied Sciences 8:2081−88

    doi: 10.20546/ijcmas.2019.812.246

    CrossRef   Google Scholar

    [25]

    Rajwade YA, Swain DK, Tiwari KN. 2018. Effect of irrigation method on adaptation capacity of rice to climate change in subtropical India. International Journal of Plant Production 12:203−17

    doi: 10.1007/s42106-018-0021-3

    CrossRef   Google Scholar

    [26]

    Monod H, Naud C, Makowski D. 2006. Uncertainty and sensitivity analysis for crop models. In Working with dynamic crop models: Evaluation, analysis, parameterization, and applications, eds. Wallach D, Makowski D, Jones JW, Brun F. 1st Edition. Amsterdam, The Netherlands: Elsevier. pp. 55−100.
    [27]

    Lamsal A, Anandhi A, Welch S. 2012. Modeling the uncertainty in responsiveness of climatic, genetic, soil and agronomic parameters in CERES-Sorghum model across locations in Kansas, USA. Abstract ID GC43D-1055. Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA.
    [28]

    Wilmott CJ. 1982. Some comments on the evaluation of model performance. Bulletin of the American Meteorological Society 63:1309−13

    doi: 10.1175/1520-0477(1982)063<1309:SCOTEO>2.0.CO;2

    CrossRef   Google Scholar

    [29]

    Jamieson PD, Porter JR, Wilson DR. 1991. A test of the computer simulation model ARCWHEAT1 on wheat crops grown in New Zealand. Field Crops Research 27:337−50

    doi: 10.1016/0378-4290(91)90040-3

    CrossRef   Google Scholar

    [30]

    Nash JE, Sutcliffe JV. 1970. River flow forecasting through conceptual models part I — a discussion of principles. Journal of Hydrology 10:282−90

    doi: 10.1016/0022-1694(70)90255-6

    CrossRef   Google Scholar

    [31]

    Ge H, Ma F, Li Z, Du C. 2021. Global sensitivity analysis for CERES-rice model under different cultivars and specific-stage variations of climate parameters. Agronomy 11:2446

    doi: 10.3390/agronomy11122446

    CrossRef   Google Scholar

    [32]

    Goswami P, Dutta G. 2020. Evaluation of DSSAT model (CERES rice) on rice production: a review. International Journal of Chemical Studies 8:404−9

    doi: 10.22271/chemi.2020.v8.i5f.10327

    CrossRef   Google Scholar

    [33]

    Mote BM, Kumar N. 2016. Calibration and validation of CERES-rice model for different rice cultivars at Navsari. Journal of Agrometeorology 18:155−57

    doi: 10.54386/jam.v18i1.924

    CrossRef   Google Scholar

    [34]

    Ray M, Roul PK, Baliarsingh A. 2018. Application of DSSAT crop simulation model to estimate rice yield in keonjhar district of Odisha (India) under changing climatic conditions. International Journal of Current Microbiology and Applied Sciences 7:659−67

    doi: 10.20546/ijcmas.2018.704.075

    CrossRef   Google Scholar

    [35]

    Jha RK, Kalita PK, Jat R. 2020. Development of production management strategies for a long-duration rice variety: Rajendra Mahsuri — using crop growth model, DSSAT, for the state of Bihar, India. Paddy and Water Environment 18:531−45

    doi: 10.1007/s10333-020-00799-3

    CrossRef   Google Scholar

    [36]

    Yang JY, Huffman ECT. 2004. EasyGrapher: software for graphical and statistical validation of DSSAT outputs. Computers and Electronics in Agriculture 45:125−32

    doi: 10.1016/j.compag.2004.06.006

    CrossRef   Google Scholar

    [37]

    Sandhu SS, Kaur P, Gill KK, Vashisth BB. 2020. The effect of recent climate shifts on optimal sowing windows for wheat in Punjab, India. Journal of Water and Climate Change 11:1177−90

    doi: 10.2166/wcc.2019.241

    CrossRef   Google Scholar

    [38]

    Kothiyal S, Prabhjyot-Kaur and Sandhu SS. 2021. Determination of sowing window for kharif maize in Punjab, India using sensitized, calibrated and validated CERES-Maize model. Maydica 66(3):1−12 https://journals-crea.4science.it/index.php/maydica/article/view/2397/1401
    [39]

    Brar SK, Mahal SS, Brar AS, Vashist KK, Sharma N, et al. 2012. Transplanting time and seedling age affect water productivity, rice yield and quality in north-west India. Agricultural Water Management 115:217−22

    doi: 10.1016/j.agwat.2012.09.001

    CrossRef   Google Scholar

    [40]

    Kushwaha U. 2018. Delayed transplanting causes the yield difference between experimental plot and farmer's field in rice in rice. Global Journal of Agricultural Research 6(1):9−17

    doi: 10.37745/gjar.2013

    CrossRef   Google Scholar

    [41]

    Singh PK, Singh KK, Bhan SC, Baxla AK, Singh S, et al. 2017. Impact of projected climate change on rice (Oryza sativa L. ) yield using CERES-rice model in different agroclimatic zones of India. Current Science 112:108

    doi: 10.18520/cs/v112/i01/108-115

    CrossRef   Google Scholar

    [42]

    Vishwakarma A, Singh JK, Sen A, Bohra JS, Singh S. 2016. Effect of transplanting date and age of seedlings on growth, yield and quality of hybrids under system of rice (Oryza sativa) intensification and their effect on soil fertility. The Indian Journal of Agricultural Sciences 86:679−85

    doi: 10.56093/ijas.v86i5.58355

    CrossRef   Google Scholar

    [43]

    Deka AM, Bora PC, Kalita H, Guha B, Thakuria K. 2019. Effect of dates and methods of rice (Oryza sativa) transplantation on growth and yield, nutrient uptake and economics of ricelentil (Lens culinaris) system. Indian Journal of Agronomy 64:310−14

    doi: 10.59797/ija.v64i3.5275

    CrossRef   Google Scholar

  • Cite this article

    Aryal A, Prabhjyot-Kaur, Sandhu SS, Kothiyal S. 2024. Optimizing the transplanting window for higher productivity of short and medium duration rice cultivars in Punjab, India using CERES-Rice model. Circular Agricultural Systems 4: e011 doi: 10.48130/cas-0024-0010
    Aryal A, Prabhjyot-Kaur, Sandhu SS, Kothiyal S. 2024. Optimizing the transplanting window for higher productivity of short and medium duration rice cultivars in Punjab, India using CERES-Rice model. Circular Agricultural Systems 4: e011 doi: 10.48130/cas-0024-0010
    shu

Figures(5)  /  Tables(4)

Download PDF

Article Metrics

Article views(2236) PDF downloads(436)

Other Articles By Authors

ARTICLE   Open Access    

Optimizing the transplanting window for higher productivity of short and medium duration rice cultivars in Punjab, India using CERES-Rice model

  • Department of Climate Change and Agricultural Meteorology, Punjab Agricultural University, Ludhiana-141004, India

  • Received: 09 November 2023
  • Revised: 04 March 2024
  • Accepted: 19 March 2024
  • Published online: 04 June 2024
Circular Agricultural Systems  4,  Article number: e011  (2024)  |  Cite this article

Abstract: The CERES-Rice (V4.7.5) model was used to identify the optimum transplanting window for higher productivity of rice in Indian Punjab. The model was first sensitized for 11 genetic coefficients and then these values were used for calibrating and validating the model for rice cultivars. The Normalized Root Mean Square Error was in excellent range (< 10%) for all the parameters—the coefficient of determination (R2) for CVS. PR126 and PR127 for days taken to anthesis and maturity were 0.94 and 0.89−0.96, respectively while grain yield and LAI (leaf area index) were 0.89−0.98 and 0.87−0.89, respectively. The optimum transplanting window of 24−30 June for PR126 and 20−26 June for PR127 simulated the grain yield/LAI ranging from 8,425−8,473 kg·ha−1/4.23−4.24 for PR126 and 8,298−8,356 kg·ha−1/4.20−4.21 for PR127. The early transplantation of rice cultivars on 7th June resulted in the lowest yield/ LAI of 6,702 kg·ha−1/3.8 for PR126 and 6,865 kg·ha−1/3.9 for PR127. The deviation for the grain yield and HI (harvest index) of PR126 was between −14.2% to +8.2% and −15.1% to +10.5%, respectively, and of PR127 varied between −11.2% to +8.1% and −14.2% to +10.6%, respectively. The decline in the yield/HI from the average was observed during early transplantation in 2nd week of June (before the 15th of June for PR126 and the 13th of June for PR127) as well as late transplantation in the 1st week of July (after 11th July for PR126 and 6th July for PR127) for rice cultivars. The negative effect on yield and HI of both varieties during early and late transplantation could be due to unfavorable climatic conditions.

    HTML

    Introduction

    • Rice (Oryza sativa) is the most important staple food and one of the oldest edible cereal crops in the world. Asia alone contributes 90% of total global production of rice[1]. According to the USDA[2], rice occupied 162.48 million hectares of area on a global basis during 2018−2019 and total production was approximately 500 million metric tonnes where India contributed nearly 24% of worldwide production. Rice is an important kharif crop of India which is grown over an area of approximately 45.0 million hectares[3]. Punjab is recognized as food crop granary of India for large scale intensive agricultural system[4] and it is the second largest state in the country in terms of rice production[5] and its cultivation has increased by 167.5% or at 3.5% per year during the period 1970 to 2017[6]. During 2020−2021, rice occupied approximately 32 lakh hectares area in Punjab[7]. Rice is grown extensively in the agro-climatic zones of undulating plains, the central plains and the eastern parts of the western zones in Punjab. A temperature range of 20 to 37.5 °C is favorable for its optimum growth and development. Loamy soils with low permeability having a pH range 5 to 9 are found to be the best for rice cultivation. Rice is a semi-aquatic crop whose growth is best facilitated under submerged conditions. Under transplanted conditions, it is recommended to sow rice seed in a nursery bed between 20th May and 5th June and transplantation is done after 25−30 d in case of short-duration varieties and 30−35 d for long-duration varieties[7]. Rice production is greatly affected by agronomic practices like selection of cultivar, planting density, transplanting date, fertilizer management, irrigation application, etc.[8]. Rice is the only crop to survive waterlogging in anaerobic conditions and one of the major cereal crops of the entire world. But global warming and climate change have put its production potential at major risk.

      Climate change, being the most important issue in the modern world, has placed biological and environmental subsistence at peril[9] by threatening food security. On the basis of CMIP5 models two major rice production hubs of India (Punjab and Uttar Pradesh) would witness a rise in mean temperature by 2 and 3 °C by 2050 and 2080, respectively[10]. Such an increase in mean temperature can have an adverse impact on rice production. In the case of rice, if temperatures rise above 35 °C at the flowering stage then spikelet sterility is induced and productivity is affected[11]. According to Gupta & Mishra[12] due to climate change, the yield of rice in India could vary in the 2020s, 2050s, and 2080s by 1.2%−8.8%, 0.7%−12.6%, and 2.9%−17.8%, respectively. Therefore, there is an increasing need to gauge the effect of climate change on future agricultural production systems to take necessary adaptation measures. Reducing the yield gap might be an option to address the issue of productivity improvement under changing climatic scenarios[13]. Although, scientists around the world have become successful in assessing the impact of changing weather parameters such as temperature and levels of CO2 on crop growth and development under a controlled environment[14], but the expensive setup and procedures prevent its adoption in developing countries. Projected climatic data coupled with crop simulation models are nowadays widely advocated for studying the impacts of climate change on crop productivity and for crop-level adaptations. They facilitate decision-making by quantifying and analyzing production risk using historical series of climate data and soil properties[15]. There are several Decision Support Systems (DSSs) in the form of computer software programs that make use of models and other information to make site-specific recommendations for betterment in agriculture production[16]. The DSSAT (Decision Support System for Agro Technology Transfer) is one such DSS which consists of widely used models that have been used in ~100 countries for more than 20 years[17]. In the DSSAT package, the Cropping System Model named the Crop Environment Resource Synthesis-Rice (CSM-CERES-Rice), is a decision-supporting tool that helps to understand and foresee the effect of discrete factors and complex interactions that have a major influence upon the growth and development of rice[18].

      The truthfulness of a model and its simulation result depends upon how precisely calibration and validation are carried out. The calibration of a model is an important step wherein the model parameters are adjusted to bring closeness between model output and real-world observations[19]. Daggupati et al.[20] also highlighted the importance of model calibration to increase model accuracy to decrease the uncertainty in the output of the model. The validation of a model is another important step to assess the performance of the model and it involves a comparison between observed and simulated data i.e. output generated by the model[21].

      In India the CERES-Rice model has been widely calibrated and validated to be used as a a research and agronomic tool[22]. Vijaylaxmi et al.[23] used the CERES-Rice model with an accuracy for NRMSE of 3% for heading and physiological maturity; 14% for biomass yield and 12% for grain yield for use in diverse agro-environments in Telangana state, India. The model was further used to evaluate various agronomic management practices for transplanted rice. Similarly, Chandravanshi et al.[24] reported good agreement between simulated and observed grain yield, anthesis, maturity and LAI of rice cultivar (Khadagiri) with RMSE value of 0.35 kg·ha−1, 0.96, 0.65, and 0.38, respectively in Madhya Pradesh state of India. Rajwade et al.[25] used the CERES-Rice model to determine the effects of methods of irrigation on the adaptation capacity of rice to climate change in the West Bengal state of India. They reported a good agreement between the predicted and observed data on the above-ground biomass with the d-index and NRMSE values of 0.99 and 0.13, respectively during the calibration of the model and 0.96 and 0.24, respectively during the validation of the model. As per Debnath et al.[13] the model showed good accuracy when calibrated and validated using the field experimental data for IR36 and Shankar cultivars in West Bengal, India. The NRMSE, R2, and D-index values of model performance were found to be 17.9%, 0.87%, and 0.97%, respectively, for the IR36, whereas it was 14.3%, 0.90%, and 0.98%, respectively, for the Shankar cultivar. These results revealed that the model could be further used for different purposes ranging from climate change impact assessment studies to the evaluation of agronomic management strategies.

      The present study was conducted with two main objectives. The first was to determine the genetic coefficients of commonly cultivated cultivars PR 126 and PR 127 of rice in Punjab state. The second objective was to use the validated model for optimizing the transplanting window of these commonly cultivated cultivars in Indian Punjab so that these windows could be used as an adaptive tool for rice cultivation under the ensuing climate change prediction scenarios.

    Materials and methods

    • The study was conducted at Punjab Agricultural University (PAU), Ludhiana, Punjab for two commonly sown cultivars of rice i.e., PR 126 (short duration) and PR 127 (long duration). Ludhiana is located at latitude and longitude of 30°54' N and 75°48' E, respectively, with an altitude of 247 m above mean sea level, it is located in the central plain region of Indian Punjab under the Trans-Gangetic agroclimatic zone of India. Rice seedlings of both cultivars were transplanted after 30 d of nursery planting in the main field on four different dates (17th June, 24th June, 1st July, and 8th July) in 2020 based on the recommended package of practices of Punjab Agricultural University (PAU) Ludhiana. The actual data needed for creating different files in DSSAT v4.7.5 viz.: crop management file, weather file, experimental data file, and soil file was extracted according to the necessity of the model. The CERES-Rice model was used for simulation which uses 11 different cultivar-specific parameters (CSPs) to determine the growth and development of particular crop varieties (Table 1).

      Table 1.  Cultivar Specific Parameters (CSPs) for CERES-Rice model.

      Genetic coefficientsDefinitionRange
      P1Thermal time during basic vegetative phase of the plant (expressed as growing degree days [GDD] above a base temperature of 9 °C).150−800 °C -d
      P20Photoperiod (longest day length, hours) at which the rate of development is maximum. At higher values than P2O, the developmental rate is slowed.11−13 h
      P2RExtent of delay in panicle initiation for each hour increase in photoperiod above P2O.5−300 °C -d
      P5Thermal time (in GDD) with a base temperature of 9oC from beginning of grain filling to physiological maturity.150−850 °C -d
      G1Potential spikelet number coefficient at anthesis.50−75 #/g
      G2Single grain weight (g) under ideal growing conditions.0.015−0.030 g
      G3Tillering coefficient (scalar value) relative to IR64 cultivar.0.7−1.3
      PHINTPhyllochron Interval (°C -d), thermal tme interval (in GDD) between each leaf-tip appearance under no stress conditions.55−90 °C -d
      THOTTemperature (°C), at temperature higher than this the spikelet sterility is affected.25−34 °C
      TCLDPTemperature (°C), at temperature lower than this the panicle initiation is further delayed (other than P1, P2O and P2R).12−18 °C
      TCLDFTemperature (°C) at temperature lower than this the spikelet sterility is affected.10−20 °C

      Sensitizing the genetic coefficients ofthe model

    • Sensitivity analysis is a process that helps us to understand how much the output of a particular crop model is sensitive concerning the different parameters of the model which are subject to uncertainty[26]. It helps to identify parameters that have a greater effect on phenology and yield of crop variety. For this study, the sensitivity analysis was done by calculating the sensitivity index (Eqn 1) based on the equation given by Lamsal et al.[27]. So in the present study firstly the CERES-Rice model was sensitized for 11 genetic coefficients before calibrating and validating it.

      SI=((O2−O1)/Oavg)/((I2−I1)/Iavg) (1)

      Where I1, I2, and Iavg are the minimum, maximum, and average input values of Cultivar Specific Parameters (CSPs) while O2, O1, and Oavg are model simulated values of crop parameters under study. The sensitivity index (SI) is a scientific approach to determine the importance of a parameter impacting the model output (yield, growth, duration, etc.). The range considered for calculating the sensitivity index (SI) of cultivar-specific parameters for both rice cultivars was taken the same as those mentioned in the 'RICER047.CUL' file. The DSSAT sensitivity analysis version 4.7.5.0 was used to generate the output data on anthesis, maturity, and yield for each unit increase in the coefficient of respective CSPs. On the other hand, a graphical approach was also used for quick visual interpretation of the most sensitive parameters, based on linearity in the graph drawn between input data and their respective outputs.

      Calibration and validation of the model

    • The GENCALC software which is inbuilt in the DSSAT package was used to calibrate the model for both of the rice cultivars PR 126 and PR 127. The calibration was done using the 24th June transplantation for both cultivars. Further, the genetic coefficients were adjusted by repeated iteration for more precision that could give lower RMSE values indicating accurate simulation. Multiple iterations were carried out to generate genetic coefficients which provided a good match between simulated and observed results.

      The calibration process was followed by the validation to check the accuracy of model simulations. The observed data from the transplantings done on 17th June, 1st, and 8th July on anthesis, physiological maturity, grain yield, and leaf area index (LAI) were compared with simulated values. Different statistical indices were used to evaluate the performance of the model. The coefficient of determination, i.e. R2 (Eqn 2) represents a good fit if the value is near to 1. The Root Mean Square Error, i.e. RMSE (Eqn 3) depicts the spread of residuals and its lower value represents the accuracy of the model. The d-stat is an index of agreement (Eqn 5) that covers both the biasness and the variability in the model simultaneously and it has better 1:1 prediction than R2[28]. Hence, if its value is near to 1, then it is considered to be excellent. The Normalized Root Mean Square Error (NRMSE) (Eqn 4) is another important statistical measure and its values < 10%, 10%−20%, 20%−30%, and > 30% indicate excellent, good, fair and poor fit between observed and simulated data[29]. The Nash-Sutcliffe model efficiency (EF) represents model efficiency (Eqn 6) and if its value is nearer to 1, then it means that the model is efficient[30]. The following are the formulas of various indices used in the current study:

      R2=1−∑ni=1(mi−si)2∑ni=1(mi−¯m)2 (2)
      RMSE=√∑ni=1(mi−si)2n (3)
      NRMSE=RMSE×100¯m (4)
      d-stat=1−∑ni=1(mi−si)2∑ni=1(|si|+|mi|)2 (5)
      EF=∑ni=1(mi−¯m)2−∑ni=1(si−mi)2∑ni=1(mi−¯m)2 (6)
      Deviationinyield/HI=Simulatedyield/HI−Averageyield/HIAverageyidle/HI (7)

      Where, mi = measured value of the parameter; si = simulated value of the parameter; n = number of observations; ¯m = mean of the observed parameter; HI = Harvest Index.

      The EasyGrapher v4.7.5 software was used for representing evaluation results through 1:1-line graphs.

      Optimizing the transplanting window for rice

    • The validated CERES-Rice model available in DSSAT v4.7.5 was used for simulating the transplanting window applicable for rice in Punjab i.e., 1st June to 20th July. The transplant age was kept as 30 days under the transplant tab in a crop management file, for simulating the yield of both the cultivars in all the transplanting dates assumed in the simulation. The temperature at the time of transplantation was changed for each date of planting according to the prevalent weather during the year 2020. The seven-day moving average was worked out to determine the best period of 7 days for transplanting these cultivars. The highest value of the grain yield in the seven days moving average was considered as the best time for transplanting.

    Results

      Sensitivity analysis of CERES-Rice model

    • The scientific approach was used to determine the sensitivity of days taken for anthesis and maturity as well as grain yield to the genetic coefficients (CSPs) of both the rice cultivars namely, PR 126 and PR 127 (Table 2). In the case of days taken for anthesis, P20 followed by P1, P2R, and PHINT were more sensitive for both the cultivars while P5, G1, G2, G3, THOT, TCLDP, and TCLDF were found insensitive. Similarly, for the days taken for physiological maturity, P20 followed by P1, P2R, P5, PHINT, and G3 were sensitive for both varieties of rice while other parameters were found insensitive for the same. Conversely, THOT was found to be highly sensitive for grain yield of both cultivars followed by P1, G2, P20, and G1 PHINT, while P2R, G3, and P5 remained less sensitive and TCLDP and TCLDF were almost insensitive. The genetic coefficients differ due to the genetic makeup of the variety and the location of the crop grown. Overall, in this study, yield was sensitized by THOT, P1, G2, P20, and G1 for both PR 126 and PR 127 while G1 and G2 were insensitive to anthesis and maturity. The sensitivity results for PR 126 and PR 127 are presented in Figs 1 & 2, respectively. It was found that there existed a linear relationship of days taken for anthesis and maturity with P20 and P1, respectively, while grain yield was found to be linearly related to THOT, P1, P20, and G2 for both PR 126 and PR 127 cultivars. This sensitization study of the model to CSPs (genetic coefficients) helped in the calibration and further validation of the model.

      Table 2.  Range and sensitivity index (SI) for phenology and yield and the range considered for the cultivar specific parameters (CSPs) for rice cultivars (PR 126 and PR 127).

      CSPsPR 126PR 127Range
      AnthesisMaturityGrain yieldAnthesisMaturityGrain yield
      P10.610.4310.60.420.95150−800
      P2R0.330.280.180.320.310.155−300
      P200.710.50.580.690.610.6611−13
      P500.250.1200.260.036150−850
      G1000.56000.5550−75
      G2000.68000.730.015−0.030
      G300.0150.1400.030.180.7−1.3
      PHINT0.280.170.430.250.220.3350−90
      THOT003.4003.328−34
      TCLDP000.025000.02412−18
      TCLDF000.016000.02810−20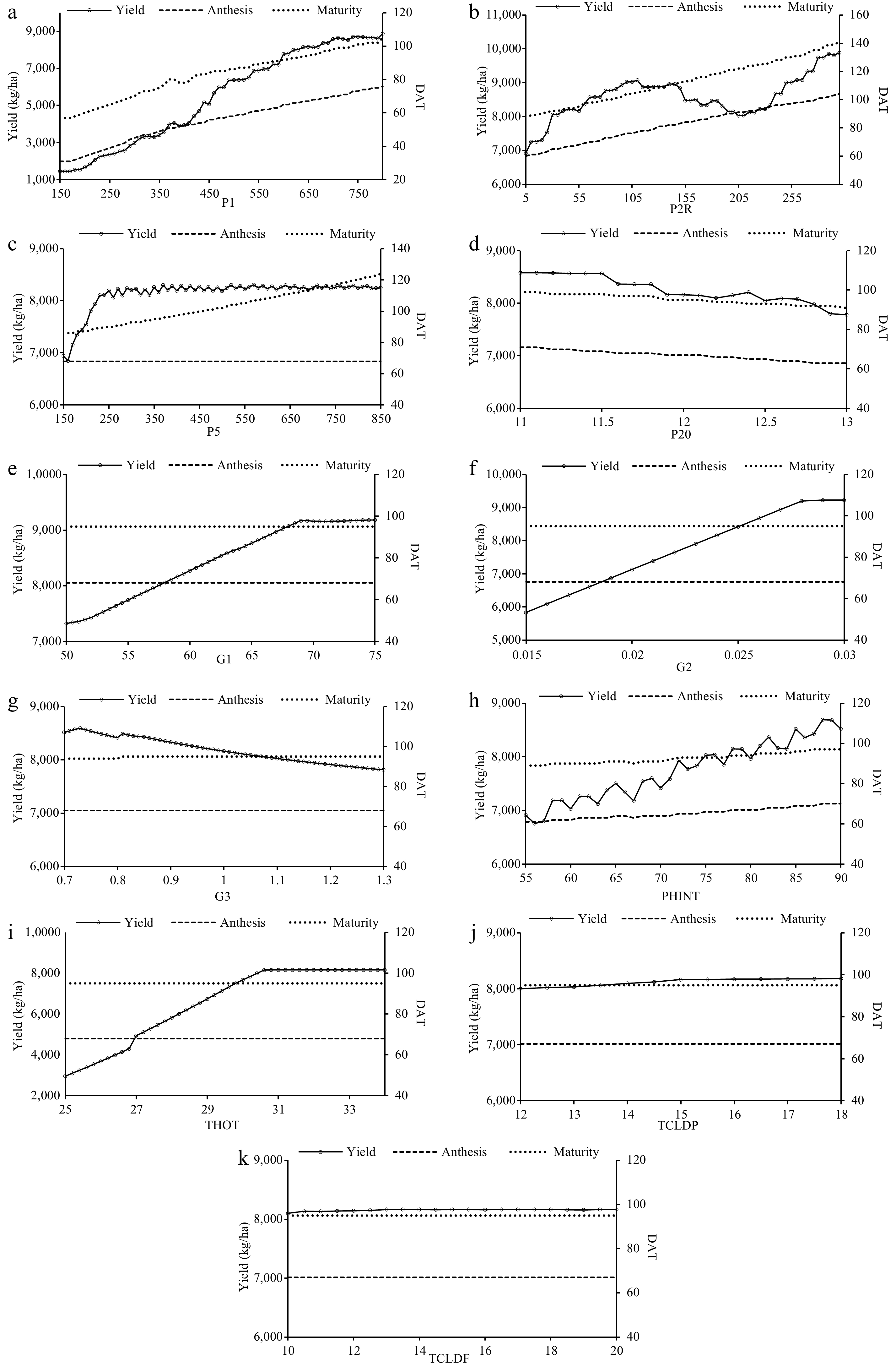

      Figure 1. 

      Variations in grain yield (kg·ha−1), anthesis and maturity (DAT) of PR 126 to changes in cultivar specific parameters. (a) P1, (b) P2R, (c) P5, (d) P20, (e) G1, (f) G2, (g) G3, (h) PHINT, (i) THOT, (j) TCLDP, and (k) TCLDF.

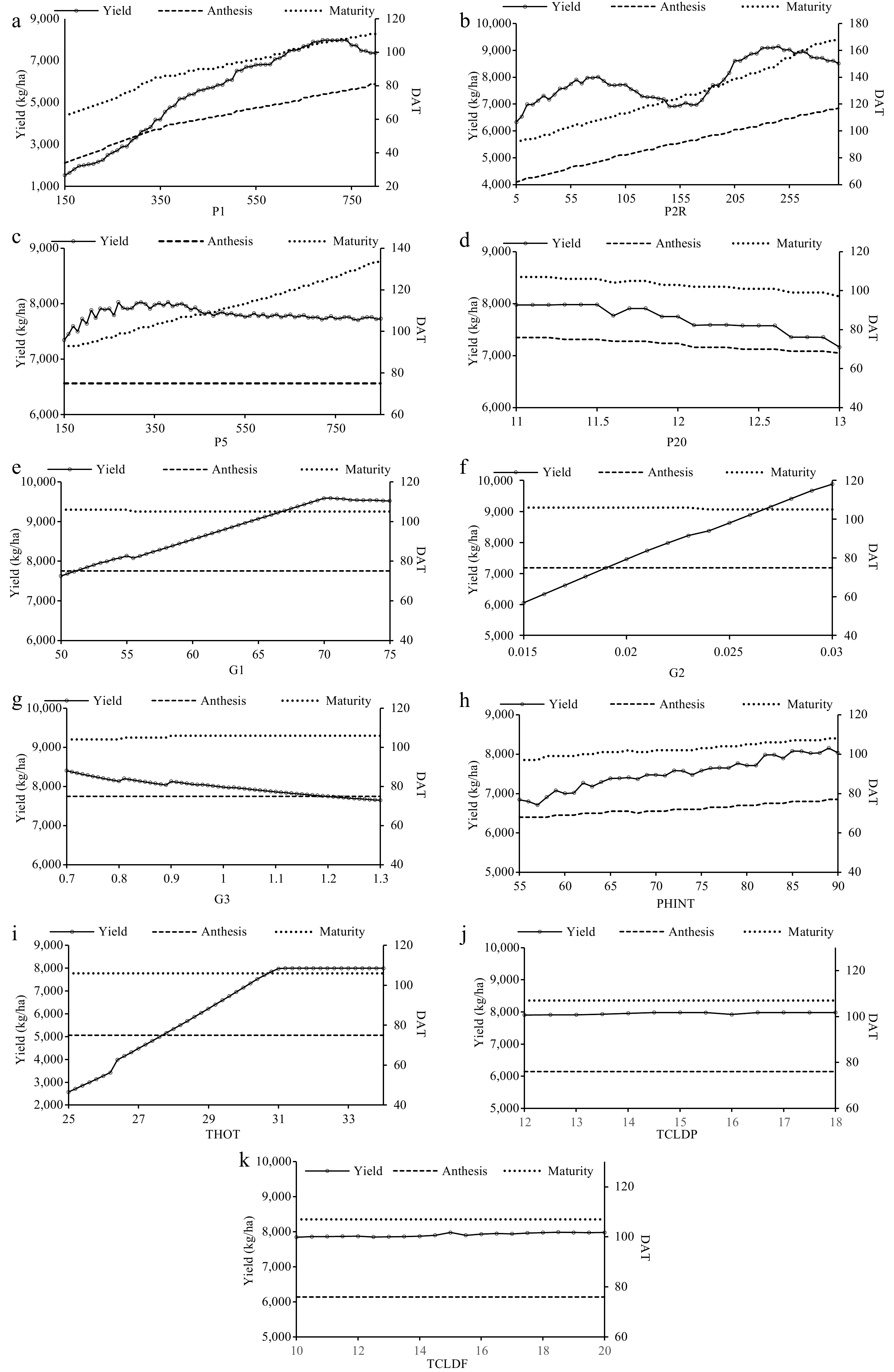
      Figure 2. 

      Variations in grain yield (kg·ha−1), anthesis and maturity (DAT) of PR 127 to changes in cultivar specific parameters. (a) P1, (b) P2R, (c) P5, (d) P20, (e) G1, (f) G2, (g) G3, (h) PHINT, (i) THOT, (j) TCLDP, and (k) TCLDF.

      Calibration of the model

    • After the sensitization of the CERES-Rice model to all the 11 CSPs, the calibration of the model was attempted for 24th June as the date of transplantation to determine the cultivar-specific parameters until there was close agreement between simulated and observed crop growth parameters. The genetic coefficients finalized after the iterations are given in Table 3. The values for CSPs namely P1, P2R, and P5 were found to be comparatively more for PR 127 than for PR 126. This represents the requirement of PR 127 for the longer period for its basic vegetative phase, more time required for panicle initiation and a longer time duration between grain filling to physiological maturity respectively. Conversely, coefficients defining critical photoperiod (P20), potential spikelet number (G1), and single grain weight (G2) were higher in the case of PR 126. Further evaluation of the performance of the model was done by using the above-stated statistical parameters for days taken for anthesis and maturity (DAT), LAI, and grain yield (kg·ha−1) of both the rice cultivars.

      Table 3.  Cultivar specific parameters used in calibration for rice cultivars.

      CultivarsCultivar specific coefficients
      P1P2RP5P20G1G2G3PHINTTHOTTCLDPTCLDF
      PR 126670.055.0360.012.059.00.0241.0083.031.015.015.0
      PR 127700.070.0400.011.353.40.0221.0083.031.015.015.0

      Validation of the model

    • After the calibration of the CERES-Rice model, it was further validated for the other three dates of transplanting using the statistical indices described in the previous sections. The observed and model-simulated averages for both rice cultivars (PR 126 and PR 127) were found to be close to each other for days taken for anthesis and maturity, LAI, and grain yield with their ratio near 1 (Table 4 and Fig. 3). The model satisfactorily simulated the days taken for anthesis and had an excellent value of R2 (0.94) for both cultivars of rice. Similarly, the model output for days taken to maturity was also in close agreement having R2 values of 0.89 and 0.96 for PR 126 and PR 127, respectively. The model satisfactorily simulated the days taken for the anthesis and maturity stages and the RMSE value was as low as 0.58 and 0.82 for PR 126, respectively, while it was 0.58 for both stages of PR 127. The validation results further depicted the calibration of the model with a high degree of certainity due to its high d-stat value for days taken anthesis and maturity for PR 126 to be 0.97 and 0.87, respectively, and for PR 127 to be 0.97 and 0.92, respectively. The value of NRMSE for days taken to reach the anthesis stage was found to be excellent for PR 126 (0.89%) and PR 127 (0.77%) cultivars. Similarly, for days taken to reach maturity, the NRMSE was found to be excellent for PR 126 (0.86%) and PR 127 (0.54%). The modeling efficiency (ME) was excellent for days taken to anthesis i.e., 0.88 (PR126) and 0.91(PR127) whereas it was good for days taken to maturity i.e., 0.57 (PR126) and 0.79 (PR 127).

      Table 4.  Statistical measures for evaluation of CERES-Rice v4.7.5 simulation performance

      ParametersPR 126PR 127
      ObservedSimulatedObservedSimulated
      Days taken for anthesis
      Mean days after transplanting (DAT)65657576
      Ratio1.011.00
      SD1.701.411.91.7
      R20.940.94
      RMSE0.580.58
      d-stat0.970.97
      NRMSE (%)0.890.77
      Model efficiency0.880.91
      Days taken for maturity
      Mean days after transplanting (DAT)9595107107
      Ratio0.991.00
      SD1.250.941.2470.816
      R20.890.96
      RMSE0.820.58
      d-stat0.870.92
      NRMSE (%)0.860.54
      Model efficiency0.570.79
      Grain yield
      Mean yield (kg·ha−1)8,2238,1817,8347,707
      Ratio1.00.98
      SD89.9158.9255.57339.22
      R20.890.98
      RMSE89.5155.5
      d-stat0.870.93
      NRMSE (%)1.091.98
      Model efficiency0.610.63
      Leaf area index (LAI)
      Mean LAI4.133.983.873.94
      Ratio0.961.02
      SD0.250.240.240.20
      R20.870.89
      RMSE0.180.12
      d-stat0.880.93
      NRMSE (%)4.333.00
      Model efficiency0.480.76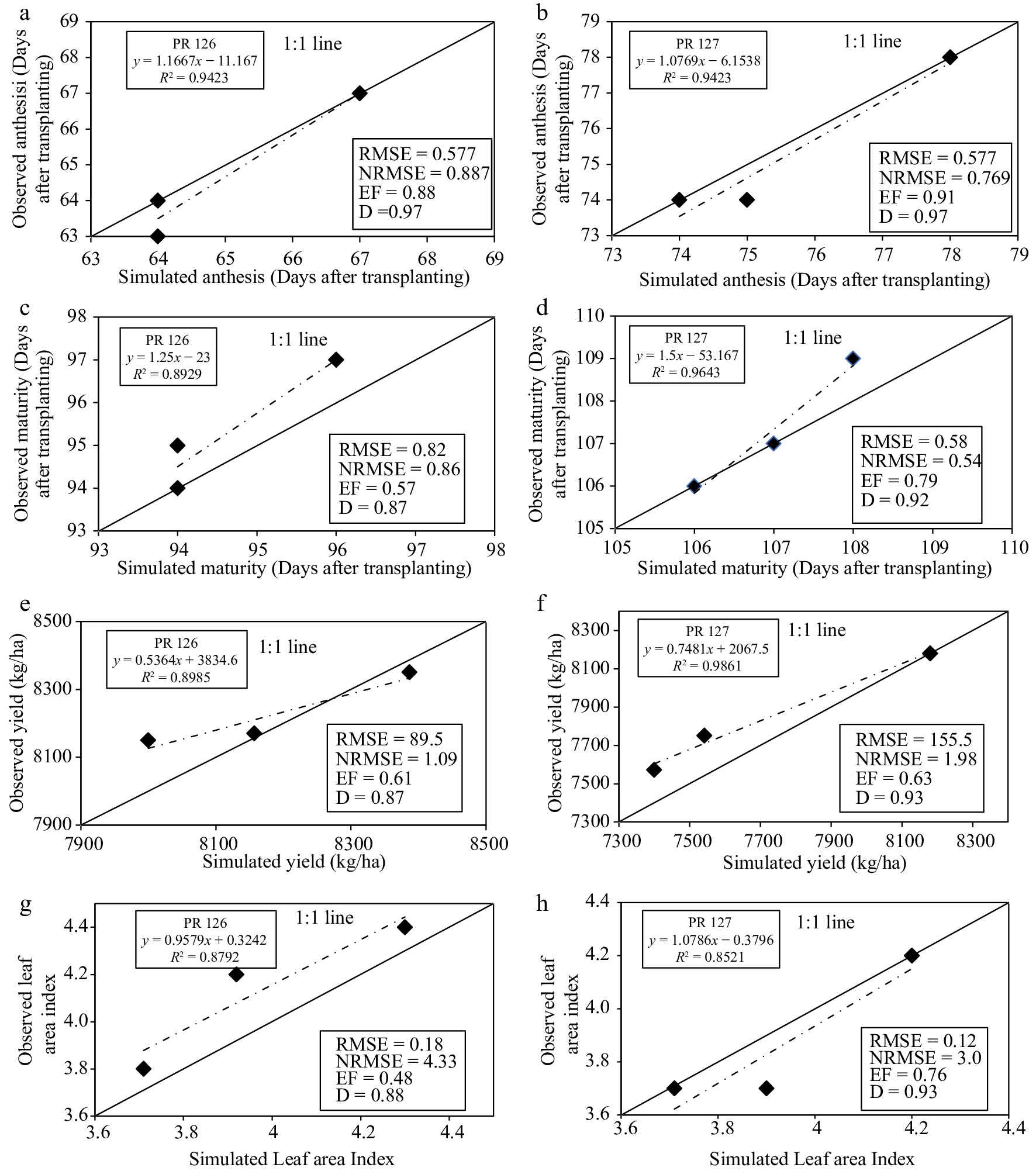

      Figure 3. 

      Evaluation results for (a), (b) anthesis, (c), (d) maturity, (e), (f) grain yield and (g), (h) LAI of rice cultivars

      The simulated average grain yield of the rice cultivars was closely related to observed values giving the mean ratio 1 and high R2 value of 0.89 for PR 126 and 0.98 for PR127. The RMSE was low with a value of 89.5 kg·ha−1 for PR 126 and 155.5 kg·ha−1 for PR 127 but the d-stat values were high for PR 126 (0.87) and PR 127 (0.93). The < 10% value of NRMSE, i.e., 1.09 and 1.98% for PR 126 and PR 127, respectively proved that the model gave an excellent fit with the selected values of CSPs. The values of modelling efficiency were in good range for both the rice cultivars i.e., 0.61 for PR 126 and 0.63 for PR 127.

      In the case of Leaf Area Index (LAI), the R2 value was excellent for PR 126 (0.87) and PR 127(0.89). The RMSE values were low and the d-stat values were high for PR 126, i.e. 0.18 and 0.88, respectively, and for PR 127, i.e. 0.12 and 0.93, respectively. The NRMSE was in a good range, i.e. 4.33% for PR 126 and 3.00% for PR 127. The modeling efficiency was also found to be fair for PR 126 (0.48) and good for PR 127 (0.76).

      Optimization of the transplanting window for rice

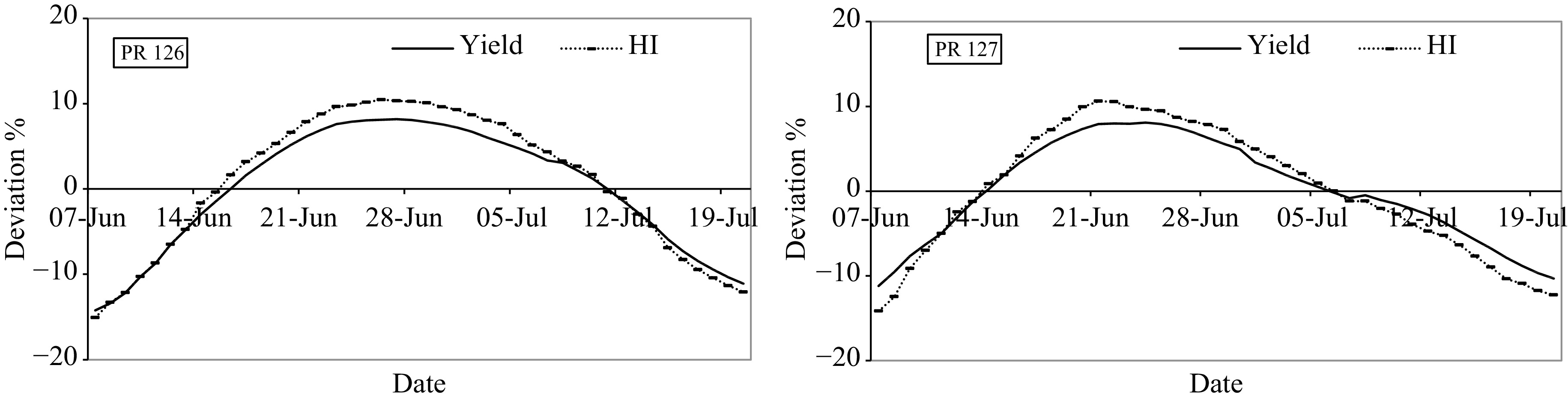
    • The sensitivity analysis, calibration, and finally validation of the CERES-rice model confirmed a good agreement between observed and simulated values of days taken for anthesis and maturity, LAI, and grain yield of both the rice cultivars. The calibrated and validated model was used to optimize the date of transplanting window for the rice cultivars. Generally, farmers of the Punjab region transplant 30−35 d seedlings of Parmal varieties in between mid-June to mid-July. So, the transplanting window was considered from 1st June up to 20th July for evaluation by taking the weekly average. The variability in grain yield and LAI for PR 126 and PR 127 within the transplanting window are presented in Fig. 4.

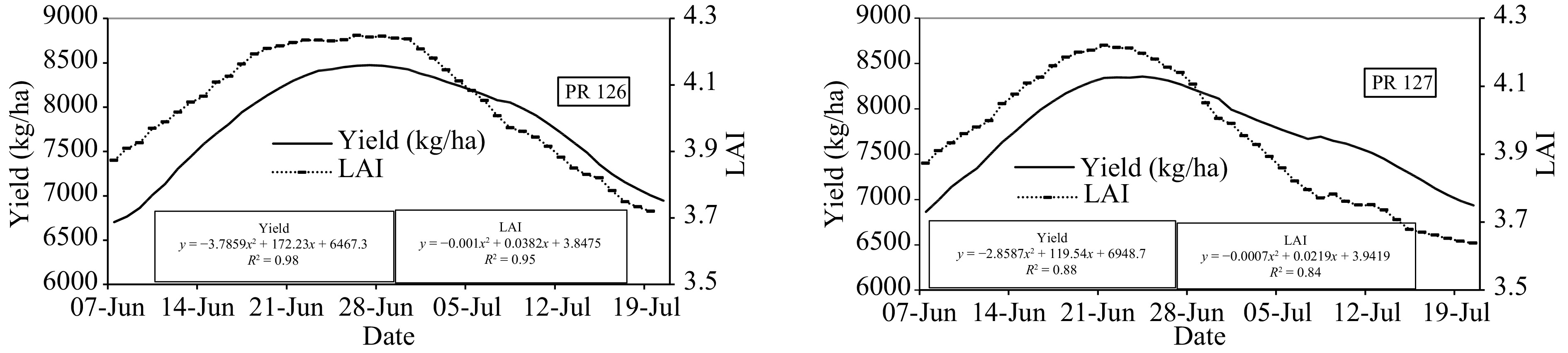
      Figure 4. 

      Grain yield and Leaf Area Index (LAI) (7-d moving average) relation with the transplanting window for rice cultivars PR 126 and PR 127.

      The results of the present study showed that the grain yield and LAI had a polynomial relationship with the transplantation date. The simulation results on a weekly average basis indicated 24th to 30th June for PR 126 and 20th to 26th June for PR 127 as the optimum transplanting window with grain yield and LAI for PR 126 ranging between 8,425−8,473 kg·ha−1 and 4.23−4.24, respectively and for PR 127 between 8,298−8,356 kg·ha−1 and 4.20−4.21, respectively. The minimum yield of both cultivars was observed on 7th June i.e. early transplanted rice with grain yield and LAI being 6,703 kg·ha−1 and 3.8, respectively for PR 126 and 6,865 kg·ha−1 and 3.9, respectively for PR 127. The coefficient of determination (R2) of grain yield and LAI was 0.98 and 0.94, respectively for PR 126 and 0.89 and 0.84, respectively for PR 127, thereby indicating a very good agreement between observed and simulated values. The polynomial regression model was able to explain more than 80% variation in grain yield and LAI with the date of transplantation for both cultivars.

      The deviation of grain yield and HI (Harvest index) from the mean, clearly depicted the reduction in HI as a result of a reduction in the grain yield of rice (Fig. 5). The deviation of the grain yield and HI of PR 126 varied between −14.2 to +8.2% and −15.1 to +10.5% respectively, while for PR 127 deviations varied between −11.2 to +8.1% and −14.2 to +10.6%, respectively. The negative deviation in the yield/ HI from the average in the case of late transplantation for PR 126 and PR 127 was observed after 11th July and 6th July, respectively. On the other hand, in the case of earlier transplantation, the model showed depreciation in yield and HI when transplanted before the 15th of June for PR 126 and the 13th of June for PR 127. The negative effect on yield and HI of both the cultivars which occurred in case of early and late transplantation could be due to unfavourable climatic conditions during the critical phenological stages of rice.

      Figure 5. 

      Grain yield and harvest index (HI) relation with the sowing window for PR 126 and PR 127.

    Discussion

      Sensitivity analysis and calibration of CERES-Rice model

    • In a dynamic crop simulation model the genetic coefficients determine the growth and development characteristics of different cultivars of the crop. In the CERES-Rice model available in DSSAT V4.7.5 there are 11 genetic coefficients (CSPs) for rice cultivars. In the present study sensitivity analysis for 11 CSPs for rice cultivars namely PR 126 and PR 127 was done to determine their sensitivity index and performance of the crop. Amongst the two phenological stages, i.e. the days taken to anthesis of rice cultivars were observed to be sensitive to mainly four CSPs (P20, P1, P2R, and PHINT) and physiological maturity to 6 CSPs (P20, P1, P2R, P5, PHINT, and G3). The grain yield of rice cultivars was highly sensitive to THOT followed by P1, G2, P20, and G1 PHINT while it was less sensitive to P2R, G3, and P5. Ge et al.[31] have reported that genetic coefficients determine the simulation of the growth behavior of crops. They observed that the P20 coefficient influences all the outputs of the CERES-Rice model and so affects the growth and phenology of rice cultivars. The calibration of a model is done to determine the optimum values of its CSPs[22]. Calibration of the CERES-Rice model revealed that the values for coefficients P1, P2R, and P5 were found to be comparatively more for cv PR 127 than cv PR 126 since its growth duration is more by nearly 10 d. So it takes a longer time to complete its vegetative growth and initiate the panicle development. The values of the yield governing coefficients, i.e. P20, G1, and G2 for cv PR 126 were more thereby representing its higher yield potential. Similar results have been reported by Goswami & Dutta[32] for CERES-Rice model cultivar specific coefficients. They have discussed a variation in CSPs used by different workers in their studies at a global level.

      Validation of the CERES-Rice model

    • The CERES-Rice model was validated for three dates of transplanting for two cultivars (PR 126 and PR 127) and the statistical indices, i.e. R2, Mean ratio, RMSE, ME, d-Stat and NRMSE indicated a good performance of the model. Similarly, Mote & Kumar[33] calibrated three rice cultivars using the CERES-Rice model under three sowing dates and N levels and they further validated it for biomass and grain yield of rice. The validation results showed RMSE, MBE, and PE for grain yield to be 5.3, −4.1, and PE, respectively while for biomass yield to be 7.4, −5.9, and 9.8, respectively. The model was further used to simulate the growth and development of rice as affected by varying levels of nitrogen in Navsari, Gujrat (India). Ray et al.[34] observed a good agreement between simulated and observed grain yield of Swarna variety of rice with a RMSE value of 0.82 t·ha−1 and a NRMSE value of 14.9%. The index of agreement (0.869) for grain yield also revealed that the model satisfactorily predicted the grain yield of rice. Jha et al.[35]evaluated the model for its application in Bihar, India. The values for statistical measures as obtained for yield, panicle initiation, anthesis, and maturity were 4.04%, 2.14%, 1.04%, and 1.00%, respectively for NRMSE; 0.87, 0.92, 0.91, and 0.81, respectively for d-index; and 0.75, 0.66, 0.81, and 0.58, respectively for ME. Goswami & Dutta[32] compiled evaluation results of the CERES-Rice model on crop phenology and grain yield and found that NRMSE values varied from 1%−5%, 1%−4%, and 0.05%−5% for anthesis, physiological maturity, and grain yield, respectively. In the present study the observed and simulated days taken for phenological stages, i.e. anthesis and physiological maturity, growth attribute (LAI), and grain yield for the rice cultivars were also compared using the 1:1-line graph. These line graphs prepared in Easy-Grapher[36] which is an in-built program of DSSAT depicted a good fit between the observed and simulated values. These graphs help in the quick visual interpretation of validation results and this graphical display is designed to expedite statistical validation which would otherwise take significant time and effort.

      Optimization of transplanting window for rice

    • Dynamic simulation models have been widely used to determine the optimum sowing period for crops[37, 35, 38]. In Punjab state generally, 30−35 d old seedlings of Parmal varieties are transplanted between mid-June to mid-July. So the calibrated and validated CERES-Rice model was used to fine-tune the transplanting window for the two rice cultivars (PR 126 and PR 127). The study highlighted a polynomial relationship of transplantation date with the LAI and grain yield. So the simulation on a weekly average basis showed that the 24th to the 30th June for cv PR 126 and the 20th to the 26th June for PR 127 would be the optimum transplanting period. There could be various reasons for the highest yield simulated by the model for rice transplanted between the 20th to the 30th June. Firstly, in Punjab, transplanting of rice near the 25th June helps in aligning the growth and development of rice with the monsoon rainfall that hits Punjab from the 1st week of July[3]. Secondly, optimum climatic requirements for important stages viz.: flowering and tillering of crops might have been fulfilled when transplanted during this period. A study conducted by Brar et al.[39] in North-west India revealed that rice crops transplanted during the last week of June encountered more favorable weather (particularly temperature and sunshine) during the tillering stage as compared to early and late transplanted crops, thus, leading to a higher number of panicles/m2 and test weight. It also reduced the spikelet sterility in rice which ultimately resulted in higher grain yield. Contrarily, later transplantation showed declination in the yield and the reasons could be a reduction in panicle length, a decrease in number of kernels per panicle, and spikelet sterility. Kushuwaha[40] found that delayed transplantation of different genotypes of rice in Nepal decreased plant height, panicle length and number of kernels per panicle. Singh et al.[41] used the CERES-Rice model to determine the optimum dates of planting of different rice varieties in different locations of India, i.e. PR 118 (Ludhiana and Amritsar), HKR6 (Hisar and Ambala), Pant-4 (Kanpur) and Sugandha 1126 (Modipuram). The simulation results showed that the yield was maximum in case of Ludhiana/Amritsar when June 24 was considered as the transplanting date whereas 15th July was found to be the best transplanting date of rice in Hisar, Ambala, Kanpur, and Modipuram. Vishwakarma et al.[42] observed 27th June to be an appropriate time for transplanting of rice hybrids in Uttar Pradesh. Similarly, Deka et al.[43] conducted research at Assam, India during 2014−2015 and 2015−2016 in which they observed that rice transplanted on 20th June gave the highest yield than those transplanted during later dates.

    Conclusions

    • Rice is the only crop to survive waterlogged anaerobic conditions and one of the major cereal crops of the entire world. The demand of rice may never decrease, however, its supply can definitely decline. For the unprecedented climate variability and unforeseen future climate changes, it is not an easy task to predict the yield of rice within a short time for present and future climatic scenarios under field conditions. The DSSAT suite of simulation models is one of those decision-making tools that not only predicts yield within a short period but also helps in optimizing management practices that include transplanting date, fertilizer and irrigation application, seedlings per hill, and so on.

      The results of the DSSAT package highly depends upon the accuracy of sensitivity analysis followed by proper calibration and validation. Thus the identification of the most sensitive crop-specific parameters helps in accurate calibration of the model. In the above study, a precisely calibrated CERES-Rice model available in DSSAT version 4.7.5 was used and it was further checked by validating it for its reliability with various statistical measures (R2, d-stat, RMSE, NRMSE, SD, and EF). All the statistical measures showed close agreement between values of simulated and observed parameters.

      The calibrated CERES-Rice model was then used to optimize the transplanting window for rice. Overall, it simulated the 24th to the 30th of June for PR 126 and 20th to the 26th of June for PR 127 as the optimum transplanting window in Punjab. Both early and later transplantations showed a reduction in yield from the optimized transplanting window yield. Punjab has always been distinguished for its contribution in the 'Green revolution' but with an increasing variability in driving elements of climate change, farmers have been facing challenges in gaining the same amount of rice yield as in prior climatic conditions. Depletion in yield can be caused by improper management practices involved and it is always needed to evaluate and re-evaluate management practices that contribute towards the grain yield of the crop. Thus the CERES-Rice model available in the DSSAT package is a powerful tool that helps in determining optimum management practices without the involvement of tedious field experiments.

    Author contributions

    • The authors confirm contribution to the paper as follows: experimental operation, data analysis and draft manuscript preparation: Aryal A; study conception and design, study supervision, manuscript revision/finalization: Kaur P; field experiments conduction: Sandhu SS; draft manuscript preparation: Kothiyal S. All authors reviewed the results and approved the final version of the manuscript.

    Data availability

    • The datasets generated or analyzed during this study are included in the manuscript.

      Acknowledgments

      • The funding for the research was received from the Science and Engineering Research Board, New Delhi through Core Grant project funding No. CRG/2019/002856 : 'Optimizing cereal productivity under RCP projected climatic scenarios by mid and end of 21st century in Punjab' is duly acknowledged. The actual field datasets used for calibration and validation of CERES-Rice model collected under the Indian Council of Agricultural Research (ICAR)-Central Research Institute for Dryland Agriculture (CRIDA) research scheme 'All India Coordinated Research Project on Agrometeorology' is duly acknowledged.

      Conflict of interest

      • The authors declare that they have no conflict of interest.

      Rights and permissions
      • Copyright: © 2024 by the author(s). Published by Maximum Academic Press, Fayetteville, GA. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
    Figure (5)  Table (4) References (43)
  • About this article
    Cite this article
    Aryal A, Prabhjyot-Kaur, Sandhu SS, Kothiyal S. 2024. Optimizing the transplanting window for higher productivity of short and medium duration rice cultivars in Punjab, India using CERES-Rice model. Circular Agricultural Systems 4: e011 doi: 10.48130/cas-0024-0010
    Aryal A, Prabhjyot-Kaur, Sandhu SS, Kothiyal S. 2024. Optimizing the transplanting window for higher productivity of short and medium duration rice cultivars in Punjab, India using CERES-Rice model. Circular Agricultural Systems 4: e011 doi: 10.48130/cas-0024-0010
    shu

Catalog

  • HTML

  • Introduction
  • Materials and methods

  • Sensitizing the genetic coefficients ofthe model

  • Calibration and validation of the model

  • Optimizing the transplanting window for rice

  • Results

  • Sensitivity analysis of CERES-Rice model

  • Calibration of the model

  • Validation of the model

  • Optimization of the transplanting window for rice

  • Discussion

  • Sensitivity analysis and calibration of CERES-Rice model

  • Validation of the CERES-Rice model

  • Optimization of transplanting window for rice

  • Conclusions
  • Author contributions
  • Data availability
  • Acknowledgments
  • Conflict of interest
  • Rights and permissions
  • About this article
logo

Contents

Policies

Services

Partnerships

© 2025 Maximum Academic Press, except Open Access articles. MAP is a member of ALPSP, COPE, CrossRef, cOAlition S, OASPA and STM.

Privacy Policy  |  Site Map  |  Terms and Conditions

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return