-
The global energy landscape is rapidly evolving[1−3], with a growing emphasis on sustainable and resilient electricity supply systems[4−6]. Microgrids, as localized and self-contained energy networks, have emerged as a promising solution to enhance the resilience and reliability of power supply, particularly in the face of increasing natural hazards such as hurricanes, wildfires[7, 8], earthquakes, and extreme weather events[9, 10]. As these hazards become more frequent and severe due to climate change[11−13], it is imperative to develop effective strategies that mitigate their impact on microgrids and bolster their ability to adapt to changing conditions.
This research aims to address the critical need for comprehensive evaluations of mitigation and adaptation strategies within the context of microgrids exposed to natural hazards.
Existing research
-
The field of electricity grid landscapes and their vulnerabilities to natural hazards has garnered significant attention from researchers and practitioners alike.
Existing research has recognized the potential of microgrids in enhancing the resilience of electricity supply systems against a range of natural hazards[14, 15]. Studies such as that by Eskandapour et al.[16] have examined the ability of microgrids to maintain power supply during extreme weather events, including hurricanes[17] and wildfires[18]. Other research, such as that of Shojaeiyan et al.[15], has explored the role of microgrids in providing reliable energy access in earthquake-prone regions.
Previous investigations, such as that of the Global Facility for Disaster Reduction and Recovery[19], have explored various strategies to mitigate the impact of natural hazards on microgrids. Additionally, other research efforts[20, 21] have emphasized the importance of community engagement and stakeholder acceptance in designing effective microgrid resilience strategies.
Knowledge gaps and originality of this study
-
While significant progress has been made in understanding microgrid resilience and evaluating mitigation and adaptation strategies, several knowledge gaps remain that warrant further investigation. Addressing these gaps will contribute to a more comprehensive and nuanced understanding of microgrid resilience in the face of natural hazards.
While previous studies have assessed individual microgrid strategies for resilience enhancement, there is a lack of comprehensive evaluation frameworks that consider a wide array of criteria simultaneously. The proposed article's incorporation of multiple criteria, including effectiveness, scalability, community engagement, and environmental impact, bridges this gap by providing a more holistic understanding of strategy effectiveness and trade-offs.
Existing research often focuses on specific natural hazards and their impacts on microgrids in isolation. This article's approach to comprehensively exploring various types of natural hazards, such as hurricanes, wildfires, and earthquakes, and their implications for different grid landscapes (centralized, micro, nano, and smart), contributes to a more robust understanding of the complex interactions between hazards and grid types.
While some studies touch upon the environmental implications of microgrid strategies, there is a dearth of quantitative assessments that systematically quantify the environmental trade-offs of various resilience measures. The inclusion of environmental impact as a criterion in the proposed evaluation framework addresses this gap, offering insights into the ecological implications of different strategies.
While the importance of stakeholder engagement is recognized, the article's focus on community engagement as a distinct criterion acknowledges the need for a deeper exploration of how local communities perceive and accept different resilience strategies. This approach highlights the critical role of community dynamics and perceptions in the success of microgrid initiatives.
While scalability and long-term sustainability are acknowledged as essential factors, few studies delve into the interaction between the maturity of technologies and their long-term sustainability. The incorporation of technological maturity as a criterion offers a fresh perspective on the practicality and longevity of different strategies.
The proposed consideration of education and training as a criterion recognizes a significant gap in the literature. Few studies explore the educational needs of stakeholders involved in microgrid operation and management, highlighting the originality of this article in addressing a critical aspect of strategy implementation.
Existing research often treats microgrid resilience strategies in isolation without exploring their potential synergies or conflicts when combined. The proposed article's focus on the integration of strategies and their compatibility with existing or planned measures contributes to a more nuanced understanding of strategy interplay.
While regulatory compliance is often mentioned, there is limited exploration of the alignment or misalignment of microgrid strategies with existing policies and regulations. The proposed article's inclusion of regulatory and policy compliance as a criterion provides insight into the institutional barriers and enablers of strategy implementation.
By addressing these knowledge gaps, the article offers a novel and comprehensive perspective on microgrid resilience in the face of natural hazards. It contributes to the advancement of microgrid planning and design by providing a multidimensional evaluation framework that considers diverse criteria, ultimately aiding decision-makers and practitioners in developing more effective and contextually relevant strategies.
Research questions
-
This article aims to provide a comprehensive analysis of microgrid resilience strategies in the context of natural hazards. Specifically, it seeks to answer the following research questions:
(1) How do different types of electricity grid landscapes (centralized grids, microgrids, nanogrids, and smart grids) respond to and interact with various types of natural hazards, such as hurricanes, wildfires, earthquakes, and extreme weather events, and what are the implications for their resilience and reliability?
(2) How can a Multi-Criteria Decision-Making approach, such as the Analytic Hierarchy Process (AHP), be employed to evaluate and prioritize various mitigation and adaptation strategies for microgrids facing natural hazards, considering multiple criteria?
Outline
-
Following the comprehensive introduction, covering our research motivation, existing studies, knowledge gaps, and research questions, our focus shifts. In the next section, we present the hierarchical framework for decision-making, elucidate interconnections among criteria, alternatives, and criteria–alternatives interactions, and detail the data collection and processing procedures. Additionally, we delve into the entropy within the Multi-Criteria Decision Making (MCDM) Universe, placing particular emphasis on MCDM types such as TOPSIS, ELECTRE, PROMETHEE, and AHP. We elaborate on the rationale behind choosing AHP over other alternatives, such as Fuzzy AHP or hybrid MCDM. Furthermore, we explore various applications and steps of the MCDM-AHP framework.
Moving forward, we share the outcomes of our study, providing insights into the responses of different electricity grid landscapes to natural hazards and the evaluation of mitigation and adaptation strategies using the MCDM-AHP framework.
Concluding our exploration, we meticulously dissect the strategies against specific criteria, extrapolate from the findings to offer practical insights tailored for policymakers, energy planners, and practitioners, compare the findings with existing studies, and candidly present the limitations of our study along with avenues for future research.
In the concluding section, we synthesize the key findings and contributions of our study, drawing from the comprehensive exploration undertaken in the preceding sections.
This structured approach aims to provide a clear and cohesive narrative of our research process and outcomes, with a particular emphasis on the entropy aspect within the MCDM framework.
-
Multi-Criteria Decision Making (MCDM) is a powerful analytical approach employed in various fields to facilitate decision-making processes involving multiple and often conflicting criteria. The MCDM universe encompasses a diverse array of methodologies, each designed to address different aspects of decision problems. These methodologies assist decision-makers in evaluating and ranking alternative solutions based on multiple criteria, considering the complexity and interdependence of the decision factors.
One of the widely adopted techniques within the MCDM framework is the Analytic Hierarchy Process (AHP). AHP provides a structured and systematic approach to decision-making by breaking down complex problems into a hierarchical structure of criteria and alternatives. It allows decision-makers to assign weights to criteria, compare alternatives pairwise, and derive overall rankings[22, 23].
Entropy, in the context of MCDM, refers to the measure of uncertainty or randomness in decision-making processes. Entropy can be utilized to quantify the degree of disorder or lack of information in the decision system. In the MCDM universe, incorporating entropy into decision models is essential for addressing uncertainties and enhancing the robustness of decision outcomes.
Entropy-based methods within MCDM aim to manage the information content and variability associated with decision criteria and alternatives. By considering entropy, decision-makers can gain insights into the diversity and complexity of the decision problem, enabling more informed and adaptive decision strategies.
MCDM encompasses diverse methodologies, including grey relational analysis (GRA), complex proportional assessment (COPRAS), and weighted aggregated sum product assessment (WASPAS)[24].
TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) is a widely used MCDM technique that evaluates alternatives based on their proximity to the ideal solution and furthest from the negative ideal solution. It considers both positive and negative aspects, making it suitable for real-world decision scenarios[25].
ELECTRE (Elimination and Choice Translating Reality) is another MCDM method that focuses on outranking alternatives rather than assigning precise numerical values. It considers partial preferences and allows for a more flexible representation of decision-maker preferences[25].
PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluations) is designed to handle decision problems with multiple conflicting criteria. It generates a preference ranking for alternatives by comparing them pairwise, considering criteria weights and decision-maker preferences[26].
AHP, a widely recognized MCDM technique, focuses on pairwise comparisons of criteria and alternatives to determine their relative importance[27, 28]. AHP is often integrated with other MCDM techniques to enhance its capabilities. For example, combining AHP with TOPSIS[29] allows for a comprehensive analysis that considers both subjective criteria weights (from AHP) and objective performance measures (from TOPSIS). AHP can also be integrated with ELECTRE[30] or PROMETHEE[31] to address the shortcomings of strict outranking methods by incorporating the cardinal information provided by AHP.
By exploring various MCDM techniques and their integration with AHP, decision-makers can tailor their approach to the specific nuances of the decision problem at hand, ensuring a more robust and comprehensive evaluation of strategies for mitigating and adapting to natural hazards in electricity grid landscapes.
MCDM techniques find application across various fields, such as engineering[32, 33], management[34, 35], environmental science[36, 37], and decision analysis, such as identifying suitable regions for photovoltaic and concentrated solar power projects[38, 39], onshore[40] and offshore wind energy feasibility[41], and offshore floating photovoltaic installations[42, 43]. MCDM-AHP has been extensively used for complex decision-making scenarios, including project selection[44, 45], resource allocation[46, 47], risk assessment[48, 29], and evaluation of strategies for resilience enhancement[49].
Furthermore, the specialized utilization of MCDM-AHP has expanded to the field of cybersecurity solutions within smart grid environments, highlighting its integration with artificial intelligence[50, 51], as evidenced in a recent study by Bouramdane[52]. Moreover, the same researcher has employed this approach to evaluate water management strategies in smart cities[53], encompassing water desalination applications[54].
In a recent investigation, Bouramdane[55] conducted a comprehensive evaluation of hydrogen production technologies in Morocco. Employing the MCDM-AHP methodology, their assessment considered factors such as technological feasibility, economic viability, environmental impact, and social acceptance. The study identified high-performing technologies, including Autothermal Reforming with Carbon Capture and Storage, as well-suited for hydrogen production in Morocco. Additionally, promising performance was observed in moderate-performing technologies like photovoltaic and concentrated solar power. However, low-performing technologies may face challenges in meeting specified criteria. The research underscores the importance of stakeholder perspectives, particularly in renewable penetration scenarios, influencing technology suitability. These insights play a crucial role in guiding decision-makers toward achieving energy independence and climate goals. For a more detailed understanding of hydrogen technologies, readers are encouraged to refer to the previous work of Bouramdane[56−60].
The selection of an appropriate decision-making methodology is paramount in ensuring the robustness and reliability of the assessment process. In our research endeavor focused on evaluating strategies for mitigating and adapting to natural hazards within electricity grids, we have deliberately opted for the exclusive use of the Analytic Hierarchy Process (AHP) as our preferred Multi-Criteria Decision-Making (MCDM) framework. Below, we elucidate the rationale behind our decision, examining why AHP was chosen over alternative methodologies such as Fuzzy AHP or hybrid MCDM methods.
● Precision in pairwise comparisons: AHP is renowned for its ability to handle complex decision problems by breaking them down into simpler, more manageable components. The methodology excels in eliciting and quantifying the preferences of decision-makers through pairwise comparisons. By allowing experts to systematically compare the relative importance of criteria and alternatives, AHP provides a structured approach to capture precise judgments. This precision is crucial in the context of our research, where the intricate nuances of each mitigation and adaptation strategy, as well as the diverse array of natural hazards, demand a granular understanding to derive meaningful conclusions.
● Transparency and ease of interpretation: AHP offers transparency in the decision-making process, making it an accessible and comprehensible method for both experts and stakeholders involved in the evaluation. The methodology provides a clear hierarchy of criteria and alternatives, allowing for straightforward interpretation of results. This transparency is essential for fostering a shared understanding among diverse stakeholders, including policymakers, industry professionals, and community members. In the context of our research, where community engagement and stakeholder acceptance (C5) are integral criteria, the simplicity and transparency afforded by AHP contribute significantly to the overall robustness of our decision-making framework.
● Consistency and sensitivity analysis: One of the distinct advantages of AHP is its built-in mechanism for assessing the consistency of expert judgments. The methodology employs a consistency ratio, enabling researchers to identify and rectify inconsistencies in pairwise comparisons. This feature enhances the reliability of the derived weights and ensures the stability of the decision model. Moreover, AHP facilitates sensitivity analysis, allowing us to gauge the impact of variations in expert judgments on the final outcomes. In a complex and dynamic field like natural hazard mitigation and adaptation in electricity grids, where uncertainties abound, the ability to assess and address the sensitivity of the results is invaluable.
● Specificity to pairwise comparison: While Fuzzy AHP and hybrid MCDM methods introduce additional layers of complexity and abstraction through fuzzy logic and integrative techniques, AHP's straightforward approach is advantageous in our context. The specificity of pairwise comparisons aligns seamlessly with our research objectives, allowing for a direct and unambiguous assessment of the strategies in relation to the identified criteria. This directness is particularly pertinent when dealing with a diverse range of natural hazards and multiple criteria, as it ensures a focused and contextually relevant evaluation.
● Scalability and adaptability: AHP's scalability and adaptability to a broad spectrum of decision problems make it a versatile choice for our research. The methodology accommodates a large number of criteria and alternatives without compromising the integrity of the decision model. This scalability is critical in our multi-dimensional evaluation of strategies for electricity grid resilience. AHP's adaptability also allows for the incorporation of evolving factors, such as emerging technologies and changing regulatory landscapes, enhancing the longevity and relevance of our findings.
In summary, the exclusive use of AHP in our research is grounded in its precision, transparency, consistency, specificity to pairwise comparisons, and scalability. These characteristics collectively contribute to the reliability and applicability of our MCDM framework in assessing strategies for mitigating and adapting to natural hazards within diverse electricity grid configurations. While acknowledging the merits of alternative methodologies, our deliberate selection of AHP is aligned with the intricacies and objectives of our research, ensuring a robust foundation for decision-making in the realm of resilience enhancement and risk reduction within electricity grids.
The AHP involves several key steps to systematically assess alternatives based on predefined criteria[61, 62]. These steps include:
(1) Problem definition and hierarchy construction: Clearly define the decision problem and organize it hierarchically, consisting of the main objective, criteria, sub-criteria, and alternatives.
(2) Pairwise comparisons: Assess the relative importance of criteria and alternatives by pairwise comparisons. The Saaty scale, ranging from 1 to 9, is often used to express the degree of preference. Let
$ n $ $ {\text{A}} = \begin{bmatrix} 1 & a_{12} & \cdots & a_{1n} \\ \dfrac{1}{a_{12}} & 1 & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \dfrac{1}{a_{1n}} & \dfrac{1}{a_{2n}} & \cdots & 1 \\ \end{bmatrix} $ Where
$ a_{ij} $ $ i $ $ j $ (3) Calculation of priority weights: Compute the priority weights for criteria and alternatives by analyzing the pairwise comparison matrix. The normalized eigenvalue method or eigenvector method is employed to derive these weights. The priority vector W is calculated by normalizing the principal eigenvector of A:
$ {\text{W}} = \dfrac{1}{\lambda} {\text{A}} {\text{W}} $ Where:
$ \begin{array}{l} {\text{W}} = \text{Priority vector of size } n \times 1 \\ \lambda = \text{Principal eigenvalue of matrix A } \end{array}$ (4) Consistency check: Evaluate the consistency of judgments using the consistency ratio (CR) to ensure the reliability of the pairwise comparisons:
$ CR = \dfrac{CI}{RI} $ Where:
$ CI = \dfrac{\lambda - n}{n - 1} $ RI = Random index based on the order of the matrix
If
$ CR $ (5) Aggregate priorities: Combine the priority weights through the hierarchy to determine the overall preferences of alternatives. For each alternative, calculate the weighted sum of criteria scores:
$ \text{Weighted Sum} = \sum\limits_{i = 1}^{n} \text{Criterion Score}_i \;\times\; \text{Priority Weight}_i $ Hierarchical framework for decision-making
-
In this research, we present a comprehensive hierarchical structure for our decision-making framework, aimed at systematically assessing and prioritizing strategies to enhance the resilience and reliability of different electricity grid landscapes in the face of diverse natural hazards. The framework addresses two primary research objectives: first, understanding how various electricity grid landscapes respond and interact with specific natural hazards, and second, utilizing a Multi-Criteria Decision-Making with Analytic Hierarchy Process (MCDM-AHP) to evaluate mitigation and adaptation strategies.
The first objective involves a hierarchical breakdown of electricity grid landscapes, categorizing them into centralized grids, microgrids, nanogrids, and smart grids. This is further dissected to explore responses to distinct natural hazards such as hurricanes, wildfires, earthquakes, floods, and extreme weather events. We delve into the implications for resilience and reliability by evaluating grid performance metrics, identifying vulnerabilities and strengths, and analyzing interdependencies among different landscape types and hazards.
For the second objective, we introduce a detailed breakdown of mitigation and adaptation strategies, encompassing site selection, redundancy, infrastructure hardening, emergency procedures, vegetation management, real-time monitoring, flexible operation, distributed generation, battery storage, demand response, community engagement, scenario planning, collaboration, climate-resilient technologies, regular maintenance, and artificial intelligence. These strategies are systematically evaluated based on multiple criteria, including effectiveness, resilience enhancement, risk reduction, scalability, flexibility, long-term sustainability, resource availability, cost-effectiveness, ease of implementation, integration with other strategies, community engagement, environmental impact, technological maturity, and regulatory and policy compliance, as well as education and training.
This hierarchical structure provides a systematic approach to analyzing the intricate interactions between electricity grid landscapes and natural hazards. Simultaneously, it facilitates the evaluation and prioritization of diverse mitigation and adaptation strategies based on a comprehensive set of criteria.
Elucidating interconnections among criteria, alternatives, and criteria–alternatives interactions
-
In the evaluation of mitigation and adaptation strategies for electricity grid landscapes in the face of natural hazards, it is imperative to clarify the intricate dependencies between the criteria, alternatives, and the interaction between criteria and alternatives. The Multi-Criteria Decision-Making with Analytic Hierarchy Process (MCDM-AHP) serves as a robust framework for systematically unraveling these dependencies.
The criteria are outlined in section Key Criteria, while section Key Strategies contains the presentation of strategies.
Dependencies between criteria
-
● Effectiveness, resilience enhancement, and risk reduction (C1): The efficacy of a strategy is closely tied to its impact on enhancing the resilience of the electricity grid. Strategies demonstrating higher effectiveness are expected to contribute more significantly to risk reduction and overall resilience enhancement.
● Scalability, flexibility, and long-Term sustainability (C2): The scalability and flexibility of a strategy are intertwined with its long-term sustainability. A strategy's ability to adapt to evolving circumstances is crucial for its long-term effectiveness and scalability.
● Resource availability, cost-effectiveness, and ease of implementation (C3): The availability of resources directly influences the cost-effectiveness and ease of implementation of a strategy. Striking a balance between these criteria is essential for practical and sustainable application.
● Integration with other strategies (C4): The success of a strategy may depend on its seamless integration with other mitigation and adaptation approaches. Identifying and leveraging synergies among strategies is critical for a holistic and effective grid resilience plan.
● Community engagement (C5): The level of community engagement is intertwined with the success of a strategy. Strategies that foster community involvement are likely to be more successful in implementation and garnering support.
Dependencies between alternatives
-
The alternatives, representing specific mitigation and adaptation strategies, exhibit dependencies based on their nature and scope. For instance, the integration of distributed generation (S8) may be closely related to the implementation of flexible operation strategies (S7).
Dependencies in criteria–alternatives interaction
-
● Environmental impact (C6): The environmental impact of a strategy is intimately linked to the choice of specific alternatives. Strategies incorporating climate-resilient technologies (S14) and artificial intelligence (S16) may have varying environmental footprints.
● Technological maturity (C7): The maturity of a technology (S14, S16) influences its feasibility and effectiveness. Assessing the technological maturity criteria is vital for understanding the practicality and potential success of specific strategies.
● Regulatory and policy compliance (C8): Strategies must align with existing regulations and policies. This criterion directly impacts the feasibility and acceptance of alternatives, emphasizing the need for careful consideration of legal frameworks.
● Education and training (C9): The successful implementation of certain strategies, such as real-time monitoring (S6) and artificial intelligence (S16), may be contingent on the level of education and training within the workforce.
Understanding these dependencies provides a nuanced perspective essential for the robust application of the MCDM-AHP framework. By elucidating the interconnections between criteria, alternatives, and their interactions, this research aims to enhance the clarity and efficacy of decision-making processes for resilient electricity grids.
Data collection and processing
-
While existing literature provided valuable insights into the broader aspects of electricity grid resilience and adaptation strategies, it often lacks the specificity required for our study's unique criteria and alternatives. To overcome this limitation, we meticulously executed our own objective judgment process, which involved a structured evaluation of criteria, alternatives, and their interrelationships. This approach drew upon both logical reasoning and the extensive knowledge base available in the literature.
Our objective judgment process was intentionally designed to ensure that assessments of criteria and alternatives adhered to a clear and consistent logic rooted in the domain knowledge found in the literature. This step was crucial in tailoring our analysis to the specific nuances of our study, aligning with the diverse range of criteria and alternatives we aimed to evaluate.
Next, the collected data underwent a rigorous pairwise comparison process. We utilized the Saaty scale, a widely accepted method within Analytic Hierarchy Process (AHP), to convert qualitative expert judgments into numerical values[52,53,55]. Eigenvalue calculations were employed to determine the consistency of expert judgments. Adjustments were made if necessary to enhance the reliability of the decision-making model (Table 1).
Table 1. Pairwise comparison matrix for criteria evaluation.
Criteria C1 C2 C3 C4 C5 C6 C7 C8 C9 C1 1 5 7 7 5 3 5 7 5 C2 $\dfrac{1}{5}$ 1 3 5 3 2 3 5 3 C3 $\dfrac{1}{7}$ $\dfrac{1}{3}$ 1 3 2 1 3 3 2 C4 $\dfrac{1}{7}$ $\dfrac{1}{5}$ $\dfrac{1}{3}$ 1 3 1 3 5 3 C5 $\dfrac{1}{5}$ $\dfrac{1}{3}$ $\dfrac{1}{2}$ $\dfrac{1}{3}$ 1 1 3 3 3 C6 $\dfrac{1}{3}$ $\dfrac{1}{2}$ 1 1 1 1 3 3 2 C7 $\dfrac{1}{5}$ $\dfrac{1}{3}$ $\dfrac{1}{3}$ $\dfrac{1}{3}$ $\dfrac{1}{3}$ $\dfrac{1}{3}$ 1 3 3 C8 $\dfrac{1}{7}$ $\dfrac{1}{5}$ $\dfrac{1}{3}$ $\dfrac{1}{5}$ $\dfrac{1}{3}$ $\dfrac{1}{3}$ $\dfrac{1}{5}$ 1 3 C9 $\dfrac{1}{5}$ $\dfrac{1}{3}$ $\dfrac{1}{2}$ $\dfrac{1}{3}$ $\dfrac{1}{3}$ $\dfrac{1}{2}$ $\dfrac{1}{3}$ $\dfrac{1}{3}$ 1 (C1) Effectiveness, resilience enhancement, and risk reduction; (C2) Scalability, flexibility, and long-term sustainability; (C3) Resource availability, cost-effectiveness, and ease of implementation; (C4) Integration with other existing or planned strategies; (C5) Community engagement and stakeholder acceptance; (C6) environmental impact; (C7) Technological maturity; (C8) Regulatory and policy compliance; (C9) education and training—when assessing strategies for mitigating and adapting to natural hazards in microgrids. We use a rating scale ranging from 1 to 9, where 1 indicates equal importance and 9 represents significantly greater importance. It's important to recognize that this assessment is subjective and may vary based on individual perspectives and preferences. Criteria and alternative weights were then aggregated to establish overall preference scores for each strategy. This comprehensive consideration involved accounting for all criteria and their associated weights. With the aggregated scores, we conducted a ranking of strategies to unveil their alignment with the objectives of our study, as represented by the overarching goal and specific criteria (Tables 2 & 3).
Table 2. Criterion weights (CWs) delineate the relative importance assigned to each criterion in the evaluation of strategies aimed at mitigating and adapting to natural hazards within microgrids. These weights provide clarity on the respective significance of each criterion in influencing the overall effectiveness of the available options.
Criteria Relative weights (RWs) Effectiveness, resilience enhancement, and risk reduction (C1) 28.1% Scalability, flexibility, and long-term sustainability (C2) 12.7% Resource availability, cost-effectiveness, and ease of implementation (C3) 7.8% Integration with other strategies (C4) 11.7% Community engagement (C5) 10.2% Environmental impact (C6) 6.0% Technological maturity (C7) 13.9% Regulatory and policy compliance (C8) 4.2% Education and training (C9) 5.3% Table 3. Combined weighted ratings for each alternative. Higher weighted sums indicate enhanced overall performance.
Alternatives Weighted sum Site selection 1.935 Redundancy 1.776 Hardening infrastructure 1.999 Emergency procedures 1.732 Vegetation management 0.899 Real-time monitoring 1.738 Flexible operations 1.780 Distributed generation 2.102 Battery storage 1.740 Demand response 1.963 Community engagement 1.531 Scenario planning 1.802 Collaboration 1.677 Climate-resilient technologies 1.743 Regular maintenance 1.522 Artificial intelligence 1.978 The choice of the Multi-Criteria Decision-Making with Analytic Hierarchy Process (MCDM-AHP) methodology for our analysis was deliberate, grounded in its capacity to effectively handle complex, multidimensional decision-making problems. AHP proved especially suitable for our study, given the interrelated nature of criteria, the existence of dependencies between criteria and alternatives, and the inherent need for subjective expert judgment. Its transparency and robustness made it an ideal choice, ensuring a thorough and insightful evaluation of mitigation and adaptation strategies in the context of natural hazards[52,53,55].
-
In this section, we embark on an in-depth exploration. First, we explore different types of electricity grids, including centralized grids, microgrids, nanogrids, and smart grids. Subsequently, we explore the different kinds of natural hazards that can affect microgrids. After that, we scrutinize a spectrum of strategies aimed at mitigating and adapting to these natural hazards within microgrids. We carefully consider the key factors that need to be evaluated when deciding on these strategies. Moreover, we shed light on the application of the Multi-Criteria Decision-Making (MCDM) methodology, specifically the Analytic Hierarchy Process (AHP). This approach systematically assesses both the criteria and strategies, thereby facilitating an informed decision-making process. The outcome is an enhanced natural hazards preparedness and response strategy that underpins effective decision-making.
Electricity grid landscapes: exploring centralized grids, microgrids, nanogrids, and smart grids
Centralized grid vs microgrids
-
A centralized grid, often referred to as the traditional or main grid, is a large-scale network managed by utility companies to generate, transmit, and distribute electricity to a wide geographic area, often spanning cities, regions, or even entire countries (left panel of Fig. 1)[63]. The centralized grid is centrally controlled by grid operators, who manage the flow of electricity, balance supply and demand, and ensure overall stability. Electricity is primarily generated at a few centralized power plants, often using non-renewable sources such as coal, natural gas, or nuclear power. Electricity is primarily generated at a few centralized power plants, often using non-renewable sources such as coal, natural gas, or nuclear power. Electricity is primarily generated at a few centralized power plants, often using non-renewable sources such as coal, natural gas, or nuclear power.
A microgrid is a localized energy system that can operate independently or in conjunction with the centralized grid[64]. It serves a specific area, such as a university campus, military base, industrial facility, or community[65, 66].
● Island mode operation: Microgrids can disconnect from the main electrical grid and operate in island mode during grid outages or emergencies. This provides a localized source of power and helps maintain critical services, such as hospitals or emergency response centers[67, 68].
● Grid-connected mode: Microgrids can also remain connected to the main grid while still managing their internal generation and consumption. This mode allows for sharing surplus energy with the main grid and earning revenue through energy trading or grid services[69, 70].
Microgrids can be controlled locally and can operate autonomously from the main grid if necessary, allowing them to respond to local energy needs and conditions. Communication protocols (e.g., Supervisory Control and Data Acquisition, or SCADA; Internet of Things, or IoT) facilitate data exchange between components and enable real-time monitoring and control[71, 72]. Microgrids often integrate a mix of distributed energy resources (DERs)[18,73], a decentralized energy technologies that generate, store, or manage energy closer to the point of consumption (e.g., solar photovoltaic panels, wind turbines, combined heat and power or CHP systems, backup diesel or natural gas generators, fuel cells, micro-gas turbines, biomass generators, small-scale hydroelectric generators, geothermal systems, demand response technologies, electric vehicle charging infrastructure, energy storage technologies[74, 75] such as batteries or hydrogen-based storage which can store excess energy generated during times of low demand and release it during peak demand periods or when renewable sources are not generating power[6,76], etc.). Electricity within a microgrid is generated, stored, and distributed locally, reducing the need for long-distance transmission. Electricity within a microgrid is generated, stored, and distributed locally, reducing the need for long-distance transmission. Fault detection and isolation systems and cybersecurity measures[50] ensure the safety and security of the microgrid’s components and operations. Microgrids are particularly useful in remote or isolated locations, critical infrastructure sites, and areas prone to natural disasters. They can also help optimize energy use, reduce carbon emissions, and lower electricity costs.
In summary, a centralized grid is a large-scale network managed by utilities for widespread electricity distribution, while a microgrid is a smaller, localized energy system that can operate independently or in conjunction with the centralized grid, offering increased resilience and flexibility[63] (Fig. 1).
Microgrid vs nanogrid vs smart grid
-
Microgrids and nanogrids are localized energy systems that provide more autonomy and resilience, while a smart grid is a modernized electricity grid that incorporates advanced communication and control technologies to monitor and manage the flow of electricity, optimizing the use of energy resources. In fact, a nanogrid is even smaller in scale than a microgrid, typically serving a single residential building or a small cluster of buildings and small-scale commercial facilities[77, 78]. Smart grids enable bidirectional communication between the utility and consumers, allowing for real-time data exchange and better demand-response management (i.e., allowing consumers to adjust their energy usage based on real-time pricing and availability)[79] (right panel of Fig. 1).
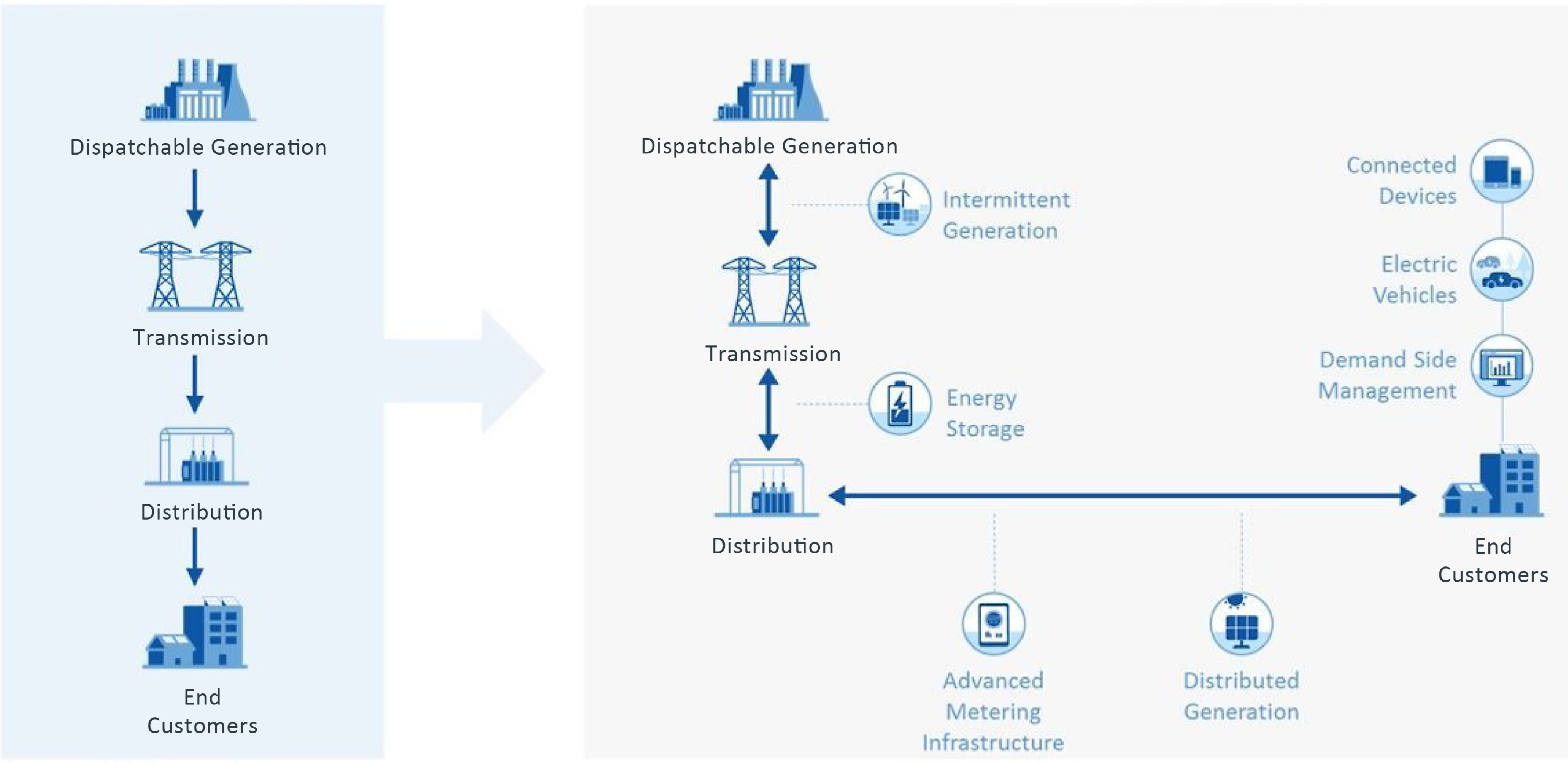
Figure 1.
Contrasting grid models: On the left, the traditional centralized electricity grid; on the right, the evolving decentralized grid showcasing microgrids, nanogrids, and smart grids[80].
Microgrid vulnerabilities: exploring the spectrum of natural hazards
-
Microgrids can be vulnerable to a variety of natural hazards that may impact their operation, reliability, and resilience. Some of the natural hazards that can affect microgrids include:
● Extreme weather events: Severe weather conditions such as hurricanes, tornadoes, blizzards, and heavy storms can damage physical infrastructure, disrupt energy generation, and cause power outages. Microgrids need to be designed and built to withstand these conditions[81, 82].
● Extreme temperatures: Extreme cold or heat[11, 12] (Fig. 2) can impact the performance of energy storage systems, batteries, and other components within a microgrid. Proper thermal management is essential to maintaining efficiency and reliability.
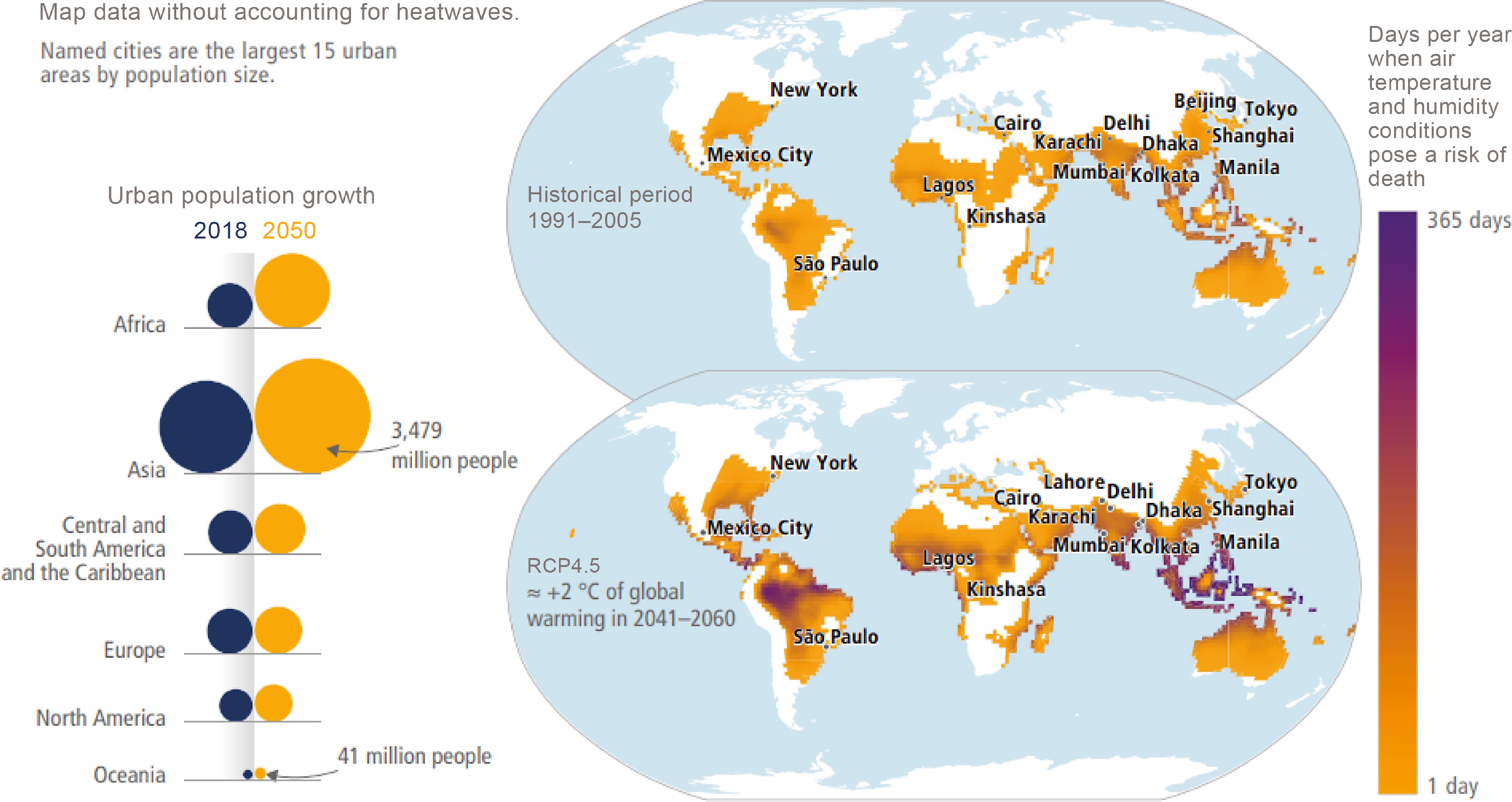
Figure 2.
Population exposed to lethal climatic conditions from extreme temperatures and humidity. The top panel depicts the historical era (1991–2005), while the bottom panel illustrates the RCP4.5 scenario (2041–2060) under 2 °C global warming. RCP (Representative Concentration Pathway) scenarios, utilized in conjunction with CMIP5 (Coupled Model Intercomparison Project Phase 5)[11], offer insights into potential climate impacts on societies[90].
● Floods: Flooding[11, 12] (Fig. 3) can damage equipment, submerge electrical components, and affect the overall functionality of a microgrid. Proper site selection, elevation, and flood-resistant design are essential to mitigate flood-related risks[83].
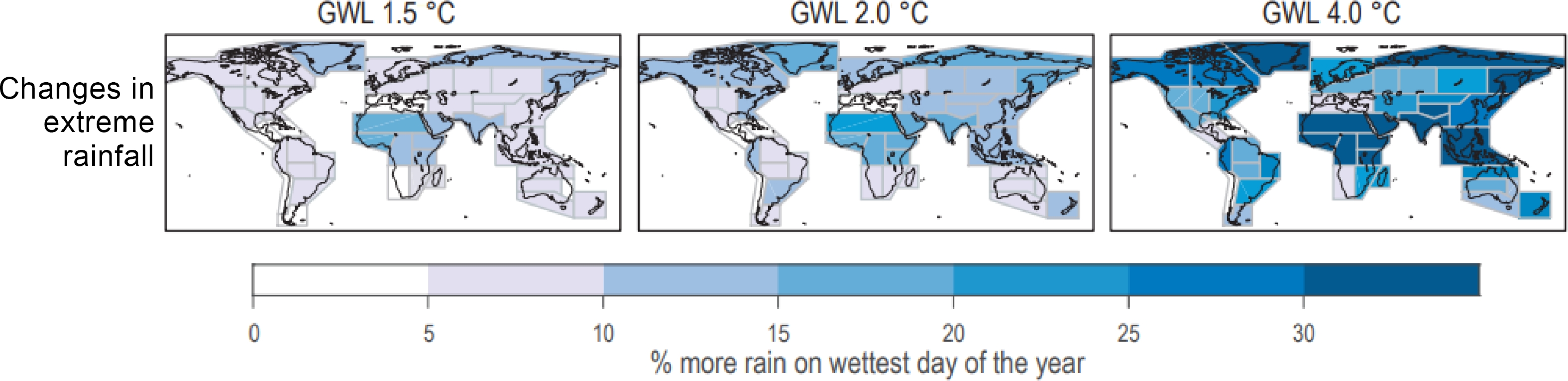
Figure 3.
Maps depicting CMIP6 (Coupled Model Intercomparison Project Phase 6) median projections of extreme rainfall changes across AR6 (6th Assessment Report) land regions at varying global warming levels (GWLs) of 1.5, 2, and 4 °C. It provides insights into potential future precipitation patterns in response to different warming scenarios[91].
● Wildfires: Microgrids located in areas prone to wildfires may face the risk of damage from flames, heat, and smoke[7, 8]. These hazards can impact energy generation, distribution infrastructure, and even the availability of fuel for backup generators[18,84].
● Earthquakes: Seismic activity can lead to structural damage and disruptions in power distribution. Microgrids in earthquake-prone regions need to be designed to withstand ground motion and potential aftershocks[15,85].
● Lightning strikes: Lightning can damage electrical equipment and disrupt power distribution. Adequate grounding and lightning protection measures are important for microgrid components[86].
● Tsunamis: Coastal microgrids are at risk of tsunamis, which can inundate the area and damage infrastructure, including energy generation and distribution facilities[87].
● Volcanic activity: Microgrids situated near active volcanoes may be exposed to volcanic ash, which can damage equipment and disrupt power generation and distribution[15,85].
● Landslides: Microgrids located in hilly or mountainous terrain may be susceptible to landslides, which can damage infrastructure and disrupt energy flow[88].
● Ice and snow accumulation: Cold climates with heavy snow and ice can lead to the accumulation of ice on equipment, power lines, and solar panels, affecting energy generation and distribution[89].
● Sea-level rise: Coastal microgrids may face risks from rising sea levels due to climate change (Fig. 4), which can lead to saltwater intrusion, flooding, and corrosion of equipment[42].
To enhance the resilience of microgrids against natural hazards, careful planning, design, and implementation are essential.
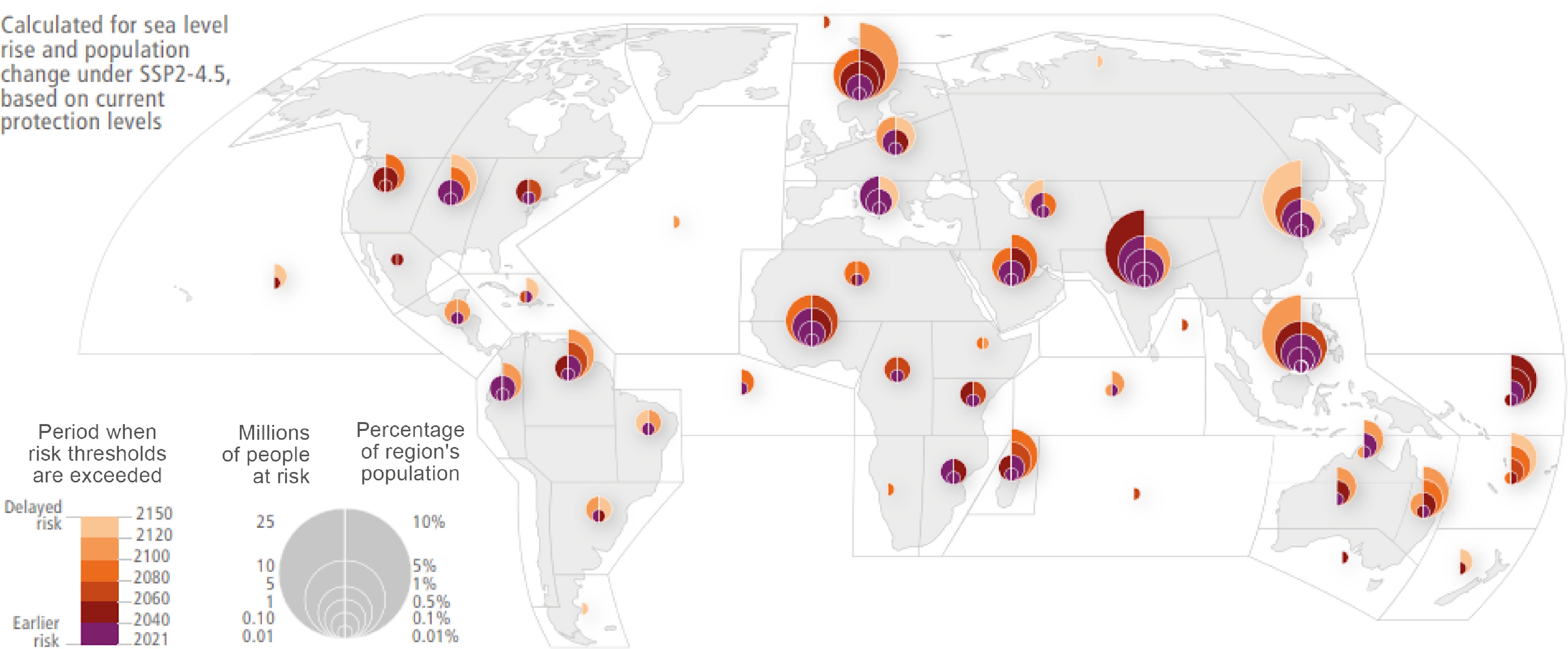
Figure 4.
Mapping future coastal flood risk (i.e., sea level rise): projected population vulnerability to a 100-year event, under the Shared Socioeconomic Pathway 2−4.5, which represents a scenario where the world takes moderate mitigation and adaptation efforts. The 4.5 indicates radiative forcing levels by the year 2100, measured in Watts per square meter. This scenario is used in conjunction with CMIP6 (Coupled Model Intercomparison Project Phase 6) climate models to explore potential climate outcomes and societal responses)[11,90].
Enhancing microgrid resilience: evaluating mitigation and adaptation strategies through MCDM-AHP analysis
Key strategies
-
Mitigating and adapting to natural hazards in microgrids involves a combination of proactive planning, engineering solutions, and operational strategies. Key strategies, including artificial intelligence, early warning systems, prediction techniques, and geospace observation, for addressing natural hazards in microgrids include:
Mitigation strategies
-
● Site selection: It consists of choosing microgrid sites that are less vulnerable to specific hazards, such as avoiding flood-prone areas, landslides, or areas prone to wildfires. Selecting an elevated location can reduce the risk of flooding and minimize potential water-related damage during heavy rains or storm surges. Opting for locations with stable geology and minimal seismic activity helps mitigate the risk of structural damage from earthquakes. Moreover, avoiding sites with dense vegetation can reduce the risk of wildfires affecting the microgrid infrastructure.
● Redundancy: Redundancy, in the context of microgrids and systems engineering, refers to the inclusion of duplicate or backup components, subsystems, or processes within a system. The primary purpose of redundancy is to enhance reliability and ensure that a system can continue to function properly even if certain components or elements fail due to various reasons, including natural hazards, technical failures, or other disruptions. For instance, incorporating multiple energy sources, such as solar panels, wind turbines, and backup generators, ensures that the microgrid can continue generating power even if one source is affected by a hazard. Having redundant energy storage systems, like batteries or capacitors, provides backup power during disruptions, preventing energy shortages. In addition, creating redundant pathways for energy distribution and transmission ensures that power can still reach consumers even if certain distribution lines are damaged.
● Hardening infrastructure: It consists of strengthening microgrid components against hazards by using durable materials, fire-resistant design, reinforcing structures, and adding protective coatings to minimize damage. For instance, using corrosion-resistant materials prevents degradation of components due to exposure to elements like moisture, saltwater, or chemicals.
● Emergency procedures: Establishing predefined emergency procedures allows for a swift and coordinated response by the microgrid operators and stakeholders, reducing the time it takes to address hazards and mitigate their impact. By knowing how to properly react to specific hazard scenarios, the microgrid can minimize risks to personnel, equipment, and the community.
● Vegetation management: It consists of implementing clear vegetation around microgrid infrastructure to reduce the accumulation of combustible materials, lowering the likelihood of ignition and the spread of wildfires.
Adaptation strategies
-
● Real-time monitoring: Consists of implementing advanced monitoring and control systems to detect and respond to changing conditions, allowing for timely adjustments to microgrid operations.
● Flexible operations: Involves designing microgrid systems to be flexible and adaptable, allowing for seamless switching between grid-connected and island modes based on hazard scenarios. In fact, flexible operation allows the microgrid to quickly switch to a safer operational mode (e.g., island mode), to dynamically shed non-essential loads, and to balance energy generation and consumption when potential hazards are detected.
● Distributed generation: Distributed generation reduces reliance on a single centralized energy source, minimizing the impact of hazards that may disrupt a single source. Distributed generation allows the microgrid to operate independently of the larger grid during grid failures caused by hazards, ensuring continued energy supply.
● Battery storage: Consists of using energy storage systems to provide backup power during outages and maintain continuous operation. For instance, energy stored in batteries can be used to shift energy consumption to times when renewable energy generation is high, reducing reliance on grid power and minimizing vulnerability to supply disruptions. Battery systems can also help stabilize voltage and frequency fluctuations caused by hazard-related disturbances, ensuring a consistent and high-quality power supply.
● Demand response: Consists of implementing demand response strategies to manage energy consumption during peak periods or when resources are limited. In fact, demand response allows microgrid operators to temporarily reduce non-essential energy consumption during peak demand or hazard events, ensuring that critical loads are prioritized (i.e., load shedding). Shifting energy consumption to times when renewable energy generation is high contributes to the efficient use of available resources and reduces dependence on fossil fuels.
● Community Engagement: Consists of educating and engaging the local community to promote awareness of hazards, preparedness measures, and emergency response protocols. Engaging the community can encourage residents to adopt energy-saving practices and adjust their behavior during hazard events, reducing overall energy demand.
● Scenario planning: It consists of developing hazard-specific scenarios and response plans to guide decision-making and ensure readiness for potential events.
● Collaboration: Consists of collaborating with local authorities, emergency services, and neighboring communities to enhance overall resilience and coordinate response efforts.
● Climate-resilient technologies: Refers to the use of specialized technologies and design approaches that are specifically designed to withstand the impacts of changing climate conditions. These technologies aim to adapt to long-term shifts in environmental patterns, including temperature changes, sea level rise, extreme weather events, and more. It should be noted that hardening infrastructure focuses on strengthening the physical components of a system to withstand immediate and localized hazards like storms, floods, fires, and earthquakes, while climate-resilient technologies address the broader and longer-term impacts of changing climate conditions on the system's functionality and durability.
● Regular maintenance: Consists of establishing a routine schedule of inspections, repairs, and upkeep of the microgrid infrastructure and components to ensure that microgrid components remain in optimal condition, reducing the risk of failure during hazardous events.
By combining these mitigation and adaptation strategies, microgrid operators and planners can enhance the resilience of their systems, minimize downtime, and continue providing reliable energy services even in the face of natural hazards.
Artificial intelligence (AI) can significantly contribute to the enhancement of microgrid resilience and responsiveness in the context of natural hazards. AI's potential contributions encompass various areas:
Mitigation strategies utilizing artificial intelligence
-
● Risk assessment and prediction: AI algorithms analyze historical data, weather patterns, and environmental conditions to predict the likelihood and severity of specific natural hazards. This predictive capability aids microgrid operators in proactive preparation.
● Early warning systems: AI-powered sensors and monitoring systems detect environmental changes linked to imminent hazards, enabling timely preventive actions and infrastructure protection.
● Adaptive control: AI-enabled control systems automatically adjust microgrid operations based on hazard predictions, optimizing energy storage, resource dispatch, and load prioritization.
● Dynamic load management: AI optimizes energy consumption and distribution during hazards, balancing loads and safeguarding critical services.
● Resource allocation: AI strategically allocates energy resources during hazard scenarios, ensuring essential facilities receive power while non-essential areas are temporarily powered down.
Adaptation strategies leveraging Artificial intelligence
-
● Resilient energy management: AI optimizes microgrid operation under changing conditions, ensuring energy generation and consumption patterns withstand natural hazard fluctuations.
● Demand response planning: AI predicts demand variations during hazards, enabling effective demand response strategies to manage energy consumption and reduce microgrid strain.
● Fault detection and diagnostics: AI monitors microgrid components for anomalies and faults, facilitating early detection and diagnosis of hazard-induced issues for prompt maintenance and reduced downtime.
● Dynamic reconfiguration: AI enables dynamic microgrid layout reconfiguration, adapting to energy source changes and load demands during and after hazard events.
● Energy storage optimization: AI manages energy storage systems, storing excess energy before hazards and releasing it during disruptions to ensure uninterrupted power supply.
● Communication and coordination: AI-powered communication systems facilitate component coordination, enabling seamless transitions between grid-connected and islanded modes during hazards.
● Scenario simulation: AI-driven simulations model various hazard scenarios, helping microgrid operators assess strategy effectiveness and optimize response plans.
By harnessing AI's capabilities, microgrid operators gain informed decision-making, rapid response to dynamic conditions, and resource optimization to mitigate natural hazard impacts. AI's data processing and real-time insights enhance microgrid adaptive capacity and overall resilience against unpredictable natural events.
Key criteria
-
When evaluating strategies for mitigating and adapting to natural hazards in microgrids, several key criteria can be considered. These criteria help microgrid operators and planners make informed decisions about which strategies to prioritize and implement. The criteria include:
(1) Effectiveness, resilience rnhancement, and risk reduction:
● Effectiveness: This criterion assesses how well a strategy achieves its intended goals in mitigating or adapting to hazards. It considers whether the strategy effectively addresses the specific challenges posed by natural hazards.
● Resilience enhancement: Evaluates how the strategy improves the microgrid's ability to withstand and recover from hazard events, ensuring continuity of essential services.
● Risk reduction: Measures the strategy's impact on reducing risks to human safety, microgrid infrastructure, and the environment.
(2) Scalability, flexibility, and long-term sustainability:
● Scalability: Considers whether the strategy can be adapted to microgrids of various sizes and configurations, accommodating different operational contexts.
● Flexibility: Examines the strategy's adaptability to different hazard types and changing conditions, allowing the microgrid to respond effectively to unforeseen challenges.
● Long-term sustainability: Assesses the durability and viability of the strategy over time, considering its ability to withstand evolving hazard patterns and changing microgrid needs.
(3) Resource availability, cost-effectiveness, and ease of implementation:
● Resource availability: Analyzes the availability of financial, technical, and human resources required to implement and maintain the strategy.
● Cost-effectiveness: Balances the costs of implementing the strategy against potential losses from hazard-related disruptions, considering the overall value added to the microgrid.
● Ease of implementation: Examines how easily the strategy can be integrated into the existing microgrid infrastructure and operational processes.
(4) Integration with other existing or planned strategies: Assesses how well the strategy aligns with and complements other strategies or technologies already in place or planned for the microgrid, ensuring harmonious operation.
(5) Community engagement and stakeholder acceptance:
● Community engagement: Considers involving local communities, authorities, and relevant stakeholders in the planning, implementation, and operation of the strategy to enhance overall hazard preparedness.
● Stakeholder acceptance: Evaluates the level of support and buy-in from microgrid operators, local communities, authorities, and other stakeholders.
(6) Environmental impact: Examines the potential positive or negative effects of the strategy on the environment, considering sustainability and ecosystem impact.
(7) Technological maturity: Assesses the readiness and reliability of the technology or approach associated with the strategy, considering its proven track record and maturity.
(8) Regulatory and policy compliance: Ensures that the strategy aligns with relevant regulations, standards, and policies related to microgrid operation, safety, and environmental protection.
(9) Education and training: Considers the level of education and training required for microgrid operators and personnel to effectively implement and manage the strategy.
By evaluating strategies against these criteria, microgrid operators can make informed decisions that optimize their microgrid's resilience, adaptability, and overall ability to mitigate and adapt to natural hazards.
Quantitative evaluation framework
-
In this section, we thoroughly analyze strategies aimed at mitigating and adapting to natural hazards in microgrids. These strategies are rigorously evaluated based on a predefined set of criteria. To facilitate this evaluation process, we construct a pairwise comparison matrix (refer to Table 1), enabling us to gauge the relative importance of each criterion in relation to others (as demonstrated in Table 2). Using these established relative weights, we then calculate cumulative weighted scores for each disaster management approach (see Table 3). This computation yields a comprehensive score that accounts for the pivotal role played by each criterion in the overall assessment.
Based on the calculated relative weights (Table 2), we find that:
● Effectiveness, resilience enhancement, and risk reduction (C1): This criterion holds the highest relative weight at 28.1%. It indicates that the overall success of strategies in mitigating and adapting to natural hazards heavily relies on their ability to enhance resilience, reduce risks, and effectively address the challenges posed by these hazards.
● Technological maturity (C7): With a relative weight of 13.9%, this criterion underscores the importance of employing mature and advanced technologies to ensure the robustness and efficacy of the strategies.
● Scalability, flexibility, and long-term sustainability (C2): At 12.7%, this criterion emphasizes the need for strategies that can be scaled up, adapted over time, and maintained sustainably to cater to changing circumstances and evolving hazards.
● Integration with other strategies (C4): With an 11.7% relative weight, this criterion highlights the significance of strategies that can seamlessly integrate with existing or planned approaches, creating a synergistic and comprehensive response to natural hazards.
● Community engagement (C5): At 10.2%, this criterion indicates the importance of involving the community and stakeholders in the process, recognizing their role in successful hazard mitigation and adaptation efforts.
● Resource availability, cost-effectiveness, and ease of implementation (C3): With a relative weight of 7.8%, this criterion suggests that while resource constraints, cost-effectiveness, and ease of implementation are important, they are relatively less influential compared to other factors.
● Education and training (C9): At 5.3%, this criterion signifies the value of education and training, but its lower weight indicates that while important, it is not as critical as other considerations.
● Environmental impact (C6): With a 6.0% relative weight, this criterion suggests that while environmental concerns are relevant, they are assigned a lower priority compared to other aspects.
● Regulatory and policy compliance (C8): At 4.2%, this criterion reflects the need for alignment with regulations and policies, but its lower weight suggests it plays a relatively smaller role in the assessment.
Based on the calculated sums of alternatives (strategies) (Table 3), we find that:
● Distributed generation: This alternative has the highest weighted sum of 2.102, indicating that it is considered a top-performing option with respect to the evaluated criteria. It is likely that distributed generation offers strong benefits across multiple criteria, contributing to its elevated overall performance.
● Demand response: With a weighted sum of 1.963, this alternative also demonstrates strong performance. Its effective ability to respond to varying demands and enhance overall resilience is likely contributing to its higher rating.
● Artificial intelligence: This alternative has a weighted sum of 1.978, indicating that its incorporation of AI technologies contributes to its robust performance across the evaluated criteria.
● Scenario planning: With a weighted sum of 1.802, this alternative is performing well across the criteria, although not as strongly as the high-weighted alternatives. It suggests that its ability to anticipate and plan for different scenarios contributes to its balanced performance.
● Hardening infrastructure: At a weighted sum of 1.999, this alternative exhibits solid overall performance, emphasizing the importance of fortifying the microgrid's infrastructure to enhance resilience.
● Collaboration: With a weighted sum of 1.677, this alternative indicates relatively lower overall performance compared to others. While collaboration is valuable, its contribution to the overall strategy might be perceived as less influential.
● Regular maintenance: This alternative has a weighted sum of 1.522, suggesting that while maintenance plays a role, it may not have as strong an impact on overall performance as other alternatives.
The calculated Consistency Ratio (CR) is approximately 0.773. Since the CR is below the commonly accepted threshold of 0.1, we can conclude that the judgments provided in the pairwise comparison matrix for the criteria are consistent.
-
In this section, our focus shifts towards a comprehensive exploration of the factors influencing the performance of various mitigation and adaptation strategies in response to natural hazards. Building upon the detailed analysis presented in the prior section, where we dissected the strategies against specific criteria, our objective now is to provide a deeper contextual understanding of why certain approaches outperform or underperform in designated criteria. Through this examination, we unravel the intricate dynamics that govern the effectiveness of strategies such as site selection, redundancy, real-time monitoring, and community engagement. Subsequently, we extrapolate from these findings to offer practical insights tailored for policymakers, energy planners, and practitioners. The practical implications underscore the nuanced decision-making required at each level, emphasizing the significance of informed choices in building resilient and reliable electricity grids amidst the challenges posed by diverse natural hazards.
As we strive to provide meaningful insights into how various electricity grid landscapes respond to natural hazards and apply MCDM-AHP for hazard mitigation and adaptation strategies, it is crucial to recognize specific limitations that may affect the interpretation and generalization of our findings. Identifying these constraints not only enhances transparency but also paves the way for future research and methodological refinement.
Analysis of mitigation and adaptation strategies in response to natural hazards
-
In evaluating the performance of various strategies for mitigating and adapting to natural hazards within different electricity grid landscapes, a comprehensive analysis reveals nuanced insights into their effectiveness. The Multi-Criteria Decision-Making Analytic Hierarchy Process (MCDM-AHP) was employed to assess these strategies based on a set of well-defined criteria.
Effectiveness, resilience enhancement, and risk reduction (C1)
-
Strategies S3 (hardening infrastructure), S6 (real-time monitoring), and S8 (distributed generation) consistently outperformed others in this criterion. Hardening infrastructure directly addresses vulnerabilities[92], real-time monitoring enhances situational awareness[93], and distributed generation ensures energy availability during disruptions[94].
Scalability, flexibility, and long-term sustainability (C2)
-
S7 (flexible operation) and S8 (distributed generation) exhibit superior scalability and flexibility[94]. Their adaptive nature allows for seamless integration into diverse grid landscapes, ensuring sustainability in the face of evolving natural hazards.
Resource availability, cost-effectiveness, and ease of implementation (C3)
-
S8 (distributed generation) stands out as a cost-effective and easily implementable solution. Although resource availability is crucial, the scalability and modular nature of distributed generation contribute to its economic feasibility[94].
Integration with other strategies (C4)
-
S1 (site selection) and S14 (climate-resilient technologies) demonstrate strong synergy with other strategies. Proper site selection sets the foundation for the integration of climate-resilient technologies, creating a robust and interconnected system[38, 40−42].
Community engagement (C5)
-
S11 (community engagement) emerges as pivotal for overall success. Its positive impact on community resilience and preparedness enhances the effectiveness of other strategies. In contrast, strategies lacking community involvement may face hurdles in adoption and success[95].
Environmental impact (C6)
-
S2 (redundancy), S8 (distributed generation), and S9 (battery storage) exhibit environmentally friendly characteristics. Redundancy minimizes environmental stress[96], while distributed generation and battery storage contribute to a cleaner and more sustainable energy landscape[76,94].
Technological maturity (C7):
-
S6 (real-time monitoring)[93], S8 (distributed generation)[94], and S16 (artificial intelligence)[97, 98] showcase advanced technological maturity. These strategies leverage cutting-edge technologies to enhance grid resilience and responsiveness.
Regulatory and policy compliance (C8)
-
S13 (collaboration)[99] and S14 (climate-resilient technologies)[100] align well with regulatory frameworks. Collaboration fosters a cooperative approach, while climate-resilient technologies often align with governmental policies aimed at sustainability and hazard resilience.
Education and training (C9)
-
S13 (collaboration)[99] and S15 (regular maintenance)[101] contribute to education and training initiatives. Collaboration facilitates knowledge exchange, and regular maintenance ensures a well-trained workforce, strengthening the overall resilience of the electricity grid.
In summary, the analysis underscores the importance of considering multiple criteria when evaluating strategies for natural hazard mitigation and adaptation. While certain strategies excel in specific criteria, a holistic approach that combines complementary measures is crucial for building resilient and reliable electricity grids in the face of diverse and dynamic challenges.
Practical implications for policymakers, energy planners, and practitioners
-
The research findings provide valuable insights into the dynamic relationship between different electricity grid landscapes and natural hazards, as well as the efficacy of mitigation and adaptation strategies. The practical implications of these findings are multifaceted, addressing key considerations for policymakers, energy planners, and practitioners involved in enhancing the resilience and reliability of electricity grids.
Policymakers
-
Policymakers play a pivotal role in shaping the regulatory landscape and establishing frameworks that govern the energy sector. The research underscores the following implications for policymakers:
● Diversification of grid types: Policymakers should consider promoting a diversified portfolio of grid types, including microgrids, nanogrids, and smart grids, to enhance overall resilience. Policies supporting the integration of these diverse grid architectures can provide a robust foundation for mitigating the impact of specific natural hazards.
● Incentivizing climate-resilient technologies: Policies should incentivize the adoption of climate-resilient technologies (S14) within electricity grids. This can foster innovation and technological advancements, promoting grid systems that are better equipped to withstand the increasing frequency and intensity of natural hazards.
● Community engagement initiatives: Encouraging and facilitating community engagement (S11) in the planning and decision-making processes is crucial. Policies should prioritize initiatives that empower local communities to actively participate in resilience-building efforts, recognizing the social dimension of electricity grid resilience.
● Regulatory flexibility: Regulatory frameworks need to be flexible and adaptive, allowing for the integration of emerging technologies such as artificial intelligence (S16) and distributed generation (S8). Policymakers should create an enabling environment that fosters experimentation and implementation of cutting-edge solutions.
Energy planners
-
Energy planners are instrumental in designing and implementing strategies to enhance grid resilience. The research findings have direct implications for their planning efforts:
● Holistic risk assessment: Energy planners should conduct comprehensive risk assessments that account for the specific vulnerabilities of different grid types to various natural hazards. This will enable the development of targeted strategies that address the unique challenges faced by centralized grids, microgrids, nanogrids, and smart grids.
● Prioritizing flexible and scalable solutions: Strategies emphasizing flexibility (S7) and scalability (C2) should be prioritized in planning efforts. This ensures that the electricity grid can adapt to changing conditions and scale efficiently to meet the demands imposed by natural disasters.
● Cross-sector collaboration: Collaboration (S13) should be actively promoted in planning processes, encouraging coordination among different sectors such as energy, emergency management, and environmental protection. Cross-sectoral collaboration enhances the effectiveness of resilience strategies and promotes a holistic approach to grid resilience.
Practitioners
-
Practitioners involved in the implementation and operation of electricity grids will find the following practical implications relevant:
● Training and skill development: Given the importance of education and training (C9), practitioners should invest in developing the necessary skills and expertise to implement and maintain climate-resilient technologies, real-time monitoring systems, and other advanced solutions.
● Regular maintenance protocols: Practitioners should prioritize regular maintenance (S15) of infrastructure to ensure its continued functionality. This is especially critical for hardening infrastructure (S3) and ensuring the longevity of climate-resilient technologies.
● Emergency response protocols: Robust emergency procedures (S4) should be established and regularly tested. Practitioners should be well-trained in responding to various natural hazards promptly, minimizing downtime and ensuring a swift recovery of the electricity grid.
● Community outreach initiatives: Practitioners should actively engage with local communities (S11) to raise awareness about the importance of grid resilience and to gather valuable insights from community members. Such outreach initiatives contribute to the success of community-centric resilience strategies.
In conclusion, the research findings offer actionable insights for stakeholders at different levels, providing a roadmap for policymakers, energy planners, and practitioners to enhance the resilience and reliability of electricity grids in the face of an increasingly unpredictable natural hazard landscape. Adopting a holistic and adaptive approach is key to building sustainable and robust energy systems for the future.
Comprehensive comparison of the findings with existing research
-
In this study, the MCDM-AHP methodology was employed to assess a wide array of strategies aimed at enhancing the resilience of electricity grids to a spectrum of natural hazards (extreme weather events, floods, wildfires, earthquakes, lightning strikes, extreme temperatures, tsunamis, volcanic activity, landslides, ice and snow accumulation, sea-level rise). The identified strategies encompassed site selection 'S1', redundancy 'S2', hardening infrastructure 'S3', emergency procedures 'S4', vegetation management 'S5', real-time monitoring 'S6', flexible operations 'S7', distributed generation 'S8', battery storage 'S9', demand response 'S10', community engagement 'S11', scenario planning 'S12', collaboration 'S13', climate-resilient technologies 'S14', regular maintenance 'S15', artificial intelligence 'S16'. These strategies were evaluated across multiple criteria, including effectiveness, resilience enhancement, and risk reduction 'C1'; scalability, flexibility, and long-term sustainability 'C2'; resource availability, cost-effectiveness, and ease of implementation 'C3'; integration with other existing or planned strategies 'C4'; community engagement and stakeholder acceptance 'C5'; environmental impact 'C6'; technological maturity 'C7'; regulatory and policy compliance 'C8'; education and training 'C9'.
Our comprehensive analysis, employing the MCDM-AHP methodology, reinforces and extends the existing body of research on mitigation and adaptation strategies for natural hazards in electricity grids, providing valuable insights for policymakers, researchers, and practitioners engaged in enhancing the resilience of electricity grids worldwide.
Komendantova et al.[102] focuses on the growing complexity of safeguarding the electricity transmission system, considering various trans-boundary risks, factors affecting vulnerability, changing grid architectures, and public sentiments regarding infrastructure upgrades. The research discusses best practices derived from European Commission-supported projects that address different stages of critical infrastructure risk reduction, including risk assessment, mitigation, and management. Specifically, the publication examines best practices related to the risk governance process, emphasizing assessment methodologies, communication between scientific research and practical implementation, and the involvement of stakeholders and public acceptance in the decision-making process.
Fernández et al.[103] explores the intersection of sustainability, city resilience, and training for environmentalists in the context of natural hazards (NH). The study addresses the importance of building resilient cities as outlined in the 2030 Agenda for Sustainable Development, specifically focusing on SDG-related goals. The research conducts two studies: one investigating the training of environmentalists using gamification, and the other assessing the potential of gamification in natural hazard analysis and management. The findings indicate that the proposed city model is a sustainable alternative, emphasizing the role of simulation in design and its contribution to resilience against natural hazards. Furthermore, the research deems the gamification and simulation approach successful in training environmentalists, highlighting their utility in fostering the necessary competences for addressing sustainability challenges.
Another research study[104] investigates the trust levels of urban and rural residents in grassroots-level institutions and examines how this trust influences community resilience to environmental change in China. The study focuses on the commitments and capacities of these institutions in managing natural hazards and coordinating community responses. Through semistructured interviews in both a megacity (Tianjin) and a remote village (Wolong), the research reveals that public confidence in grassroots-level institutions is limited due to resource and power constraints. Residents in Wolong generally recognize the commitment and role of these institutions in fostering community connections, while urban residents in Tianjin remain skeptical. Solidarity issues may explain this difference. The findings suggest implications for state-society cooperation and disaster risk comanagement in both urban and rural China.
Bouramdane[13] explores the complex relationship between climate change and the built environment in the context of increasing urbanization and climate concerns. The research covers various aspects, including the impacts of climate change on buildings and cities, quantification methodologies, adaptive strategies, disaster management, eco-centric design paradigms, and assessment metrics. The goal is to provide a comprehensive understanding of the challenges posed by climate change and to offer a roadmap for creating resilient urban landscapes. The article envisions a future where eco-design, climate resilience, and practical strategies come together to shape buildings and cities that are sustainable and resilient in the face of environmental uncertainties.
Another study by the same author[10] explores the challenges and vulnerabilities faced by smart cities in the context of rapid urbanization and technological progress. It focuses on disaster management strategies for smart cities, considering both cyber threats and extreme weather events. The research employs the Analytical Hierarchy Process (AHP), a Multi-Criteria Decision-Making methodology, to systematically evaluate and prioritize these strategies. The analysis identifies Resilience Enhancement and Communication Redundancy as crucial considerations, with other criteria such as Accuracy and Timeliness, Scalability and Adaptability, Cost-effectiveness, Ethical and Privacy Considerations, and Training and Skill Requirements playing supporting roles. The study prioritizes disaster management strategies for smart cities, emphasizing Citizen Engagement and Education, Early Warning Systems, and data analytics. Other strategies, including Integrated Communication Systems, Resilient Infrastructure Design, Drones and Robotics, Artificial Intelligence Algorithms, and IoT-enabled Sensors and Monitoring, are also assessed for their potential contributions. The research aims to guide stakeholders such as urban planners, policymakers, and disaster management professionals in enhancing smart city resilience and prioritizing strategies based on critical factors for effective disaster management in the 21st century.
Limitations and future directions
-
While our research endeavors to contribute valuable insights into the response of different electricity grid landscapes to natural hazards and the application of MCDM-AHP for hazard mitigation and adaptation strategies, it is essential to acknowledge certain limitations that may impact the interpretation and generalization of our findings. Identifying these limitations opens avenues for future research and refinement of our methodology.
Scope of natural hazards
-
Our study focuses on a selected set of natural hazards, including hurricanes, wildfires, earthquakes, floods, and extreme weather events. However, the dynamic nature of environmental risks may introduce additional hazards or variations that were not comprehensively covered. Future research could expand the scope to include emerging threats or region-specific challenges.
Generalization across grid types
-
While we have examined centralized grids, microgrids, nanogrids, and smart grids, the diversity within each category may lead to variations in resilience and reliability. Future studies could explore specific subtypes within these grid categories to provide a more nuanced understanding of their responses to natural hazards.
Simplified model assumptions
-
Our research involves certain assumptions and simplifications in modeling grid responses and employing the MCDM-AHP framework. These simplifications may not capture the full complexity of real-world scenarios. Future research could incorporate more sophisticated models and real-time data for a more accurate representation of grid behavior.
Lack of real-world testing
-
The evaluation of hazard mitigation and adaptation strategies using MCDM-AHP is based on theoretical considerations and expert opinions. A potential limitation lies in the absence of real-world testing and validation. Future research could integrate field experiments or case studies to validate the effectiveness of proposed strategies in practical scenarios.
Criteria weighting subjectivity
-
The assignment of weights to criteria in the MCDM-AHP process involves a level of subjectivity, relying on expert judgments. While efforts were made to ensure consistency through pairwise comparisons, the inherent subjectivity remains a limitation. Future research could explore advanced techniques or collaborative decision-making approaches to enhance the objectivity of criteria weighting.
Exploring the following future directions for this study, we aim to address the identified limitations and advance our research by delving into dynamic risk assessment models, incorporating advanced simulation techniques, fostering cross-disciplinary collaboration, engaging stakeholders, and embracing continuous monitoring for adaptive strategies.
Dynamic risk assessment
-
Future research could focus on developing dynamic risk assessment models that adapt to changing environmental conditions. This approach would enable a more responsive and real-time evaluation of grid landscapes' vulnerabilities to evolving natural hazards.
Advanced simulation models
-
Integrating advanced simulation models could enhance the accuracy of predicting grid responses to natural hazards. Incorporating data-driven and machine learning techniques would enable a more realistic representation of the intricate interactions between grid components and environmental factors.
Cross-disciplinary collaboration
-
Collaborative efforts between engineering, environmental science, and social science disciplines could yield a more comprehensive understanding of the socio-technical aspects influencing grid resilience. Examining the interconnectedness of infrastructure, communities, and regulatory frameworks could uncover novel insights.
Stakeholder engagement
-
Future research could involve increased stakeholder engagement, including utility providers, local communities, and policymakers. Integrating diverse perspectives can contribute to a more holistic evaluation of the social, economic, and governance dimensions of resilience and reliability.
Continuous monitoring and adaptive strategies
-
Implementing continuous monitoring systems and adaptive strategies that respond dynamically to changing environmental conditions can enhance the robustness of hazard mitigation and adaptation plans. Future studies could explore the integration of smart technologies for real-time decision support.
In conclusion, while our research provides a foundational understanding of grid responses and MCDM-AHP applications, acknowledging these limitations and exploring future directions will contribute to the ongoing discourse on enhancing the resilience and reliability of electricity grids in the face of natural hazards.
-
The modern world is becoming increasingly reliant on electricity grids to power essential functions and facilitate daily life. However, these grids are susceptible to a range of natural hazards that can disrupt power supply, endanger public safety, disrupt critical services, and cause significant economic losses. As the frequency and intensity of natural disasters rise due to climate change and other factors[105−107], it is imperative to enhance the resilience and preparedness of electricity grids, particularly microgrids, which play a pivotal role in ensuring energy security and continuity during adverse conditions[108].
Electricity grids come in various configurations, from centralized grids that serve large geographic areas to microgrids and nanogrids that provide localized energy distribution. Smart grids further introduce advanced technologies to optimize energy flow and enhance efficiency. Understanding the vulnerabilities and strengths of these grid types is crucial for effective disaster mitigation and response strategies.
This research is motivated by the urgent need to develop robust strategies that can safeguard microgrids against natural hazards. Microgrids, being smaller and more localized energy systems, have the potential to provide critical energy supplies during emergencies. However, their effectiveness hinges on the deployment of appropriate mitigation and adaptation measures.
Research questions and methodology
-
To address this pressing issue, this study employs the Multi-Criteria Decision-Making (MCDM) method, specifically the Analytic Hierarchy Process (AHP), as a systematic framework for evaluating a comprehensive set of strategies. By assessing these strategies against a diverse set of criteria, ranging from technical effectiveness and resilience enhancement to socio-economic and environmental considerations, a holistic understanding of their potential benefits and trade-offs can be achieved.
General findings
-
The analysis of relative weights highlights several key criteria crucial for evaluating strategies aimed at mitigating and adapting to natural hazards. Foremost among them is the criterion of 'Effectiveness, Resilience Enhancement, and Risk Reduction (C1)', which carries the highest weight of 28.1%. This underscores the paramount importance of strategies that can enhance resilience, reduce risks, and effectively address the challenges posed by natural hazards. Emphasizing the role of technology, the criterion of 'Technological Maturity (C7)' holds a weight of 13.9%, underscoring the significance of employing mature and advanced technologies to ensure the robustness and efficacy of the strategies. Equally vital are considerations of scalability, flexibility, and long-term sustainability, encapsulated in 'Scalability, Flexibility, and Long-Term Sustainability (C2)' with a weight of 12.7%, highlighting the need for adaptable and sustainable strategies. The criterion of 'Integration with Other Strategies (C4)' follows with an 11.7% relative weight, emphasizing the seamless incorporation of strategies with existing or planned approaches for a comprehensive response to natural hazards. Recognizing the pivotal role of community involvement, the criterion of 'Community Engagement (C5)' accounts for 10.2%, emphasizing the necessity of including community and stakeholder perspectives for successful hazard mitigation and adaptation efforts. While important, the factors of resource availability, cost-effectiveness, and ease of implementation ('Resource Availability, Cost-Effectiveness, and Ease of Implementation (C3)') are relatively less influential, carrying a weight of 7.8%. 'Education and training C9' hold value at 5.3%, though their significance is comparatively lower, while environmental concerns are noted but given less priority in the 'Environmental Impact (C6)' criterion, which has a weight of 6.0%. Lastly, the need for alignment with regulations and policies is acknowledged in the 'Regulatory and Policy Compliance (C8)' criterion, though its role in the assessment is relatively smaller, carrying a weight of 4.2%.
Based on the calculated sums of alternatives from the evaluation, several key findings emerge. 'Distributed Generation' emerges as the top-performing option with the highest weighted sum of 2.102, indicating its robust performance across evaluated criteria, likely due to its multifaceted benefits. 'Demand Response' follows closely with a weighted sum of 1.963, demonstrating strong performance attributed to its effective adaptation to demand fluctuations and resilience enhancement. 'Artificial Intelligence' achieves a weighted sum of 1.978, showcasing its proficient incorporation of AI technologies across criteria. 'Scenario Planning', while not as dominant as the top alternatives, still performs well with a weighted sum of 1.802, highlighting its ability to anticipate and prepare for diverse scenarios. 'Hardening Infrastructure' attains a respectable weighted sum of 1.999, underscoring the significance of infrastructure reinforcement for heightened resilience. 'Collaboration', with a weighted sum of 1.677, exhibits relatively lower overall performance, suggesting its importance might be comparatively less influential within the overall strategy. Finally, 'Regular Maintenance' holds a weighted sum of 1.522, indicating its contribution to performance, though potentially not as impactful as other alternatives.
Contributions to the field
-
This research makes significant contributions to the field by offering a comprehensive analysis of the responses of different electricity grid landscapes—centralized grids, microgrids, nanogrids, and smart grids—to a spectrum of natural hazards. The study not only advances our understanding of how these grid types interact with hurricanes, wildfires, earthquakes, floods, and extreme weather events but also sheds light on the implications for their resilience and reliability. Furthermore, the integration of the Multi-Criteria Decision-Making Analytic Hierarchy Process (MCDM-AHP) provides a rigorous framework for the evaluation of diverse mitigation and adaptation strategies, offering a nuanced understanding of their performance based on multiple criteria. By examining strategies such as site selection, real-time monitoring, community engagement, and climate-resilient technologies, this research contributes a practical and holistic perspective to the discourse on enhancing grid resilience. The findings not only identify top-performing options but also emphasize the intricate interplay of factors influencing their efficacy. This holistic approach is encapsulated in the elucidation of practical implications tailored for policymakers, energy planners, and practitioners, providing actionable insights for building resilient and reliable electricity grids in the face of an evolving natural hazard landscape.
Perspectives
-
The exploration of electricity grid landscapes and their susceptibility to natural hazards, as well as the application of the Multi-Criteria Decision-Making (MCDM) method using the Analytic Hierarchy Process (AHP) for evaluating strategies in microgrid resilience, opens promising perspectives for enhancing disaster preparedness and response. Firstly, a deeper investigation into the interplay between grid configurations and specific hazard vulnerabilities could unveil nuanced insights into optimizing grid designs and deployment strategies. Additionally, the integration of innovative technologies, such as Artificial Intelligence and climate-resilient solutions, could provide a cutting-edge approach to bolstering microgrid resilience. Further research avenues might delve into the dynamic interactions between various strategies, fostering synergy and uncovering novel hybrid approaches to address multiple criteria simultaneously. In parallel, a focus on stakeholder engagement and community-driven initiatives could elevate the inclusivity and acceptance of microgrid resilience strategies. Moreover, extending the MCDM-AHP methodology to encompass real-world case studies and empirical data could fortify the practical applicability of the approach, paving the way for informed decision-making in diverse microgrid contexts. As the energy landscape continues to evolve in response to both natural challenges and technological advancements, ongoing research could provide invaluable insights that propel the development of robust and adaptable microgrid solutions, fostering greater resilience and sustainability in the face of an uncertain future.
-
As the sole author of this article, I solely conceptualized, designed, and conducted the research, including data collection, analysis, and interpretation. I am responsible for the drafting and revision of the manuscript. The entire intellectual and creative content of this article, including the research design, methodology, and writing, is the result of my individual efforts.
-
The data used in this study, as well as the detailed methodology adapted, are comprehensively described in the methodology section of this article.
-
The publication of this research article in the journal of Emergency Management Science and Technology (EMST) was made possible without incurring Article Processing Charges (APCs). The author would like to express her appreciation to the editorial board and staff of EMST for their commitment to promoting open access and facilitating the sharing of knowledge within the academic community. The author appreciates the invitation and the opportunity to share her research and insights with the academic community and the readers of the Emergency Management Science and Technology (EMST) journal. Additionally, we extend our heartfelt thanks to the organizers and editorial team for generously waiving the publication fee for the year 2023. This support greatly contributes to the dissemination of knowledge and facilitates wider access to valuable research findings. The author also expresses heartfelt appreciation to the editorial office and the diligent reviewers for their perceptive feedback and thorough review, contributing significantly to the improved clarity of this article.
-
The author declares that there is no conflict of interest.
- Copyright: © 2024 by the author(s). Published by Maximum Academic Press on behalf of Nanjing Tech University. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
-
About this article
Cite this article
Bouramdane AA. 2024. Natural hazards in electricity grids: from landscape dynamics to optimal mitigation and adaptation approaches. Emergency Management Science and Technology 4: e007 doi: 10.48130/emst-0024-0003
Natural hazards in electricity grids: from landscape dynamics to optimal mitigation and adaptation approaches
- Received: 07 September 2023
- Revised: 23 January 2024
- Accepted: 18 February 2024
- Published online: 25 April 2024
Abstract: This article discusses the increasing significance of microgrids in fortifying electricity grid resilience amidst evolving global energy trends. The study employs the Multi-Criteria Decision-Making Analytic Hierarchy Process (MCDM-AHP) to assess strategies for mitigating and adapting to natural hazards, utilizing a purposeful and structured judgment process with pairwise comparisons and eigenvalue calculations to establish overall preference scores. The chosen methodology, MCDM-AHP, is highlighted for its effectiveness in handling complex, multidimensional decision-making challenges with interrelated criteria and dependencies, guided by subjective expert judgment. The analysis of relative weights underscores the utmost importance of effectiveness, resilience enhancement, and risk reduction while also highlighting the significance of technological maturity, scalability, flexibility, long-term sustainability, integration with other strategies, community engagement, resource availability, cost-effectiveness, ease of implementation, education and training, environmental impact, and regulatory and policy compliance in evaluating strategies for natural hazard mitigation and adaptation. 'Distributed Generation' emerges as the top-performing option, followed closely by 'Demand Response' and 'Artificial Intelligence', while 'Scenario Planning', 'Hardening Infrastructure', 'Collaboration', and 'Regular Maintenance' also demonstrate varying levels of effectiveness across evaluated criteria in the mitigation and adaptation of natural hazards. This research investigates the varied responses of electricity grid landscapes to natural hazards, utilizing MCDM-AHP to assess resilience strategies, providing insights into the strengths and weaknesses of different grid types, and offering a comprehensive framework for policymakers and practitioners to enhance energy system resilience and reliability.













