Building trust for traffic flow forecasting components in intelligent transportation systems via interpretable ensemble learning

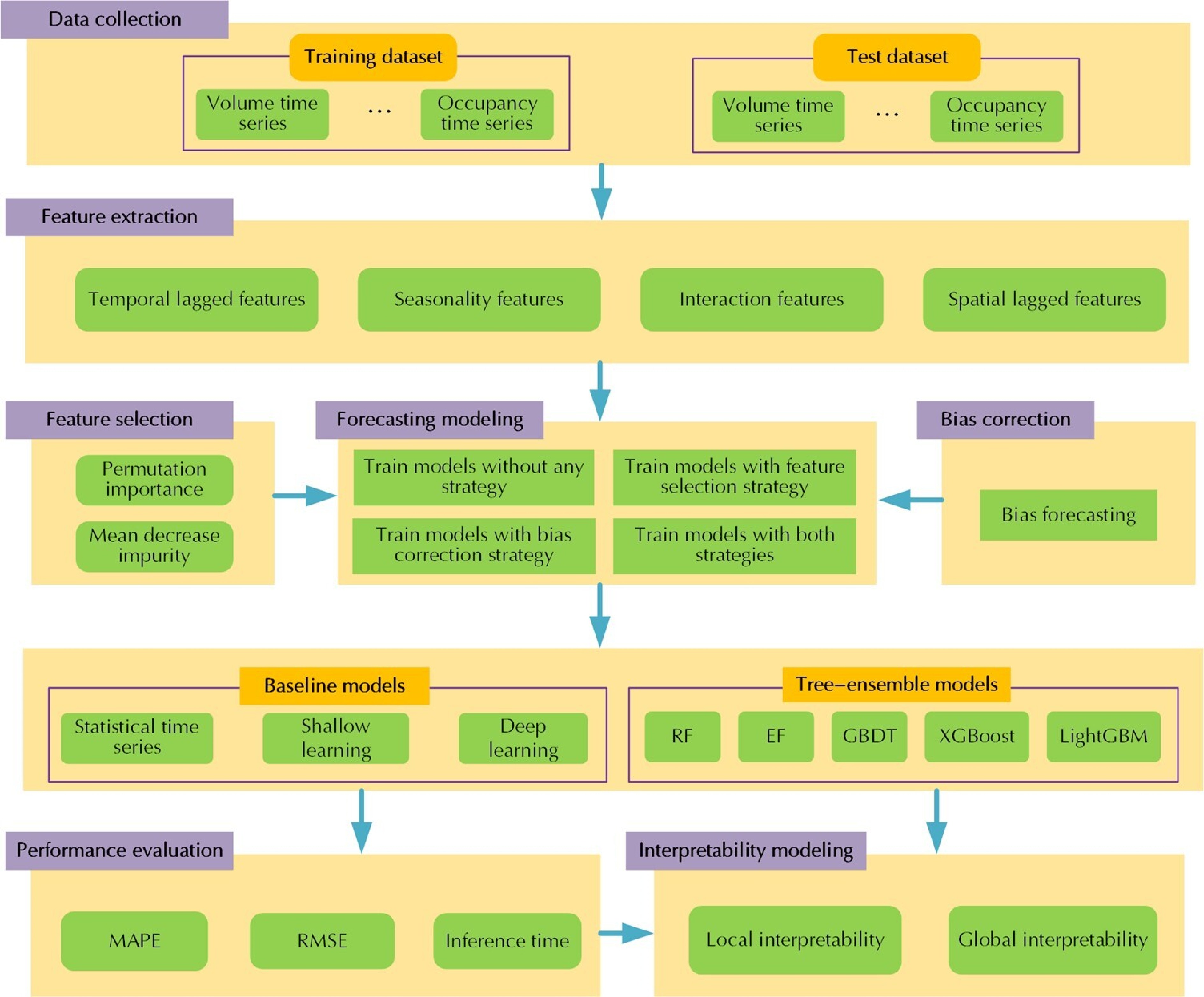
Intelligent transportation systems (ITSs) aim to promote service levels of various traffic facilities, mitigate traffic congestion, and reduce traffic accidents. As a crucial component of ITSs, traffic flow forecasting refers to mining underlying patterns from collected traffic flow measurements and using these patterns to infer future traffic conditions. Accurate, efficient, and trustworthy traffic flow forecasting can not only assist travelers in making reliable travel decisions but also help develop reliable proactive traffic management policies^[1,2].

Traffic flow forecasting has been a hot research topic over the past few decades. In the early stages, statistical time series methods were prevalent since they can effectively mine and utilize the autocorrelation underlying historical traffic flow data to produce future forecasts^[3]. These methods are based on solid statistical theory and are easy to understand. However, due to the linear assumptions and limited long-term forecasting capabilities, they struggle to capture the nonlinear patterns in traffic flow time series and hence lack sufficient accuracy and flexibility in congested situations. To overcome the above limitations, traditional machine learning methods were introduced to establish traffic flow forecasting models^[4]. These methods mainly employed shallow machine learning algorithms to learn complex correlations in traffic flow data and to further enhance their generalization ability. Nevertheless, due to the insufficient capability in handling large-scale data, it is often hard to achieve more significant performance using these methods than statistical time series methods. With the advent of the big data era, deep learning methods emerged as favored solutions in traffic flow forecasting^[5]. These methods can automatically extract representative features and complex patterns from massive datasets using an 'end-to-end' and 'deep' machine learning paradigm, demonstrating superior performance in modeling extensive and high-dimensional traffic flow data. It should be noted that deep learning methods typically aim to train complex models with a vast number of parameters and have often been criticized for their high computational cost and poor interpretability^[6].

It can be seen from the above analysis that most existing studies focused on developing cutting-edge algorithms or models to achieve state-of-the-art forecasting accuracy. Admittedly, accuracy is an extremely important metric in traffic flow forecasting. However, in real-life ITS applications, model accuracy alone is not sufficient. In practice, when forecasting models are deployed, it is inevitable that forecasting failures will occur during long-term operations. To ensure that failed models can recover quickly, traffic operators need to rapidly identify the cause of the failures and implement appropriate solutions based on this understanding. Consequently, interpretability plays a key role in traffic flow forecasting and should be treated as a crucial indicator when building such models. Additionally, to ensure timely model training and response, simple model tuning strategies and high inference efficiency are also necessary.

In the domain of machine learning, besides deep learning, ensemble learning is another powerful technique that can significantly enhance forecasting performance. Ensemble learning is an effective paradigm that improves model performance by combining multiple individual models^[7,8]. Recent studies^[9,10] have shown that ensemble learning methods can even outperform deep learning methods on specific tabular data. However, compared to deep learning, there is limited research on using ensemble learning for traffic flow forecasting, and its potential has not been fully explored. It is also important to note that while ensemble learning can improve the generalization ability of the overall model by combining multiple base models, its interpretability is often weakened due to the aggregated reasoning process involving thousands of decision rules^[11].

In this study, the aim is to develop an interpretable traffic flow forecasting framework based on ensemble learning and interpretable machine learning, where tree-ensemble algorithms are used to build forecasting models with strong generalization ability, while interpretable machine learning methods are employed to offer comprehensive model interpretability from multiple perspectives. To thoroughly explain the developed models, six categories of interpretable machine learning methods are employed, and interpretability analyses are conducted from both local and global perspectives. The consistency between daily traffic phenomena and the interpretability results, as well as the consistency among interpretations from different methods within the same category are examined across various scenarios using different traffic flow datasets. The forecasting models developed within this framework were compared with statistical time series models, shallow learning models, and deep learning models, demonstrating their potential in terms of accuracy, inference efficiency, and interpretability. In addition, the components of this framework can be tailored with various algorithms and tools, making it flexible and customizable for different application scenarios. The framework therefore offers a valuable alternative for developing reliable and trustworthy traffic flow forecasting components in ITS applications.

Traffic flow forecasting has been a hot topic over the past few decades. Early studies tried to develop traffic flow forecasting models using statistical time series methods, such as ARIMA^[12], SARIMA^[13], and various variants^[14,15]. Most of these time series models are linear, and they have two main issues. The first one is that these models often require some prior assumptions that are difficult to meet in practice. The other is that they struggle to capture nonlinear patterns underlying in traffic flow series. As a result, they are only able to produce reliable forecasts in stable traffic conditions.

To overcome the above drawbacks, researchers tried to use machine learning algorithms to build traffic flow forecasting models, given these algorithms show a brilliant ability to extract nonlinear, complicated traffic patterns. Machine learning is a popular branch of artificial intelligence (AI), and has been widely used in various transportation fields^[16−18]. For traffic flow forecasting, typical machine learning algorithms utilized include k-nearest neighbors^[19], support vector machine (SVM)^[20], and neural networks^[21]. Traffic flow forecasting models using machine learning algorithms can obtain satisfactory accuracy without requiring prior assumptions^[22].

The above studies focused on building a single forecasting model cannot exhibit an absolute advantage over various conditions resulting from complicated travel behaviors with irregular, stochastic characteristics^[23]. To further promote model accuracy, a few efforts have been made to improve single models by using ensemble learning techniques, a powerful machine learning technique that can enhance model accuracy and robustness by complimentarily leveraging the power of a set of single models. Wang et al.^[24] proposed a Bayesian combination method to enhance the accuracy of the developed traffic flow forecasting model, where the credit of each component predictor is determined by the prediction performance for a few intervals rather than for all intervals. Hou et al.^[25] showed that random forest can be used to establish a more accurate traffic flow forecasting model for planned work zone events. Along this line of work, Ou et al.^[26] developed an enhanced traffic flow forecasting model based on bias-corrected random forests and a data-driven feature selection strategy. Dong et al.^[27] utilized the wavelets decomposition technique and extreme gradient boosting (XGBoost) algorithm to construct the traffic flow forecasting model and demonstrated its superior performance compared with the SVM-based model. Weng et al.^[28] developed a novel traffic forecasting model based on XGBoost and a set of influencing factors to predict urban traffic operations, aiding in the design of effective strategies to alleviate traffic congestion. Lu et al.^[29] improved the model proposed by Ou et al.^[26] using a multi-regime modeling strategy.

The advancement of traffic detection techniques facilitates the collection process of traffic big data for traffic flow forecasting. Meanwhile, parallel computing techniques offer powerful computing power for big data mining. On this basis, a variety of deep learning models have been proposed for various applications. The success of deep learning lies in its 'end-to-end' learning paradigm and representation of learning ability that can be utilized to extract hierarchical, complicated features and nonlinear patterns^[5]. As a result, deep learning is applied to a variety of traffic flow forecasting tasks, including segment-wide forecasting and network-wide forecasting. Typical deep learning algorithms used in traffic flow forecasting include Deep Neural Network (DNN)^[30], Convolutional Neural Network (CNN)^[31], Recurrent Neural Network (RNN)^[32], Graph Neural Network (GNN)^[33−35], Attention-based Neural Network (A-NN)^[36], and Generative Adversarial Network (GAN)^[37,38]. The deep learning-based models can provide accurate forecasts when massive data is available. However, it is usually challenging for these models to obtain competitive performance when the size of the collected data is limited, while training deep learning models commonly need a high computational time and elegant hyper-parameter adjustment^[39]. In addition, the decision-making process of the models is often established as a 'black-box' and hence leads to insufficient interpretability^[40].

Interpretable traffic prediction

As deep learning and ensemble learning are the two most powerful techniques in traffic prediction, the interpretability problem associated with them deserves more attention in order to produce accurate and convincible forecasts for wide ITS applications. In the following section, the focus is on the existing studies on interpretable traffic prediction based on deep learning and ensemble learning.

Generally, deep learning models are built upon hundreds or even thousands of layers of neural networks. As the layers are interconnected with various linear and nonlinear transformations, the physical meanings of mappings from inputs to outputs for these models are unclear or difficult to understand^[40]. As a result, a few studies tried to explore interpretable deep learning models in traffic prediction. Wang et al.^[41] proposed a path-based deep learning framework for network-wide traffic speed prediction, where critical paths in the network are first identified and then utilized to reveal spatiotemporal feature interpretations by visualization and qualitative analysis. Wang et al.^[42] developed a deep polynomial neural network combined with a seasonal autoregressive integrated moving average model for short-term traffic flow forecasting. To improve model interpretability, the causality between historical spatiotemporal information and future traffic conditions is explicitly captured with a polynomial. Li et al.^[43] combined long short-term memory neural network and fuzzy system to develop a traffic volume prediction model, where the interpretability is enhanced by controlling the information flow with motivational factors. Wang et al.^[44] and Qin et al.^[45] introduced fuzzy cognitive maps to promote the interpretability of deep traffic prediction models. Ji et al.^[46] proposed a physics-guided traffic flow forecasting model, where a differential equation to describe the physical mechanism of traffic potential energy fields is established to introduce interpretability for the deep learning model. Given that GNN has great accuracy in spatiotemporal traffic prediction but exhibits an inability to explain the developed models, García-Sigüenza et al.^[47] and Tygesen et al.^[48] increased the transparency of the graph models with post hoc interpretability techniques.

There are several recent studies exploring the interpretability of traffic prediction models based on ensemble learning. Yang et al.^[49] developed a short-term traffic flow forecasting model based on GBDT and showed that the ensemble tree model can achieve good interpretability and high accuracy. Chikaraishi et al.^[50] compared ensemble models with deep learning models for short-term traffic prediction during disaster and concluded that the ensemble models produce more accurate results but less interpretability than the deep learning models. Zou et al.^[51] applied XGBoost to bus passenger flow prediction. In their study, the feature importance score was selected as the interpretability criterion. Fan et al.^[52] developed an interpretable machine learning model based on XGBoost to capture the complex interactions of urban variables and the main interaction effects on socio-economic statuses. Chen et al.^[53] established an interpretable model for tunnel geothermal disaster susceptibility evaluations based on ensemble learning and three interpretation methods, including permutation importance (PI), partial dependence plots (PDP), and the local interpretable model-agnostic explanations algorithm (LIME). Overall, these studies focus on using feature importance measures for model interpretability.

Summary

Most existing studies focused on developing cutting-edge algorithms or models to achieve state-of-the-art forecasting accuracy. However, in real-life ITS applications, model accuracy alone is not sufficient. To help traffic operators quickly identify the cause of model failures and implement appropriate solutions, the interpretability of traffic flow forecasting models must be carefully considered and demonstrated.

In the past decade, deep learning has been regarded as the most popular technique in traffic flow forecasting. Compared to deep learning, ensemble learning can also significantly enhance forecasting performance and therefore deserves more attention. Zhou & Feng^[39] argued that ensemble learning can be competitive with deep learning because of its excellent ability to well balance among data size, model performance (e.g., accuracy, robustness), and model training costs. Gorishniy et al.^[54] comprehensively compared deep learning models with ensemble learning models and discovered that there is no universally superior solution. Furthermore, a few recent studies^[9,10] proved that tree-ensemble models regularly outperform deep neural network models when handling tabular data. Pavlyuk^[55] and Manibardo et al.^[56] indicated that deep learning is not always the best answer for many traffic prediction tasks.

From the above analysis, it can be seen that tree-ensemble models can be an excellent choice for many traffic prediction tasks. It is also noteworthy that such models are usually composed of a large number of individual trees, meaning their reasoning process involves thousands of decision rules. As a result, gaining a full understanding of these models by simply examining each tree is infeasible. Although there have been recent efforts to enhance the interpretability of tree-ensemble models, they primarily used simple feature importance measures to explain the models, and cannot provide a comprehensive view of model behaviors or build sufficient trust for decision-makers.

To bridge the above gaps, the aim is to develop an interpretable traffic flow forecasting framework based on ensemble learning, and interpretable machine learning. Each core component of this framework is carefully designed to develop traffic flow forecasting models with competitive accuracy, high inference efficiency, and comprehensive interpretability.

Figure 1 provides the proposed interpretable traffic flow forecasting framework. The framework consists of seven key components, each of which is integrated into a comprehensive pipeline. In the following subsections, the details of feature extraction, feature selection, forecasting modeling, bias correction, and interpretability modeling will be illustrated.

Figure 1. 

The proposed interpretable traffic flow forecasting framework.

Feature extraction from traffic flow data

Extracting representative features from raw data is a crucial step in feature engineering for machine learning. Road traffic flows are influenced by various factors and typically exhibit distinctive characteristics and patterns. To capture these characteristics and patterns in traffic flow forecasting models, it is necessary to extract meaningful features. Recent studies^[57−59] have demonstrated that spatiotemporal relationships are vital for accurate traffic flow forecasting. Therefore, incorporating spatiotemporal relationships into feature extraction is critical. According to Ma et al.^[15], four categories of features were manually extracted from collected traffic flow data, including temporal lagged features, seasonality features, interaction features, and spatial lagged features. These extracted features were then used as input for the forecasting modeling component of the proposed framework and are described as follows.

Temporal lagged features

Temporal correlations underlying traffic flow data can be characterized by time-lagged features. The larger the lag order is, the more the lagged features are extracted. While more lagged features may yield higher model accuracy, the computation time for model training and inference can also increase.

Seasonality features

Traffic flow series commonly exhibits typical seasonal patterns. That is, the collected data may follow a daily cycle, a monthly cycle, or even an annual cycle. To capture the multi-seasonality, four seasonality features were extracted, including MinuteOfHour, HourOfDay, DayOfWeek, WeekOfMonth. Note that when massive data across years is available, other seasonality features such as MonthOfYear could also be extracted.

Interaction features

The fundamental diagram in traffic flow theory establishes a quantitative relationship among traffic volume, speed, and density. This relationship defines the dynamic interactions between traffic variables and can be leveraged to improve forecasting performance. Given this, the time-lagged features were extracted from multivariate traffic flow series as the interaction features. For example, the lagged occupancy or speed features could be extracted and used in forecasting traffic volume.

Spatial lagged features

In addition to temporal correlations, spatial correlations also exist in traffic flow data. For example, the upstream traffic flow at a specific location is likely to be affected by its downstream traffic. As a result, these spatial correlations are captured by extracting the temporal lagged features of multivariate traffic flow series at its neighboring sites, e.g., the upstream lagged volume features, the upstream lagged speed features, or the upstream lagged occupancy features, and so forth.

Other features that could be extracted include time-window statistical features, weather features, and road geometric features (e.g., the number of lanes, lane width, and road grade). When more useful features are available, the model performance could be further strengthened. Note that in this study, physically meaningful features are manually extracted. In practice, automatic feature extraction strategies^[39]could be employed to further enhance the diversity of the extracted features.

Feature selection for traffic flow forecasting

The extracted features described above may not contribute to the forecasts equally. Selecting proper features is therefore an essential step before forecasting modeling^[26]. Reliable feature selection can not only improve model performance but also enhance model efficiency. In this study, a simple empirical threshold strategy is developed to select proper features. The feature set composed of the selected features, F is determined by Eqn (1).

In the above equation, x^j is the j-th extracted feature, $ \varphi \text{(}{x}^{j}\text{)} $ is the feature importance of the j-th feature, $ \theta $ is the setting threshold of the feature importance, and M_E is the total number of the extracted features. Note that a few advanced feature selection strategies could be incorporated to seek better features.

Traffic flow forecasting modeling

In the following subsections, how to establish traffic flow forecasting models based on a single regression tree is described and the procedure of constructing ensemble forecasting models by combining multiple regression trees is further elaborated.

Forecasting with a single regression tree

Given the training data set D_train = {(x₁, y₁), (x₂, y₂), ..., (x_i, y_i), ..., (x_n, y_n)} with M_F selected features from F, where $ {x}_{i}\in {\mathbb{R}}^{{M}_{\mathrm{F}}} $ and $ {y}_{i}\in \mathbb{R} $ are the predicted feature vector and its associated forecast (target) of the i-th (1 ≤ i ≤ n) instance (data record), and $ n $ is the number of instances in D_train, the modeling procedure of the traffic flow forecasting with a single regression tree consists of the following four steps.

Step 1: Split D_train with the most informative feature and its splitting value. The most informative feature and its splitting value is defined as the splitting point, which can be determined by using an impurity metric to quantify its informative degree:

where, m and s are the index and value of the splitting feature. Not that the original feature space of D_train is segmented into two different subspaces R₁ and R₂ using the splitting point, and C₁, C₂ are the corresponding forecast average of the instances in R₁ and R₂, respectively.

Step 2: Based on the split results, we can compute the forecasts for each branch of the tree using Eqns (3) and (4).

In the above equations, R₁ and R₂ are the obtained subspaces, f_r is the forecast of the r-th branch.

Step 3: Repeat Step 1 and Step 2 until the stopping criterion (e.g., the maximum tree depth or the minimum instances at a leaf node meets the current condition) is reached.

Step 4: Based on the finally obtained subspace set {R₁, R₂, ..., R_k}, the forecasting model can be established as:

where, K is the number of leaves of the tree, R_k is the segmented k-th feature subspace, f_k is the forecast associated with R_k and I(x, R_k) is an indicator function, where returns 1 if $ x\in {R}_{k} $ and 0, otherwise.

Forecasting based on ensemble regression trees

Given the training data set D_train = {(x₁, y₁), (x₂, y₂), ..., (x_i, y_i), ..., (x_n, y_n)}, the developing process of the traffic flow forecasting model with ensemble regression trees is as follows:

Step 1: Build base forecasting models using a certain tree construction strategy

Two typical kinds of strategies can be used to construct base forecasting models, including sequential and parallel strategies. The sequential strategy tries to construct each base tree by considering the training error of its previous tree. In other words, there is a strong dependency relationship between the generated base trees. In contrast, the parallel strategy refers to constructing base trees independent of each other.

Note that no matter which kind of strategy is used, the training process of the base trees is the same as that of a single tree defined above. The main difference lies in that the base trees are trained with a new training data set D_gen, while the single tree directly used for traffic flow forecasting is constructed with a complete training data set D_gen. D_train canbe generated using some random sampling techniques. Generally, we can randomly sample instances or feature sets to obtain D_gen.

In this study, five popular tree-ensemble algorithms, including RF, EF, GBDT, XGBoost, and LightGBM, are introduced to build traffic flow forecasting models. Among them, the first three algorithms use the sequential tree construction strategy, while the other two algorithms adopt the parallel tree construction strategy.

Step 2: Build the ensemble forecasting model with a certain combination strategy

Given T base tree models $ {\left\{{Tree}_{t}\left(x\right)\right\}}_{t=1}^{T} $, the tree-ensemble model for traffic flow forecasting can be established using the following combination strategy:

In the above equation, α_t is the weight of the t-th base tree, $ \hat{f}\left(x\right) $ is the traffic flow forecasting model based on ensemble trees. The weight of each tree model can be determined using different strategies in different ensemble algorithms. For example, GBDT determines the weight as the training error of each base tree, while the weight is treated as 1/T in RF.

Forecasting performance improvement via bias correction

Bias correction is an effective strategy for improving the performance of tree-ensemble models^[26,29]. The output of the developed model by Eqn (6) is essentially the forecasted mean. By subtracting the forecasted mean from the actual target values in the training datasets, the forecasting biases can be obtained, which can be further harnessed to train a bias forecasting model. For the given instance $ x $, the output of the bias-corrected model is defined as the sum of the output of the mean forecasting model and the output of the bias forecasting model, as depicted by Eqn (7):

Explaining tree-ensemble models via interpretable machine learning

Interpretable machine learning has garnered extensive attention in recent years. A variety of interpretability methods have been proposed to effectively explain various machine learning algorithms^[6]. In this study, six categories of interpretable machine learning methods are introduced to provide a comprehensive explanation of the developed tree-ensemble models, covering both local and global perspectives. The local interpretability methods aim to answer why did the model make a certain prediction for a particular instance. In contrast, the global interpretability methods describe the average behavior of the developed model and explain model decisions by analyzing conditional interactions between features and forecasts on the whole dataset.

Local interpretability methods

Method A: Decision Paths

For a specific prediction from a regression tree, there exists a decision path from the root node to the leaf node. The decision path consists of a series of decisions guarded by a set of decision features. For a given instance x_i, we can quantify the contribution of each feature to the final prediction made by a tree model Tree_t(x_i) by building a decision path described by Eqn (8). Further, the final prediction from a tree-ensemble model can be decomposed to the predictions from multiple regression trees and described with an aggregated decision path, as shown in Eqn (9).

In the above equations, c_t is the bias and equals the value at the root node of the t-th tree (i.e., the mean value of the targets in the training data used by the t-th tree), $ {\xi }_{t}\left(x,j\right) $ is the contribution from the j-th feature in the feature vector x associated with the t-th tree. We can estimate $ {\xi }_{t}\left(x,j\right) $ as the prediction difference before and after splitting with the j-th feature along the decision path made by the t-th tree. According to the right part of Eqn (9), the importance of each feature when making a prediction with the feature vector x can be easily quantified.

Method B: Individual Conditional Expectation (ICE)

The method explains the model by using an ICE plot which depicts how the prediction of an individual instance changes as the interested feature value changes. ICE quantifies the dependence of the prediction on the interested feature for each instance. The dependence is estimated by keeping all other features the same, creating variants of the instance by replacing the interested feature's value with values from a grid, and making predictions with the trained model for these newly created instances. The result is a set of points for an instance with the interested feature value from the grid and the associated predictions.

Formally, given an instance $ {x}_{i}=\left({x}_{i}^{G},{x}_{i}^{C}\right) $, where $ {x}_{i}^{G} $ and $ {x}_{i}^{C} $ are the interested and the other features used in the traffic flow forecasting model $ \hat{f} $, the ICE can be estimated based on partial dependence function:

where, X^G represents the features to be explained and X^C represents the remaining features used in $ \hat{f} $ and are treated as random variables. Once the partial dependence of $ {x}_{i}^{G} $ on the prediction is quantified, the ICE plot can be made to visually explain the forecasting model by computing the forecasting curve $ \hat{{f}_{G}} $ against $ {x}_{i}^{G} $ that is determined with a series of split grids in the plot while making $ {x}_{i}^{C} $ fixed.

Method C: SHapley Additive exPlanations (SHAP)

The method aims to explain traffic flow forecasting models by quantifying the contribution of each feature to the prediction for a given instance. It achieves the goal by computing Shapley values^[60] based on coalitional game theory, where the feature values of the given instance act as players in a coalition and the prediction is treated as the payout. The features with larger absolute Shapley values are considered more important. Notably, feature contributions can be positive or negative, corresponding to the positive or negative 'pull effect' of the features on the prediction of the instance. Mathematically, the Shapley value of the j-th feature of instance x_i is defined as:

In the above equations, $ S $ is a subset of the features used in forecasting instance x_i which is the vector of feature values to be explained, $ {v}_{{x}_{i}}\left(S\right) $ is the prediction for feature values in $ S $ associated with instance x_i that are marginalized over features not included in S.

The Shapley value is suitable for any machine-learning model. However, the precise estimation of the Shapley value is commonly nontrivial. Given this, Lundberg & Lee^[61] proposed the SHAP approach inspired by local surrogate models to enhance the estimation of the Shapley values. SHAP belongs to a kind of additive feature attribution methods. That is, the prediction for instance x_i is equal to the average of all predictions in the whole dataset pluses the sum of all feature contributions associated with the instance, as illustrated by Eqn (13).

Given estimating the Shapley values requires numeric possible coalitions of the feature values and repeat simulation of the absence of a feature by drawing random instances, the TreeSHAP algorithm^[62] that extends SHAP and is capable of efficiently and precisely estimating the Shapley values for tree models are adopted in this study to explain the developed tree-ensemble traffic flow forecasting models.

Global interpretability methods

Method D: Global Feature Importance

For the tree-ensemble models developed in this study, three global feature importance measures are employed to quantify the importance of each feature from a global perspective.

D1: Permutation Importance. When building a base tree, the technique of bootstrap sampling with replacement is used to generate the training data set. In this situation, about one-third of the whole instances, called OOB samples, would not be drawn. OOB error is then defined as the mean prediction error of base trees on their associated OOB samples. Denote ErrOOB_t as the OOB error of the t-th tree, $ {Err\text{OOB}}_{t}^{j} $ as the OOB error of the t-th tree after randomly permuting the values of the j-th feature, the permutation importance associated with the j-th feature is calculated as:

As observed from the above equation, the larger the OOB error increases, the more important the feature is.

D2: Mean Decrease Impurity. The feature importance measure is defined as the average decreased impurity or gain caused by using a particular feature as the splitting feature across all trees, as shown in Eqns (15) and (16).

In the above equations, $ {\phi }_{\mathrm{M}\mathrm{D}\mathrm{I}}\text{(}{X}^{j}\text{)} $ represents the mean decreased impurity associated with the j-th feature across all trees, J_t(X_j) represents mean decreased impurity associated with the j-th feature in the t-th tree, and Q_t(Xⁱ = X^j) represents the variance reduction in the t-th tree caused by using the j-th feature as the l-th splitting node, and L_t is the number of the splitting nodes in the t-th tree. When $ {\phi }_{\mathrm{M}\mathrm{D}\mathrm{I}} $ of a feature is large, it is treated as a more informative feature.

D3: SHAP Feature Importance. The Shapley values can be used to measure the contribution of each feature for each instance. That is, the features with large absolute Shapley values are treated as more informative. The SHAP feature importance measure is estimated as the absolute Shapley values per feature across the whole dataset, as defined by Eqn (17).

In the above equation, $ {\phi }_{i}^{j} $ represents the Shapley value of the j-th feature associated with the i-th instance. The above measure quantifies the global importance of each feature on the whole dataset.

Method E: Feature Dependence

The method considers all instances in the dataset and measures the global relationship of a feature with the predicted outcome. Two categories of schemes can be adopted to explain feature dependence from a global perspective. The first is partial feature dependence and the other is SHAP feature dependence. The partial feature dependence scheme describes the function relationship between the features we are interested in and the predictions by marginalizing the model output over the distribution of the remaining features. The partial dependence function is defined by Eqn (10) and can be estimated by the Monte Carlo method, as illustrated by Eqn (18).

The above equation tells what the average marginal effect of the given features X^G on the forecast is. The partial feature dependence can be visually depicted using a partial dependence plot (PDP). The SHAP feature dependence scheme can also be used to check the average effects of the given features. Different from the partial feature dependence, the SHAP feature dependence considers the marginal effect of the interested features on the Shapley values rather than the predictions. That is, for instance x_i, the relationship between $ {x}_{i}^{j} $ and $ {\phi }_{i}^{j} $ would be considered. The SHAP dependence plot can be utilized to visually describe the SHAP feature dependence scheme.

Method F: Feature Interaction Effect

The feature interaction effect method can be used to explain the interaction effect between different features on the predicted outcome. Partial feature interaction effect and SHAP feature interaction effect are two typical methods. The 2D partial dependent plot can be used to visually check the feature interaction effect after quantifying the partial dependence using Eqn (18).

The SHAP feature interaction effect is the extra combined feature effect after accounting for the individual feature effects, and can be explained with the Shapley interaction index from game theory:

when $ i\ne j $:

The above two equations quantify the pure interaction effect after accounting for the individual effects by subtracting the main effect of the features. The SHAP dependence plot combined with the Shapley interaction index can be used to visually inspect the feature interaction effects for the given dataset.

To evaluate the proposed interpretable traffic flow forecasting framework, three traffic flow datasets were collected from different types of roads in China and the USA. The associated data information can be seen in Table 1. Specifically, the traffic flow dataset from a typical arterial of Kunshan, China, covers a period of 4 weeks from August 28 to September 24, 2012, with data aggregated at 5-min intervals. The traffic flow dataset from an expressway in Beijing, China, covers a period of 8 weeks from September 1 to October 26, 2009, with data aggregated at 2-min intervals. The traffic flow dataset from a freeway in Seattle, USA, covers 12 weeks from September 1 to November 23, 2015, with data aggregated at 5-min intervals.

For each dataset, the ratio of training instances to test instances is set to 3:1. All comparative models were implemented for one-step-ahead forecasting. The traffic flow variables consist of volume and occupancy. For arterial and freeway roads, the forecasting task is to predict the future volume of a target location using historical volume and occupancy data from the target location as well as its upstream and downstream locations. For the expressway road, the forecasting task is to predict the future volume of a target lane using historical volume and occupancy data from the target lane as well as its neighbor lanes. The maximum lag order in the feature extraction process is chosen as 4, 5, 4 for the three datasets, respectively.

Performance evaluation

Performance measure

To compare the performance of the developed models, two typical performance measures are adopted, defined as follows:

In the above equations, y_i and $ {\hat{y}}_{i} $ are the observed and forecasted values of the target variable, respectively, and n is the total number of traffic flow instances.

Experimental settings

In the present study, four typical categories of traffic flow forecasting models were implemented and compared, including statistical time series, shallow learning, deep learning, and ensemble learning. Table 2 lists the implemented traffic flow forecasting models.

For each model, several hyperparameters need to be tuned. With this in mind, some hyperparameter tuning strategies were adopted to select the proper model for evaluation. For the statistical time series model, the strategy proposed by Hyndman & Khandakar^[67] was employed to determine the optimal hyperparameters. For the shallow learning models and ensemble learning models, the grid search strategy based on time series cross-validation was adopted. For the deep learning models, the automated machine learning strategy developed in PaddlePaddle^[68] was utilized. The hyperparameter description for the developed models can be found in Supplemental Table S1. The selected hyperparameters for the evaluation of the developed models can be found in Supplemental Table S2.

Performance comparison

To conduct a comprehensive performance comparison, the MAPE and RMSE of the developed models on the three experimental datasets were respectively calculated, as listed in Table 3.

As observed from Table 3, the following insights can be drawn:

(1) For the arterial dataset, the ensemble learning models show better performance than the other three kinds of models. Within the shallow learning models, KNN outperforms the other models. Within the deep learning models, Transformer shows a clear advantage over other models in terms of the RMSE, while NBEATS performs the best in terms of MAPE. Within the ensemble learning models, RF and EF possess more performance advantage.

(2) For the expressway dataset, ensemble learning exhibits better performance in terms of RMSE, while deep learning performs the best in terms of MAPE. Within deep learning models, NBEATS still demonstrates the overall best performance, while LightGBM performs the best within the ensemble learning models.

(3) For the freeway dataset, the ensemble learning models significantly outperform the other three kinds of models. More specifically, GBDT performs the best in terms of RMSE, while RF outperforms other models in terms of MAPE.

(4) In summary, apart from the superior performance of deep learning on the expressway in terms of MAPE, ensemble learning demonstrates consistently superior performance.

In addition to model accuracy, model efficiency is another significant measure for traffic flow forecasting. Given this, the computational time of the developed models on the test datasets were recorded. The test time is presented in Table 4. As can be seen from the table, the statistical time series models, shallow learning models, and ensemble learning models show a similar computational time on the test dataset, with a significant efficiency advantage over the deep learning models. Overall, the ensemble learning models can combine accuracy, and efficiency advantages.

Bias correction and feature selection for enhancing tree-ensemble models

Bias correction and feature selection are two effective strategies commonly used to enhance the performance of tree-based models^[26]. The feature selection strategy improves model performance by eliminating redundant or irrelevant features and retaining those most informative. The bias correction strategy enhances model performance by training a separate bias forecasting model and adding the forecasting biases to the forecasting mean value.

To further check the forecasting capacity of the tree-ensemble models, the tree-ensemble models were implemented based on bias correction and/or feature selection and model performance inspected after applying these two strategies. The performance of the tree-ensemble models based on the bias correction strategy alone can be observed in Table 5. The performance of the tree-ensemble models based on the simple feature selection strategy alone can be seen in Table 6. The performance of the tree-ensemble models using both strategies can be seen in Table 7. In the above figures, the red arrow represents the model errors increase after using the given strategy, the blue arrow represents the model errors increase after using the given strategy, and the green arrow represents there is no evident change after using the given strategy. From the three tables, the following conclusions can be drawn:

(1) The performance of most tree-ensemble models has improved after bias correction, except that the performance of XGBoost on the expressway dataset shows a slight decline.

(2) The forecasting performance of most tree-ensemble models have decreased after feature selection, regardless of the use of the feature importance measure (i.e., MDI or PI). This may be due to the feature selection strategy used in this study being too simplistic for the collected datasets, suggesting the need for more advanced strategies to enhance model performance.

(3) After employing both of the bias correction and feature selection strategies, the performance of the developed tree-ensemble models has generally improved, with only a slight decrease in the performance of a small number of models. This might be due to the negative effect of feature selection being offset by bias correction, thereby improving the overall model performance.

(4) In summary, for the developed tree-ensemble models, the bias correction strategy has a significant positive impact, while the effect of feature selection is less pronounced. It is necessary to explore more sophisticated feature selection strategies in traffic flow forecasting.

Model interpretability

In this section, comprehensive explanations for the developed tree-ensemble models under various scenarios were extracted using the interpretable machine learning methods. The consistency between daily traffic phenomena and the interpretability results, as well as the consistency among interpretations from different methods within the same category, is examined. As observed in Section 'Performance evaluation', the EF model shows a relatively competitive performance than the other tree-ensemble models. Therefore, we take the EF model as an example to illustrate the interpretability modeling procedure in the following subsections.

Local interpretability

Decision paths

The decision path for a given instance defines the decision path of the developed model from the root node to the leaf node. For each dataset, three typical instances collected at different time intervals were used to produce local interpretability of the EF model. The obtained decision paths for the different traffic flow instances are illustrated in Fig. 2. In the figure, the yellow dashed line indicates the position of the bias, i.e., the mean of the target variable in the training set, while the purple dashed line indicates the position of the final forecast. From the bias to the forecast, there is a decision path built by the model, where each path with an arrow represents the corresponding pull effect, either positive or negative (indicated by the red and blue horizontal lines), caused by a particular feature on the forecast. The greater the magnitude of the pull effect, the greater the contribution of the feature to the forecast. By inspecting the decision path plots, we can draw the following conclusions:

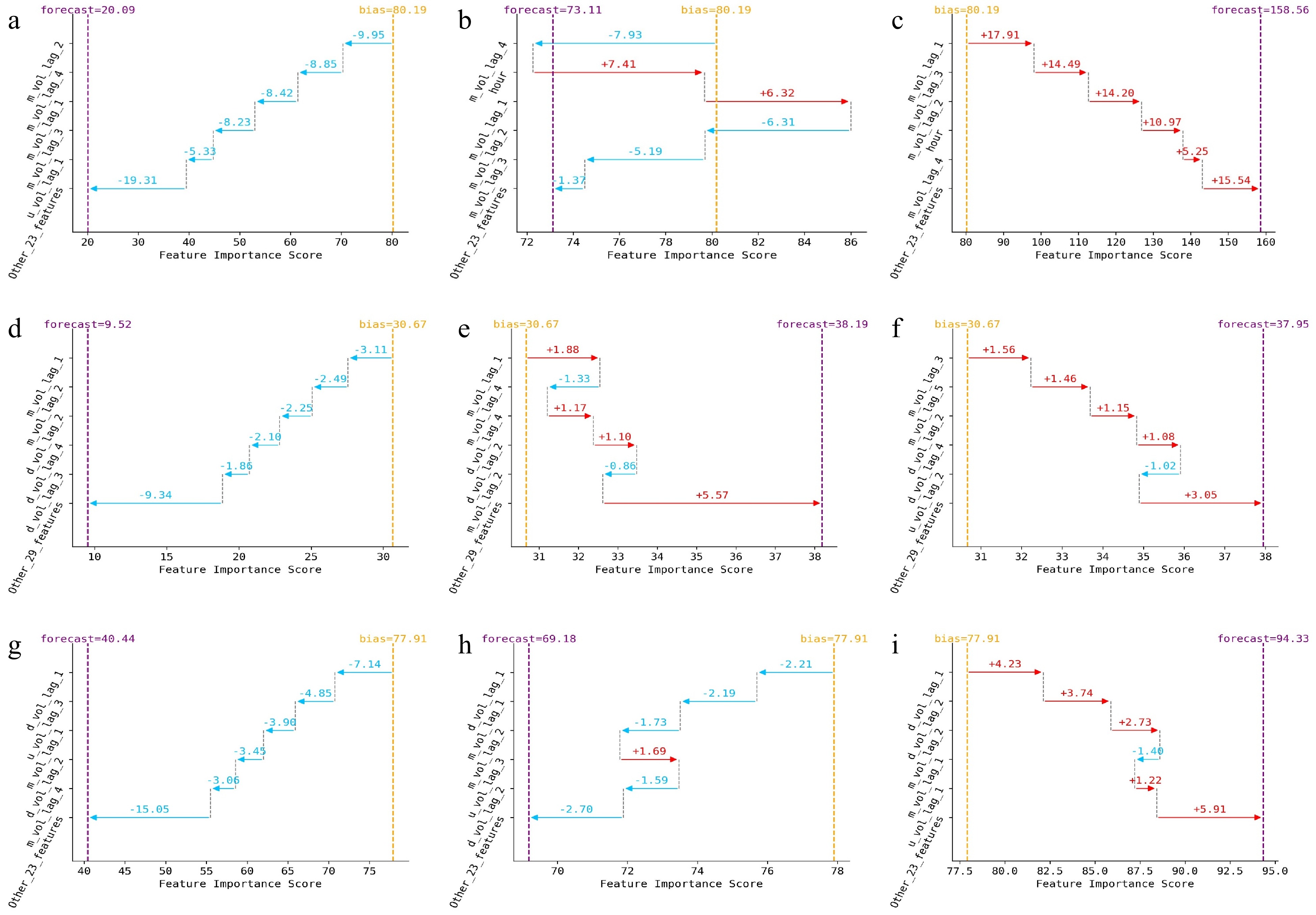
Figure 2. 

Local model explanations using decision path plots for different traffic flow instances. Arterial instance at (a) 5:30 am, (b) 6:30 am, (c) 7:30 am. Expressway instance at (d) 5:30 am, (e) 7:30 am, (f) 8:00 am. Freeway instance at (g) 5:30 am, (h) 6:30 am, (i) 7:30 am.

(1) Across the three datasets, there is a consistent shift in the contribution of features from negative to positive over time, which corresponds to the real-world phenomenon of lighter traffic in the early morning hours and heavier traffic during the morning peak. This indirectly confirms the reliability of the forecast. For example, at 5:30 am, there is no congestion on the roads. In this case, the model believes that all features should have a negative pull effect, causing the bias to slide towards a smaller forecast value. In contrast, at 7:30 am or 8:00 am, traffic on the road starts to get crowded. In this case, the model believes that most features should have a positive pull effect on the final forecast. During the above two time periods, the model believes that the contribution of features is different: some features (e.g., hour) would produce a positive pull effect and the other features (e.g., m_vol_lag_2) would produce a negative pull effect. Both categories of the features work together to achieve the final forecast.

(2) For different instances, the feature sets with top contribution are highly similar. It can be observed that the features with larger contributions are mainly related to the volume variable at the target location and downstream location. However, it can also be easily identified that the feature rankings in the feature sets are not exactly the same. The above observations confirm the need for both global and local interpretability approaches in explaining the developed models.

Individual Conditional Expectation (ICE)

ICE is a useful method to visually analyze the relationship between a given feature and the forecast of a model for individual instances. Figure 3 provides the ICE plots for different traffic flow datasets. In the figure, each blue line describes the partial dependence between a given feature and the forecast of an instance in the training datasets, and the black vertical lines show the value distribution of the feature. The following insights can be drawn from the figure:

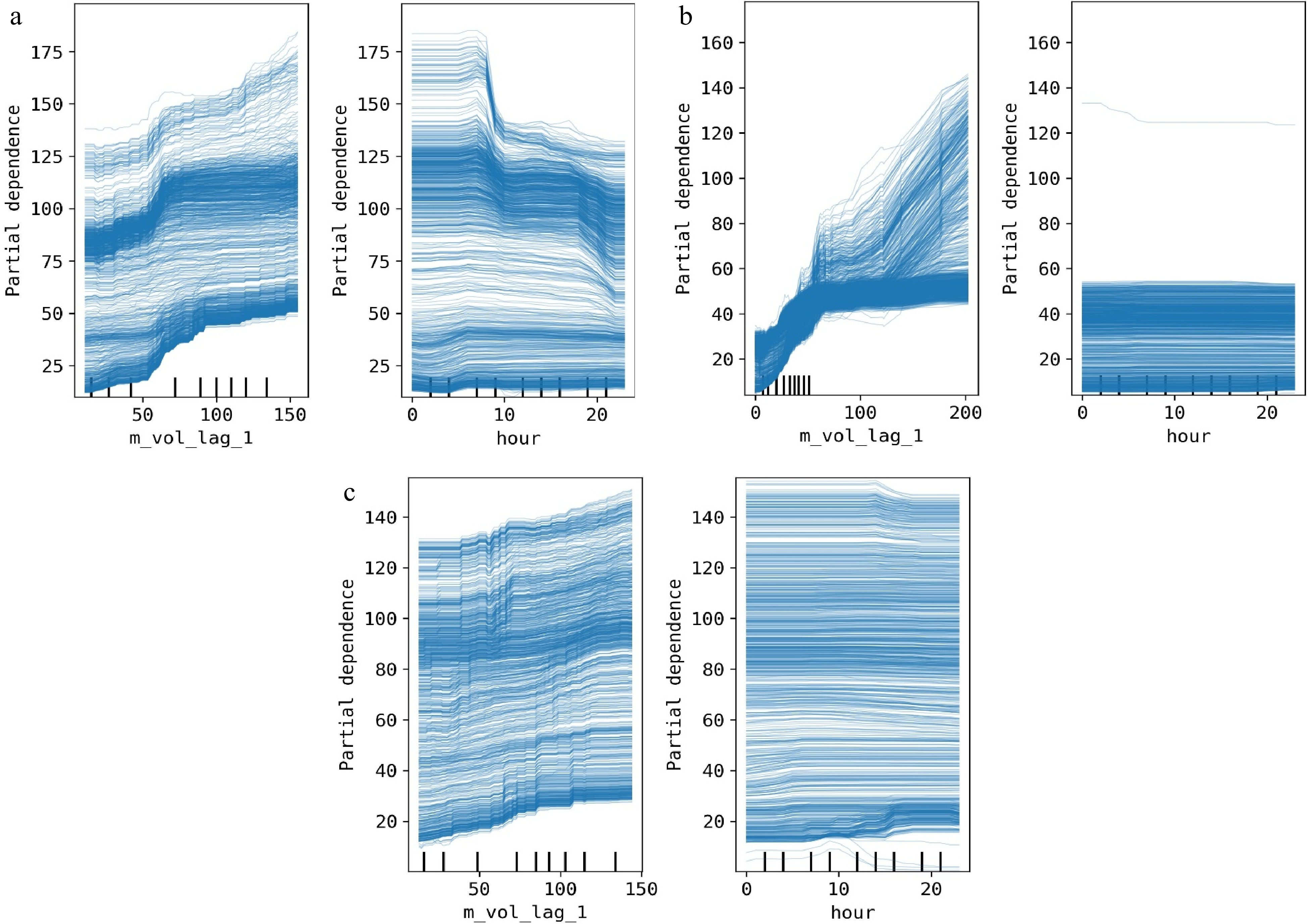
Figure 3. 

Local model explanations using ICE plots for different traffic flow datasets. (a) Arterial dataset, (b) expressway dataset, (c) freeway dataset.

(1) For the arterial dataset, the forecasted volume of the target location keeps increasing as the value of its first-order lagged feature (i.e., 'm_vol_lag_1') increases. For the seasonality feature, 'hour', the forecast of most instances exhibit a double-peak pattern of 'first increasing, then decreasing'. This phenomenon corresponds to the regular morning and evening peak patterns of traffic flow throughout the day.

(2) For the expressway dataset, the partial dependence of the forecast on the feature 'm_vol_lag_1' shows two distinct patterns. The first pattern is that the forecast values initially increase linearly with the feature values and then exhibit a slow growth trend. The other pattern is that the forecast values always increase linearly with the feature values. In contrast, the forecast values show almost no change with the increase of the 'hour' feature value, indicating that the contribution of the 'hour' feature is very small. This inference can be confirmed by the obtained global feature importance score in the following experiments.

(3) For the freeway dataset, the partial dependence of the forecast on the feature 'm_vol_lag_1' shows a similar pattern as the arterial dataset. For the 'hour' feature, the forecast values for some instances show a slight increase as the feature values increase during the morning and evening peaks, while the forecast values for the remaining instances do not change as the feature values increase.

SHapley Additive exPlanations (SHAP)

SHAP elucidates the developed models by measuring the impact of individual features based on the concept of Shapley values from cooperative game theory. The features with higher absolute Shapley values are deemed more influential. Figure 4 shows the beeswarm plots built on the estimated Shapley values for different traffic flow datasets. In the figure, the changing color value represents the value of the analyzed features. The variable on the horizontal axis is the calculated Shapley values. When the SHAP value is positive, it means the feature has a positive pull effect on the forecast; conversely, when it is negative, the feature possesses a negative pull effect. It is easy to identify the most informative features by inspecting the span range of the SHAP in the beeswarm plots. The following conclusions can be drawn from the figure:

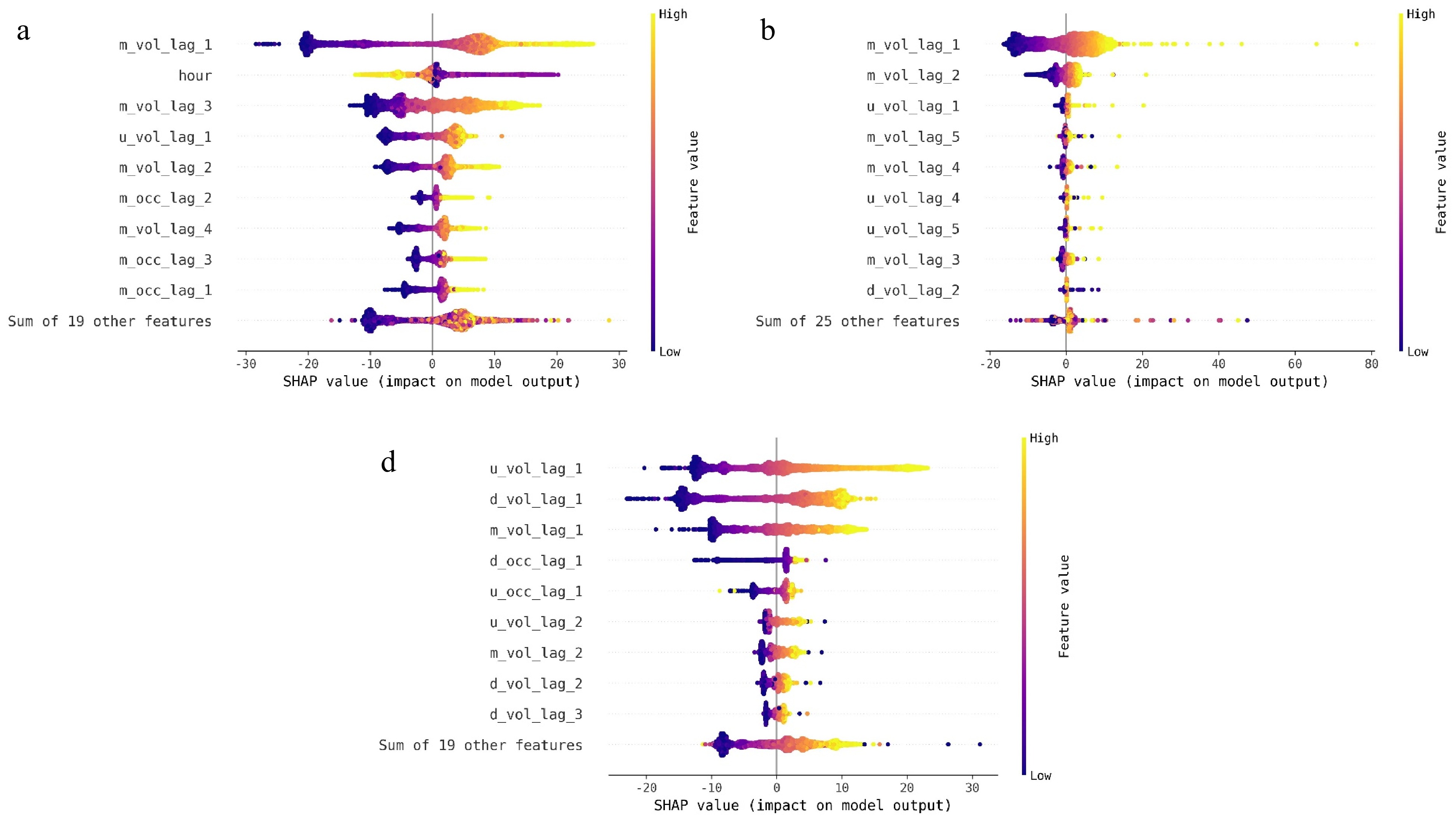
Figure 4. 

Local model explanations using beeswarm plots for different traffic flow datasets. (a) Arterial dataset, (b) expressway dataset, (c) freeway dataset.

(1) 'm_vol_lag_1' and 'u_vol_lag_1' are two features that have contributions to all of the three datasets. The larger the above feature value, the greater the positive pull effect on the forecast; the smaller the above feature value, the greater the negative pull effect on the forecast.

(2) For the arterial dataset, 'hour' plays a significant role in traffic volume forecasting. The 'hour' feature has a negative pull effect on the forecast when its value is very high (i.e., during late-night hours). Moreover, when the 'hour' feature value is in the middle range, it has a positive pull effect on the forecast. It needs to be indicated that the contribution of the 'hour' feature on the other two datasets is not significant.

(3) The number of informative features for the expressway dataset is smaller and more concentrated than that of the other two datasets since the associated beeswarm plot exhibits a more concentrated SHAP value distribution.

(4) Similar to the volume-related features, the occupancy-related features also have a positive pull effect on the model forecast when their values are large, and yields a negative pull effect when their values are small. The main difference is that the occupancy-related features do not contribute as much as the volume-related features.

Figure 5 depicts the waterfall plots built on the SHAP values associated with some typical instances from the three datasets. The waterfall plot is similar to the decision path plot. The main difference between the two plots is that the feature importance is quantified with different measures. In addition, the baseline value of the waterfall plot is the mean of the forecasted volume of the training dataset, while the baseline value of the decision path plot is the mean of the observed volume of the training dataset. In Fig. 5, the red color indicates a positive pull effect of the feature on the forecast, while the blue color indicates a negative pull effect. The following findings can be achieved from the figure:

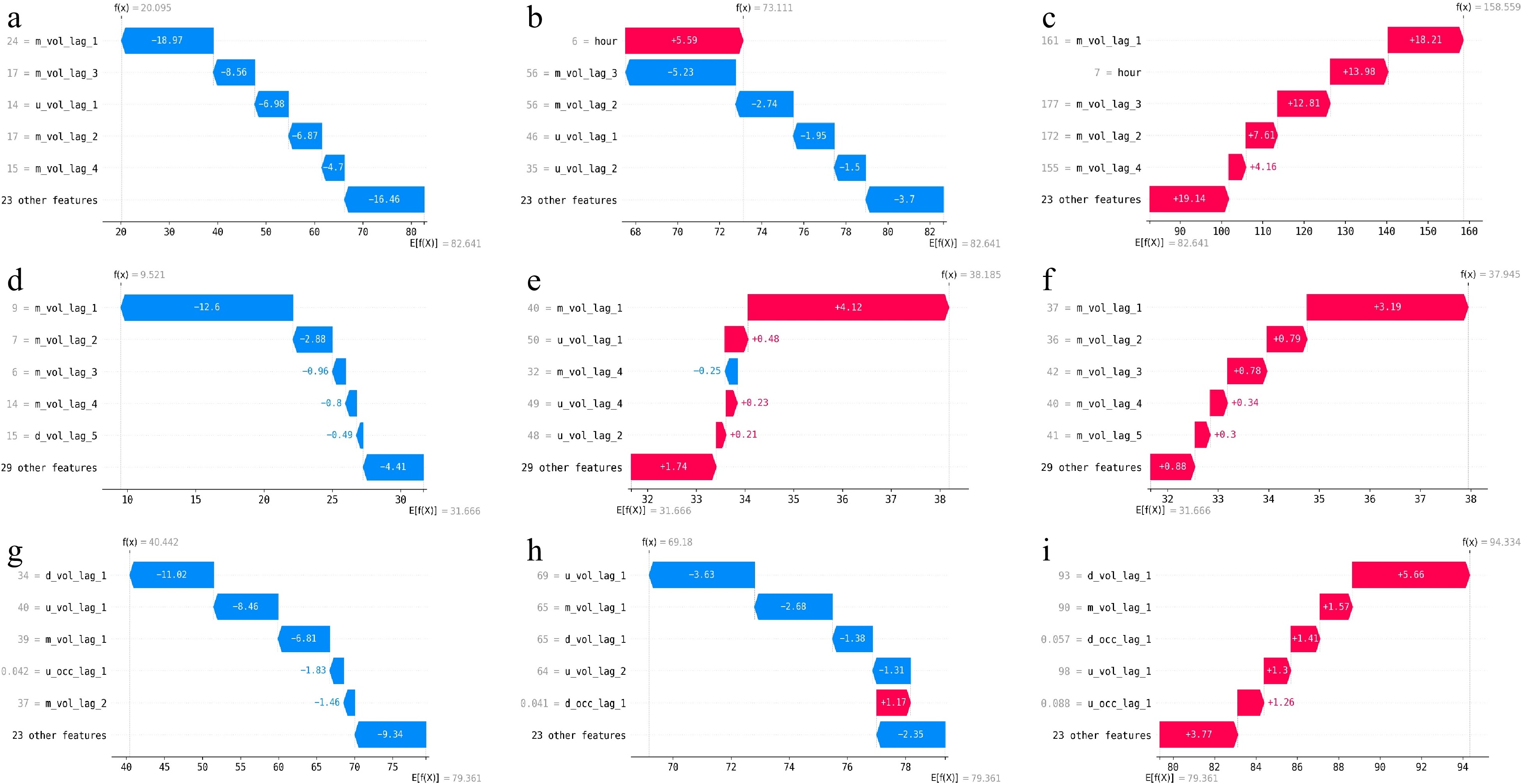
Figure 5. 

Local model explanations using waterfall plots for different traffic flow instances. (a) Arterial instance at (a) 5:30 am, (b) 6:30 am, (c) 7:30 am. Expressway instance at (d) 5:30 am, (e) 7:30 am, (f) 8:00 am. Freeway instance at (g) 5:30 am, (h) 6:30 am, (i) 7:30 am.

(1) All three datasets show a consistent trend of the pull effect of the features, shifting from negative to positive over time, which corresponds to real-world patterns of light traffic in the early morning hours and heavy traffic during the morning peak.

(2) The feature contributions vary across different datasets and time periods. Generally, the features related to volume are of the greatest importance. For the arterial and expressway datasets, 'm_vol_lag1' is treated as the most important feature in most cases, while for the freeway dataset, 'd_vol_lag_1', 'm_vol_lag1' and 'u_vol_lag1' are deemed more significant than the other features. It is worth mentioning that 'hour' is identified as the more informative feature for the arterial instances at 6:30 am and 7:30 am. This might be because during the above time periods, traffic on the road is getting congested and thereby plays a more evident guiding role in the forecasting task.

Global interpretability

Global feature mportance

The global feature importance method aims to rank the relevance or significance of each feature across the entire dataset and provides an overview of which features have the most impact on the forecast when considering all instances together. In the present study, three global feature importance methods were implemented, including MDI, PI, and SHAP. Figure 6 depicts the quantified global feature importance by the three methods for the three traffic flow datasets. The following observations can be made from the figure:

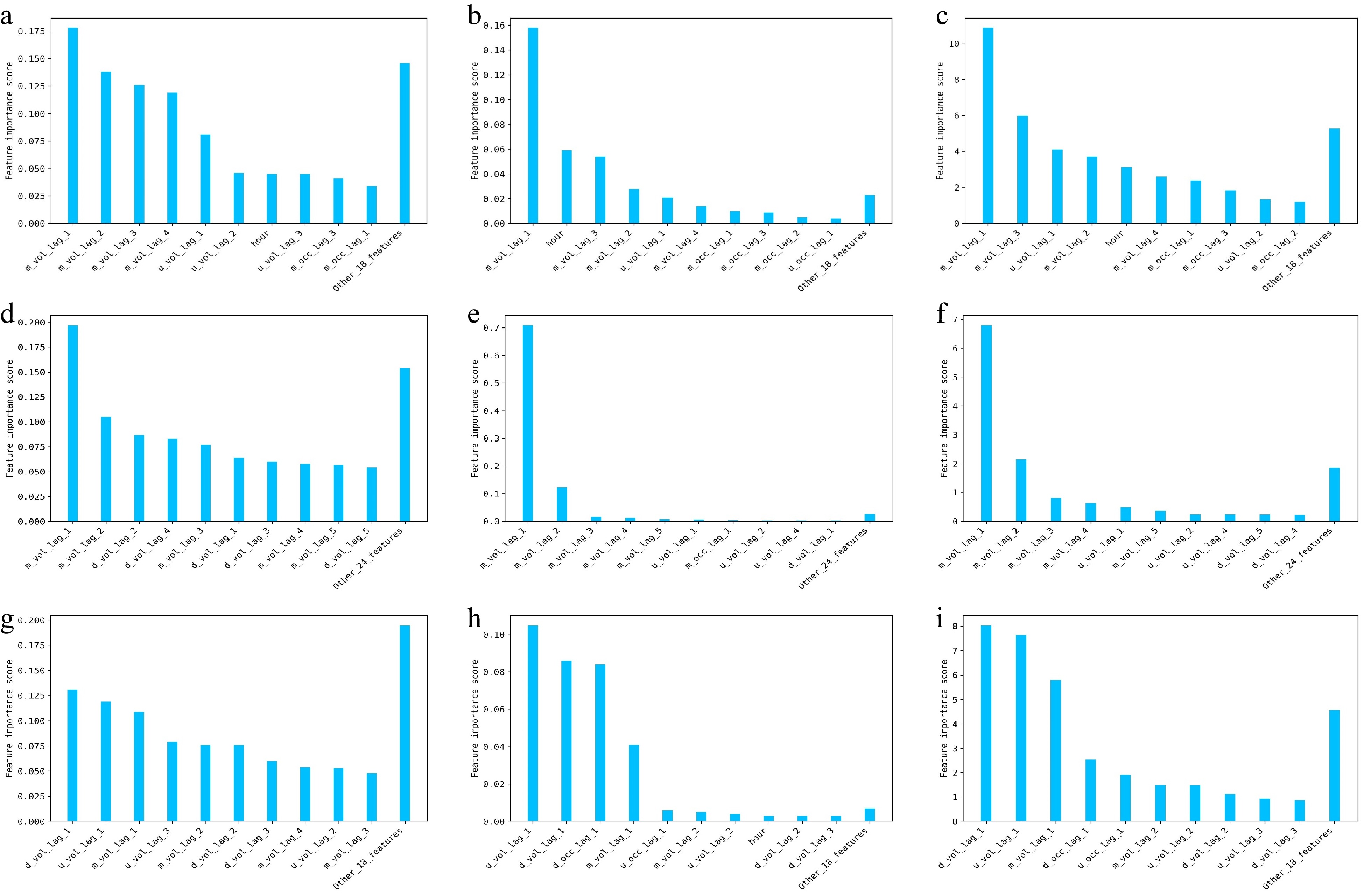
Figure 6. 

Global model explanations using global feature importance methods for different traffic flow datasets. (a) MDI / arterial dataset, (b) PI / arterial dataset, (c) SHAP / arterial dataset, (d) MDI / expressway dataset, (e) PI / expressway dataset, (f) SHAP / expressway dataset, (g) MDI / freeway dataset, (h) PI / freeway dataset, (i) SHAP / freeway dataset.

(1) For the arterial datasets, among the top five ranked features, all three methods consider 'm_vol_lag_1', 'm_vol_lag_2', 'm_vol_lag_3', and 'u_vol_lag_1' to be the most important features. However, both PI and SHAP methods believe that the 'hour' feature should be more important, while the MDI method suggests that 'm_vol_lag_4' should have a greater contribution.

(2) For the expressway datasets, the PI and SHAP methods assign higher contribution scores to 'm_vol_lag_1' and 'm_vol_lag_2', while the contribution scores assigned to other features are very small. In contrast, although the MDI method also considers the two features to be most informative, it assigns more even contribution scores to the other features.

(3) For the freeway dataset, all three methods assign more weight to 'm_vol_lag_1', 'd_vol_lag_1', and 'u_vol_lag_1'. However, both PI and SHAP methods suggest that 'd_occ_lag_1' should be given a higher contribution score, while the 'MDI' method still assigns relatively even scores to other features.

(4) From the above analysis, it can be seen that PI and SHAP show more similar behaviors in quantifying feature importance. As indicated by Molnar^[6], SHAP can provide fair and consistent feature importance quantification results, provided the Shapely values are properly estimated. In addition, PI is also able to yield reliable feature importance scores by directly measuring the impact of the given feature on model performance. The experimental results in our study confirm the above observations. Compared to PI and SHAP, MDI may provide biased scores towards features that allow more splits. It needs to be indicated that PI and SHAP are more computationally intensive than MDI. Therefore, in practice, PI and SHAP are the preferred choices for tree-ensemble models when computational resources allow.

Feature dependence

The feature dependence method evaluates the overall association between a feature and the resulting forecast or feature importance. 1D-PDP and SHAP dependence plots are two popular strategies for elucidating the feature dependence from a global perspective. Figure 7 provides the above two feature dependence plots for the three traffic flow datasets. The following conclusions can be drawn from the figure:

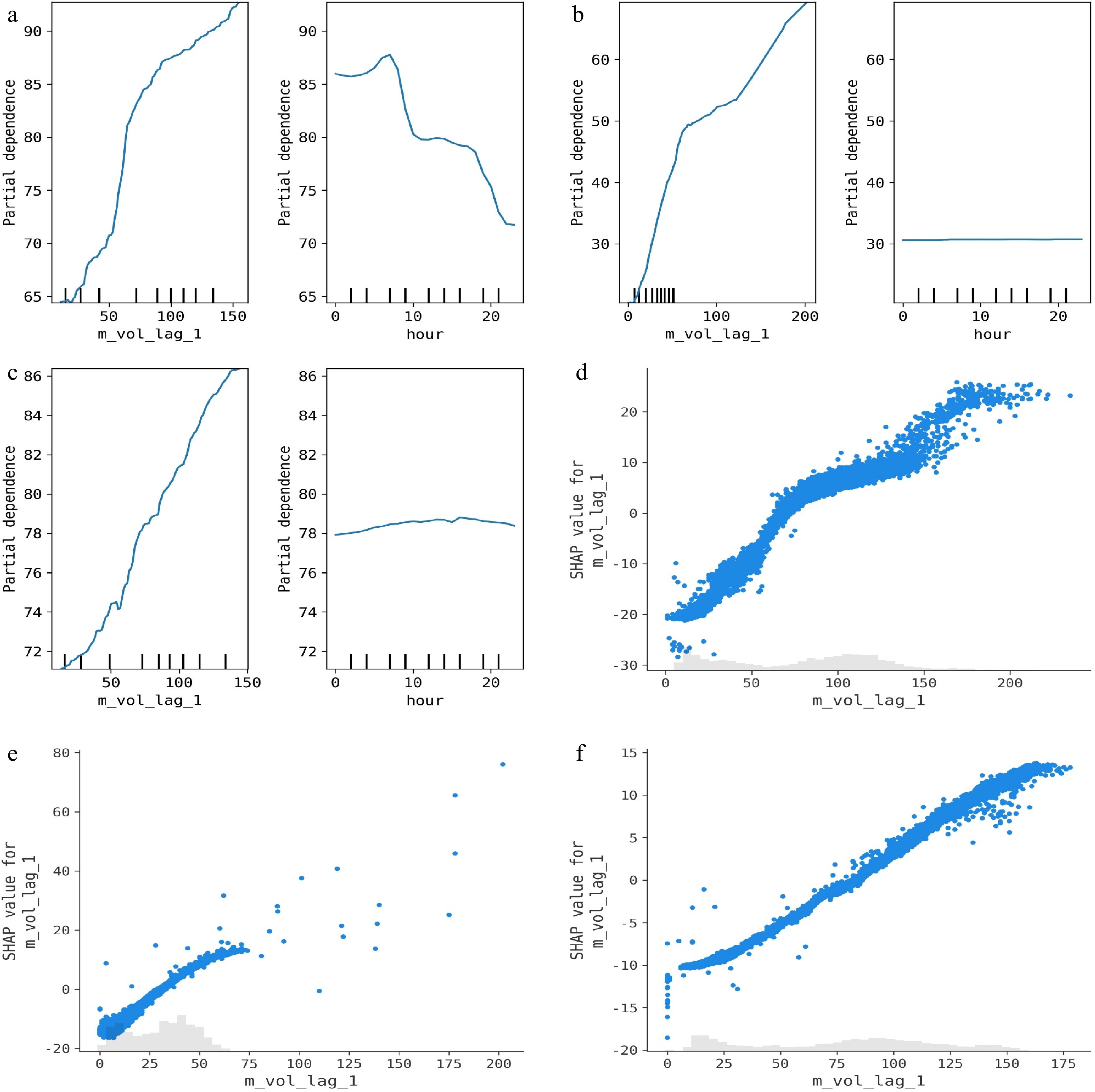
Figure 7. 

Global model explanations using feature dependence plots for different traffic flow datasets. (a) 1D-PDP / arterial dataset, (b) 1D-PDP / expressway dataset, (c) 1D-PDP / freeway dataset, (d) SHAP dependence plot / arterial dataset, (e) SHAP dependence plot / expressway dataset, (f) SHAP dependence plot / freeway dataset.

(1) Similar to ICE, 1D-PDP is also able to describe the trend of the forecasted values as a particular feature value changes. However, the dependence established by 1D-PDP is built on the whole dataset rather than individual instances. As can be seen from Fig. 7a−c, the forecasts almost increase linearly with the increase of 'm_vol_lag_1' and show a double-peak pattern for the arterial dataset while remaining stable for the other two datasets, regardless of changes in the values of 'hour'.

(2) SHAP plots built on the three datasets show very similar feature dependence as the 1D-PDPs. That is, as the value of 'm_vol_lag_1' increases, the SHAP values also increase hence the increase of the forecasted value. In addition, we can easily identify the value distribution of the given feature from the SHAP plot.

Feature interaction effect

The feature interaction effect method can be used to explain the interaction effect between different features on the forecasting output. 2D-PDP and the SHAP interaction plot are two popular methods for visually inspecting feature interaction effects. Figure 8 reveals the feature interaction relationships using 2D-PDP and the SHAP interaction plot for the three traffic flow datasets. Figure 8a, d & g visually describe the interaction effect of two sets of features (i.e., 'hour' vs 'm_vol_lag_1' and 'hour' vs 'u_vol_lag_1') on the forecasts by 2D-PDP, with lighter colors indicating greater forecasted value. Different colors are separated by a curve with specific forecasted values. The remaining part of Fig. 8 depicts the interaction effect of the two sets of features (i.e., 'm_vol_lag_1' vs 'u_vol_lag_1' and 'm_vol_lag_1' vs 'hour') on the SHAP values. The colors closer to blue indicate smaller feature values and the colors closer to red indicate larger feature values. The following findings can be achieved from the figure:

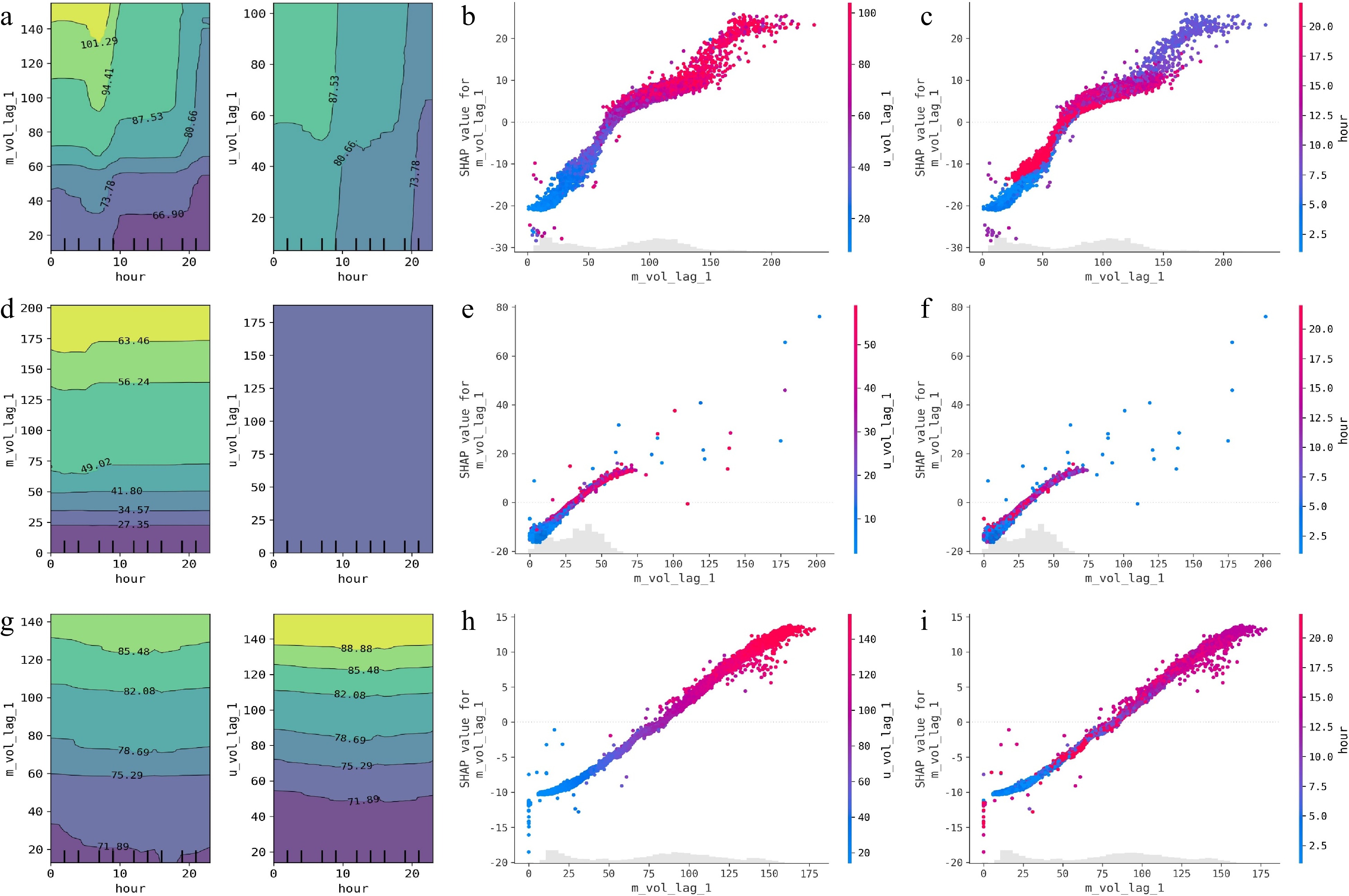
Figure 8. 

Global model explanations using feature interaction effect plots for different traffic flow datasets. (a) 2D-PDP / arterial dataset, (b) SHAP interaction plot-1 / arterial dataset, (c) SHAP interaction plot-2 / arterial dataset, (d) 2D-PDP / expressway dataset, (e) SHAP interaction plot-1 / expressway dataset, (f) SHAP interaction plot-2 / expressway dataset, (g) 2D-PDP / freeway dataset, (h) SHAP interaction plot-1 / freeway dataset, (i) SHAP interaction plot-2 / freeway dataset.

(1) For the 2D-PDP plots, the feature interactions between the given two features for the arterial datasets are more evident than that for the other two datasets, due to the fact that the contour lines associated with the former appear more curved and complex shapes. Furthermore, it can be observed from the contour line curves in Fig. 8a that the positive impact from the feature interactions on the forecasts intensifies and hence the forecasted values significantly increase during the peak hours.

(2) By analyzing the SHAP interaction plots, we can see that when the values of 'm_vol_lag1' and 'u_vol_lag1' are too small, the interaction of the two features has a negative impact on the forecasts, resulting in a negative pull effect. Similarly, when the value of the 'hour' feature lies in the peak periods, the feature produces the most significant positive pull effect. Moreover, it can be identified from Fig. 8c, f & i that on arterial roads and expressways, the traffic volume is higher during the morning peak compared to the evening peak, whereas on highways, the situation is reversed.

Traffic flow forecasting has been a research focus in the transportation field. In this study, an effective and interpretable traffic flow forecasting framework is presented that employs ensemble learning algorithms to build forecasting models and integrates interpretable machine learning methods to comprehensively explain these models. The framework consists of several key components incorporated into a flexible pipeline, including feature extraction, feature selection, bias correction, forecasting modeling, and interpretability modeling. The proposed framework was validated using traffic flow datasets collected from arterial, expressway, and freeway roads in China and the USA.

The contributions of this study are summarized as follows:

(1) A novel traffic flow forecasting framework was developed based on ensemble learning and interpretable machine learning. Within this framework, five traffic flow forecasting models were built using tree-ensemble algorithms (i.e., RF, EF, GBDT, XGBoost, and LightGBM) and compared with three kinds of typical models, including statistical time series, shallow learning, and deep learning. The experimental studies yielded the following findings:

● The proposed framework is both effective and flexible, capable of developing traffic flow forecasting models that offer competitive accuracy, high inference efficiency, and comprehensive interpretability.

● The bias correction component significantly enhances the performance of the tree-ensemble models and should be prioritized to improve predictive capabilities.

● A basic feature selection strategy is insufficient for enhancing model performance, highlighting the need for more advanced feature selection strategies.

(2) The interpretability of traffic flow forecasting models developed with tree-ensemble algorithms were thoroughly investigated. By employing six categories of interpretable machine learning methods, insights into the models' interpretability were provided from both local and global perspectives. These insights bridge the gap in decision-makers understanding of traffic flow forecasting models, thereby establishing a solid foundation for their reliable deployment and enhancing trust in intelligent transportation systems (ITSs).

Future research should focus on the following directions. First, the interpretability of tree-ensemble models were the primary focus in this study. In contrast, deep learning models often exhibit poorer interpretability and are typically considered 'black-box' models. Therefore, incorporating interpretable deep learning techniques into the proposed framework is necessary. Second, combining deep learning-based feature extraction mechanisms with the proposed framework could address issues related to feature unreliability during manual feature extraction, and considering more useful features, such as traffic regimes^[29,69], could also improve the development of traffic flow forecasting models. Third, conducting thorough experiments with a wider range of benchmark datasets, including those with extreme features such as adverse weather, accidents, and work zones, would provide a more comprehensive evaluation. Finally, while the present study centered on optimizing two of the hyperparameters for tree-ensemble models, future research should include more extensive hyperparameter tuning experiments to thoroughly assess the predictive power of these models.

The authors confirm contribution to the paper as follows: conceptualization: Ou J, Wang Y; methodology, software, writing – original draft: Ou J; funding acquisition: Ou J, Wang C; writing – review & editing: Li J, Nie Q; visualization: Li J; formal analysis, validation: Wang C; data curation: Wang Y; resource, supervision: Nie Q. All authors reviewed the results and approved the final version of the manuscript.

The datasets generated and/or analyzed during this study are available from the corresponding author upon reasonable request.