Search
Submit Manuscript
2.0CiteScore
Advanced Search
MAP  >  Food Materials Research
2024 Volume 4
Article Contents
Abstract
Introduction
Materials and methods
Plant materials
Protein extraction
Trypsin digestion
Affinity enrichment of ubiquitinated peptides
LC-MS/MS and data analysis
Bioinformatics methods
Results
Overview of the ubiquitomic analysis
Properties of ubiquitinated proteins and motifs
A temperature-regulated rice endosperm ubiquitome
Functions for differentially expressed ubiquitinated proteins
Discussion
Ubiquitination of heat shock proteins and transcription factors under high-temperature stress
Sucrose and starch metabolism are modified by ubiquitination under high-temperature stress
Ubiquitination affects sucrose hydrolysis
Ubiquitination of ADP-glucose pyrophosphorylase (AGPase)
Ubiquitination regulates amylose biosynthesis
Ubiquitination regulates amylopectin biosynthesis
Ubiquitination affects ribosomal systems under high-temperature stress
Author contributions
Data availability
Acknowledgments
Conflict of interest
Rights and permissions
References
About this article
Next Previous
ARTICLE   Open Access    

Modulation of rheological and textural properties in avocado pulp: impact of maltodextrin concentration and temperature

  • 1.

    Pos-Graduação Engenharia de Processos, Universidade Federal Campina Grande, Av. Aprigio Veloso 882, 58400-900 Campina Grande, Paraiba, Brazil

  • 2.

    Unidade Academica Engenharia de Alimentos, Universidade Federal Campina Grande, Av. Aprigio Veloso 882, 58400-900 Campina Grande, Paraiba, Brazil

More Information
  • The study of rheological and textural properties in fruit-based beverages is crucial for optimizing their sensory qualities and consumer appeal. This study investigated the effects of maltodextrin concentration and temperature on an avocado pulp rheological and textural properties. Using rheological models (Bingham, Ostwald-Waelle, and Cross), it was found that the beverage exhibited non-Newtonian, shear-thinning behavior. Maltodextrin was found to modulate these properties, reducing the initial flow barrier at lower concentrations and enhancing yield stress and viscosity at higher concentrations. Temperature also played a significant role, with lower temperatures yielding increased viscosity and yield stress. A thermodynamic analysis confirmed a direct relationship between maltodextrin concentration and activation energy, suggesting that maltodextrin forms a new structure within the avocado pulp that hinders molecular mobility. Textural parameters, including cohesiveness, consistency, firmness, and viscosity index, were all found to increase with maltodextrin concentration and decrease with temperature. These findings contribute to our understanding of the role of hydrocolloids and temperature in modulating fruit-based beverages' rheological and textural properties, offering significant implications for beverage formulation in the food industry.

  • Introduction

    Rice (Oryza sativa L.) is a world staple crop that feeds over half of the world's population[1,2]. In recent years, high-temperature events are becoming more frequent and intensive as a result of global warming, which can severely affect rice grain yield and quality[3,4]. During flowering and grain filling stages, high-temperature stress can result in a significant reduction in seed setting rate and influence amylose content, starch fine structure, functional properties and chalkiness degree of rice[5−7]. Transcriptome and proteome analysis in rice endosperm have also been used to demonstrate the differences in high-temperature environments at gene and protein expression levels[8−10]. In addition, as an important post-translational modification, protein phosphorylation has proven to be involved in the regulation of starch metabolism in response to high-temperature stress[11]. However, little is known about whether protein ubiquitination regulates seed development under high-temperature stress.

    Ubiquitination is another form of post-translational modification that plays key roles in diverse cellular processes[12]. Several reports have described the functions of ubiquitination in rice defense responses based on ubiquitome analysis. Liu et al.[13] investigated relationships between ubiquitination and salt-stress responses in rice seedlings using a gel-based shotgun proteomic analysis and revealed the potential important role of protein ubiquitination in salt tolerance in rice. Xie et al.[14] identified 861 peptides with ubiquitinated lysines in 464 proteins in rice leaf cells by combining highly sensitive immune affinity purification and high resolution liquid chromatography-tandem mass spectrometry (LC-MS/MS). These ubiquitinated proteins regulated a wide range of processes, including response to stress stimuli. A later study revealed the relationships between ubiquitination status and activation of rice defense responses, and generated an in-depth quantitative proteomic catalog of ubiquitination in rice seedlings after chitin and flg22 treatments, providing useful information for understanding how the ubiquitination system regulates the defense responses upon pathogen attack[15]. Although many studies have shown that ubiquitination plays improtant roles in the heat response of plant[16,17], there has been little systematic discussion on the ubiquitome of rice endosperm in the context of global climate change.

    In this study, we examine the high-temperature induced ubiquitination change in two rice varieties with different starch qualities, through a label-free quantitative ubiquitome analysis. This study provides a comprehensive view of the function of ubiquitination in high-temperature response of rice developing seed, which will shed new light on the improvement of rice grain quality under heat stress.

    Materials and methods

    Plant materials

    Two indica rice varieties with different starch quality, 9311 and Guangluai4 (GLA4), were used as materials. 9311 is a heat-sensitive variety, which displays low amylose content with good starch quality; while GLA4 is known to be the parental variety of HT54, an indica breeding line with heat tolerance, and thus GLA4 is possibly heat tolerant, which shows high amylose content with poor starch quality[18,19]. Rice growth conditions, sample treatment and collection were conducted as previously described[11].

    Protein extraction

    Husk, pericarp and embryo were detached from immature rice grains on ice[20]. Rice endosperm was then ground with liquid nitrogen, and the cell powder was sonicated 10 rounds of 10 s sonication and 15 s off-sonication on ice in lysis buffer (6 M Guanidine hydrochloride, pH 7.8−8.0, 0.1% Protease Inhibitor Cocktail) using a high intensity ultrasonic processor. Following lysis, the suspension was centrifuged at 14,000 g for 40 min at 4 °C to remove the debris. The supernatant was collected, and the protein concentration was estimated using BCA assay (Pierce BCA Protein assay kit, Thermo Fisher Scientific, Waltham, MA, USA) before further analysis.

    Trypsin digestion

    The protein mixture was reduced by DTT with the final concentration of 10 mM at 37 °C for 1 h, alkylated by iodoacetamide with a final concentration of 50 mM at room temperature in the dark for 0.5 h, and digested by trypsin (1:50) at 37 °C for 16 h. Then the sample was diluted by adding trifluoroacetic acid (TFA) to the final concentration of 0.1%. The enzymatic peptides were desalted on a Sep-Pak C18 cartridge (Waters, Milford, MA, USA), concentrated by lyophilization and reconstituted in precooled IAP buffer (50 mM MOPS-NaOH PH 7.2, 10 mM Na2HPO4, 50 mM NaCl) for further analysis.

    Affinity enrichment of ubiquitinated peptides

    The peptides solution was incubated with prewashed K-ε-GG antibody beads (PTMScan Ubiquitin Remnant Motif (K-ε-GG) Kit), and gently shaken at 4 °C for 1.5 h. The suspension was centrifuged at 2,000 g for 30 s, and the supernatant was removed. The Anti-K-ε-GG antibody beads were washed with IAP Buffer three times and with ddH2O three times. The peptides were eluted from the beads with 0.15% trifluoroacetic acid (TFA). Finally, the eluted fractions were combined and desalted with C18 Stage Tips.

    LC-MS/MS and data analysis

    LC-MS/MS analysis were performed using the methods of Pang et al.[11]. Raw mass spectrometric data were analyzed with MaxQuant software (version 1.3.0.5) and were compared with the indica rice protein sequence database (Oryza sativa subsp. indica-ASM465v1). Parameters were set according to Pang et al.[11]. All measurements were obtained from three separate biological replicates.

    Bioinformatics methods

    Quantification of the modified peptides was performed using the label-free quantification (LFQ) algorithm[11]. Differentially ubiquitinated sites (proteins) in response to high-temperature were identified by Student's t-test (p < 0.05, log2(fold-change) > 1) with at least two valid values in any condition or the ubiquitination sites that exhibited valid values in one condition (at least two of three replicates) and none in the other.

    Subcellular localization was performed using CELLO database (http://cello.life.nctu.edu.tw). Gene Ontology (GO) annotation proteome was derived from the AgriGO (http://bioinfo.cau.edu.cn/agriGO/). The differential metabolic profiles were visualized with MapMan software (version 3.6.0RC1). Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway annotation was performed by using KEGG Automatic Annotation Server (KAAS) software. A p-value of < 0.05 was used as the threshold of significant enrichment. SWISS-MODEL was used to generate the tertiary structure of GBSSI (SWISS-MODEL, http://swissmodel.expasy.org/). The figures were annotated with Adobe Illustrator (Adobe Systems, San Jose, CA, USA).

    Results

    Overview of the ubiquitomic analysis

    To elucidate how high-temperature stress influences rice developing endosperm at the ubiquitination level, a label-free analysis was performed to quantify ubiquitome from two indica rice varieties under normal (9311-C and GLA4-C) and high-temperature conditions (9311-H and GLA4-H). The distribution of mass error of all the identified peptides was near zero and most of them (71.5%) were between -1 and 1 ppm, suggesting that the mass accuracy of the MS data fits the requirement (Fig. 1a). Meanwhile, the length of most peptides distributed between 8 and 42, ensuring that sample preparation reached standard conditions (Fig. 1b).

    Figure 1.  Characteristics of the ubiquitinated proteome of rice endosperm and QC validation of MS data. (a) Mass error distribution of all identified ubiquitinated peptides. (b) Peptide length distribution. (c) Frequency distribution of ubiquitinated proteins according to the number of ubiquitination sites identified.
    DownLoad: Full-Size Img PowerPoint

    In all endosperm samples, a total of 437 ubiquitinated peptides were identified from 246 ubiquitinated proteins, covering 488 quantifiable ubiquitinated sites (Supplemental Table S1). Among the ubiquitinated proteins, 60.6% had only one ubiquitinated lysine site, and 18.7%, 8.1%, 5.3%, or 7.3% had two, three, four, or five and more ubiquitinated sites, respectively. In addition, four proteins (1.6%, BGIOSGA004052, BGIOSGA006533, BGIOSGA006780, BGIOSGA022241) were ubiquitinated at 10 or more lysine sites (Fig. 1c, Supplemental Table S1). The proteins BGIOSGA008317 had the most ubiquitination sites with the number of 16. It was noted that besides ubiquitin, two related ubiquitin-like proteins NEDD8 and ISG15 also contain C-terminal di-Gly motifs generated by trypsin cleavage, and the modifications of these three proteins cannot be distinguished by MS[21]. Here, the di-Gly-modified proteome therefore represents a composite of proteins modified by these three proteins. However, the sites from NEDD8 or ISG15 modifications were limited because they mediate only a few reactions in cells[21].

    Properties of ubiquitinated proteins and motifs

    To better understand the lysine ubiquitome changes in rice endosperm induced by high-temperature, we performed a Gene Ontology (GO) functional annotation analysis on all identified ubiquitinated proteins (Fig. 2a). In the biological process GO category, 'metabolic process' and 'cellular process' were mainly enriched, accounting for 75.1% and 74.1% of ubiquitinated proteins, respectively. In addition, 34.6% proteins were associated with 'response to stimulu', emphasizing the regulatory role of ubiquitination modification in response to high-temperature stress. From the cellular component perspective, ubiquitinated proteins were mainly associated with 'cellular anatomical entity' (99.4%), 'intracellular' (84.4%) and 'protein-containing complex' (29.9%). The molecular function category result suggested that these proteins were largely involved in 'binding' (62.7%), 'catalytic activity' (43.4%) and 'structural molecule activity' (16.5%). Furthermore, subcellular location annotation information indicated that 34.7%−39.4% proteins were located in the cytoplasm, and other were mostly located in the nucleus (23.5%−27.7%), plasma membrane (9.4%−11.4%), and chloroplast (9.6%−12.8%) (Fig. 2b). It is noteworthy that the ubiquitinated proteins located in the cytoplasm were decreased in high-temperature environments in both varieties.

    Figure 2.  Analysis of ubiquitinated proteins and motifs. (a) Gene ontology (GO) functional characterization of ubiquitinated proteins. (b) Subcellular localization of ubiquitinated proteins. From the inside out, the ring represents 9311-C, 9311-H, GLA4-C and GLA4-H, respectively. (c) Motif enrichment analysis of ubiquitinated proteins.
    DownLoad: Full-Size Img PowerPoint

    The following two significantly enriched motifs from all of the identified ubiquitinated sites were identified using MoDL analysis: [A/S]xKub and Kubxx[E/Q/R/V]x[E/G/L/P/Q/R/Y], which covered 84 and 100 sequences, respectively (Fig. 2c). Further analysis showed that the conserved alanine (A) and glutamic acid (E) were included in upstream and downstream of the ubiquitinated lysine sites in rice endosperm. A similar phenomenon also occurred in rice leaf[14], wheat leaf[22], and petunia[23], indicating that alanine (A) and glutamic acid (E) were likely to be the specific amino acids in conserved ubiquitination motifs in plants. Additionally, serine (S) was enriched at the position -2 (upstream) of the ubiquitinated lysine, while various amino acids such as arginine (R), glutamic acid (E), glutamine (Q), valine (V) were found at positions +3 and +5 (downstream).

    A temperature-regulated rice endosperm ubiquitome

    To detect possible changes in rice endosperm ubiquitome attributable to high-temperature stress, we then performed LFQ analysis on all quantifiable ubiquitination sites within our dataset. As shown in Fig. 3a, more ubiquitinated proteins, peptides and sites were detected in the treatment groups (9311-H and GLA4-H), suggesting that exposure to high-temperature stress may increase the ubiquitination events in rice endosperm. Only 282 common ubiquitinated sites in 158 proteins were quantifiable for all sample groups due to reversible ubiquitination induced by high-temperature (Fig. 3b). Principal component analysis (PCA) showed that three repeats of each sample clustered together, and four groups were clearly separated (Fig. 3c). Furthermore, the differentially expression profiles of ubiquitination sites (proteins) in 9311 and GLA4 under high-temperature stress were depicted to further understand the possible changes (Fig. 3d). Where LFQ values were missing, the data were filtered to identify those ubiquitination sites with a consistent presence/absence expression pattern. These analyses yielded 89 ubiquitination sites that were only present in 9311-H and six that were only present in 9311-C (Fig. 3d, Supplemental Table S2). Similarly, 51 differentially expressed ubiquitination sites were present in GLA4-H and 13 ubiquitination sites only occurred in GLA4-C (Fig. 3d & Supplemental Table S3). Beyond that, a total of 113 and 50 significantly changed ubiquitination sites (p < 0.05, log2(fold-change) >1) were screened out in 9311 and GLA4, respectively (Fig. 3d, Supplemental Tables S4 & S5). For subsequent comparative analysis, the ubiquitination expression profiles with consistent presence/absence and ubiquitination sites with significant differences in statistical testing were combined and named as 9311-Up, 9311-Down, GLA4-Up, and GLA4-Down, respectively (Fig. 3d). The number of significantly up-regulated ubiquitination sites was far greater than down-regulated ubiquitination sites in both 9311 and GLA4 varieties. These findings indicated that high temperature not only induced the occurrence of ubiquitination sites, but also significantly upregulated the intensity of ubiquitination. Beyond that, the magnitude of the up-regulation in 9311 was higher than that in GLA4 (Fig. 3b & d), indicating that the ubiquitination modification of heat-sensitive varieties was more active than heat-resistant varieties in response to high-temperature stress.

    Figure 3.  A temperature regulated rice endosperm ubiquitome. (a) The number of ubiquitinated proteins, peptides and sites detected in four group samples. (b) Venn diagram of ubiquitination sites (proteins) detected in four group samples. (c) PCA based on ubiquitination intensity across all four sample groups with three biological repetitions. (d) Differentially expression profiles of ubiquitination sites (proteins) in 9311 and GLA4 under high-temperature stress. The expression profiles of selected ubiquitination sites (p < 0.05, log2(fold-change) >1) were normalized using the Z-score and presented in a heatmap.
    DownLoad: Full-Size Img PowerPoint

    To further investigate the ubiquitination regulatory pattern under high temperature stress in two varieties, four groups with significantly regulated sites were analyzed. There were 37 ubiquitination sites showed the same regulatory trend in 9311 and GLA4, accounting for 17.8% and 32.5% of the total differentially expressed sites in 9311 and GLA4, respectively. Among them, 36 ubiquitination sites were upregulated and one site was downregulated (Fig. 4a). In addition, 159 upregulated ubiquitination sites and three downregulated sites were only present in 9311, while 53 upregulated sites and 15 downregulated sites were only present in GLA4. Moreover, nine ubiquitination sites showed opposite regulatory trends in 9311 and GLA4. A similar regulatory trend of ubiquitination proteins is shown in Fig. 4b. It is noted that some proteins had both upregulated and downregulated ubiquitination sites (Supplemental Tables S6 & S7), indicating that significant differences in ubiquitination were, to some extent, independent of protein abundance.

    Figure 4.  Comparison of differentially ubiquitinated sites and proteins in 9311 and GLA4 under high-temperature stress.
    DownLoad: Full-Size Img PowerPoint

    Functions for differentially expressed ubiquitinated proteins

    To understand the function of ubiquitination in response to the high-temperature stress of rice endosperm, we conducted GO enrichment-based clustering analysis of the differentially ubiquitinated proteins in 9311 and GLA4 at high temperature, respectively (Fig. 5). In the biological process category of 9311, proteins were relatively enriched in the carbohydrate metabolic process, polysaccharide metabolic process, starch biosynthetic process, cellular macromolecule localization, protein localization, intracellular transport, and phosphorylation (Fig. 5). For the molecular function analysis, we found that the proteins related to kinase activity, nucleotidyltransferase activity, phosphotransferase activity, and nutrient reservoir activity were enriched (Fig. 5). The two principal cellular components were intrinsic component of membrane and integral component of membrane (Fig. 5). There was no significantly enriched GO term in the GLA4 group due to the dataset containing relatively few proteins, and thus, further enrichment analysis was conducted on the proteins that were common to both varieties. The results showed that proteins were over-represented in carbon metabolism, including starch biosynthesis and metabolism, glucan biosynthesis and metabolism, and polysaccharide biosynthesis and metabolism (Fig. 5), indicating the importance of carbohydrate synthesis and metabolism in the ubiquitination regulatory network.

    Figure 5.  Enrichment analysis of differentially expressed ubiquitinated proteins based on Gene Ontology (GO) terms.
    DownLoad: Full-Size Img PowerPoint

    To identify pathways which were differentially ubiquitinated under high-temperature stress, the KEGG pathway-based clustering analysis was conducted. The results showed that the differentially ubiquitinated proteins in both 9311 and GLA4 were mostly abundant in the pathways of carbohydrate metabolism, starch and sucrose metabolism, folding, sorting and degradation, translation, ribosome, and protein processing in endoplasmic reticulum (Fig. 6a). In the 9311 group, the pathways of carbohydrate metabolism, starch and sucrose metabolism, glycosyltransferases, glycolysis, and energy metabolism were enriched in the differentially ubiquitinated proteins (Fig. 6b); while there was no significantly enriched KEGG pathway in the GLA4 group. We further found the proteins that were common to both varieties were only significantly enriched in the starch and sucrose metabolism pathways (p = 0.04). The ubiquitination proteins involved in the starch and sucrose metabolism mainly include: sucrose hydrolysis (SUS, FK, UGPase), and starch synthesis (AGPase, GBSSI, BEI, BEIIb, PUL, PHO1), which are discussed below.

    Figure 6.  KEGG classification and enrichment analysis of differentially ubiquitinated proteins. (a) Number of differentially ubiquitinated proteins based on KEGG classification in 9311 and GLA4. (b) KEGG enrichment analysis of differentially ubiquitinated proteins in 9311.
    DownLoad: Full-Size Img PowerPoint

    Discussion

    Although many reports have described specific examples of ubiquitination in rice defense responses[13,15,16], our knowledge on global changes in the developing endosperm ubiquitome under high-temperature stress is still lacking. In this study, a label-free quantitative proteomic analysis of ubiquitination was applied to examine the high-temperature induced ubiquitination change of two indica rice varieties (9311 and GLA4) with distinct starch quality. We identified many new lysine modification sites on proteins involved in various pathways, highlighting the complexity of the ubiquitination-mediated regulatory system in high-temperature stress responses in rice.

    Ubiquitination of heat shock proteins and transcription factors under high-temperature stress

    Heat shock proteins accumulate under various stresses and play important roles in plant defenses against abiotic stresses[24,25]. Research has shown that a number of heat shock proteins were prominent in the rice ubiquitome network, of which OsHSP71.1, and OsHSP82A showed increased ubiquitination levels under chitin and flg22 treatment[15]. Here, seven lysine residues on five heat shock proteins possessed ubiquitination modification in rice endosperm. Three sites (BGIOSGA011420-K78, BGIOSGA026764-K99, BGIOSGA029594-K106) showed significant up-regulation in 9311 under high-temperature stress, while in GLA4, the ubiquitination level of BGIOSGA011420-K78 was down-regulated. This differential ubiquitination of heat-tolerant and heat-sensitive varieties provided a basis for studying the regulation of post-translational modification of heat shock proteins under high-temperature stress, despite the regulatory role of those heat shock proteins being still unclear.

    Transcription factors (TFs) play an essential role in the regulation of gene expression. A total of three transcription factors were identified in the ubiquitination dataset, of which two were NAC family members. As one of the largest plant-specific TF families, NAC is involved in the responses to abiotic and biotic stresses[26]. The ubiquitination modification of K173 in BGIOSGA018048 was specifically expressed in the 9311-H group, which may affect the stress resistance level in high-temperature environments. In addition, two sites K148 and K149 of ERF TF family member BGIOSGA024035 was downregulated in GLA4 under high-temperature stress. This differential ubiquitination was likely to affect the expression of related genes regulated by this transcription factor.

    Sucrose and starch metabolism are modified by ubiquitination under high-temperature stress

    Ubiquitination affects sucrose hydrolysis

    The results of GO and KEGG enrichment analysis of differential ubiquitination proteins indicated that the sucrose and starch metabolic pathway was largely affected by ubiquitination regulation under high-temperature stress (Figs 5 & 6). The ubiquitination sites involved in sucrose and starch metabolism are listed in Table 1. To assess how high-temperature stress affects the crucial pathway, the significantly differential ubiquitination sites in 9311 and GLA4 were displayed in the heatmap of specific proteins (Fig. 7).

    Table 1.  Ubiquitination sites related to sucrose and starch metabolism in rice endosperm.
    Gene nameAnnotationProtein entryModification site(s)
    SUS1Sucrose synthase 1BGIOSGA010570K172, K177
    SUS2Sucrose synthase 2BGIOSGA021739K160, K165, K176, K804
    SUS3Sucrose synthase 3BGIOSGA026140K172, K177, K541, K544, K588
    FKFructokinaseBGIOSGA027875K143
    UGPaseUDP-glucose pyrophosphorylaseBGIOSGA031231K27, K150, K303, K306
    AGPS1ADP-glucose pyrophosphorylase small subunit 1BGIOSGA030039K94, K464, K484
    AGPS2ADP-glucose pyrophosphorylase small subunit 2BGIOSGA027135K106, K132, K385, K403, K406, K476, K496
    AGPL2ADP-glucose pyrophosphorylase large subunit 2BGIOSGA004052K41, K78, K134, K191, K227, K254, K316, K338, K394, K396, K463, K508, K513
    AGPL3ADP-glucose pyrophosphorylase large subunit 3BGIOSGA017490K509
    GBSSIGranule bound starch synthase IBGIOSGA022241K130, K173, K177, K181, K192, K258, K371, K381, K385, K399, K462, K517, K530, K549, K571, K575
    BEIStarch branching enzyme IBGIOSGA020506K103, K108, K122
    BEIIbStarch branching enzyme IIbBGIOSGA006344K134
    PULStarch debranching enzyme:PullulanaseBGIOSGA015875K230, K330, K431, K736, K884
    PHO1Plastidial phosphorylaseBGIOSGA009780K277, K445, K941
     | Show Table
    DownLoad: CSV
    Figure 7.  Sucrose and starch pathway at the ubiquitination levels in rice endosperm under high-temperature stress.
    DownLoad: Full-Size Img PowerPoint

    In cereal endosperm, sucrose is the substrate for the biosynthesis of starch. The formation of glucose 1-phosphate (G1P, used in starch synthesis, see below) from sucrose requires a series of enzymes[27]. Here, we found that sucrose synthase 1 (SUS1), SUS2, SUS3, fructokinase (FK), and UDP-glucose pyrophosphorylase (UGPase) were ubiquitinated among all sample groups (Table 1, Fig. 7). In the ubiquitome of seedling and leaf in japonica rice, ubiquitination sites have been found in SUS1, SUS2, UGPase, and FK, which were related to sucrose hydrolysis[14,15]. SUS catalyzed the process of cleaving sucrose into UDP-glucose (UDPG) and fructose. Two ubiquitination sites, K172 and K177, were identified in SUS1 in rice endosperm, which were also found in rice leaves[14]. A total of four ubiquitination sites were identified in SUS2, two of which were also reported in rice seedling and leaf, indicating the conservation of the lysine residues in different rice tissues. It was noted that all four ubiquitination sites in SUS2 were upregulated in high-temperature environments, although the regulated sites of 9311 and GLA4 were different. In 9311, the ubiquitination levels of K160, K174, and K804 were increased, while GLA4 was only upregulated in K176. The ubiquitination sites K541, K544, and K588 in SUS3 were screened from developing rice seeds for the first time. In addition, SUS3 had two completely overlapping sites K172 and K177 with SUS1, and it was difficult to determine which enzymes the two sites belonged to. The ubiquitination levels of SUS3-K541 and SUS3-K544 in 9311 significantly increased in high-temperature environments, while there was no significant difference in the ubiquitination level of SUS3 in GLA4. Overall, the ubiquitination sites of SUS in rice endosperm were located in the functional domain except for SUS2-K804, reflecting the importance of ubiquitination regulation in SUS.

    UGPase catalyses the conversion of glucose 1-phosphate and UTP into UDPG[28]. Research has shown that the mutation of UGPase gene lead to chalky endosperm[29]. As shown in Table 1, four ubiquitination sites K27, K150, K303, and K306 were identified in rice endosperm, which were completely inconsistent with the seven ubiquitination sites in rice seedlings and two in leaves[14,15], reflecting the tissue specificity. We speculated that the UGPase with different modification sites may play different regulatory roles in metabolic pathways in different tissues. Under high-temperature stress, the ubiquitination level of UGPase-K27 was 8.1-fold up-regulated. Liao et al.[10] demonstrated that the expression of UDPase was down-regulated in both heat-tolerant and heat-sensitive rice lines under high temperature conditions, which could reasonably explain the significant up-regulation of UGPase-K27 ubiquitination level. The ubiquitination site K143 of FK was also reported in seedling tissues[15].

    Ubiquitination of ADP-glucose pyrophosphorylase (AGPase)

    The AGPase reaction represents the first committed step of starch biosynthesis[27]. A total of 22 lysine ubiquitination sites were identified in four AGPase subunits (AGPL2, AGPL3, AGPS1, AGPS2). AGPL2 had 13 ubiquitination sites, of which six were located in NTP_transferase domain, including K254, K338, K191, K134, K227, and K316. High-temperature stress resulted in an increase in the ubiquitination level of K254 in both 9311 and GLA4, and significant upregulation of K508 and K513 in 9311, as well as K191, K227, and K316 in GLA4. In contrast, AGPL2-K394 were significantly downregulated in GLA4. AGPL3 contained one ubiquitination site K509, and the modification level of AGPL3-K509 was up-regulated in high-temperature environments in 9311. AGPS1 had one specific ubiquitination site K464 and another two sites K94 and K484 that completely overlapped with AGPS2-K106 and AGPS2-K496, respectively. The modification levels of K464 and K484 significantly increased in high-temperature environments in 9311, and K94 was significantly up-regulated in both varieties. There were seven ubiquitination sites in AGPS2 in rice endosperm, which were different with the sites found in rice leaves[14]. In addition to the two sites that overlapped with AGPS1, AGPS2 had another two ubiquitination sites (K406 and K132) that upregulated in high-temperature environments.

    Ubiquitination regulates amylose biosynthesis

    Amylose content is one of the key determinants that strongly influence rice grain quality[30]. The biosynthesis of amylose requires the catalytic effect of granule-bound starch synthase I (GBSSI)[30,31]. Here, a total of 16 ubiquitination sites were identified in GBSSI (Table 1, Fig. 8a). Among these ubiquitination sites, six lysine residues (K130, K173, K177, K181, K192, K258) were located in glycosyltransferase 5 (GT5) domain, and three sites (K399, K462, K517) were located in GT1 domain (Fig. 6), indicating the important role of ubiquitination regulation of GBSSI. Under high-temperature stress, the ubiquitination levels of six sites (K130, K177, K399, K381, K385, K549) increased in two indica rice varieties, while one sites (K258) showed downregulation in 9311 (Fig. 8a). Numerous studies had described that the amylose content was reduced under high-temperature stress in rice[5,7], which might be due to the degradation of GBSSI proteins caused by the increased significantly up-regulated ubiquitination sites. These ubiquitination sites identified in rice GBSSI with significant differences under high-temperature stress were expected to become a new breakthrough point for the improvement of starch quality.

    Figure 8.  Structure of GBSSI. (a) Domain structure of GBSSI and ubiquitination sites with significant differences in response to high-temperature stress. (b) 3D model of GBSSI and the relationship between ubiquitination sites K462 and ADP, SO4 (salt bridge or hydrogen bond).
    DownLoad: Full-Size Img PowerPoint

    To further determine the regulatory role of the ubiquitination sites in GBSSI, SWISS-MODEL was used to predict 3D structural model. As shown in Fig. 8b, GBSSI had three SO4 (sulfate ions) and one ADP ligand. These ligands interact with GBSSI through hydrogen bonds and salt bridges. Three sites, K447, R458, and K462, were associated with SO4 through salt bridges, while G100, N265, Q412, K462, and Q493 interact with the hydrogen bonds of ADP in GBSSI[32,33]. Based on this finding, it can be reasonably inferred that the K462 site with ubiquitination modification located in the GT1 domain played an important role in the interaction between GBSSI, SO4, and ADP. An in-depth investigation was necessary to gain a more comprehensive understanding of the regulatory function of ubiquitination modification at GBSSI-K462, although there was no significant difference in the ubiquitination level under high-temperature stress.

    Ubiquitination regulates amylopectin biosynthesis

    Amylopectin, the major component of starch, is synthesized by the coordinated action of multiple enzymes including soluble starch synthase (SSs), starch branching enzyme (BEs), starch debranching enzyme (DBEs), and phosphorylases (PHOs or Phos) with ADPG as a substrate. In this study, ubiquitination sites were detected in BEs, DBEs, and Phos.

    BEs, covering two isoforms, BEI and BEII, are responsible for catalyzing the formation of α-1,6-glucosidic linkages of amylopectin[34]. There were three ubiquitination sites (K103, K108, and K122) identified in BEI (Fig. 9a). K122 was the first amino acid in the carbohydrate-binding module 48 (CBM48) domain. Sequence alignment analyses of BEs from eight plants revealed K122 was conserved among all plants' BEI (Fig. 9a), suggesting a high probability of the functional effects of ubiquitination modification at this site. In high-temperature environments, ubiquitination levels of K108 and K122 were significantly up-regulated in 9311, while no significantly regulated ubiquitination sites of BEI were observed in GLA4. Only one ubiquitination site, K134, was found in BEIIb (Fig. 9a). The ubiquitination levels showed a slightly upward trend with no significant differences in high-temperature environments in both varieties. These changes could be one of the reasons for increased gelatinization temperature and relative crystallinity of rice starch in response to high-temperature[5].

    Figure 9.  Domain structure of (a) BEs, (b) PUL and (c) Pho1 as well as their ubiquitination sites with significant differences in response to heat stress. Residues in red indicate the ubiquitination site. Non-ubiquitinated residues are shown in dark grey.
    DownLoad: Full-Size Img PowerPoint

    DBEs consists of isoamylase (ISA) and pullulanase (PUL) with catalytic function for hydrolyzing α-1,6-glucosic linkages[35]. In the present study, we found that only PUL was ubiquitinated in rice endosperm (Fig. 9b). Among five ubiquitination sites (K230, K330, K432, K736, and K884) identified in PUL, K230 was located in the PULN2 domain, while K330 was in the CBM48 domain. Under high-temperature stress, K330 showed completely opposite regulatory trends in two cultivars. In addition, the ubiquitination level of K884, located in the DUF3372 domain, was significantly up-regulated in 9311. Previous study has reported that the expression of PUL was significantly up-regulated in 9311 under high-temperature stress, while GLA4 showed down-regulation in PUL abundance[11]. Consequently, there might be two possible functions of these ubiquitination sites. One possibility is that ubiquitination sites were unrelated to protein degradation; instead, they regulated the biosynthesis of amylopectin by affecting other functions of the protein. Secondly, ubiquitination sites were associated with protein degradation, and the levels of ubiquitination modification were based on protein abundance, resulting in a completely consistent regulation of ubiquitination modification and protein abundance under high-temperature stress.

    PHOs, including two types, Pho1/PHO1 and Pho2/PHO2, are responsible for the transfer of glucosyl units from Glc-1-P to the non-reducing end of a-1,4-linked glucan chains[36]. Pho1 is a temperature-dependent enzyme and considered crucial not only during the maturation of amylopectin but also in the initiation process of starch synthesis[37,38]. The three ubiquitination sites (K277, K445, K941) identified in Pho1 were located in two phosphorylase domains. We found that two sites, Pho1-K277 and Pho1-K445, were only ubiquitinated in high-temperature environments in 9311 and GLA4, respectively. Pang et al.[11] has demonstrated that the protein abundance of Pho1 decreased under high-temperature stress, especially in GLA4. Satoh et al.[38] reported that the functional activity of Pho1 was weakened under conditions of high temperature and its function might be complement by one or more other factors. Hence, these ubiquitination modifications that specifically occurred in high-temperature environments might be related to the degradation of Pho1 proteins.

    Ubiquitination affects ribosomal systems under high-temperature stress

    As a factory for protein synthesis in cells, the ribosome is an extremely crucial structure in the cell[39]. It has been proven that multiple ribosomal subunits were abundantly ubiquitinated in Arabidopsis and wheat[22]. In the present study, 57 ubiquitination sites involving 33 ribosome subunits were identified in 40S and 60S ribosome complexes in rice. Under high-temperature stress, the ubiquitination levels of some sites were significantly upregulated or downregulated, implying that ubiquitination of ribosomal proteins is likely to be an important regulatory mechanism in high-temperature response in rice endosperm. The results of GO and KEGG enrichment analysis indicated that the ribosome system was one of the most active systems for ubiquitination regulation under high-temperature stress. We speculated that the ubiquitin-proteasome system might be involved in the removal of subunits or entire ribosomes that were improperly folded in high-temperature environments. As shown in Fig. 10, the S10e, L18Ae, S27Ae, L9e, S3e, S28e, S20e, and S2e subunits were significantly up-regulated in 9311, while L13e subunits showed a completely opposite regulatory trend at the ubiquitination sites K81 and K88. In GLA4, the ubiquitination levels of S10e, S27Ae, L10Ae, L9e, S3e, S2e, and L4e showed a significant increase, while the ubiquitination level of L17e was significantly down-regulated under high-temperature stress. A total of seven ubiquitination sites involving S10e, S27Ae, L9e, S3e, and S2e subunits were jointly up-regulated in both two varieties. These sites might be related to the degradation of improperly folded ribosome subunits under high-temperature stress, while other ubiquitination sites with variety specificity might be associated with ribosomal function.

    Figure 10.  Ribosome system at the ubiquitination levels in rice endosperm under high-temperature stress. Grey shadings represent ubiquitinated proteins with no significant differences under heat stress. Red and blue shadings indicate up-regulated and down-regulated ubiquitinated proteins, respectively. Orange shading displays a combination of up- and down-regulated ubiquitinated sites in the same ubiquitinated protein.
    DownLoad: Full-Size Img PowerPoint

    In conclusion, this study provides the first comprehensive view of the ubiquitome in rice developing endosperm, and demonstrated that ubiquitination has diverse functions in the high-temperature response of rice endosperm by modulating various cellular processes, especially the sucrose and starch metabolism. Comparative analysis of the temperature-induced ubiquitination status revealed some similarities and more interesting differences between 9311 and GLA4. These differences might be the reason for the different qualities formation of the two indica rice varieties, which could provide potential genetic resources for the improvement of the heat resistance in rice. Considering the diversity of ubiquitination modification, it is worthwhile to further validate and explore the function and regulatory mechanism of the key targets and key pathways. The findings provide valuable insights into the role of ubiquitination in response to high-temperature stress and lay a foundation for further functional analysis of lysine ubiquitination in rice.

    Author contributions

    The authors confirm contribution to the paper as follows: study conception and design: Bao J, Pang Y; data collection: Pang Y; analysis and interpretation of results: Pang Y; draft manuscript preparation: Ying Y; Revised manuscript preparation: Ying Y, Pang Y, Bao J. All authors reviewed the results and approved the final version of the manuscript.

    Data availability

    The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

    Acknowledgments

    This work was financially supported by the AgroST Project (NK2022050102) and Zhejiang Provincial Natural Science Foundation (LZ21C130003).

  • The authors declare that they have no conflict of interest.

  • [1]

    Araújo RG, Rodriguez-Jasso RM, Ruiz HA, Pintado MME, Aguilar CN. 2018. Avocado by-products: Nutritional and functional properties. Trends in Food Science & Technology 80:51−60

    doi: 10.1016/j.jpgs.2018.07.027

    CrossRef   Google Scholar

    [2]

    Dantas D, Pasquali MA, Cavalcanti-Mata M, Duarte ME, Lisboa HM. 2018. Influence of spray drying conditions on the properties of avocado powder drink. Food Chemistry 266:284−91

    doi: 10.1016/j.foodchem.2018.06.016

    CrossRef   Google Scholar

    [3]

    Saavedra J, Córdova A, Navarro R, Díaz-Calderón P, Fuentealba C, et al. 2017. Industrial avocado waste: Functional compounds preservation by convective drying process. Journal of Food Engineering 198:81−90

    doi: 10.1016/j.jfoodeng.2016.11.018

    CrossRef   Google Scholar

    [4]

    Salazar-López NJ, Domínguez-Avila JA, Yahia EM, Belmonte-Herrera BH, Wall-Medrano A, et al. 2020. Avocado fruit and by-products as potential sources of bioactive compounds. Food Research International 138:109774

    doi: 10.1016/j.foodres.2020.109774

    CrossRef   Google Scholar

    [5]

    Kassim MS, Sarow SA. 2020. Flows of Viscous Fluids in Food Processing Industries: A review. IOP Conference Series: Materials Science and Engineering 870:012032

    doi: 10.1088/1757-899x/870/1/012032

    CrossRef   Google Scholar

    [6]

    Gupta MK, Torrico DD, Ong L, Gras SL, Dunshea FR, et al. 2022. Plant and dairy-based yogurts: a comparison of consumer sensory acceptability linked to textural analysis. Foods 11:463

    doi: 10.3390/foods11030463

    CrossRef   Google Scholar

    [7]

    Li MC, Wu Q, Moon RJ, Hubbe MA, Bortner MJ. 2021. Rheological aspects of cellulose nanomaterials: Governing factors and emerging applications. Advanced Materials 33:2006052

    doi: 10.1002/adma.202006052

    CrossRef   Google Scholar

    [8]

    Herazo MÁ, Ciro-Velásquez HJ, Márquez CJ. 2019. Rheological and thermal study of structured oils: Avocado (Persea americana) and sacha inchi (Plukenetia volubilis L.) systems. Journal of Food Science and Technology 56:321−29

    doi: 10.1007/s13197-018-3492-4

    CrossRef   Google Scholar

    [9]

    Freitas SP, Da Silva FC, Lago RCA, Qassim RY. 1996. Rheological behaviour of processed avocado pulp emulsions. International Journal of Food Science & Technology 31:319−25

    doi: 10.1046/j.1365-2621.1996.00340.x

    CrossRef   Google Scholar

    [10]

    Tabilo-Munizaga G, Moyano R, Simpson R, Barbosa-Canovas GV, Swanson BG. 2005. Flow and viscoelastic properties of pressurized avocado puree. Journal of Food Processing and Preservation 29:196−207

    doi: 10.1111/j.1745-4549.2005.00023.x

    CrossRef   Google Scholar

    [11]

    Osorio F, Roman A, Ortiz J. 2015. Effects of ripening on rheological properties of avocado pulp (Persea americana mill. Cv. Hass). Journal of Physics: Conference Series 602:012016

    doi: 10.1088/1742-6596/602/1/012016

    CrossRef   Google Scholar

    [12]

    Martínez-Padilla LP, Franke L, Juliano P. 2017. Characterisation of the viscoelastic properties of avocado puree for process design applications. Biosystems Engineering 161:62−69

    doi: 10.1016/j.biosystemseng.2017.06.016

    CrossRef   Google Scholar

    [13]

    de Oliveira Alencar DD, de Souza EL, da Cruz Almeida ET, da Silva AL, Oliveira HML, et al. 2022. Microencapsulation of Cymbopogon citratus D.C. stapf essential oil with spray drying: development, characterization, and antioxidant and antibacterial activities. Foods 11:1111

    doi: 10.3390/foods11081111

    CrossRef   Google Scholar

    [14]

    Mitschka P. 1982. Simple conversion of Brookfield R.V.T. readings into viscosity functions. Rheologica Acta 21:207−9

    doi: 10.1007/BF01736420

    CrossRef   Google Scholar

    [15]

    Martins GMV, de Sousa S, Duarte MEM, Cavalcanti-Mata MERM, Lisboa Oliveira HM. 2021. Modeling the combinatory effects of parboiling and cooking on red paddy rice (Oryza sativa L.) properties. LWT 147:111607

    doi: 10.1016/j.lwt.2021.111607

    CrossRef   Google Scholar

    [16]

    Tung MA. 1978. Rheology of protein dispersions. Journal of Texture Studies 9:3−31

    doi: 10.1111/j.1745-4603.1978.tb01292.x

    CrossRef   Google Scholar

    [17]

    Lima DB, Almeida RD, Pasquali M, Borges SP, Fook ML, Lisboa HM. 2018. Physical characterization and modeling of chitosan/peg blends for injectable scaffolds. Carbohydrate Polymers 189:238−49

    doi: 10.1016/j.carbpol.2018.02.045

    CrossRef   Google Scholar

    [18]

    Zheng H. 2019. Introduction: Measuring rheological properties of foods. In Rheology of semisolid foods, ed. Joyner H. Cham: Springer. pp. 3−30. https://doi.org/10.1007/978-3-030-27134-3_1
    [19]

    Balestra F, Cocci E, Marsilio G, Dalla Rosa M. 2011. Physico-chemical and rheological changes of fruit purees during storage. Procedia Food Science 1:576−82

    doi: 10.1016/j.profoo.2011.09.087

    CrossRef   Google Scholar

    [20]

    Bienvenue A, Jiménez-Flores R, Singh H. 2003. Rheological properties of concentrated skim milk: importance of soluble minerals in the changes in viscosity during storage. Journal of Dairy Science 86:3813−21

    doi: 10.3168/jds.S0022-0302(03)73988-5

    CrossRef   Google Scholar

    [21]

    Rao MA, Rizvi SS, Datta AK, Ahmed J. 2014. Engineering properties of foods. 4th Edition. Boca Raton: CRC Press. https://doi.org/10.1201/b16897
    [22]

    Pelegrine D, Silva F, Gasparetto C. 2002. Rheological behavior of pineapple and mango pulps. LWT 35:645−48

    doi: 10.1006/fstl.2002.0920

    CrossRef   Google Scholar

    [23]

    Udomrati S, Ikeda S, Gohtani S. 2013. Rheological properties and stability of oil-in-water emulsions containing tapioca maltodextrin in the aqueous phase. Journal of Food Engineering 116:170−75

    doi: 10.1016/j.jfoodeng.2012.10.032

    CrossRef   Google Scholar

    [24]

    Rao MA. 2014. Flow and functional models for rheological properties of fluid foods. In Rheology of Fluid, Semisolid, and Solid Foods. Boston, MA: Springer. pp. 27-61. https://doi.org/10.1007/978-1-4614-9230-6_2
    [25]

    Lira-Ortiz AL, Reséndiz-Vega F, Ríos-Leal E, Contreras-Esquivel JC, Chavarría-Hernández N, et al. 2014. Pectins from waste of prickly pear fruits (Opuntia albicarpa Scheinvar 'Reyna'): Chemical and rheological properties. Food Hydrocolloids 37:93−99

    doi: 10.1016/j.foodhyd.2013.10.018

    CrossRef   Google Scholar

    [26]

    Krokida MK, Maroulis ZB, Saravacos GD. 2001. Rheological properties of fluid fruit and vegetable puree products: compilation of literature data. International Journal of Food Properties 4:179−200

    doi: 10.1081/JFP-100105186

    CrossRef   Google Scholar

    [27]

    Nindo CI, Tang J, Powers JR, Takhar PS. 2007. Rheological properties of blueberry puree for processing applications. LWT - Food Science and Technology 40:292−99

    doi: 10.1016/j.lwt.2005.10.003

    CrossRef   Google Scholar

  • Cite this article

    Ribeiro S, Nascimento A, Lima J, Batista L, Almeida R, et al. 2024. Modulation of rheological and textural properties in avocado pulp: impact of maltodextrin concentration and temperature. Food Materials Research 4: e014 doi: 10.48130/fmr-0024-0005
    Ribeiro S, Nascimento A, Lima J, Batista L, Almeida R, et al. 2024. Modulation of rheological and textural properties in avocado pulp: impact of maltodextrin concentration and temperature. Food Materials Research 4: e014 doi: 10.48130/fmr-0024-0005
    shu

Figures(3)  /  Tables(4)

Download PDF

Article Metrics

Article views(2825) PDF downloads(460)

Other Articles By Authors

ARTICLE   Open Access    

Modulation of rheological and textural properties in avocado pulp: impact of maltodextrin concentration and temperature

  • 1.

    Pos-Graduação Engenharia de Processos, Universidade Federal Campina Grande, Av. Aprigio Veloso 882, 58400-900 Campina Grande, Paraiba, Brazil

  • 2.

    Unidade Academica Engenharia de Alimentos, Universidade Federal Campina Grande, Av. Aprigio Veloso 882, 58400-900 Campina Grande, Paraiba, Brazil

  • Received: 16 November 2023
  • Revised: 23 January 2024
  • Accepted: 15 March 2024
  • Published online: 07 May 2024
Food Materials Research  4,  Article number: e014  (2024)  |  Cite this article

Abstract: The study of rheological and textural properties in fruit-based beverages is crucial for optimizing their sensory qualities and consumer appeal. This study investigated the effects of maltodextrin concentration and temperature on an avocado pulp rheological and textural properties. Using rheological models (Bingham, Ostwald-Waelle, and Cross), it was found that the beverage exhibited non-Newtonian, shear-thinning behavior. Maltodextrin was found to modulate these properties, reducing the initial flow barrier at lower concentrations and enhancing yield stress and viscosity at higher concentrations. Temperature also played a significant role, with lower temperatures yielding increased viscosity and yield stress. A thermodynamic analysis confirmed a direct relationship between maltodextrin concentration and activation energy, suggesting that maltodextrin forms a new structure within the avocado pulp that hinders molecular mobility. Textural parameters, including cohesiveness, consistency, firmness, and viscosity index, were all found to increase with maltodextrin concentration and decrease with temperature. These findings contribute to our understanding of the role of hydrocolloids and temperature in modulating fruit-based beverages' rheological and textural properties, offering significant implications for beverage formulation in the food industry.

    HTML

    Introduction

    • The avocado (Persea americana Mill.), is a tropical and subtropical fruit, that originated from Central America and, more specifically, from Mexico, Guatemala, and West India[1]. Avocado is considered a complementary food with high nutritional value and bioactive components that could provide children with all benefits of fruits and vegetables[2]. Fruit suspensions consist of disintegrated vegetable cells and cell wall material dispersed in a fluid comprised of soluble components such as sugars, salts, and acids. However, avocado presents a particular chemical composition, rich in proteins, fibers, and lipids, which can provide rheological information different from other types of fruit pulps[3,4].

      Understanding the rheological properties of food products is essential for many industry segments. Rheological data is required for equipment design in extrusion, pumping, mixing, and agitation processes[5]. It is also important in food development and quality control as rheological data is linked to food texture, which is an important factor in food products' acceptability[6]. Finally, the fundamental understanding of food materials structures and interactions through the development of equations for rheological characterization is also an important feature to consider.

      Food products and especially fruit fluids typically present non-newtonian shear thinning behavior caused by a complex microstructure originating from a mixture of different components that can be either soluble or suspended[7]. Information about the rheological properties of avocado pulp and avocado pulp products is scarce since most articles focus on avocado oil[8]. The shear thinning behavior of avocado pulp and diluted avocado pulp has been described, revealing a pseudoplastic behavior with viscosity decreasing with avocado pulp concentration[9]. The effects of ultra-high pressure on the flow and viscoelasticity of avocado pulp revealed a shear thinning behavior but a lack of fit under the Herschel-Bulkley model[10]. The effects of ripening on the rheological properties of Avocado pulp revealed a Bingham plastic behavior[11]. More recently, the rheological properties were determined for avocado pulp after being minimally processed, high shear processed, or treated by malaxation, dilution, or sonication. Neither process altered the solid-like behavior of the avocado pulp. However, the storage moduli decreased with the mechanical treatments and water dilution, and both viscoelastic moduli increased with sonication treatment[12].

      Maltodextrin, a widely used polysaccharide in the food industry, especially in beverage systems, is essential for its functional properties like thickening, stabilizing, and bulking[2,13]. As a derivative of starch, it enhances mouthfeel and body in beverages without significantly increasing sweetness or altering flavor, making it ideal for health and energy drinks. Its use in avocado-based beverages is particularly intriguing for studying its interaction with avocado's fats and fibers, potentially altering viscosity, consistency, and sensory attributes. This research aims to understand how maltodextrin modulates the rheological and textural properties of avocado pulp, a key factor in developing innovative, functional, and appealing avocado-based beverages in response to growing consumer demand. However, there is a noticeable gap in understanding how avocado pulp interacts with additives like maltodextrin, particularly under varying temperature conditions, which are commonly encountered in industrial processing. Temperature variations can significantly impact the rheological properties of food products, influencing their processing, storage, and sensory attributes.

      Given the growing interest in avocado as a food product and its intensive processing in the industry, there is a clear need for more comprehensive rheological studies that take into account the effect of temperature. This research aims to bridge this gap by conducting detailed rheological and textural analyses under different temperature conditions. Specifically, the study seeks to elucidate the complex interactions between avocado pulp and maltodextrin across a range of temperatures, and how these interactions influence the flow properties of the pulp. Understanding the temperature-dependent behavior of these interactions is crucial for optimizing processing techniques and improving the quality of avocado-based food products, ensuring their stability and consistency under various storage and consumption conditions.

    Materials and methods

      Materials

    • Avocado (Persea Americana Mill.), were hand picked and bought at a local market. Commercial cow milk was also purchased at local supermarkets. Maltodextrin DE10 Corn Brazil was used as drying additive.

      Avocado pulp preparation

    • Avocado skin and kernel were hand removed and separated from the pulp. Then the five formulations were prepared as described in Table 1. Initially, the avocado was washed with abundant water, and then the bark and core were removed. The avocado pulp was placed in a knife homogenizer along with the desired amounts of water and maltodextrin. Each formulation was homogenized for 10 min. No other additives were used. Maltodextrin amounts were chosen to cover a wide range of concentrations.

      Table 1.  Tested avocado formulations and respective chemical composition.

      FormulationsUnitSM0SM5SM10SM20SM40
      Avocadog450450450450450
      Waterg10001000100010001000
      Maltodextring075.5151302604
      Chemical composition
      Waterg/100 g91.40 ± 0.1286.89 ± 0.2182.72 ± 0.2075.62 ± 0.1764.53 ± 0.19
      Proteing/100 g0.61 ± 0.0070.59 ± 0.0040.55 ± 0.0020.50 ± 0.0020.42 ± 0.001
      Lipidsg/100 g4.78 ± 0.0054.61 ± 0.0054.33 ± 0.0033.95 ± 0.0053.35 ± 0.003
      Ashg/100 g0.52 ± 0.0080.46 ± 0.00070.47 ± 0.0010.45 ± 0.0020.38 ± 0.005
      Carbohydratesg/100 g2.68 ± 0.0057.52 ± 0.0511.86 ± 0.0419.45 ± 0.0431.31 ± 0.03

      Rheological measurements

    • Viscosity and torque measurements were made on avocado mixtures using a Brookfield viscometer (RV+ model, Brookfield Engineering Laboratories Inc., MA, USA) at temperatures of 5, 25, and 35 °C with nine spindle speeds (1, 3, 5, 10, 20, 30, 50, 60, and 100 rpm). The temperature was maintained using a thermostatically controlled water bath. All data were taken after 30 s in each sample, with a rest in time between the measurements at different spindle speeds. Appropriate spindles (spindle no: 3 or 4) were used to get all readings within the scale. A 500 ml beaker was used for all measurements with the guard leg on and enough samples were added to just cover the immersion grooves on the spindle shafts. All experiments were replicated three times. Average shear stress and shear rates were calculated using the method of Mitschka[14].

      Texture analysis

    • Instrumental texture measurements were performed using a penetrometer (TA-TX plus, Stable Micro Systems, UK) equipped with a 50 N load cell. An A/BE-d35 probe was compressed twice against each bread sample of 25 mm to a defined depth (50%) at a rate of 1.7 mm/s. Measurements were performed in triplicate. As a result of these experiments, force–time curves were built and analyzed to determine the average of mechanical parameters (Firmness, Cohesiveness, Consistency and Viscosity index). The firmness parameter is related to the force required to attain a given deformation and is represented by the altitude of the first peak on the force-time curve. The cohesiveness parameter is related to the ability of the sample to resist deformation and maintain its structure. It is calculated as the ratio of the area under the force-time curve produced in the first compression to the area under the curve produced in the second compression. The consistency parameter is related to the resistance of the sample to deformation and is determined by analyzing the force-time curves. One common method is to calculate the area under the curve, which represents the work done on the sample during the test. A larger area under the curve typically indicates a higher consistency, as it suggests that more work is required to deform the sample. The viscosity index is a parameter related to the flow behavior of the sample under deformation. It is calculated as the ratio of the area under the force-time curve to the maximum force applied[15].

      Data modeling

      Rheological models

    • The term Bingham fluid typically represents a fluid with a yield stress and then a Newtonian behavior. Bingham fluid model is presented in Eqn (1):

      τ+τ0=Kγ (1)

      where, τ is the shear stress (Pa), τ0 is the yield stress (Pa), K the Bingham consistency index and γ is the shear rate (s−1). Ostwald-Waelle rheological model, or power law equation oss presented in Eqn (2).

      τ=Kγn (2)

      where, K is the consistency index (Pa·sn) and n is the flow behavior index.

      The apparent viscosity can be correlated with the shear rate through the adapted Cross model as presented in Eqn (3).

      η=η∞+η0−η∞(1+(αc⋅γ)m≈η0(1+(αc⋅γ)m (3)

      where, η the apparent or effective viscosity (Pa·s), η∞ is the infinite-shear-rate-viscosity, η0 is the zero-shear-rate-viscosity αC is the Cross time constant (s), m the Cross exponent. Since η0 values are much higher then η∞, the model was modified.

      Thermodynamic models for flow

    • Fluid flow is kinetically controlled so that an Arrhenius-type equation can be written:

      ηapp=Aexp(EaR⋅T) (4)

      where, ηapp is the apparent viscosity (Pa·s), A is a frequency factor associated with molecular collision rate (Pa·s), Ea is the activation energy (kJ/mol). R is the perfect gas constant (kJ/K mol) and T is the absolute temperature.

      Statistical analysis

    • All measurements were performed in triplicate. The results were evaluated by one-way analysis of variance (ANOVA) and average comparison by Tukey's test at 5% probability. All models presented significance relevance for a p < 0.05. Statistical work was performed using STATISCA 12.0, Statsoft, Tulsa, OK, USA.

    Results and discussion

      Rheological characterization of diluted avocado pulp

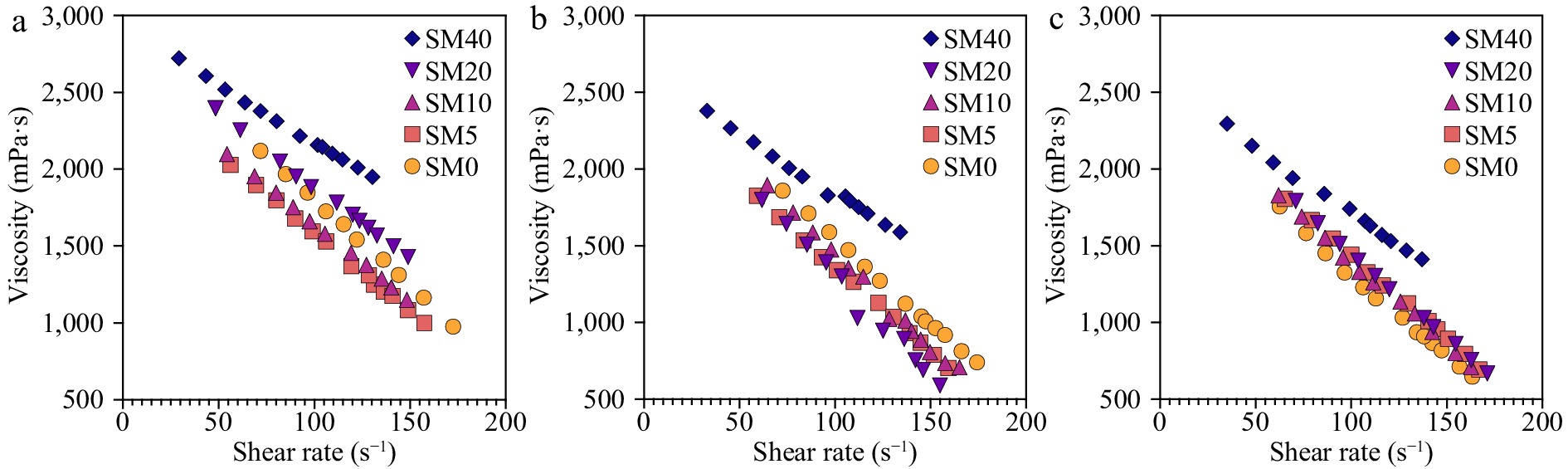
    • Rheological properties are essential for many industrial features and quality control but are also important to better understand the molecular interactions within the liquid material. Figure 1 presents the viscosity curves of all prepared samples at three different temperatures. All samples revealed thixotropic (shear thinning) properties throughout the entire range of shear rates used, revealing a non-Newtonian behavior since shear rate increases with shear stress, which can be generally explained by a mixture of dissolved and suspended compounds. This result agrees with other works using avocado, once Tabilo-Munizaga and co-workers also detected a shear thinning behavior for avocado puree[10]. However, from a rheological perspective, water, a main component of our formulation, is a Newtonian fluid. The rheology of these fluids is influenced by several parameters, being the most important the inter-particle forces. The shear thinning effect can be generally explained by asymmetric molecules aligned in shear planes, thereby reducing frictional resistance[16]. The presence of fat globules from avocados can significantly contribute to the shear thinning effect. Applying shear stress can progressively disrupt fat globules creating more agglomerates with smaller volumes and less interstitial volume. Therefore, reducing the fat volume fraction leads to less apparent viscosity explaining the shear-thinning behavior.

      Figure 1. 

      Viscosity curves for diluted avocado pulp at (a) 4 °C, (b) 25 °C, and (c) 37 °C.

      Temperature plays a significant role in influencing the viscosity of substances, including avocado pulp. The observed reduction in viscosity from 4 to 37 °C can be attributed to several factors, such as increased molecular motion and changes in the properties of fat globules and their interactions. As temperature rises, molecules move more rapidly, weakening intermolecular interactions like hydrogen bonding and van der Waals forces[17]. This leads to a decrease in viscosity as the substance flows more easily. In addition to molecular motion, the behavior of fat globules and other components like polysaccharides within avocado pulp can also be affected by temperature changes. As temperature increases, fat globules become more fluid and their interactions alter, contributing to the reduction in viscosity. Moreover, higher temperatures can cause changes in the conformation and solubility of polysaccharides and other components, impacting the overall viscosity of the pulp. Understanding these temperature-related changes is crucial for applications such as food processing and product development, as they can affect the final product's texture, stability, and quality.

      While maltodextrin is not typically considered an effective emulsifier, its amphiphilic nature and interaction with other components in a mixture can still influence the rheological properties of the system. In the case of the avocado-based samples, adding small amounts of maltodextrin led to a decrease in apparent viscosity, as shown in Fig. 2. This observation suggests that maltodextrin may interact with the fat globules in the avocado pulp, potentially causing some disruption in the globules or altering the balance between repulsive and attractive forces. However, it is essential to note that these effects may be limited and depend on the maltodextrin concentration. In the study, the apparent viscosity only started to increase after the maltodextrin concentration reached 20%. This increase in viscosity could be attributed to other factors, such as the thickening properties of maltodextrin or increased interactions between maltodextrin and other components in the system at higher concentrations. In summary, while maltodextrin is not a strong emulsifier, its presence, and interactions with other components, such as fat globules in avocado pulp, can impact the rheological properties of the mixture. The effects of maltodextrin on viscosity and emulsion stability may be concentration-dependent and should be considered when formulating food products containing both maltodextrin and avocado. This insight could be useful for optimizing products containing avocado and maltodextrin formulation, considering the desired rheological properties for specific applications.

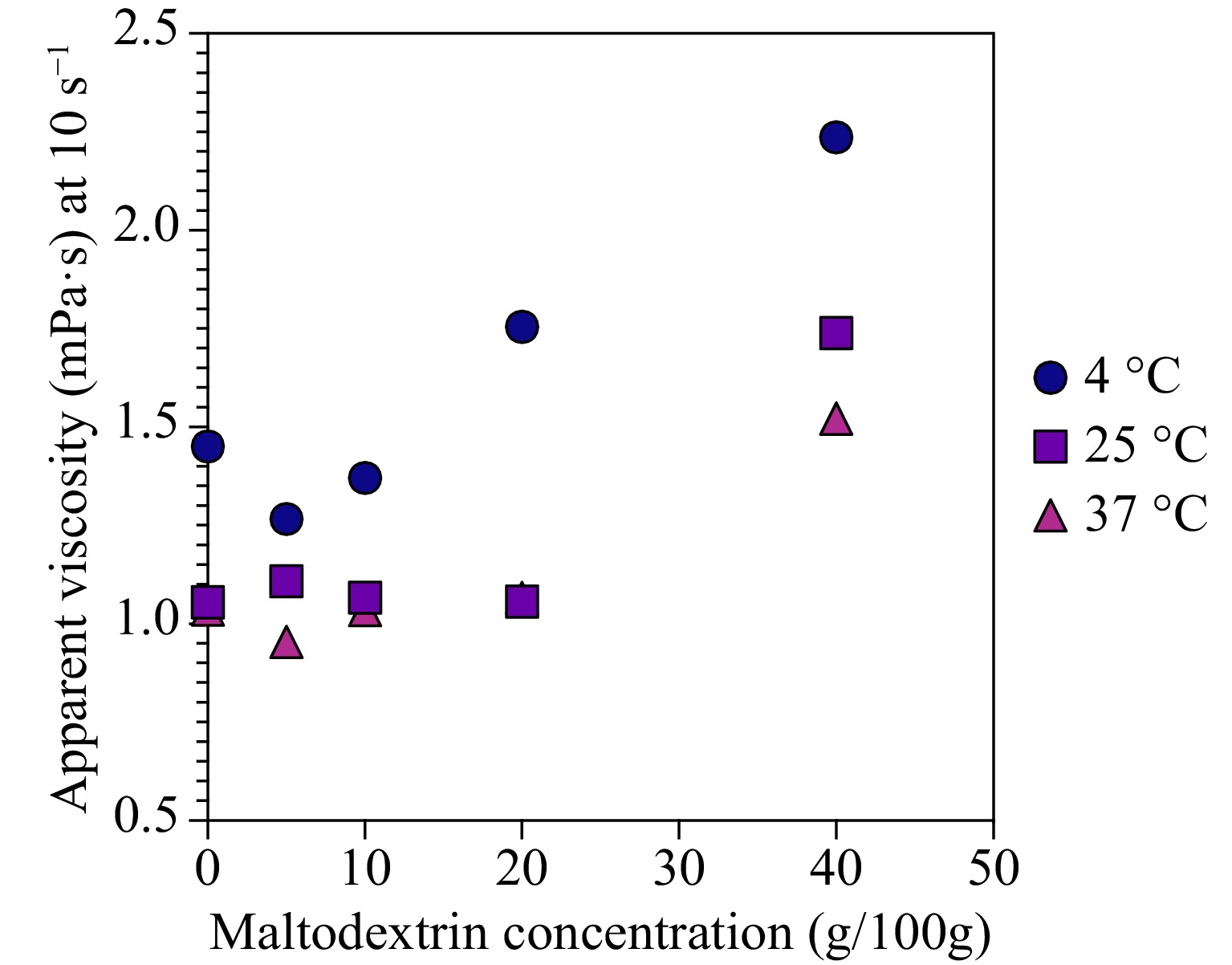
      Figure 2. 

      Effect of maltodextrin concentration on the apparent viscosity of diluted avocado pulp at 10 s−1 shear rate.

      Bingham flow modeling

    • Natural fluids require a critical level of stress to initiate flow. Below this critical value, fluids behave as solids absorbing stress without movement[18]. After reaching the critical level, the fluid yields to flow, hence the term yield stress. To determine the yield stress of the solutions and the impact of maltodextrin concentration, bingham model was fitted to the experimental data and the results summarized in Table 2. Yield stress values ranged from 24.84 to 12.71 and are influenced by temperature and maltodextrin concentration. Similar values for yield stress were observed for different fruit purees[19]. Moreover, yield stress values are higher for diluted avocado at 0% concentration of maltodextrin, and only after 20% of maltodextrin the yield stress surpass that initial value. Thus, small percentages of maltodextrin seem to reduce the initial flow barrier and act as a lubricant. At 25 and 37 °C, the initial flow barrier is similar for all maltodextrin concentrations, and only at the concentration of 40% is this value higher than the previous formulations. Yield stress reveals a three-dimensional structure that prevents flow at low shear rates. When higher shear rates are applied, the hydrodynamic forces disrupt secondary bonds such as ionic interactions and hydrogen bonds. Therefore, results can be explained by the formation of such a three-dimensional structure that firstly is interrupted by maltodextrin at low concentration but then, after a critical concentration, forms a new macromolecular structure. This is quickly identified at low temperatures because the density of secondary bonds is temperature dependent.

      Table 2.  Parameters determined for Bingham and Ostwald-Waelle flow model, and Cross Viscosity Model.

      SamplesTemperature (°C)τ0 (Pa·s)K (Pa·s)R2K (Pa·sn)nR2η0 (Pa·s)αC (s)γC (s−1)mR2
      SM0418.26 ± 0.150.057 ± 0.0020.97098.764 ± 0.10.22 ± 0.010.99851.1E+03 ± 1001145 ± 1158.7E-04 ± 0.00010.8 ± 0.080.9986
      2513.17 ± 0.120.060 ± 0.0030.99565.681 ± 0.080.27 ± 0.010.99951.4E+04 ± 14001486 ± 1496.7E-04 ± 0.000070.86 ± 0.0860.9965
      3713.00 ± 0.100.054 ± 0.0020.98335.819 ± 0.070.25 ± 0.010.99669.4E+03 ± 9404450 ± 4452.2E-04 ± 0.000020.75 ± 0.0750.9987
      SM5416.04 ± 0.180.095 ± 0.0040.98396.503 ± 0.090.29 ± 0.010.99985.2E+03 ± 5203661 ± 3662.7E-04 ± 0.000030.70 ± 0.070.9998
      2513.75 ± 0.130.044 ± 0.0020.98966.508 ± 0.080.23 ± 0.010.99652.4E+04 ± 24009180 ± 9181.1E-04 ± 0.000010.77 ± 0.0770.9996
      3711.96 ± 0.110.057 ± 0.0030.99105.135 ± 0.060.27 ± 0.010.99482.2E+04 ± 220015803 ± 15806.3E-05 ± 0.0000060.75 ± 0.0750.9970
      SM10416.88 ± 0.140.105 ± 0.0040.98866.738 ± 0.10.31 ± 0.010.99861.7E+03 ± 17022939 ± 22944.4E-05 ± 0.0000040.69 ± 0.0690.9983
      2513.13 ± 0.120.071 ± 0.0030.97845.452 ± 0.070.29 ± 0.010.99361.2E+03 ± 1206864 ± 6861.5E-04 ± 0.0000150.75 ± 0.0750.9993
      3712.94 ± 0.090.062 ± 0.0030.97175.578 ± 0.060.27 ± 0.010.99539.9E+03 ± 9904938 ± 4942.0E-04 ± 0.000020.75 ± 0.0750.9993
      SM20421.38 ± 0.200.179 ± 0.0050.99327.831 ± 0.110.35 ± 0.010.99751.4E+04 ± 140024449 ± 24454.1E-05 ± 0.0000040.66 ± 0.0660.9991
      2512.71 ± 0.110.063 ± 0.0020.99155.393 ± 0.070.31 ± 0.010.99201.2E+04 ± 120017054 ± 17055.9E-05 ± 0.0000060.72 ± 0.0720.9894
      3713.08 ± 0.100.047 ± 0.0020.99146.081 ± 0.080.27 ± 0.010.99172.8E+04 ± 280014109 ± 14117.1E-05 ± 0.0000070.77 ± 0.0770.9994
      SM40424.84 ± 0.250.472 ± 0.010.99467.429 ± 0.120.48 ± 0.020.99913.7E+03 ± 37041626 ± 41632.4E-05 ± 0.0000020.53 ± 0.0530.9989
      2519.41 ± 0.180.314 ± 0.0080.98746.026 ± 0.090.46 ± 0.020.99766.3E+03 ± 630131529 ± 131537.6E-06 ± 0.000000760.54 ± 0.0540.9961
      3717.28 ± 0.150.248 ± 0.0070.98725.509 ± 0.070.44 ± 0.020.99756.4E+03 ± 64042249 ± 42252.4E-05 ± 0.0000020.59 ± 0.0590.9632

      Additionally, when small percentages of maltodextrin are introduced, the fat globules may be affected by the altered balance of attractive and repulsive forces between the globules themselves and the maltodextrin molecules. The disruption of fat globules at low concentrations of maltodextrin could explain the reduced initial flow barrier and the lubricating effect observed. As the concentration of maltodextrin increases, it may lead to a new macromolecular structure that interacts with the fat globules and other components, causing an increase in yield stress.

      Furthermore, temperature changes can impact the behavior of fat globules, affecting their fluidity and interactions within the system. Fat globules are more likely to maintain their structure at lower temperatures, leading to a higher density of secondary bonds and more pronounced yield stress. As the temperature increases, fat globules become more fluid, reducing the strength of these secondary bonds and lowering the yield stress. Bienvenue et al. identified increases in yield stress when concentrated milk was stored for more extended periods due to the formation of more secondary bonds between milk molecules[20]. Consistency index values vary between 0.054 to 0.472 Pa·s, generally increasing with maltodextrin concentration and decreasing with temperature.

      Ostwald-Waelle flow

    • To better understand the deviation from the Newtonian fluids, the experimental data was fitted with the Ostwald Waelle (Power law equation). Results for both parameters are summarized in Table 3. The flow curves generated by the data fitting are presented in Fig. 3. From Table 2, considering that the R2 values are all above 99%, it is concluded that the power law model fits well the experimental data. Consistency indexes are similar to the constant dynamic viscosity of Newtonian fluids and the obtained values ranged from 5.135 to 8.764 Pa·sn. Accordingly, to Rao and co-workers, these values can be considered high, and typical of purees with high solid concentrations[21]. The effect of maltodextrin concentration is not clear since values can be considered constant throughout the entire series of concentrations. Even comparing the SM0, which has no maltodextrin, with the others, no clear differences are identified. However, with temperature, it is possible to identify higher values at 4 °C, but similar values at 25 and 37 °C. Higher consistency indexes do not necessarily guarantee a fluid with higher viscosity because this property also depends on the flow behavior and shear rate for shear-thinning fluids. For a solution to be considered a Newtonian fluid, the flow index value should be 1 as viscous stress and strain rate would be related by a constant dynamic viscosity (τ = μ·γ). However, the power law equation fitted to the experimental data gave values for flow index ranging from 0.222 to 0.436, meaning that all studied solutions were non-newtonian. Since the flow index is lower than 1, all samples presented shear-thinning properties where increasing shear rate results in lower apparent viscosity or higher stress is required to flow (Fig. 2). The more the flow index is close to 1 the less shear thinning the sample is. Similar values of consistency index and flow behavior where obtained for mango and pineapple pulps[22]. Thus, analyzing Table 2, it is clear that maltodextrin concentration have small impact on the flow index since values are almost constant until 20%. Above 20% the flow index suffers a sharp increase for all temperatures, meaning that fluid is less shear thinning effect. This can be explained by an overlap between the hydrodynamic domains of the maltodextrin coils. Once a given shear rate is reached, such maltodextrin coils start to disentangle and become aligned on the shear rate plane and interact via hydrogen bonds in a similar fashion to starch retrogradation. However, because the concentration has exceeded the critical concentrations, the disentanglements are less pronounced, and thus the shear thinning is also less pronounced. Similar behavior was detected on oil/water emulsions containing tapioca maltodextrin, where increasing concentrations of maltodextrin resulted in less shear thinning fluids[23]. It is also known that maltodextrin solutions are Newtonian fluids.

      Table 3.  Arrhenius-type equation parameters for apparent viscosity of diluted avocado pulp samples.

      Activation energy (kJ/mol)A (Pa·s)R2
      SM05.96 ± 0.61.8E-2 ± 0.00160.9635
      SM57.35 ± 0.331.1E-2 ± 0.00230.9734
      SM108.32 ± 0.657.52E-3 ± 0.000490.9798
      SM2012.93 ± 0.342.25E-4 ± 0.00003450.9666
      SM4010.36 ± 0.238.23E-3 ± 0.0004310.9943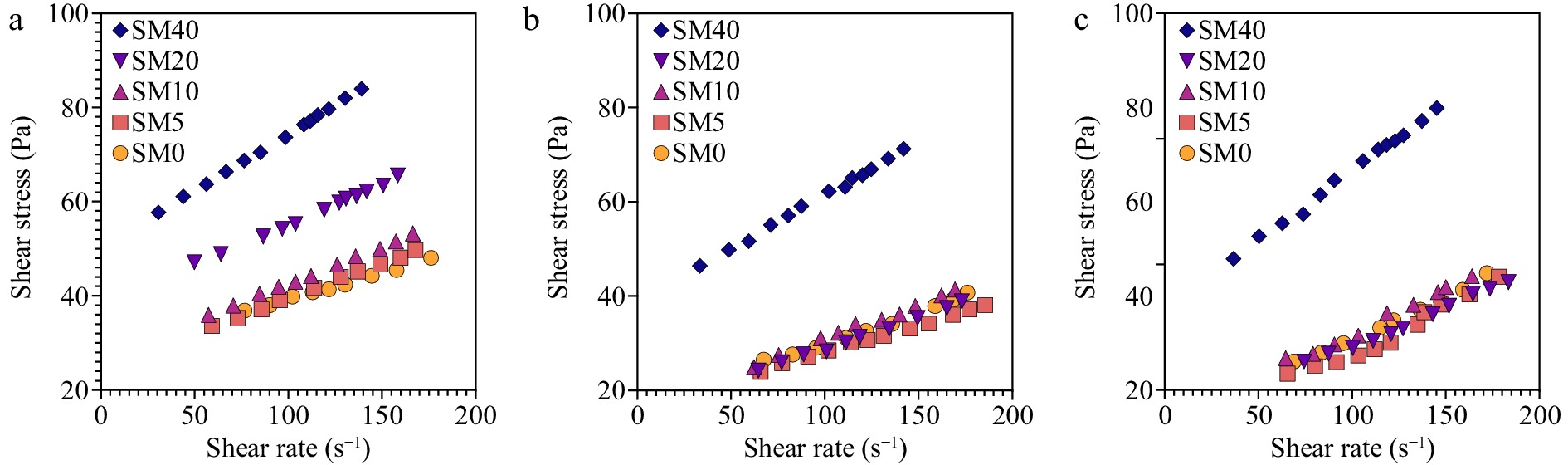

      Figure 3. 

      –Flow curves for avocado formulations at (a) 4 °C, (b) 25 °C, and (c) 37 °C modelled using Ostwald-Waelle models.

      Cross model

    • Cross model has been used to evaluate the rheological properties of polysaccharides where coil entanglements are present[24]. Shear thinning dispersions often exhibit three stages of viscous response when sheared at a wide range of shear rates. At low shear rates, fluids tend to present Newtonian properties with a zero-shear-constant η0 viscosity that is followed by a second stage, that is the typical shear thinning range where the viscosity drops as a function of the shear rate. At the third stage, fluids reach a constant infinite-shear-rate viscosity.

      Results for all parameters are presented in Table 2. Zero-shear-viscosity ranged between 103 to 104 with no clear trend for any of the parameters used. The reciprocal of cross time constant, (αC = 1/γC ) gives the order of magnitude of the critical shear rate that marks the end of the Newtonian plateau region and the beginning of the shear thinning region. Values ranged from 10−4 for lower concentrations and 10−5 for higher maltodextrin concentrations. The difference between the lower and higher concentrations lies on the rearrangements of macromolecules. Macromolecules do not need to rearrange or align at lower shear rates due to flow, but at stage 2, medium shear rates make molecules re-arrange, causing the shear thinning effect. Because the concentration of macromolecules is higher, the onset of the shear thinning effect occurs at smaller shear rates. The values of m are the cross exponent, which are m = (1 − n), where n is the power law flow behavior. Therefore, decreasing m values means that fluid is less shear-thinning and more Newtonian. Similarly to the power law model, flow behavior values are within the same range (0.8 to 0.7) for all concentrations and temperatures except when maltodextrin concentration is higher than 20%, where the flow falls for close to 0.5. Lira-Ortiz and co-workers found much lower values for the parameters of the cross model when analyzing the rheological properties of pectin from prickly pears. The smaller values might be due to the lower concentrations used[25].

      Thermodynamic analysis of avocado pulp flow behavior

    • Fluid flow is kinetically controlled, so an Arrhenius-type equation can determine the viscosity at any given temperature as long as the activation energy is determined. Equation 4 is thermodynamically derived and assumes the free volume theory, where an energy barrier exists for a molecule or a group of molecules, to move from one position to another, before and after flowing.

      Since Ea expresses the difficulty for a molecule to move from one position to another the intensity of molecular interactions, the bulkiness and rigidity of side groups are parameters that influence the Ea. Table 3 summarizes the activation energy of all samples. Values ranged between 5.96 to 12.93 kJ/mol depending on maltodextrin concentration. Shear rate used for calculation was 100 s−1 since it is considered as a typical value for pipe flow, agitation or swallowing[26]. Similar results were found for acai blueberry pulp, where increases in Brix resulted in higher activation energy[27]. The activation energy is the energy required to form a molecular cavity where to a given molecule 'jumps' leaving its temporary equilibrium position. The increases in the activation energy with maltodextrin concentration suggest that the hydrocolloid forms a new structure within the avocado pulp, hindering the mobility of molecules. The frequency factor is often associated with molecular collision, and the obtained values tend to decrease with increasing maltodextrin concentration. The explanation for such a result might be the molecular confinement and reduced mobility and, thus, reduction in the collision rate.

      Texture properties

    • We examined the effects of varying maltodextrin concentrations and temperatures on the textural properties of an avocado pulp. The textural parameters investigated include cohesiveness, consistency, firmness, and viscosity index and results are presented in Table 4.

      Table 4.  Instrumental texture analysis of avocado pulp samples with different maltodextrin concentrations at different temperatures.

      Maltodextrin
      concentration
      		Temperature
      (°C)      		CohesivenessConsistency
      (N)      		Firmness
      (N)      		Viscosity
      index (Pa·s)
      040.22 ± 0.017.81 ± 0.050.35 ± 0.020.47 ± 0.03
      0250.18 ± 0.016.97 ± 0.040.33 ± 0.020.31 ± 0.02
      0370.16 ± 0.015.69 ± 0.030.27 ± 0.010.17 ± 0.01
      5%40.22 ± 0.018.06 ± 0.050.36 ± 0.020.42 ± 0.03
      5%250.18 ± 0.017.52 ± 0.040.34 ± 0.020.37 ± 0.02
      5%370.17 ± 0.016.25 ± 0.030.29 ± 0.010.22 ± 0.01
      10%40.24 ± 0.018.14 ± 0.050.38 ± 0.020.44 ± 0.03
      10%250.19 ± 0.017.53 ± 0.040.35 ± 0.020.37 ± 0.02
      10%370.18 ± 0.017.29 ± 0.040.32 ± 0.010.27 ± 0.01
      20%40.32 ± 0.0210.72 ± 0.060.42 ± 0.020.79 ± 0.04
      20%250.19 ± 0.017.82 ± 0.040.35 ± 0.020.35 ± 0.02
      20%370.17 ± 0.016.94 ± 0.040.35 ± 0.020.19 ± 0.01
      40%40.34 ± 0.0212.09 ± 0.070.58 ± 0.030.99 ± 0.05
      40%250.28 ± 0.0211.72 ± 0.060.57 ± 0.030.76 ± 0.04
      40%370.23 ± 0.018.75 ± 0.050.42 ± 0.020.42 ± 0.02

      Cohesiveness, a measure of the internal binding forces within the food matrix, generally increased with maltodextrin concentration across all temperatures. This can be attributed to the fact that maltodextrin acts as a bulking agent and thickener, improving the overall structure and binding within the pulp. Additionally, cohesiveness was found to be highest at the lowest temperature (4 °C), which could be due to the increased viscosity at lower temperatures, leading to stronger interactions between the avocado pulp and maltodextrin particles.

      Consistency, an indicator of the thickness and flow behavior of the avocado pulp, also increased with maltodextrin concentration. This can be explained by the water-binding capacity of maltodextrin, which reduces the free water content and thus increases the thickness of the avocado pulp. The consistency was highest at 4 °C, followed by 25 °C, and then 37 °C. This trend can be attributed to the temperature-dependent behavior of the avocado pulp and maltodextrin-water interactions, where lower temperatures result in increased viscosity and reduced flow.

      Firmness, a measure of the force required to deform the avocado pulp, increased with maltodextrin concentration, consistent with the enhancement of the structural integrity of the avocado pulp due to the presence of maltodextrin. The firmness was highest at 4 °C, decreasing as temperature increased. This could be due to the avocado pulp's temperature sensitivity and the maltodextrin's water-binding capacity, which tends to weaken at higher temperatures.

      The viscosity index, which reflects the resistance of the avocado pulp to flow, increased with maltodextrin concentration, suggesting that the presence of maltodextrin increased the overall viscosity of the avocado pulp avocado pulp. The viscosity index was highest at 4°C, decreasing as the temperature increased. This is likely because viscosity generally decreases with increasing temperature as the components' molecular motion and kinetic energy increase, reducing the resistance to flow.

    Conclusions

    • In conclusion, this study comprehensively examined the rheological and textural properties of an avocado pulp with varying maltodextrin concentrations and temperatures. From a rheological perspective, our results highlighted that the avocado pulp exhibits non-Newtonian, shear-thinning behavior, with the Bingham, Ostwald-Waelle, and Cross models fitting the experimental data well. Maltodextrin concentration had a discernable influence on these properties, generally acting to reduce the initial flow barrier and serve as a lubricant at lower concentrations, while increasing yield stress and viscosity at higher concentrations. The thermodynamic analysis further reinforced these findings, demonstrating a direct relationship between maltodextrin concentration and activation energy, suggesting that maltodextrin forms a new structure within the avocado pulp that influences molecular mobility. Texturally, the avocado pulp's cohesiveness, consistency, firmness, and viscosity index increased with maltodextrin concentration, signifying the role of maltodextrin as a bulking agent and thickener. Furthermore, temperature pronounced affected both rheological and textural properties, with lower temperatures resulting in increased yield stress, viscosity, cohesiveness, consistency, and firmness. These findings have significant implications for the food industry, particularly when formulating fruit-based beverages with optimized sensory and rheological characteristics. By manipulating maltodextrin concentration and temperature, such beverages' flow behavior and texture can be tailored to suit specific consumer preferences and functional requirements. Further research would be beneficial to understand the behavior of other hydrocolloids and their interactions with fruit pulp in such systems, which would open up new avenues for innovation in the food and beverage industry.

    Author contributions

    • The authors confirm contribution to the paper as follows: investigation: Ribeiro S, Lima J, Batista L; formal analysis: Nascimento A; supervision: Almeida R; original draft preparation, review & editing: Lisboa H. All authors reviewed the results and approved the final version of the manuscript.

    Data availability

    • The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

      Conflict of interest

      • The authors declare that they have no conflict of interest.

      Rights and permissions
      • Copyright: © 2024 by the author(s). Published by Maximum Academic Press on behalf of Nanjing Agricultural University. This article is an open access article distributed under Creative Commons Attribution License (CC BY 4.0), visit https://creativecommons.org/licenses/by/4.0/.
    Figure (3)  Table (4) References (27)
  • About this article
    Cite this article
    Ribeiro S, Nascimento A, Lima J, Batista L, Almeida R, et al. 2024. Modulation of rheological and textural properties in avocado pulp: impact of maltodextrin concentration and temperature. Food Materials Research 4: e014 doi: 10.48130/fmr-0024-0005
    Ribeiro S, Nascimento A, Lima J, Batista L, Almeida R, et al. 2024. Modulation of rheological and textural properties in avocado pulp: impact of maltodextrin concentration and temperature. Food Materials Research 4: e014 doi: 10.48130/fmr-0024-0005
    shu

Catalog

  • HTML

  • Introduction
  • Materials and methods

  • Materials

  • Avocado pulp preparation

  • Rheological measurements

  • Texture analysis

  • Data modeling

  • Rheological models
  • Thermodynamic models for flow

  • Statistical analysis

  • Results and discussion

  • Rheological characterization of diluted avocado pulp

  • Bingham flow modeling

  • Ostwald-Waelle flow

  • Cross model

  • Thermodynamic analysis of avocado pulp flow behavior

  • Texture properties

  • Conclusions
  • Author contributions
  • Data availability
  • Conflict of interest
  • Rights and permissions
  • About this article
logo

Contents

Policies

Services

Partnerships

© 2025 Maximum Academic Press, except Open Access articles. MAP is a member of ALPSP, COPE, CrossRef, cOAlition S, OASPA and STM.

Privacy Policy  |  Site Map  |  Terms and Conditions

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return